Trajectory Design of Launch Vehicle with the Argument of Perigee Constraint for Highly Eccentric Orbit Mission

FENG Jihang ,ZHANG Weidong ,WANG Ying ,LIU Chang ,SHEN Zili

1 Shanghai Institute of Aerospace System Engineering,Shanghai 201109

2 Shanghai Academy of Spaceflight Technology,Shanghai 201109

Abstract:For the final stage of a launch vehicle which cannot start multiple times,the main constraint of a highly eccentric orbit launch mission is the argument of perigee,which is conditioned by the range.This paper studies the payload capacity at different launch sites for a highly eccentric orbit (e.g.GTO) and gives a method to improve the payload capacity with an argument of perigee constraint by increasing the sliding time before the final ignition and simultaneously adjusting the launch azimuth and yaw at the final stage.An example of launching to GTO orbit on a rocket from Hainan is given,which proves that the method has strong engineering value.

Key words:launch vehicle,highly eccentric orbit,constrain of argument of perigee,trajectory design

1 INTRODUCTION

The trajectory design of a launch vehicle is mainly based on the orbit requirements of a satellite and the overall technical state of the launch vehicle,as well as a reasonable selection of the flight attitude of the rocket,so that the launch vehicle flight meets the orbit requirements of the satellite,and at the same time payload capacity,landing point,overload and other limiting conditions have to be met.

The orbit parameters of a satellite can be determined by six standard parameters[1,2],which are semi-major axis,eccentricity,inclination,argument of perigee,right ascension of the ascending node and true anomaly.For satellites we generally use the mean element approach as the orbit design requirement.For trajectory optimization the mean element needs to be transformed to osculating orbit element in trajectory optimization.As the perigee height differs greatly from the apogee height in a highly-elliptical orbit,the altitude of the injection point of a launch vehicle varies greatly,which results in the great difference in the payload capacity.

Communications satellites and some navigation satellites at home and abroad operate in GEO orbits.Traditional launch plans are to launch satellites into GTO orbit (geosynchronous transfer orbit) where they will change their orbits at apogee and enter their predetermined orbits through phasing.At present,launch vehicles for launch missions to GTO,such as the Atlas V series of the United States,the Ariane series of Europe,the H-2A series of Japan,the LM-3 series and the LM-5 series of China,all meet the constraint requirements of GTO=180°),by starting the engine twice in the low temperature terminal stage when launching to GTO orbit.

This paper covers the research on the highly-elliptical orbit such as GTO orbit of the rocket on the assumption the engine cannot be started multiple times in the final stage,using a general core binding launch vehicle as an example to analyze the reason of payload capacity loss when sending a satellite into a highly-elliptical orbit under the constraint of argument of perigee.A trajectory design method for the final yaw maneuver is presented when the argument of perigee is not the optimal angle,and the appropriate slide and launch azimuth angle are adjusted before the final ignition,and it can meet the constraints of inclination and argument of perigee.This method can significantly improve the launch capability for a highly-elliptical orbit,especially GTO orbit.

2 MEAN ELEMENT TO OSCULATING ELEMENT

When the satellite separates from the launch vehicle,it must meet the satellite orbit parameters (denoted by mean elementLaunch vehicle trajectory design generally only considers J2 term short period perturbation and transforms orbit parameters intor,,ias a constraint function.The following calculation process of transforming from highly-elliptical orbit mean element into osculating element is under the condition only when considering J2 short period perturbation.

We define the trajectory parameters at the injection point(denoted by subscript f) asuf,rf,,if,φf.

Firstly,we transform mean elementinto osculating elementas,es,is,fs.The transformation steps are as follows[3,4]:

According to the osculating element,the requirement valueVa,ϑaandrat injection point is:

Then the constraint function is:

We can use sequential quadratic programming algorithm[5,6]to solve this question.

3 OPTIMAL ARGUMENT OF PERIGEE

For a launch vehicle with certain configuration and ellipse orbit with given inclination,perigee and apogee altitude,there is an optimal argument of perigee,which can provide maximum payload capacity.After a large number of simulation optimization calculations,without considering the ground measurement and control constraints,in most cases,the true anomaly of the orbit is near 0 degree or close to 360 degrees,can be found by using following iterative process as shown in Figure 1.

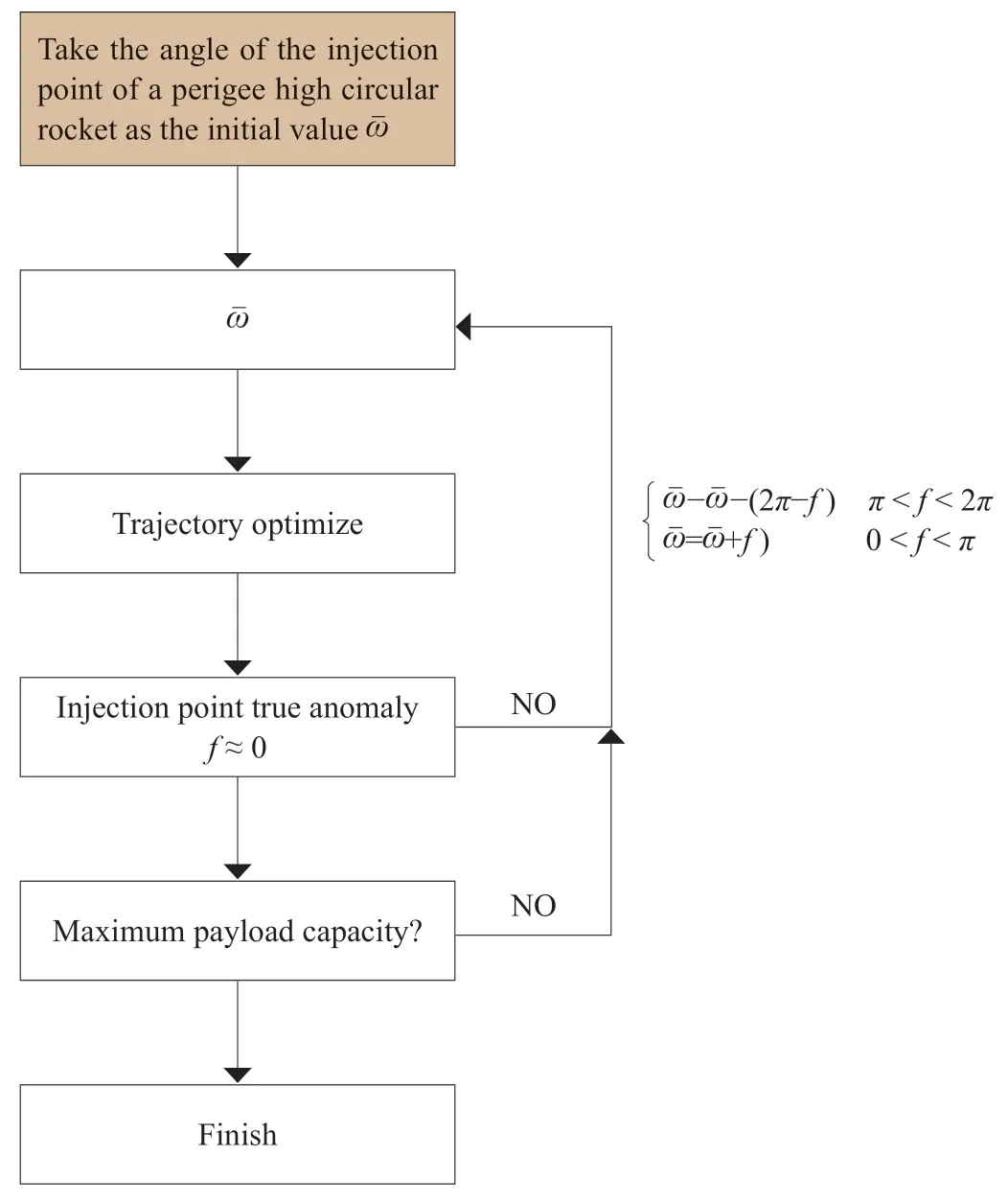
Figure 1 Iteration method for optimal argument of perigee

4 OPTIMAL ARGUMENT OF PERIGEE FROM DIFFERENT LAUNCHING SITES AND INCLINATIONS

This paper uses a general core binding launch vehicle as an example to analyze the trajectory design of southeast toward a highly-elliptical orbit from launch sites at Xichang and Hainan.

The launch vehicle is bundled with 4 general-purpose core stages in a two-and-a-half-stage configuration.The boosters and core stages are all liquid oxygen kerosene engines,and the second stage does not have the ability to start multiple times.We assume the perigee altitude of highly-elliptical orbit is 200 km and the apogee altitude is 35786 km.

According to the calculation method of optimal perigee argument in the last section,by optimizing the optimal perigee argument of this elliptical orbit from Xichang and Hainan and calculating the payload capacity under different orbit inclinations and perigee arguments,the results are shown in Figure 2.

Figure 2 Launch capacity with different arguments of perigee and inclinations

It can be seen from Figure 2 that under the condition of a no power phase yaw maneuver,the conclusions are as follows:

a) For the same launch site and same orbit inclination withdiverging from the optimal,the payload capability decreases greatly;

b) For the same launch site but different orbit inclinations,the optimal perigee argument is different and the larger the orbit inclination,the larger the optimal perigee argument;

c) For different launch sites but the same orbit inclination,the optimal perigee argument is different and the lower the latitude of launch site,the larger the optimal perigee argument.

5 ANALYSIS OF PAYLOAD CAPACITY DECREASE

From Figure 2 it can be seen that with the deviation offrom the optimal value,the payload capacity will significantly decrease.According to the trajectory optimized result,from Figure 3 we can see that under differentconstraints,the launch vehicle injection points are almost at the same longitude and latitude.As the angle between perigee and injection point is differs,the altitude of injection point is different.From the flight altitude curve in Figure 4 we can see that because of the limitation of the power phase of the voyage,whenincreases,the active stage of the launch vehicle has to raise the trajectory,which increases the height of the rocket’s injection point and increases the gravity loss,resulting in a significant drop in the payload capacity.Therefore,reducing the angle between the rocket’s injection point and the perigee is the key to improve the launch capability to highly-elliptical orbits.

Figure 3 Injection point with different arguments of perigee

Figure 4 Flight altitude with different arguments of perigee

6 TREATMENTS WHEN IS NOT OPTIMAL

In traditional launch vehicle trajectory design,if the satellite orbital inclination is greater than the geographic latitude of the launch site,there is no need to perform active yaw maneuvers without adjusting the rocket landing points,because this will lose part of the payload capacity[7,8].However,according to the analysis mentioned above,when the orbit is highly-elliptical and the constraint value ofis larger than optimal,the attempt of increasing the slide time before the final stage ignition,adjusting the launch azimuth and increasing the yaw maneuver at the last stage,is possible to meet the orbit inclination requirement and reduce the decrease of payload capacity caused byconstraint at the same time.

Firstly,we try to increase the slide time before final stage ignition when theis greater than the optimal.After trajectory optimization,it is found that with the increase of the secondary slide time,the payload capacity is greatly improved compared to the direct launch.

Secondly,we increase the launch azimuth angle and the second-level yaw maneuver to optimize the payload capacity under differentAfter trajectory optimization,it was found that as the argument of perigee increases,the payload capacity improves more than simply increasing the secondary slide time,thus further improves the payload capacity.

It can be seen from Figure 5 that the general core binding launch vehicle without yaw maneuver has an optimal perigee argument of 130° at this inclination and the corresponding payload capacity is 6242 kg.When=180°,the payload capacity is 0 kg,not have the ability to directly launch to GTO orbit.

Simply increase the slide time before the secondary ignition,the GTO payload capacity will be increased from 0 kg to 2200 kg.This method is only applicable when theis greater than the optimal argument of perigee.

The GTO payload capacity of the purely final stage yaw maneuver mode is increased from 0 kg to 3700 kg.This method is not only suitable for the case where theis greater than the optimal argument of perigee,but also for the case where theis less than the optimal argument of perigee.When using this method,you need to consider the safety of the landing points .

Figure 5 Comparison chart of payload capacity under three methods

Taking the launch to GTO orbit from Hainan=180°,Hp=200 km,Ha=35786 km) as an example,the relevant trajectory results under two design methods are given.Table 1 shows the comparison of the parameters of the GTO orbit launch injection point under the two improved methods.Figure 6 and 7 show the comparison of the rocket trajectory and related trajectory parameters.

It can be seen from the flight path in Figure 6 that the angle between injection point and perigee under second stage yawing condition is far less than unyawed condition and the drop of in-jection point altitude is the root cause of the payload capacity decrease.The contrast of injection point parameters under two launch modes are listed in Table 1.The yawing condition would change the injection point of the rocket,meanwhile the orbit ascending node longitude changed which leads to a smaller injection point true anomaly.However,satellites generally only have the requirement of right ascension of ascending node,and this can be realized by changing the launch window.

Table 1 Osculating orbit element of launch vehicle injection point

Figure 6 Trajectory contrast

Figure 7 Trajectory parameter contrast

From the above analysis,it is possible to combine the above two methods to further increase the payload capacity into GTO orbit.We optimized the GTO payload capacity by increasing the rocket launch azimuth while increasing the slide time of the second stage.After trajectory optimization,the GTO payload capacity was increased to 5200 kg by this method.Compared with the single yaw maneuver mode,the payload capacity was increased by 1500 kg,and the rocket landing points were all located on the high seas of the Pacific Ocean,meeting the safety requirements.

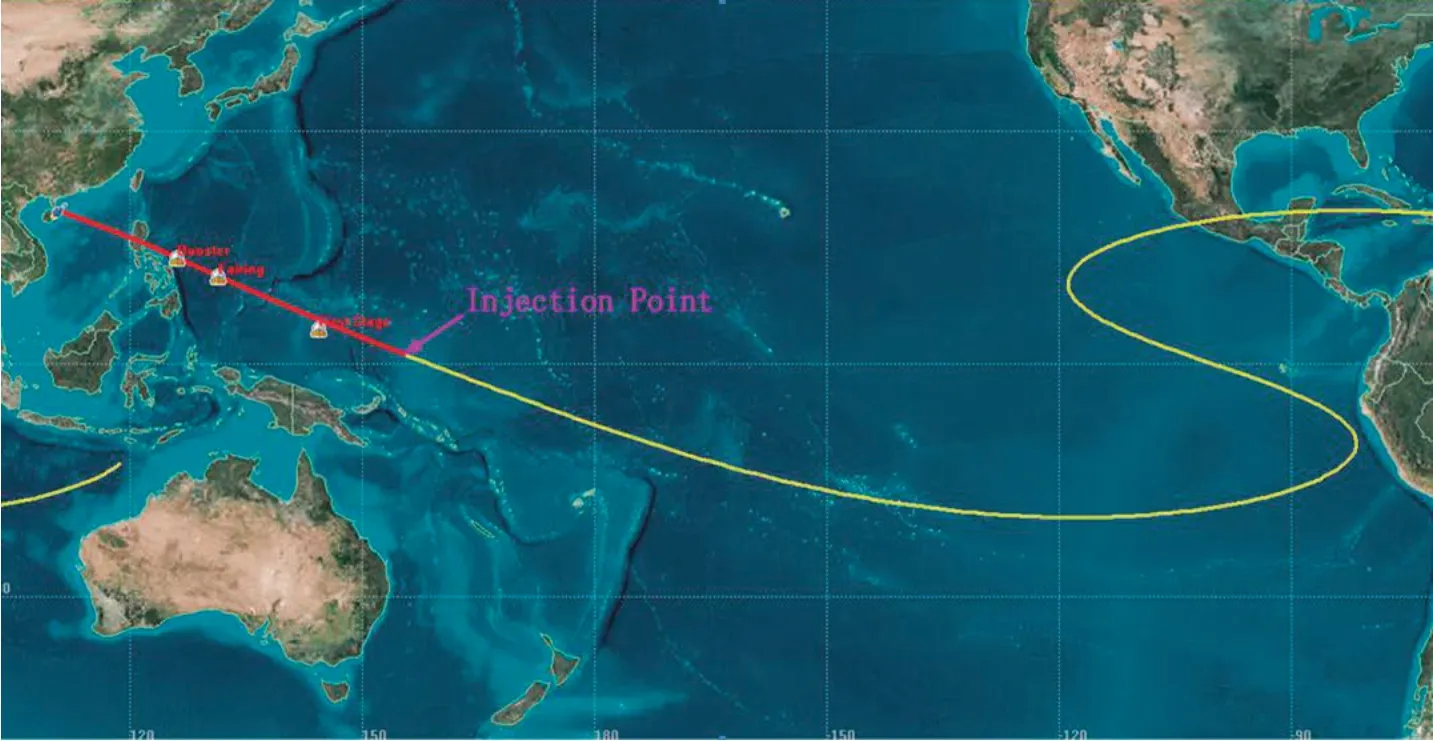
Figure 8 Trajectory graph

Figure 9 Trajectory parameter

From the comparison between Figure 9 and Figure 7,it can be seen that the sliding and yaw maneuver method used to launch to the GTO orbit,the sliding time and yaw angle are smaller than the single sliding and yaw maneuver method,so the payload capacity can be further improved.

7 CONCLUSION

This paper analyzes in detail about the trajectory design of a launch vehicle for highly-elliptical orbit launch mission and proposes a way of calculating the optimalIt was found by theoretical analysis and simulation that the optimal argument of perigee is closely related to the launch point,direction and range of the rocket.

A launch vehicle whose final stage does not have multiple ignitions would significantly lose payload capacity with the increasing of perigee argument required value.In traditional rocket trajectory design,sliding before the final stage ignition and yaw maneuvers in the active section will greatly reduce the payload capacity.However,when the highly-elliptical orbitconstraint is strong,enabling proper sliding and adjustment of the launch azimuth before the final stage is ignited,and with an increase in the yaw maneuver in the active section of the rocket,this can greatly improve the payload capacity.

In view of the launch to GTO from Hainan,the adjustment of the launching azimuth has little effect on the safety of landing points.Therefore,the method proposed in this paper is of great engineering significance for GTO orbital launch missions from Hainan using a launch vehicle whose final stage does not have multiple ignitions.