基于混沌进化的引力搜索频谱调度算法

王亚利 于继明

1(济源职业技术学院 河南 济源 454650)2(金陵科技学院 江苏 南京 211169)

0 引 言

随着无线通线技术的快速发展，涌现出越来越多针对不同应用场景的无线通信设备，例如应用于移动健康监测的可穿戴设备[1]、应用于共享经济的共享单车，以及应用于智慧交通的车载网络[2]等。但无线设备数量增长给不可再生的频谱资源带来了巨大的压力，从而不可避免地会加剧数据丢包、时延、信道拥塞等状况。另一方面，这些无线设备通常使用的是政府授权的商业频谱，例如无线通信运营商的频谱；或特别准许工业界、科学界和医疗界所使用的公共频谱，例如Wi-Fi、蓝牙等所使用的频谱[3]。文献[4]显示，除上述两类频谱，其他授权频谱的使用率非常之低，最低仅有15%。综上，面对频谱资源使用率冰火两重天的状况，认知无线电[5](Cognitive Radio，CR)技术应运而生。

CR技术的主要特点是可以帮助无线设备在不影响其他用户的前提下使用授权频谱进行通信，以提升无线通信质量，同时提升频谱利用率[6]。配备CR技术的无线设备所组成的网络称为认知无线电网络[7](Cognitive Radio Networks，CRNs)，其中包括若干个授权用户(Authorized User, AU)，以及若干个非授权用户，可以称之为认知用户(Cognitive User, CU)。在CRNs中，最关键的问题是如何将有限的授权频谱资源以一种合适的方式分配给认知用户CU，在不影响授权用户AU正常使用的前提下，保证认知用户CU之间使用频谱的公平性，即在一个成熟的系统模型中设计一套完善的调度算法对授权频谱资源进行管理。

目前已有许多学者提出了不同的频谱调度系统模型。干扰温度频谱调度模型[8]的出发点是通过设定一个温度门限值对认知用户CU的传输功率进行控制，以确保其不会对授权用户AU造成干扰，但该模型忽略了授权频道复用的可能性。博弈论频谱调度模型[9]不同于干扰温度模型，其出发点是实现系统的最大效用，降低系统的使用成本，让认知用户CU之间进行博弈，确定最优的频谱调度策略，但该模型却忽略了用户之间的公平性。图论频谱调度模型[10]的思想是将一个实际的问题转化为一个数学模型，具备较强适用性，能够根据问题的特点在数学模型中有效地体现，避免干扰温度模型和博弈论模型中出现的问题。

基于图论模型所设计的频谱调度问题是一个NP-Hard问题，所以研究学者利用智能寻优算法进行求解。文献[11]利用遗传算法求解频谱调度问题的最优方案，最然具有一定的全局搜索能力和较高的适应性，但是算法的性能却依赖初值的选择，且算法后期易陷入局部最优。文献[12]利用蚁群算法优化频谱调度方案，其具备较高的算法收敛精度和全局搜索能力，但收敛速度较慢。引力搜索算法[13](Gravitational Search Algorithm, GSA)相比于遗传算法和蚁群算法是一种新兴的群体智能寻优算法，其能够解决较高维度的空间优化问题，且对初始值不敏感，种群能够维持较高的多样性。但引力搜索算法依然面临一些问题，其收敛速度和收敛精度仍有提升的空间。

通过以上对频谱调度系统模型和智能寻优算法两方面的分析，本文在图论模型的基础上，以系统效用最大化为优化目标，提出一种基于混沌进化的引力搜索算法(Chaotic and Evolutional Gravitational Search Algorithm, CEGSA)以求解认知无线电网络中的频谱调度问题。在CEGSA中，基于所构建的系统模型，本文在算法的迭代阶段引入差分进化[14]过程，以加快算法的搜索速度，提升CEGSA的收敛速度，并引入混沌扰动机制[15]，避免算法在后期陷入局部最优解，以提高CEGSA的算法精度。

1 系统模型及优化问题

1.1 CRN模型

相比于干扰温度模型和博弈论模型，图论模型可以表征用户之间的关系，以及更直观地展现网络中的拓扑结构。具体地，本文基于图论理论所构建的CRN模型可以展示出不同节点(即用户)之间的干扰关系，并通过对节点之间的连接线进行着色，用以表示用户之间的冲突。同时，节点的干扰半径由用户的干扰范围所决定。而对于目标函数，CRN模型有较好的泛化能力，可以根据不同的优化需求设计目标参数。

综上，基于图论理论，首先构建了一个图论模型G=(V,E)，其中:V代表图的节点，在CRN模型中表示授权用户AU和认知用户CU；E代表图的边，在CRN模型中表示用户之间的干扰关系，包括AU和CU之间，以及CU和CU之间的干扰关系。图1所示为一个CRN模型图，包含3个AU、4个CU，以及3个可用授权频谱K∈{α,β,δ}，其中：r1表示AU的干扰半径，r2表示CU的干扰半径，如果干扰区域相互重叠，则表示它们在使用同一频谱时会发生干扰。

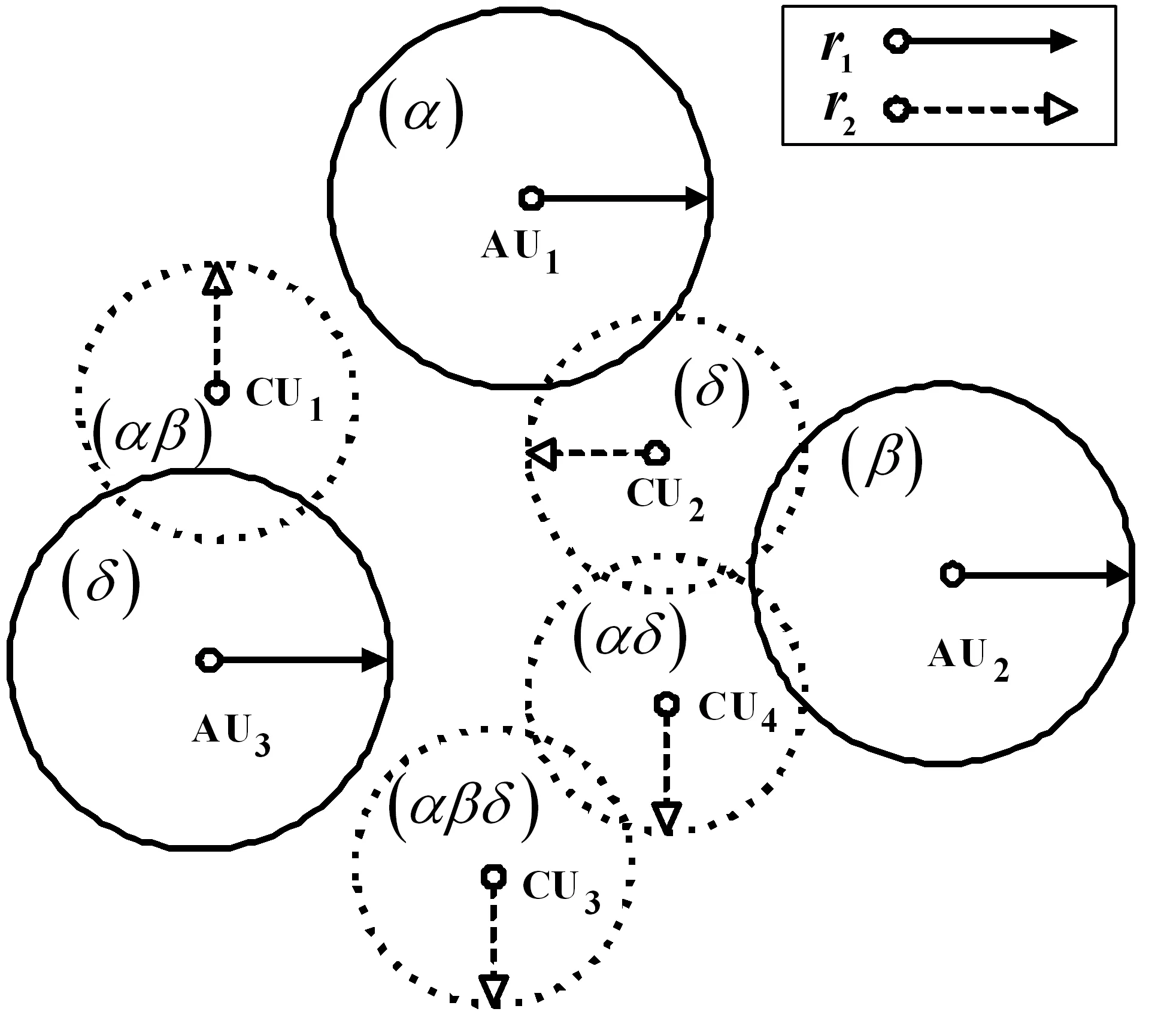
图1 CRN系统模型

1.2 矩阵模型

频谱调度算法有三个设计原则，分别是：较高的算法执行效率，体现网络中的约束，明确的优化目标。而1.1节所构建CRN模型并不能直接用数学方法进行求解，所以，本节将其拓扑结构以及用户之间的干扰关系转换为矩阵模型。

首先，本文设计拓扑矩阵T和效用矩阵E用以表示CRN网络的拓扑结构和节点的权重，其可以将图形化语言转化为数学语言，方便使用计算机设计算法求解。然后，本文设计干扰矩阵I表示网络的约束条件，用于确保所设计的算法在执行过程中满足网络中用户的干扰关系。最后，本文设计位置矩阵P和共享矩阵S作为算法的输入和输出，其中输出矩阵S则是本文的优化目标。具体地，定义认知用户CU的个数为N，无线频谱的个数为K，且 1≤n,m≤N，1≤k≤K，具体见表1。

表1 矩阵模型

(1)拓扑矩阵T：定义了网络空间中用户的拓扑结构tn,k=1。具体地，可以从拓扑矩阵T中确定认知用户n是否可以使用信道K，即表示可用，否则反之。例如:从图1中可得，用户CU2与AU3的干扰范围没有交集，则t2,3=1。

(2)效用矩阵E：定义了用户n使用频谱K时的效用。该效用由当时的网络环境参数所决定，例如信噪比、传输功率，具有较强的动态性。

(3)干扰矩阵I：定义了AU与CU以及CU与CU之间干扰关系的三维矩阵。当n≠m时，in,m,k=1表示CUn和CUm同时使用频谱k时有干扰，否则反之；当n=m时，in,m,k=1表示CUn使用频谱k会对授权用户产生干扰，否则反之。例如：从图1中可得，i1,3,α=0，i2,4,δ=1。

(4)共享矩阵S：定义了最终的频谱调度方案，sn,k=1表示将频谱k分配给CUn使用，否则反之。此外，矩阵S需要满足干扰矩阵I的要求，即当in,m,k=1且n≠m时，必须满足sn,k+sm,k≤1。

(5)位置矩阵P：为方便计算机处理，本文设计了一个编码解码过程，将拓扑矩阵T编码为物体的位置向量P，通过GSA一系列的运算，并将最后得到的最优解P解码为共享矩阵S。编码解码的核心是将拓扑矩阵中1元素的位置按照先行后列的顺序按次取出，并组成一个行向量，最后再按照该规则还原至共享矩阵S，如图2所示。定义位置矩阵P表示空间中所有物体的位置向量集合，其中：μ表示空间中物体的个数；ε表示物体位置的维度，其值等于拓扑矩阵T中1元素的个数。

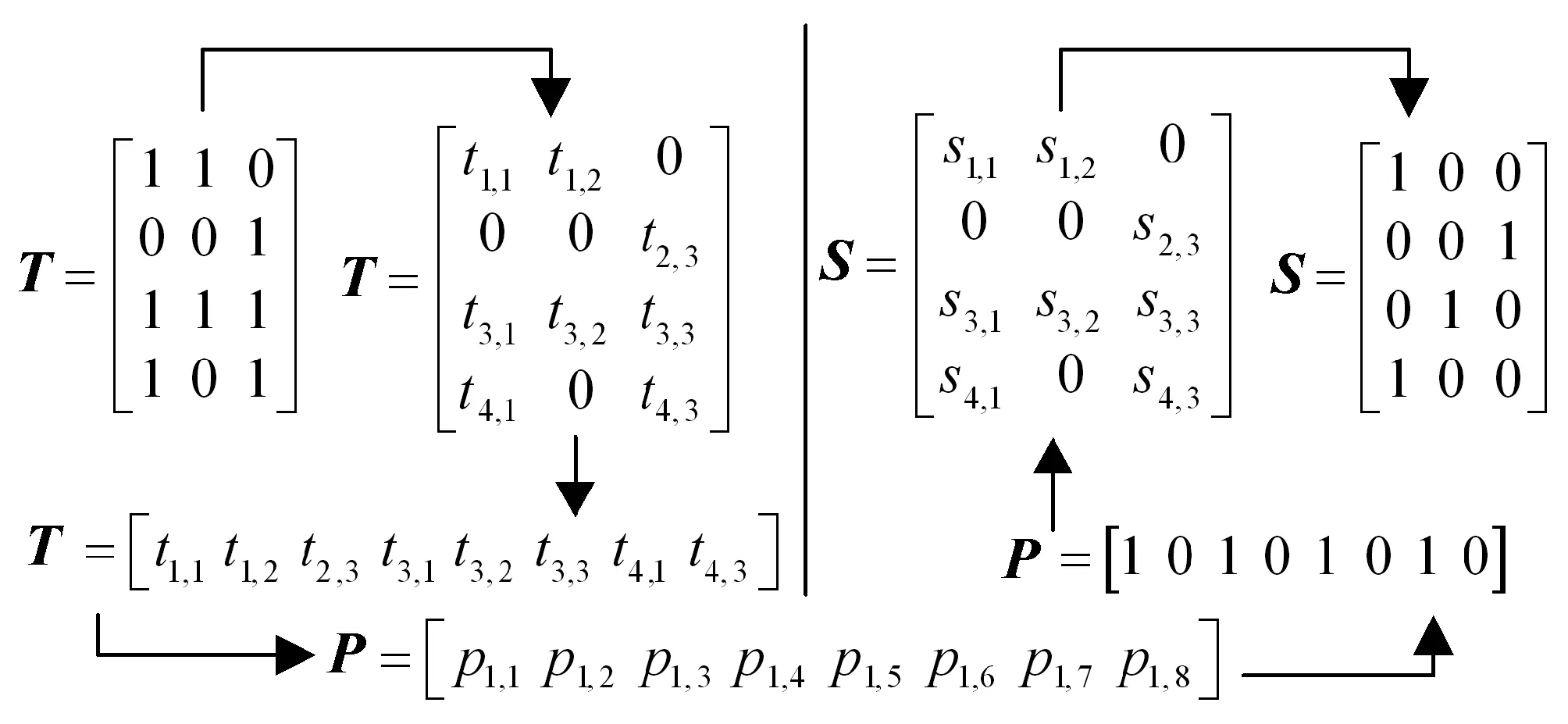
图2 位置矩阵P编码解码

1.3 优化问题

定义物体位置的适应度函数，用于评价物体位置的优劣：

(1)

本文的优化问题是最大化CRN的系统效用，即在满足干扰矩阵I的约束条件下，将最终的频谱分配方案矩阵S乘以系统的效用矩阵E。

s.t. ∀1≤n,m≤N,1≤k≤K

(2)

2 算法设计

2.1 算法优化思想

引力搜索算法GSA[13]模拟了宇宙中任意两个物体之间都存在相互作用力的特性，利用万有引力公式，将优化问题转化为宇宙中物体的位置，并由物体的质量和物体间的距离计算引力的值，最后根据引力值推演物体下一次运动的方向和距离。通过不断的移动，物体会聚集到质量最大的物体附近，而物体的质量由评价函数确定，即质量最大的物体占据着最优的空间位置。这样，GSA通过万有引力定律将优化问题的评价函数以及解映射到了空间中物体的位置和质量。GSA相比于遗传算法和蚁群算法具有天然的优势，例如对初始值不敏感、具有较高的个体多样性等，但GSA由于万有引力定律的性质仍然面临一些问题，例如后期容易陷入局部最优，且收敛速度仍有提高的空间。基于此，本文分别设计了差分进化优化(Differential Evolution Optimization,DEO)机制和混沌扰动优化(Chaos Disturbance Optimization,CDO)机制来解决上述两个问题，并同时提高了GSA的收敛速度和收敛精度。

2.2 差分进化优化机制

2.1节介绍了GSA的核心思想，即物体基于万有引力定律向所有质量比自己大的物体的合力方向运动。在这样的机制下，受影响最大的是空间中质量最小的物体，反而质量最大的物体可能会纹丝不动，不进行任何搜索。所以算法的收敛速度取决于质量偏小的物体，因其运动更敏捷，搜索范围更自由。

基于此，本文设计了差分进化(DEO)机制对GSA的搜索过程进行优化，主要从三方面做了算法适配和优化工作：(1)该机制在GSA每次迭代完进行，且仅针对质量最小的部分物体；(2)DEO机制中的变异操作，仅针对质量最大的部分物体；(3)设计了随机变异位，以确保每次操作至少在一维会有改变。综上，本文设计的差分进化公式为：

(3)

式中：t表示位置的迭代次数，且1≤t≤T；φ为区间(0,1)之间的随机数；ρ为选择概率；λ为缩放因子；εrd为位置p的任意一个维度，每次迭代随机产生，且1≤εrd≤ε；μ1、μ2、μ3为三个随机选择物体，且满足μ≠μ1≠μ2≠μ3。

假设物体μ经过GSA优化后的位置向量为P=(A，B,C, …)，εrd设为3，则DEO机制的交叉过程如图3所示。

图3 差分进化过程

基于式(3)，假设ε=1时，φ≤ρ，则将A2替换为A；假设ε=2时，φ>ρ，则将B1替换为B；由于εrd=3，所以强制将C2替换为C；之后的交叉位选择也依据式(3)进行操作。

综上，基于DEO机制优化后的GSA，可以增强大质量物体对小质量物体搜索路径的引导，即通过调节选择概率ρ，GSA就可以调整小质量物体的进化速度，在保留一部分原有物体的位置因素的情况下，基于大质量物体的引力方向，对其下一个时隙的运动位置进行调整。对部分大质量物体的变异操作则增强了物体种群的多样性，避免空间中的物体迅速聚拢在部分大质量物体周围，陷入局部最优。变异位εrd则可以在小质量物体向大质量物体聚拢的过程中，对其运行轨迹触发小范围的波动，使其在不影响小质量物体的整体运动趋势下，增加发现其他最优区域的可能性，提升算法的寻优速度。

2.3 混沌扰动优化机制

GSA的另一个特性是，在算法迭代的后期，所有的物体都会向质量最大的物体靠近，这会导致算法易陷入局部最优。为了避免这种问题，帮助算法找到全局最优解，提升算法精度，本文设计了混沌扰动优化(CDO)机制。该机制利用了混沌映射产生的随机点可以遍历整个空间且不重复的特性，在GSA经过多次迭代，但最大物体质量不变的情况下，对空间中的所有物体进行扰动，打乱其所在的位置。本文所使用的混沌映射为Tent映射：

(4)

其混沌扰动的步骤如下：

1)将物体μ的位置Pμ映射到混沌扰动空间[0,1]：

(5)

(6)

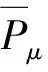
2.4 算法流程

本文所提出的CEGSA流程如下：

1)初始化位置矩阵P。根据式(1)计算每个物体的适应度，记最大适应度为Rb，其位置向量记为Pb。

2)计算物体质量。根据上文建立的物体质量与适应度函数之间的联系，定义物体μ在第t代的质量为Mμ(t)：

(7)

(8)

式中：Rb(t)和Rw(t)分别表示第t代所有物体中最大和最小的适应度；μ和υ表示不同的物体。

3)计算物体所受引力之和。首先计算物体υ对物体μ的引力，Dμ,υ为物体μ和υ之间的欧氏距离；G(t)为动态引力常数，随迭代次数而减少；此外，G0是G(t)的初值，σ是无穷小量，ζ是引力系数。

(9)

Dμ,υ(t)=‖Pυ(t),Pμ(t)‖2

(10)

(11)

则物体μ所受的合力为：

(12)

4)计算物体加速度。由式(8)和式(12)，便可以得到物体μ在t代的加速度：

(13)

5)更新物体速度和位置。分别计算物体在t+1代的速度和位置，所有物体初始化速度为0。

Vμ(t+1)=Vμ(t)+aμ(t)

(14)

Pμ(t+1)=Pμ(t)+Vμ(t+1)

(15)

6)差分进化优化物体位置。由EDO机制对空间中的物体进行优化，优化的数量定为μEDO。

7)更新物体的最大适应度。由式(1)计算所有物体的适应度，并将第t代最大适应度Rb(t)与Rb进行比较，保留最大值，更新至Rb、Pb。

8)判断是否进行混沌扰动。定义进行混沌扰动的阈值为TCDO，即当空间中最大的物体质量连续TCDO代都没有改变，则由CDO机制对空间中的物质进行扰动。

9)判断是否到达最大迭代次数，否则转步骤2)。

3 实 验

本文基于MATLAB平台构建了CRN网络模型，并在该平台中设计基于混沌进化的引力搜索算法以求解认知无线电网络中的频谱调度问题。模型所产生的网络的拓扑结构由文献[17]得，仿真环境为20×20的方形区域，包括K个AU、μ个CU、K个授权频谱。另外，授权用户AU和认知用户CU的干扰半径分别定为r1=5，r2=3。

本文分别从收敛速度和收敛精度两方面对CEGSA、GA[11]、GSA[13]进行了对比实验。为了确保仿真结果具有可比性，三个算法的种群个数均设为20，迭代次数设为T=200。其他参数设置如下：GA的变异概率设置为0.2，交叉概率为0.7，GSA和CEGSA的G(t)初始值G0=100，引力系数ζ=20，CEGSA的其他参数μEDO=6，TCDO=3。

此外，收敛速度实验为300次实验的均值，收敛精度实验为30次实验的均值，且每次实验都会生成新的网络拓扑结构。

3.1 收敛速度实验

如图4所示，本文在K=5、μ=15的网络环境下对CEGSA、GSA和GA进行实验，比较其收敛速度。

图4 收敛速度实验

可以看出，CEGSA的收敛速度最快，在62代附近收敛；GSA次之，在85代附近收敛；GA最慢，在110代附近收敛。这是因为GSA在多维空间具备较高的搜索性能，且CEGSA利用差分进化机制对空间中质量较小的物体进行了优化，验证了DEO机制的有效性。此外，表2总结了三个算法收敛时的系统效益，以及相对于GA的效用提升比例。可以看到CEGSA的系统效用要高于其他两种算法，验证了混沌扰动机制对系统效用的提升起到一定作用。

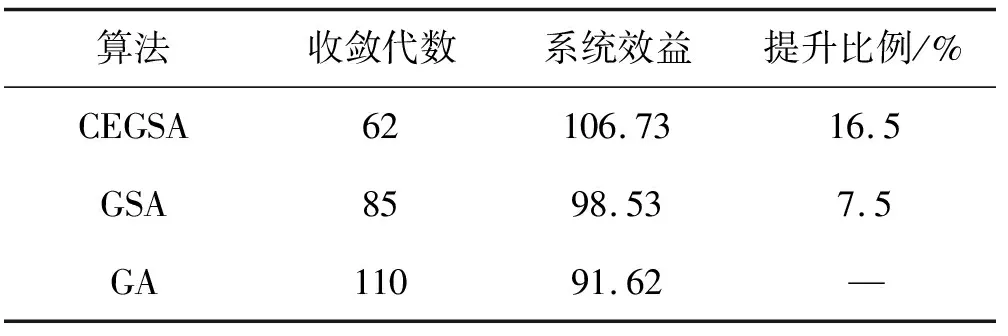
表2 算法收敛性能

3.2 收敛精度实验

本文对三种算法的收敛精度进行对比实验。图5为频谱个数K=7固定，认知用户CU个数μ从3递增至21时系统效用的变化。图6为μ=15固定，频谱个数K从3递增至19时系统效用的变化。

图5 收敛精度实验1

图6 收敛精度实验2

从图5可以看出，三种算法的系统效用随CU数量的增加而增加，在认知用户数μ>15后趋于缓和。这是由于频谱个数固定，即使CU不断增加，也无法满足所有的CU都有频谱资源可以用，所以系统效用趋于峰值。此外，也可以看到CEGSA的系统效用一直高于其他两种算法，在此证明本文所提出的CDO机制对GSA的收敛精度具有一定提升。

从图6可以看出，三种算法的系统效用随频谱个数的增加而增加，且CEGSA仍然高于其他两种算法。此外，可以看到K>7之后，三种算法的差距越来越大，这是由于K≤7时，频谱资源紧张，无法体现出各个算法的性能。同时，可以看到三个算法在K>15后系统效用R(t)上升放缓，这是由于CU个数是固定的，频谱资源增加并不会提升系统的效益。

4 结 语

本文针对传统频谱调度算法所面临的问题，从算法的收敛速度和收敛精度两方面进行考虑，以最大化系统效用为目标，提出了基于混沌进化的引力搜索频谱调度算法。设计了差分进化优化机制，对传统引力搜索算法中物体移动轨迹进行指导，加快算法的寻优过程，并利用变异过程提升了种群的多样性；设计了混沌扰动优化机制，当算法陷入局部最优时，利用混沌算法特性对空间中的物体进行扰动，以提高算法的精度。实验结果表明，本文算法相比于传统引力搜索算法和遗传算法有更高的收敛速度和系统效用。