ARIMA 模型和ARIMA-SVM 模型对上海市2 型糖尿病患者肺结核发病的预测效果

黄国宝 黎衍云 吴 菲 沈 鑫 徐望红

（1复旦大学公共卫生学院流行病学教研室 上海 200032；2上海市疾病预防控制中心 上海 200336）

2 型糖尿病（type 2 diabetes mellitus，T2DM）和结核病（tuberculosis，TB）是常见的慢性病，两者高发年龄吻合，且相互影响。TB 又以肺结核（pulmonary tuberculosis，PTB）最为常见。流行病学调查发现，T2DM 患者发生结核病的概率是非T2DM 患者的2～3 倍，且与地区、种族无关［1-2］。我国首次糖尿病-结核病双向筛查结果显示，糖尿病患者TB 检出率为1.25%，远高于非糖尿病患者的0.36%。而TB 患者若合并糖尿病，则病程进展更快、疗效差、耐药率高、预后凶险。上海市嘉定区2008—2014 年的一项调查显示，PTB 合并糖尿病的患者中，痰涂片阳性、合并空洞、治疗失败和转入耐多药和复治患者占比分别达73.67%、56.32%、4.21%和13.16%，远高于未合并糖尿病患者的42.51%、52.91%、0.14%和7.02%［3］。鉴于T2DM 患者的TB 发病率高于一般人群，且两病共患患者预后较差，及时掌握T2DM 人群中TB 发病情况，将有利于结核病防控和糖尿病管理。

差分自回归移动平均（autoregressive integrated moving average，ARIMA）模型是预测疾病发病率较为成熟的建模方法，常用于预测PTB、HIV、乙肝等传染病的发病率［4-5］。中国是T2DM 与TB 同时高发的国家，T2DM 合并TB 的患者逐年增加。“十三五”全国结核病防治规划倡导在糖尿病患者等重点人群中开展TB 的主动筛查。因此，急需在数量庞大的中国T2DM 患者中建立TB 预测模型，以预测相关疾病负担，制定和评估有针对性的防控策略和措施。

本研究以上海市2010—2015 年T2DM 患者管理数据和结核发病监测数据为基础，选择时间序列模型中的ARIMA 模型，并用支持向量机（support vector machine，SVM）对残差进行拟合，建立结核病发病率的组合预测模型，对T2DM 患者的PTB 发病率进行预测。

资料和方法

资料来源资料来自2010—2015 年上海市糖尿病管理系统和结核监测系统数据库。研究对象纳入标准为：（1）上海市户籍；（2）糖尿病诊断时间为2010—2015 年；（3）糖尿病确诊时年龄≥35 岁；（4）确诊时未患PTB 或已治愈。共纳入T2DM 病例217 999 例。将T2DM 病例的身份证号与上海市结核监测系统进行链接，获得PTB 发病信息。在纳入上海市糖尿病管理系统和结核病监测系统时，所有研究对象已口头知情同意所录入系统信息的分析使用。

ARIMA 模型时间序列分析的基本思想是将预测对象随时间变化而形成的序列看作一个随机序列，除偶然原因出现的极个别序列值外，时间序列是依赖于时间（t）变化的一组随机变量，可以利用该序列的过去值、现在值来预测序列的未来发展状态［6］。ARIMA 模型由Box 和Jenkins 提出，也叫博克斯-詹金斯（简称B-J）法，在ARIMA 模型中预测值表达式为过去若干个取值和随机误差的线性函数［7］。其基本结构为不包含季节性的ARIMA（p，d，q）和包含季节性的ARIMA（p，d，q）（P，D，Q）。模型建立的步骤如下［8］：

模型识别 通过时序图及单位根检验判断序列平稳性。非平稳的序列一般可以通过差分转换为平稳序列，根据差分的次数来确定差分（d）和季节差分（D）。

模型拟合及参数估计 根据序列自相关函数（autocorrelation function，ACF）和偏自相关函数（partial autocorrelation function，PACF）分析图［9］，判断模型自回归阶数（p）、滑动平均阶数（q）、季节回归阶数（P）以及季节滑动平均阶数（Q）。

模型检验 即对模型的残差进行白噪声检验：若白噪声检验结果P＜0.05，则需回到上一步骤，重新进行参数估计，拟合新的模型。若白噪声检验结果P＞0.05，说明序列信息已经提取完整，模型结果合适，但仍需重新进行上一步骤，拟合新的模型。若同时有几个模型残差序列通过白噪声检验，且参数检验结果有意义。则根据拟合优度统计量标准化贝叶斯判别准则（standardized bayesian information criteria，SBIC）和赤池信息（Akaike information criterion，AIC）最小的原则选择最优模型。

支持向量机SVM 是Corinna Cortes 和Vapnik等于1995 年提出的一种机器学习方法，主要用于非线性回归领域。它能够更好地解决小样本集模型难以选择、经验风险原则的样本容量依赖、维数灾难、过拟合而外推差、局部极小点等问题［10］。

ARIMA-SVM 组合预测步骤将一组时间序列的数据Yt看成由线性结构Lt和非线性结构Nt组成，即Yt=Lt+Nt。。运用ARIMA 模型拟合时间序列的线性结构，SVM 拟合时间序列的非线性结构。ARIMA-SVM 具体建模步骤见图1。

图1 ARIMA-SVM 的组合预测模型流程图Fig 1 Flow chart of ARIMA-SVM hybrid model establishment

模型的拟合和预测效果评估模型的评估分为内部数据评估（模型拟合程度评估）和外部数据评估（预测效果评估）。ARIMA 和ARIMA-SVM组合模型的预测效果采用近期预测法，基于2015 年1 月—12 月PTB 月发病率数据进行。为了考察模型预测效果，用平均绝对百分误差（mean absolute percentage error，MAPE）和均方根误差（root mean square error，RMSE）来测定模型预测的精度。MAPE 和RMSE 越小，预测精度越高。

统计学分析运用SPSS 23.0 统计软件建立和整理发病资料数据库，利用相关统计学模块进行数据处理和分析，实现ARMIA 建模过程。对ARIMA模型拟合值与真实值的残差序列进行样本重构获得SVM 样本集，使用R 3.6.2 中的e1071 包对残差进行SVM 预测。tune.svm（）函数确定核函数的参数，使用svm（）函数拟合模型。

结果

ARIMA 模型的建立ARIMA 模型建立使用2010 年1 月—2014 年12 月上海市户籍T2DM 患者PTB 月发病率，绘制时间序列图，并对其趋势性、季节性和随机误差进行分解。由结果可知，该序列是一组包含季节和趋势的非平稳队列，初步确定模型结构为ARIMA（p，d，q）（P，D，Q）12（图2、3）。

图2 上海市2010—2014 年T2DM 患者PTB 发病率时序图Fig 2 Time series plot of PTB incidence in T2DM patients in Shanghai from 2010 to 2014

图3 上海市2010—2014 年T2DM 患者PTB发病率时间序列分解图Fig 3 Decomposed time series plot of PTB incidence in T2DM patients in Shanghai from 2010 to 2014

模型识别对序列进行1 阶逐期差分和12 阶季节差分后，时序图及单位根检验（augmented dickey fuller，ADF）结果显示，差分后序列呈稳定序列（t=-5.789 8，P＜0.01），判断d=1，D=1。为了判断模型p、q、P 和Q 值，需要绘制差分处理后的ACF 图和PACF 图。由差分后时间序列的ACF 图和PACF图可以看出，PACF 均呈拖尾衰减，ACF 截尾。初步判断自回归阶数p=3，滑动平均阶数q=0。P、Q的定阶比较困难，根据文献［11］，模型中的参数P、Q阶数一般在2 以内，故我们选择0、1、2 进行由低阶到高阶逐个建模，根据SBIC 和AIC 最小的原则，选择最佳模型（图4、5）。

模型参数估计及检验在尝试不同模型参数后，经白噪声检验和模型参数检验获得3 个备选模型（表1、2）。

图4 差分后T2DM 患者PTB 发病率序列自相关图Fig 4 Autocorrelation function graph of differenced PTB incidence series in T2DM patients

图5 差分后T2DM 患者PTB 发病率序列偏自相关图Fig 5 Partial autocorrelation function graph of differenced PTB incidence series in T2DM patients

表1 备选模型拟合效果及Box-Ljung Q 检验结果Tab 1 Fitted effect of alternative models and results of Box-Ljung Q test

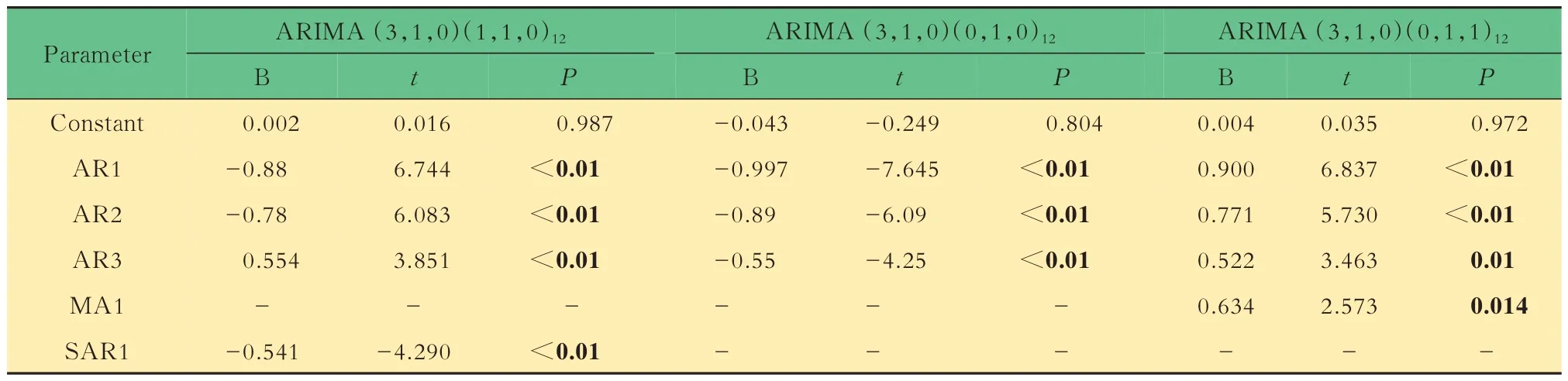
表2 备选模型参数估计Tab 2 Parameter estimations for alternative models

根据以上结果，综合考虑SBIC 和AIC，最终确定最佳模型为ARIMA（3，1，0）（1，1，0）12（不包含常数）。残差序列的Box-Ljung Q 检验P＞0.05，可以认为残差序列是白噪声序列，且模型的参数都有统计学意义。模型残差序列的自相关系数和偏自相关系数均在95%CI 内，进一步验证了残差已是随机分布的白噪声序列，说明所选的模型是恰当的（图6）。模型表达式为：

图6 上海市2010—2014 年T2DM 患者PTB 发病率残差序列自相关图（左）和偏自相关图（右）Fig 6 Autocorrelation（left）and partial autocorrelation（right）graphs of residual sequence of PTB incidence in T2DM patients in Shanghai from 2010 to 2014

ARIMA（3，1，0）（1，1，0）12模型拟合2010—2014年T2DM 患者PTB 发病率：RMSE=4.05，MAPE=5.8%。

ARIMA-SVM 组合模型将2010—2014 年上海市T2DM 患者PTB 发病率ARIMA 模型拟合值与实际值的残差序列使用SVM 模型进行拟合，残差SVM 预测模型参数：核函数为radial 函数，惩罚常数cost=10，γ=0.1。将SVM 残差预测值加上ARIMA 预测值，得到组合模型PTB 发病率预测值。ARIMA 模型和ARIMA-SVM 组合模型得到的2015 年PTB 发病率月预测值见表3。

表3 2015 年上海市T2DM 患者PTB 月发病率的两种模型预测值比较Tab 3 Comparison of predicted values of the two models based on monthly incidence of PTB in T2DM patients in Shanghai，2015

模型预测效果评估由表3 可知，ARIMA 模型预测上海市2015 年T2DM 患者PTB 发病率的MAPE 为87%，RMSE 为2.96；ARIMA-SVM 组合模型的MAPE 和RMSE 均小于单纯ARIMA 模型，提示ARIMA-SVM 组合模型有效校正了ARIMA模型预测值的残差。但两个模型的MAPE 值都较大，预测精度都有待提高。

讨论

随着预测理论及预测技术的不断发展和完善，许多统计理论、预测方法和预测模型都被应用到传染病的预测中。常见的传染病预测模型有ARIMA模型、灰色模型、Markov 模型、人工神经网络模型、通径分析模型等［12］。SVM 也被越来越多地应用到农业［13］、通讯［14］、传染病等领域［15］，与传统模型相结合进行预测，均发现组合模型的预测效果高于单一模型。

本研究基于2010—2014 年上海市户籍T2DM患者中PTB 发病人数，建立并比较了不同参数的ARIMA 模型预测2015 年T2DM 患者PTB 发病的效果，得到最优模型进行拟合。利用拟合值与实际值之间的残差序列作为样本集，运用SVM 预测残差，建立ARIMA-SVM 混合模型。通过比较两个模型的MAPE 和RMSE，发现SVM 有效拟合了原始序列的非线性部分，ARIMA-SVM 混合模型的预测效果优于单一ARIMA 模型。

ARMIA 拟合2010—2014 年PTB 发病率的效果也较好，比较ARIMA 模型和ARIMA-SVM 混合模型的MAPE 值可以发现，两个模型的预测精度还存在较大的提升空间。这可能与PTB 发病率较低且变化不稳定有关。其次，可能是因为ARIMA 分析要求序列是平稳序列，虽然可以通过差分将非平稳序列转化为平稳序列，但是差分意味着信息的损失，导致ARIMA 在预测时误差较大。此外，时间序列分析的基本思想是将预测对象随时间变化而形成的序列看作一个随机序列，其要求序列的变化只与时间有关。在现实社会中，PTB 发病率受经济、文化、医疗水平等多种因素的影响。本研究通过ARIMA 模型预测得到的PTB 发病人数明显高于实际值，这可能与近年来PTB 防治工作有关。本研究结果可为PTB 防治措施的有效性提供了间接证据。

上海市糖尿病管理系统和结核病监测系统建立比较完善，数据体量大，资料比较完整，可以进一步延长观察时间，利用更长年份T2DM 患者结核发病月数据进行建模和预测，比较不同单一模型和组合模型的拟合效果。需强调的是，本次预测只是从数据上反映了传染病的发病规律，有助于预测传染病的发病趋势及负担，但并不能用于探讨传染病发病的影响因素。当前，国家要求开展重点人群结核病的筛查，糖尿病患者的结核病发病情况备受关注，一些特异的防控策略和措施可能已经影响了该人群结核病的发病情况。采用ARIMA-SVM 进行预测，与观察到的实际情况进行比较，可在一定程度上反映这些防控策略和措施的效果。

本研究初次比较了单一ARIMA 预测模型与组合模型在T2DM 患者PTB 发病预测中的应用，研究结果支持组合模型在该人群中应用的有效性。尽管预测效果仍然不理想，但在一定程度上提示当前PTB 防治措施的效果。将来需要继续更新数据，优化混合模型的参数，准确估计T2DM 患者的PTB发病情况及疾病负担，指导公共卫生工作者做好重点人群的疾病防控工作。