Error-based observer control of an optic-electro tracking control system

Xu Tianrong, Ruan Yong, Zhao Zhiqiang,Wang Zongyou, Tang Tao*

Error-based observer control of an optic-electro tracking control system

Xu Tianrong1,2,3, Ruan Yong1,2, Zhao Zhiqiang1,2,Wang Zongyou1,2, Tang Tao1,2,3*

1Key Laboratory of Beam Control, Chinese Academy of Sciences, Chengdu, Sichuan 610209, China;2Institute of Optics and Electronics, Chinese Academy of Sciences, Chengdu, Sichuan 610209, China;3University of Chinese Academy of Sciences, Beijing 100049, China

For an optic-electro tracking system, an image sensor such as charge-coupled device (CCD) cannot provide target trajectories except for line-of-sight (LOS) error. Thus, it is difficult to achieve direct feedforward control for the tracking loop, which determines the closed-loop performance. An error-based observer (EBO) control of a CCD-based tracking loop is proposed to enhance the tracking performance for an optic-electro tracking system on moving platforms. The EBO control can be plugged into an existing feedback control loop. The closed-loop performance of the CCD-based control system can be improved by optimizing the feedforward filter(). Because this EBO method relies only on the final LOS error, it benefits the control system both in disturbance suppression and target tracking and it can be applied to an optic-electro tracking system in moving platforms as well as in ground platforms. An optimal31filter rather than a low-pass filter is improved for this EBO control. Simulations and experiments show that the tracking performance is effectively enhanced in low frequency compared to traditional control methods.

line of sight error; moving platforms; feedforward control; optic-electro tracking systems

1 Introduction

Image sensors (such as charge-coupled device, CCD) are usually used to detect the line of sight (LOS) error in an optic-electro tracking control system, which is used for monitoring and positioning as well as tracking an interesting target. High control bandwidth facilitates good closed-loop performance. However, sampling frequency and time delay of CCD (mainly include exposure time, image process time and transmit time) are the main factors that restrict tracking bandwidth, resulting in reducing tracking accuracy. How to improve closed-loop performance and compensate time delay of CCD with a limited sampling frequency is important research. Using a high-gain feedback controller or improving the order of the control system is a common method, but it has an impact on the dynamic performance of the system, even lead to instability[1-4]. Experiments verified that feedforward control is an effective way to improve tracking performance. Theoretically, it has little influence on closed-loop stability due to its independence from the feedback loop. However, an image sensor such as CCD cannot provide target trajectories except LOS error, which leads to difficulty in achieving feedforward control for image tracking loop[5-6]. A direct feedback loop is still utilized to control LOS in many cases. In addition, motivated by application requirements, more and more optoelectronic tracking systems are equipped on moving vehicles such as ships, aircraft, and spacecraft for diverse missions which makes optical tracking devices more flexible. But this change also brings problems for control systems. The carrier motion at different frequencies such as the sway of the ship or vibration of the satellite will produce direct influence on the line of sight which may affect the tracking performance or even lead to instability. Many methods have been developed to isolate the line of sight from carrier motion[7-12]. In most cases, extra inertial sensors are needed to detect the carrier motion relative to inertial space. It brings difficulties to the implementation of some methods that can be utilized on ground tracking. For example, a method based on data fusion, which combines the line of sight error and angular position to generate feedforward control[13]. It cannot be directly applied to a moving platform, because the platform motion cannot be measured by the non-inertial encoder it used. Extra sensor is necessary. When an inertial measurement unit (IMU) is added, the effectiveness is affected by the attitude accuracy. Generally, the effectiveness of generating feedforward control through data fusion depends on the effectiveness of the synthesized feedforward signal which is determined by the precision of the sensors and the prediction accuracy[14-16]. Inaccurate feedforward signal willreduce the tracking accuracy and even lead to system instability. Based on this situation, an error-based observer (EBO) control of a CCD-based tracking loop is proposed to enhance the tracking performance on the moving platform. The EBO control method does not need extra sensors. It combines the LOS error and output of the position controller to achieve high gain, forwarding into the original closed-loop control system to achieve equivalent feed forward control. Simulations and experiments verified that the EBO control benefits the control system both in disturbance suppression and target tracking. It is based on Youla–Kuˇcera parameterization and its performance can be optimized by the feedforward filter Q. Section 2 gives a detailed analysis of a classical feedforward control and the error-based observer control (EBO) on the moving platform, and makes some remarks on the advantage of the EBO method as compared to the classical feedback control. Section 3 analyzes the system stability and focuses on the parameter design, mainly including the proportional-integral (PI) controller and the low-pass filter(). Section 4 presents the simulation results and the experiment results. Concluding remarks are presented in Section 5.

2 Analysis of control methodologies

2.1 Classical controller for the moving platform

On the moving platform, pointing control is usually implemented via two servo loops, the outer tracking or pointing loop to control LOS error and an inner stabilization or rate loop to isolates the LOS from platform motion. The stabilization loop bandwidth must be high enough to reject the platform disturbance spectrum[17-18]. A classical feedback control structure of Fig. 1 is shown in Fig. 2 where inertial sensors such as gyros feedback the carrier motion to isolate the LOS from platform motion and an image sensor such as CCD detects the LOS error to achieve object tracking.0is the time-delay of CCD,p() is the position controller,v() is the velocity controller,v() is the control plant,() is the target trajectory, and() represents the outer disturbance. The characteristic of the controlled plant for the outer loop is

Fig. 1 The basic structure of the control system based on CCD vision tracking

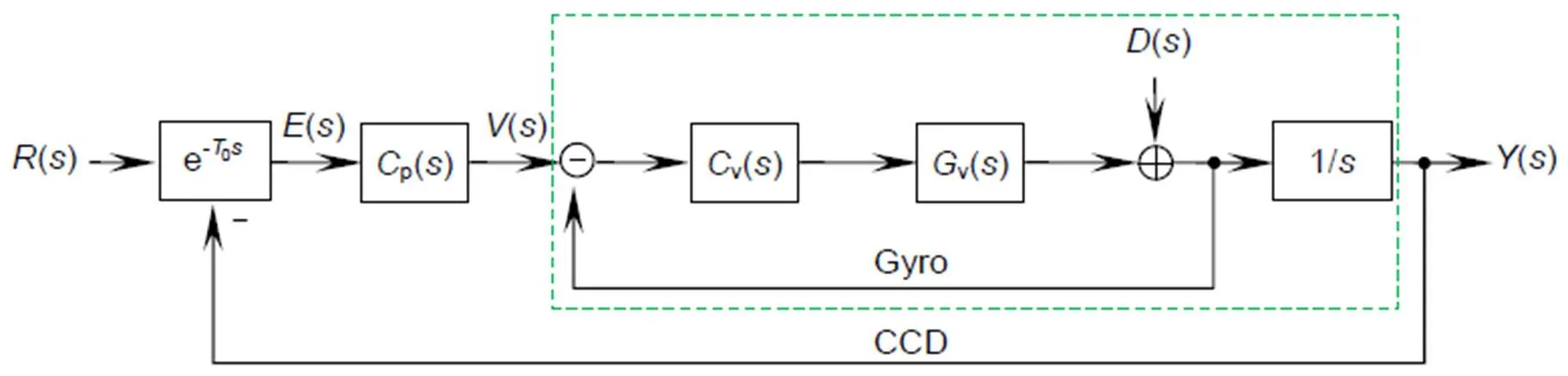
Fig. 2 Configuration of classical feedback control on the moving platform

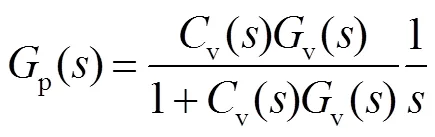
When the velocity closed loop has a much higher bandwidth than that of the position closed loop,v()v()/[1+v()v()]≈1 andp()≈1/are reasonable to some extent. In this case, the outer position loop plays a decisive part in tracking performance. The transform functionorgand sensitivity functionorgof the control scheme is given by Eqs. (2) and (3).

It is not hard to find thatorg+org=1, which means that there is a conflict between tracking performance and disturbance rejection. Obviously, increasing the gain ofp() which means a higher bandwidth is an effective way to improve the tacking performance. But, the tracking bandwidth of the actual optical-electro devices cannot be increased unlimited due to the mechanical resonance and system noise. Besides, high gain may affect the robustness of the control system. From another point, it is meaningless to increasing the bandwidth without limit when the time delay of CCD cannot be cut to zero[19].

A classical feedforward control scheme for object tracking and disturbance rejection is shown in Fig. 3 where0is the time delay of CCD,() is the position controller,() is the control plant,() is the target trajectory,() is the outer disturbance, and() andf() are the feedforward controllers for object tracking and disturbance suppression, respectively. The transfer function of the control scheme is given by:

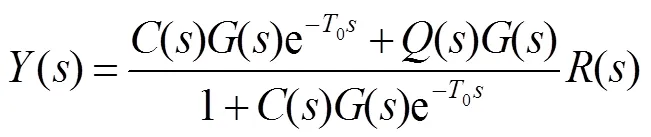
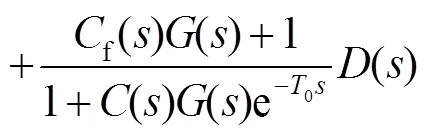
Obviously, whenf()=-1/(),() is independent of(), and when()=1/(),()=() which means perfect real-time tracking. However, it cannot be realized in most cases. First of all, trackers like CCD could not detect the trajectory() except for LOS error(). Second, the accurate detection of() is not easy to realize. Besides, inaccuracy detection of() especially in high frequency also having an influence. Recovering the trajectory() by data fusion and velocity prediction are effective ways to achieve equivalent feedforward control. But some methods cannot be applied to the moving platform directly due to carrier motion and characteristic of sensors and its effectiveness relies on the effectiveness of the synthesized feedforward signals which is determined by the precision of the sensors and the prediction accuracy. Inaccurate feedforward signal will reduce the tracking accuracy and even lead to system instability. So, there is a need of a new control method that can be applied to the moving platform and do not rely excessively on extra sensors.

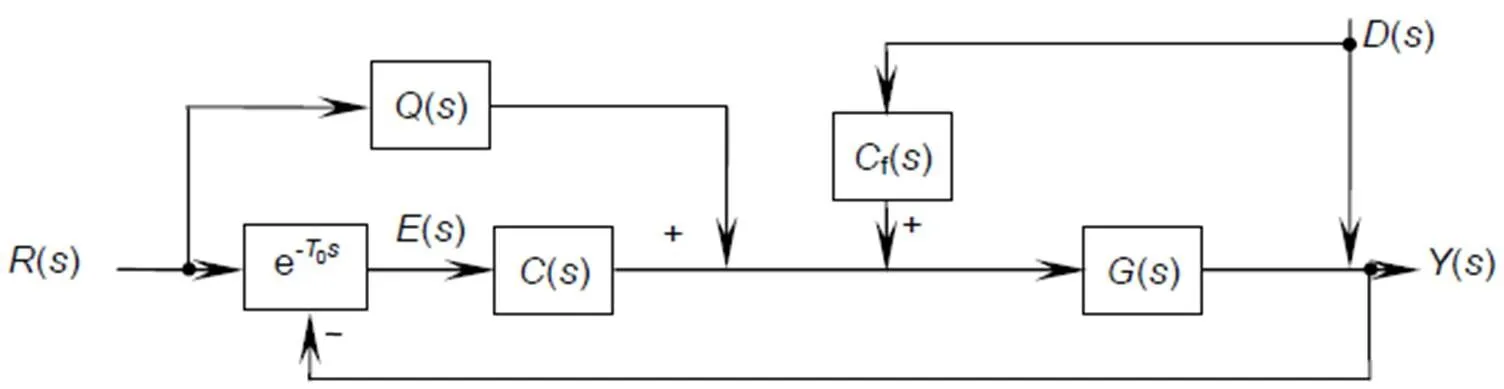
Fig. 3 A classical feedforward control scheme

2.2 The error-based observer (EBO) control method

An error-based observer (EBO) control method which is based on Youla–Kuˇcera parameterization is shown in Fig. 4. It feedforwards the combination of the LOS error from the CCD and the controller output into the originally closed-loop control system.0is the time-delay of CCD,() is the control plant,() is the position controller,-1() is the inverse of(),() is a low-pass filter,() represents the target trajectory,() is the LOS error from the CCD, and() is the outer disturbance which is small when the system in inertial stable status through stabilization control of the inner loop. The sensitive functions for trajectory() and disturbance() of Fig. 4 are given as follow:

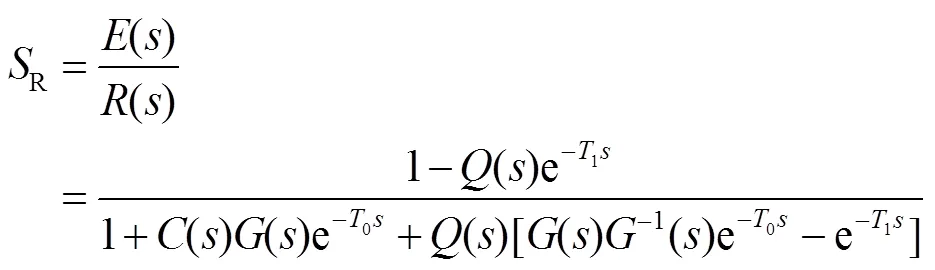
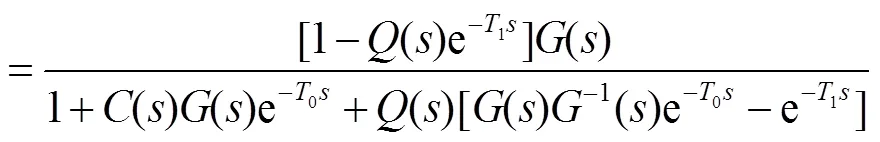
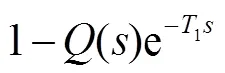
3 Optimal design of parameter

where

Fig. 4 The error-based observer (EBO) control scheme

The sensitive function decides that() has to be a low-pass filter. A general form of low-pass filters is generally given by[3]:

here,、are positive integer. It is easy to know excessive order and bandwidth of() can lead to destruction of the stability condition by plant uncertainty and phase loss in the high-frequency region. To meet the requirement of robustness condition which is affected by phase margin and magnitude margin of the open-loop transfer function, a Q31-filter with an appropriate parameteris a compromise solution. When=3,

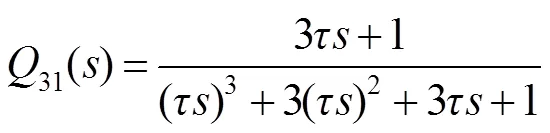
An equivalent controllereq() of Fig. 4 is

After mathematical calculations of Eq. (7), we find it is not easy to satisfym>π/4 andm>6 dB strictly. Several groups of parameters that can satisfy the requirement of robustness condition is shown in Table 1. In order to get better performance,=0.05 is finally chosen.

4 Simulations and experiments

4.1 Simulation results

According to the previous parameter design, the bode response of the transfer function and the sensitive function of classical feedback control and the EBO method is shown in Figs. 6(a) and 6(b) respectively. It is easy to find that although the tracking bandwidth is not improved with the EBO method, it enhances the tracking performance in the low frequency compared to the classical feedback control (CFC) mode. The EBO control mode with1()=1/(0.1+1) improves below 1 Hz compared to classical feedback control. The EBO control mode with an optimal31() with=0.05 is more efficient in frequencies lower than 1 Hz. The experimental verification is depicted in the next section.

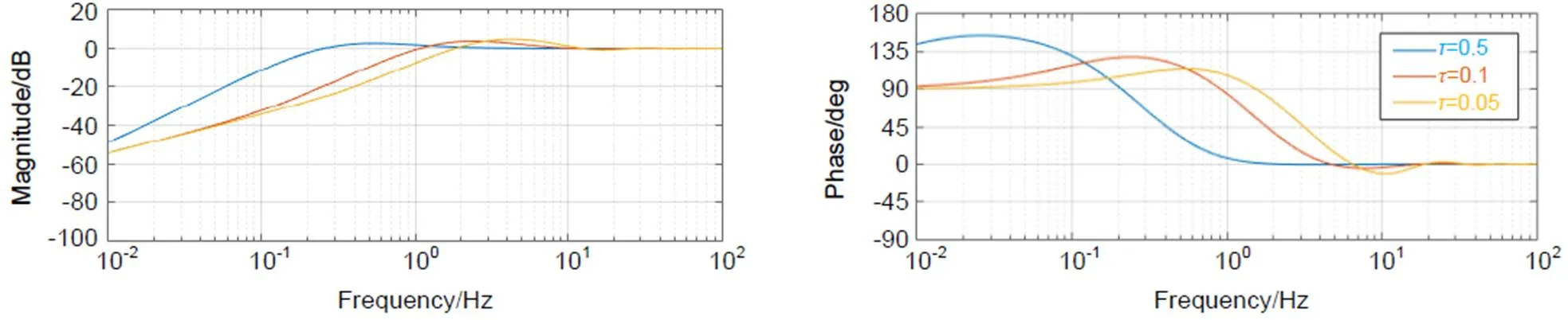
Fig. 5 Bode diagram of 1-Q(jω)e-0.03jω

Table 1 Comparison of gain margin and phase margin among different methods

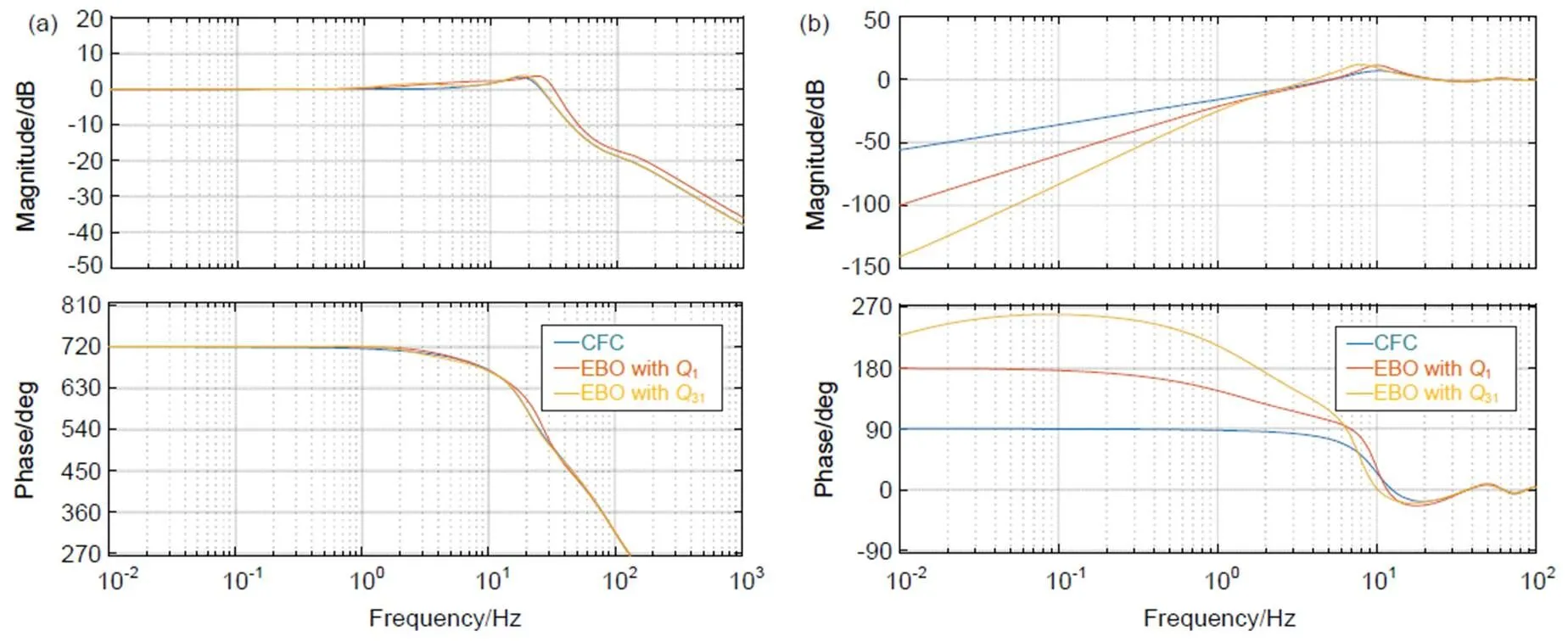
Fig. 6 Bode response of the closed-loop transfer function (a) and sensitivity function (b) from simulations

4.2 Experiment results

The experimental system is shown in Fig. 7. A CCD is used to detect the LOS error with a sampling frequency of 100 Hz. Laser light and FSM2 simulate the target trajectory, FSM1 is the tracking controller and FSM3 is used to simulate the carrier motion. Here, we set the carrier motion=0, which means that FSM3 is fixed. It is reasonable, because FSM3 and FSM2 have the same effect on LOS and it does not matter whether FSM2 or FSM3 generate carrier motion.Besides, according to the control mode analysis in chapter 2, when the system is in the inertial stable status through stabilization control of the inner loop, the remaining disturbance can be neglected compared with the target moving. The target trajectory() is a sinusoidal signal with an amplitude of 0.5 V, which can be expressed as=sin(). The experiment only presents a single axis of the azimuth due to the similarity. We record the LOS error respectively using three different control strategies when=0.05 Hz, 0.1 Hz, 0.5 Hz, and 1 Hz which are depicted in Figs. 8(a)~8(d), respectively. It is obvious that the EBO method has obvious improvement in frequencies lower than 1 Hz compared to classical feedback control, showing an improvement of 8 dB at 1 Hz and 15 dB at 0.05 Hz. The optimal filter()=31() is more efficient than a first-order low-pass filter1() which is consistent with simulation results. But the result of the EBO method with1and31is hard to distinguish and the improvement is not as good as simulation results in frequencies lower than 0.1 Hz, which is a result of the mechanical resonance and system noise.

Fig. 7 Configuration of experimental platform

5 Conclusions

In this paper, an error-based observer (EBO) control method of a CCD-based tracking loop is proposed to enhance the closed-loop performance. This EBO method combines the line-of-sight error and control output to generate a high gain observer. It can be plugged into the existing feedback control loop and the closed-loop performance can be improved by optimizing the feedforward filter(). Simulations and experiments verify that this EBO control method can effectively enhance the closed-loop performance in the low frequency in comparison with the classical control mode and an optimal31filter is more effective than a first-order low pass filter in this EBO control mode. In fact, better performance in the low frequency is more important than a higher bandwidth in many cases especially when the target is far from the tracking device. It is valuable for engineering applications. It is meaningful to explore other Q filters that can be applied to different scenarios. A further experiment on other moving platforms such as gimbals is also needed to verify the method.

[1] Beals G A, Crum R C, Dougherty H J,. Hubble space telescope precision pointing control system[J]., 1988, 11(2): 119–123.

[2] Wang C C, Hu L F, Wang Y K,. Time delay compensation method for tip-tilt control in adaptive optics system[J]., 2015, 54(11): 3383–3388.

[3] Esmaeili M, Shirvani M. Time delay compensation by A PID controller[C]//, Shah Alam, Malaysia, 2011.

[4] Natori K, Tsuji T, Ohnishi K,. Time-delay compensation by communication disturbance observer for bilateral teleoperation under time-varying delay[J]., 2010, 57(3): 1050–1062.

[5] Huang Y M, Ma J G, Fu C Y. Velocity-forecast filters of theodolite[J]., 2003, 5082: 87–93.

[6] Wei Z H. Feedforward control strategies for tracking performance in machine axes[J]., 2005, 18(1): 5–9.

[7] Hurák Z, Řezáč M. Combined line-of-sight inertial stabilization and visual tracking: Application to an airborne camera platform[C]//, Shanghai, 2009.

[8] Deng C, Tang T, Mao Y,. Enhanced disturbance observer based on acceleration measurement for fast steering mirror systems[J]., 2017, 9(3): 6802211.

[9] Wu C, Lin Z. Disturbance observer based control system design for inertially stabilized platform[J]., 2012, 8542: 85420T.

[10] Tian J, Yang W S, Peng Z M,. Inertial sensor-based multiloop control of fast steering mirror for line of sight stabilization[J]., 2016, 55(11): 111602.

[11] Luo Y, Huang Y M, Deng C,. Combining a disturbance observer with triple-loop control based on MEMS accelerometers for line-of-sight stabilization[J]., 2017, 17(11): 2648.

[12] Luo Y, Mao Y, Ren W,. Multiple fusion based on the CCD and MEMS accelerometer for the low-cost multi-loop optoelectronic system control[J]., 2018, 18(7): 2153.

[13] Tang T, Cai H X, Huang Y M,. Combined line-of-sight error and angular position to generate feedforward control for a charge-coupled device–based tracking loop[J]., 2015, 54(10): 105107.

[14] Tang T, Niu S X, Ma J G,. A review on control methodologies of disturbance rejections in optical telescope[J]., 2019, 2(10): 190011.

[15] Yan L J, Huang Y M, Zhang Y H,. Research on the application of RANSAC algorithm in electro-optical tracking of space targets[J]., 2019, 46(11): 180540.

严灵杰, 黄永梅, 张涯辉, 等. RANSAC算法在空间目标光电跟踪中的应用研究[J]. 光电工程, 2019, 46(11): 180540.

[16] Tang T, Tian J, Zhong D J,. Combining charge couple devices and rate sensors for the feedforward control system of a charge coupled device tracking loop[J]., 2016, 16(7): 968.

[17] Kennedy P J, Kennedy R L. Direct versus indirect line of sight (LOS) stabilization[J]., 2003, 11(1): 3–15.

[18] Masten M K. Inertially stabilized platforms for optical imaging systems[J]., 2008, 28(1): 47–64.

[19] Zhang W L, Tomizuka M, Wei Y H,. Robust time delay compensation in a wireless motion control system with double disturbance observers[C]//, Chicago, 2015: 5294–5299.

Error-based observer control of an optic-electro tracking control system

Xu Tianrong1,2,3, Ruan Yong1,2, Zhao Zhiqiang1,2, Wang Zongyou1,2, Tang Tao1,2,3*

1Key Laboratory of Beam Control, Chinese Academy of Sciences, Chengdu, Sichuan 610209, China;2Institute of Optics and Electronics, Chinese Academy of Sciences, Chengdu, Sichuan 610209, China;3University of Chinese Academy of Sciences, Beijing 100049, China

The error-based observer control (EBO) structure

Overview:For an optic-electro tracking system, image sensors (such as CCD) are usually used for monitoring and positioning as well as tracking a target, but they can only detect line-of-sight (LOS) error and cannot provide target trajectories. Therefore, it brings difficulties to the application of feedforward control which is an effective way to improve tracking performance. As a result, recovering the target trajectory through data fusion is an effective way. However, it needs extra sensors and the effectiveness of the equivalent feedforward control method is based on the accuracy of the synthesized feedforward signal which is affected by the measurement accuracy of the sensor and the prediction accuracy. Inaccurate feedforward signal has no improvement in tracking performance and even leads to instability of the control system. When it comes to tracking system on a moving platform, an inertial measurement unit (IMU) is necessary. The attitude accuracy determined by the IMU always plays an import part in tracking performance. Therefore, the equivalent feedforward control method based on data fusion is not applicable in many cases. For traditional feedback control, high control bandwidth facilitates good closed-loop performance. However, the sampling frequency and time delay of the image sensor are the main factors that restrict tracking bandwidth. Simply using a high-gain feedback controller or improving the order of the control system will decrease the dynamic performance of the system, leading to instability. The error-based observer (EBO) control of an image-based tracking loop is proposed to enhance tracking performance for an optic-electro tracking system on the moving platform. This EBO method combines the LOS error and control output to achieve high gain. The equivalent feedforward control can be plugged into the existing feedback control loop. The closed-loop performance of the image-based control system can be improved by optimizing the feedforward filter(). Since this EBO method does not need extra sensors and it benefits the control system in both disturbance suppression and target tracking, it can be applied to both moving platforms and ground platforms. The control structure decided that() has to be a low-pass filter. In this paper, an optimal three-order31filter rather than a low-pass filter is improved for this EBO control. Simulations and experiments show that the tracking performance of the EBO method is effectively enhanced in the low frequency compared to traditional control methods and an optimal31filter is more efficient than a simple first-order low-pass filter. This improvement is meaningful because better performance in the low frequency is more important than in the high frequency for many cases.

Citation: Xu T R, Ruan Y, Zhao Z Q,. Error-based observer control of an optic-electro tracking control system[J]., 2020,47(11): 190713

基于误差的观测器在光电跟踪系统中的应用

徐田荣1,2,3，阮 勇1,2，赵志强1,2，王宗友1,2，唐 涛1,2,3*

1中国科学院光束控制重点实验室，四川 成都 610209；2中国科学院光电技术研究所，四川 成都 610209；3中国科学院大学，北京 100049

对于光电跟踪系统来说，图像传感器例如电荷耦合器件(CCD)只能够探测脱靶量即偏差信息，而无法得到目标运动轨迹，所以，大多数情况下在目标跟踪回路不能直接实现前馈控制，这限制了系统的闭环跟踪性能。本文采用了一种基于误差观测器的等效前馈控制方法来提高运动平台光电跟踪系统的跟踪性能。该方法是在原有的反馈控制回路的基础上加入一个观测前馈通路，通过优化前馈滤波器提高闭环性能。由于是基于最终的视觉误差的观测，该方法对目标跟踪和扰动抑制同时起作用，既可以应用到地基跟踪也可以应用于运动平台上。前馈滤波器没有采用简单的一阶低通滤波器而是选择31滤波器。仿真和实验表明，与传统控制方法相比，这种基于误差观测器的控制方法能够有效提高系统的低频跟踪性能。

视轴偏差；运动平台；前馈控制；光电跟踪系统

TP273

A

徐田荣，阮勇，赵志强，等. 基于误差的观测器在光电跟踪系统中的应用[J]. 光电工程，2020，47(11): 190713

2019-11-27；

2020-01-14

中国科学院青促会基金资助项目

徐田荣(1994-)，女，硕士研究生，主要从事运动平台光电跟踪系统前馈控制技术。E-mail：1160255376@qq.com

唐涛(1980-)，男，博士，研究员，主要从事光电工程领域中控制理论以及工程应用的研究。E-mail：taotang@ioe.ac.cn

: Xu T R, Ruan Y, Zhao Z Q,Error-based observer control of an optic-electro tracking control system[J]., 2020, 47(11): 190713

10.12086/oee.2020.190713

Supported by Youth Innovation Promotion Association of Chinese Academy of Sciences

* E-mail: prettang@gmail.com