一种应用于光纤陀螺寻北的温度漂移补偿方法

骆金辉，周一览，刘 承，舒晓武

一种应用于光纤陀螺寻北的温度漂移补偿方法

骆金辉*，周一览，刘 承，舒晓武

浙江大学光电科学与工程学院，浙江 杭州 310027

光纤陀螺寻北启动误差是启动过程温度剧烈变化导致的光纤陀螺零偏漂移产生的误差，表现为冷启动时寻北误差较稳定段时明显增大，事实上延长了有效寻北时间。通过对光纤陀螺温度漂移影响因素的分析，利用经验模态分解、ARMA建模与Kalman滤波建立多参量线性模型，实现了一种应用于光纤陀螺寻北的温度漂移补偿方法，实验结果表明，该方法可以将寻北启动误差降低近80%，使得冷启动时寻北精度与稳定段相当并缩短了有效寻北时间。

光纤陀螺；寻北；温度漂移；温度补偿

1 引 言

寻北定向技术在多个领域有着广泛的应用，在军事领域，各种弹体的发射，海陆空天各种载具的航行都不能没有方位基准；在民用领域，矿藏勘探开采、大地测绘和土木工程建设等也少不了方位基准。

光纤陀螺(Fiber optical gyroscope, FOG)是一种全固态的陀螺仪，原理基于Sagnac效应，具有高灵敏度、耐冲击、集成可靠、低功耗等特点，满足寻北定向系统的应用需求。然而由于光纤陀螺当中有一些主要元器件对温度的变化比较敏感，温度变化就造成了光纤陀螺输出信号出现非互易性相位延迟，致使光纤陀螺的零位漂移发生波动，降低了温度非恒定条件下光纤陀螺的测量精度。因此，在光纤陀螺上电后的启动过程中，温度的变化导致了光纤陀螺冷启动后一段时间内输出信号温度漂移具有较大波动，经过一段时间后才能逐渐稳定。这种启动过程中的特性产生了光纤陀螺的启动漂移，使得在寻北应用中冷启动时会产生寻北启动误差，进而降低了寻北精度。

目前，想要抑制光纤陀螺的温度漂移，主要有对光纤陀螺的内部结构与元器件进行优化、对光纤环的绕制技术进行升级、对光纤陀螺的温度进行控制等方法，但是要从机理上抑制温度漂移，尤其是对于体积较小的中低精度光纤陀螺来说难度很大，而温度漂移建模补偿则是一个简捷有效的解决方法，且能够基本满足工作需求[1]。

常用的光纤陀螺温度漂移补偿模型大概有：线性模型[2]、小波网络模型[3]、神经网络模型[4]、受控马氏链模型[5]、支持向量机[6]、自适应模糊推理[7]等。本文主要针对冷启动状态下寻北过程的温度漂移补偿，面向工程实际设计了基于温度、温度变化率及两者乘积的交叉项的多参量线性补偿模型，并进行实验验证。结果表明，运用了本文的温度漂移补偿方法后，能够抑制启动误差，提高寻北精度，缩短有效寻北时间。

2 光纤陀螺温度漂移原理与补偿模型

2.1 光纤陀螺温度漂移原理

光纤陀螺上电后，由于各元器件的发热及工作环境温度变化等使得光纤陀螺的工作温度发生变化，从而导致光纤陀螺的温度漂移也随之改变，而其中光纤环受温度影响导致的热致非互易性相位延迟是主要影响因素[8]。

当光纤环中存在不对称的温度扰动时，两束传播方向相反的光通过光纤后会产生非互易性相位延迟，即Shupe效应[9]。该非互易性相位延迟和由旋转产生的Sagnac相位延迟混合在一起，影响了光纤陀螺的测量精度。在光纤长度为的光纤环中，两束分别沿顺、逆时针方向传播的相干光，因不对称的温度扰动所产生的非互易性相位延迟为

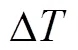
2.2 光纤陀螺温度漂移补偿模型

由于本文目的是为了研究寻北过程的快速化，因此采用了计算量最小的多参量线性模型。目前，线性及多项式建模思路主要是基于IEEE标准(IEEE Std 952-1997)中的光纤陀螺温度漂移模型[11]

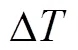
式中：为温度与温度变化率的交叉项敏感系数；为温度的平方项敏感系数；为温度敏感系数；为温度变化率的平方项敏感系数；为温度变化率敏感系数；为常数项。

3 光纤陀螺温度漂移补偿模型建立方法

由于光纤陀螺的输出信号中含有随机漂移高频分量，使得信号的复杂度大大提高，导致模型拟合精度降低，不利于建立温度漂移模型。为了解决这个问题，本文采用了一些方法来降低光纤陀螺输出信号的随机漂移对建模过程的影响。

因为光纤陀螺输出含有随机漂移，直接用于建模存在较大误差，因此需要对光纤陀螺输出进行滤波处理，其中最常用的是Kalman滤波。又因为Kalman滤波需要得到已知的系统方程，所以本文采用自回归移动平均模型(autoregressive-moving average, ARMA)建模的方式得到系统方程。又因为ARMA建模需要满足建立模型的时间序列是一个零均值的平稳随机过程，所以本文采用了经验模态分解(empirical mode decomposition, EMD)方式对趋势项进行分离，具体流程图如图1。

3.1 EMD

EMD是一种数据驱动的自适应时域分解算法，它依据信号自身的特点，按频率自适应地将信号分解为具有物理意义的多尺度时频特性本征模态函数，对非线性及非平稳信号的处理比较适合[12]。

EMD滤波方法主要有两类，一类是直接重构法，直接重构法采用直接移除主要成分为噪声的本征模态函数(intrinsic mode functions, IMF，用IMF表示)，只将剩余项求和得到的重构信号作为滤波结果。由于在滤波过程中滤除了部分有效信号，使得信号会发生一定的变形，而且滤波效果主要受分解精度的影响。而另一类阈值滤波法则改善了这些缺点，因此本文采用了阈值滤波法。运用EMD提取原来非线性非平稳信号中的趋势项，从而使信号符合零均值、平稳性假设，能够符合ARMA建模条件，继而能够进行Kalman滤波处理。具体算法如下[13]：

将光纤陀螺的输出信号输入EMD，通过筛分的方式分解得到若干个从高频到低频的IMF与残差信号：

其中：阶数小的IMF分量主要为高频成分；阶数大的IMF分量则为低频成分。光纤陀螺输出信号EMD处理的主要思想就在于，含噪声的光纤陀螺输出信号的有效能量主要集中在低频段，频段频率越高，有效能量就越低。因此，存在某一阶IMF()分量，使得其后的IMF分量以有效信号为主要成分，而之前的1个IMF分量中则是以噪声为主要成分[14]。本文采用IMF的平均能量作为IMF()的选取判据。第阶IMF的平均能量可以表达为

式中为IMF信号总时间长度。

根据式(5)评估光纤陀螺的输出信号经过EMD分解后各IMF的平均能量，找到平均能量开始由降转增的第个IMF分量，则可以利用从第个开始的IMF作为光纤陀螺有效信号，亦即信号趋势项：

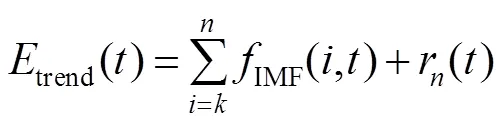
考虑到第个之前的IMF中除了噪声外还存在部分有效信号，将这部分进行ARMA建模与Kalman滤波处理，提取出其中的有效信号，这部分为其余信号

3.2 ARMA

ARMA(，)是时间序列中最为重要的模型之一，它主要由两部分组成：AR表示阶自回归过程，MA表示阶移动平均过程。在一定的近似范围上，任一广义平稳随机过程可由合适阶数的ARMA(，)模型进行近似[15]。设有一零均值平稳随机时间序列{y}，其ARMA模型如下：

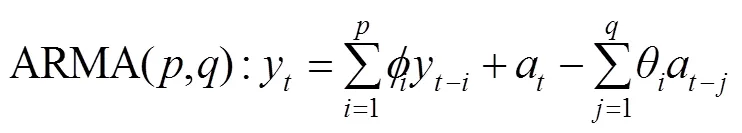
式中：y为时间序列{y}在时刻的数据；为自回归参数；为移动平均参数；a为残差序列，一般为白噪声。

图1 光纤陀螺温度漂移模型建立流程图

3.3 Kalman滤波

在对光纤陀螺输出信号降噪，提高寻北精度中应用最多的滤波方法是Kalman滤波。Kalman滤波方法，又称最优化递归型数据处理算法,是在线性最小均方误差的准则下对信号的最优递归型进行估计，同时其增益矩阵在滤波的过程中随当前的状态量不断进行修正，所以又是一种时变的递推型滤波器。其基本思想是利用上一时刻的估计值与当前时刻的观测值来对状态变量进行估计。

对于平稳线性离散系统，其状态方程的一般形式

其中：表示时刻的状态矢量，–1表示1时刻的状态矢量，表示系统状态的转移矩阵，表示过程噪声矢量系数矩阵，–1表示1时刻系统的过程噪声矢量。

对于平稳线性离散系统，其量测方程的一般形式：

其中：表示时刻系统的观测矩阵，表示系统的观测矢量矩阵，表示时刻系统的状态矢量，表示时刻系统的观测噪声。

进行Kalman滤波最重要条件是需要建立状态方程和量测方程，而状态方程和量测方程的建立，以及Kalman滤波生效需要待滤波的时间序列有一个确定模型方程，因此以上对输出信号的时间序列的模型方程的建立是能够运用Kalman滤波方法的基础。

而将ARMA模型转化为状态空间模型主要有Akaike、Harvey、Aoki三种方法，这里使用了较为常用的Harvey方法。

3.4 模型建立与补偿效果

在静态条件下进行光纤陀螺启动实验，记录光纤陀螺启动过程中的温度及对应光纤陀螺输出，采样频率为1 Hz，光纤陀螺输出信号及温度如图2所示，其中数据单位均为直接测得的数字量。光纤陀螺启动过程是一个温度变化率逐渐减小的升温过程，温度变化率最大值为0.0545 ℃/s。

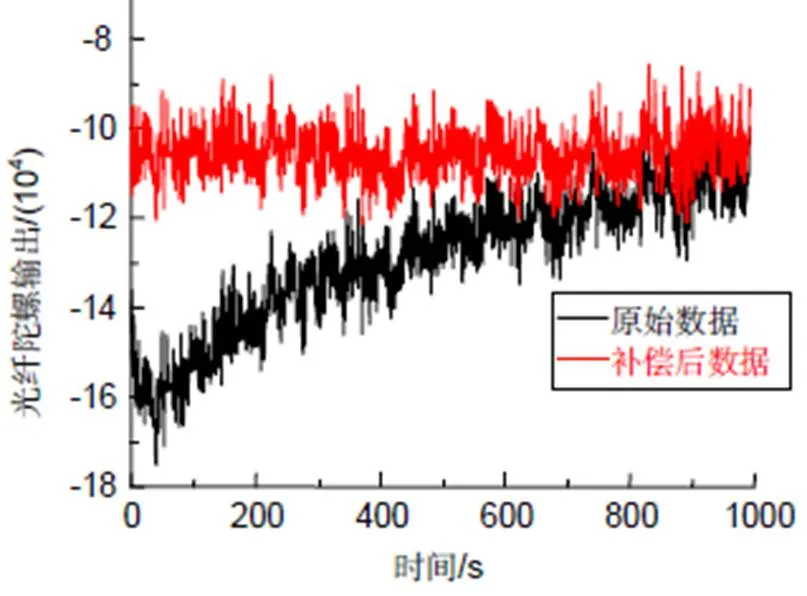
利用建立的温度漂移补偿模型对图2所示的光纤陀螺原始输出数据进行补偿得到结果如图3，光纤陀螺输出信号补偿前后零偏稳定性分别为1.25°/h和0.489°/h，温度漂移补偿效果明显。

图2 光纤陀螺静态实验结果

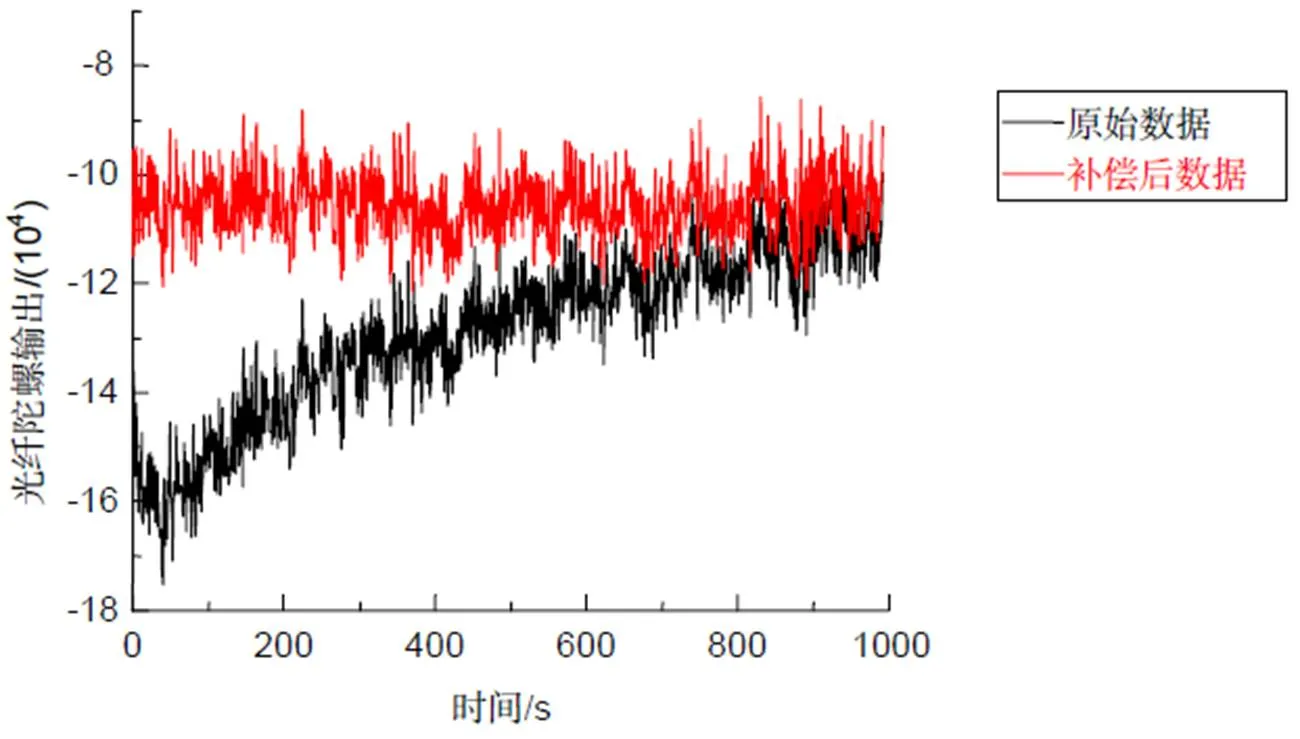
图3 光纤陀螺温度补偿效果

4 寻北实验与结果分析

为验证温度漂移补偿对光纤陀螺寻北启动误差的抑制效果，在室温下对光纤陀螺用四位置法进行了寻北实验[16]。光纤陀螺置于转台上，输入轴垂直于转台转轴保持水平安装。在圆周内等间距取8个方位，在各方位上进行多次光纤陀螺寻北实验，实验中，各位置总采样时间为60 s，采样频率为1 Hz。

寻北实验分为组间断电寻北试验与次间断电寻北试验两项。组间断电寻北试验用于获得启动过程对整体寻北精度的影响以及在上电后经过一段时间的稳定后光纤陀螺的寻北精度，并在此基础上进行温度漂移补偿，以便验证温度漂移补偿算法对于稳定状态下光纤陀螺寻北精度的影响。次间断电寻北试验则用于获得在上电后未经过一段时间的稳定时光纤陀螺的寻北精度，并在此基础上进行温度漂移补偿，从而验证补偿算法对于启动过程中寻北效果改善的有效性。

4.1 组断寻北实验

在与启动实验相同条件下，组断寻北实验共进行8组实验，每组重复寻北实验10次，共80次。各组实验间断电3600 s，以保证光纤陀螺在各方位上的寻北实验的启动过程均相同。为了表现含冷启动过程的整体寻北精度与稳定段寻北精度的差别，故分别计算每组寻北实验中的首次实验数据除去与否的寻北精度，其中去首次实验的数据可以体现启动过程结束后陀螺稳定段的寻北精度。然后将所有数据利用启动实验中得到的温度漂移补偿模型进行补偿后计算寻北精度。得到的寻北精度结果如表1。

可以看出，光纤陀螺在稳定段的寻北精度与含冷启动过程的整体寻北精度有着明显的差异。采用温度漂移补偿后无论是稳定段寻北精度还是整体寻北精度，相对原始数据均有所提升。特别地，采用温度漂移补偿之后光纤陀螺整体寻北精度与稳定段寻北未补偿时精度相当。

4.2 次断寻北实验

次断寻北实验为在与启动实验相同条件下，共进行8组实验，每组重复寻北实验7次，共56次。各组实验间转动转台，改变待测的方位角。各次实验间断电1200 s，以保证光纤陀螺在各方位上的寻北实验的启动过程均相同，使得每次寻北实验均在光纤陀螺冷启动后便直接进行。得到的寻北实验数据先直接进行寻北精度计算，然后利用启动实验中得到的温度补偿模型进行补偿后再次进行寻北精度计算，得到的结果如表2。

可以看出，在光纤陀螺冷启动直接进行寻北时，采用温度漂移补偿之后寻北精度提升了79%，与组断实验时稳定段的寻北精度相当，更表明了本文提出的温度漂移补偿方法能够消除光纤陀螺的寻北启动误差，从而提高光纤陀螺寻北精度，缩短了光纤陀螺有效寻北所需的时间。

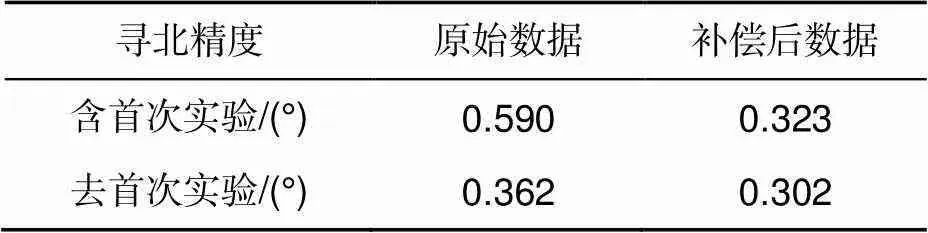
表1 组断实验结果

表2 次断实验结果

5 结 论

光纤陀螺冷启动直接进行寻北时，通过温度漂移建模补偿后，得到的寻北精度比原始数据有显著提升，达到与稳定状态相当的程度。而在光纤陀螺稳定段进行寻北时，通过温度漂移建模补偿后，不影响寻北精度。因此，本文提出的光纤陀螺温度漂移补偿方法能够提高光纤陀螺冷启动直接进行寻北的寻北精度，使得光纤陀螺在冷启动直接进行寻北时也能有较高的精度，从而更好地发挥光纤陀螺快速性的优势，进一步实现寻北过程的快速化，在光纤陀螺其他应用领域，如快速对准，也有很好的工程应用前景。

[1] Han B, Lin Y R, Deng Z L. Overview on modeling and compensation of fog temperature drift[J]., 2009, 17(2): 218–224.

韩冰, 林玉荣, 邓正隆. 光纤陀螺温度漂移误差的建模与补偿综述[J]. 中国惯性技术学报, 2009, 17(2): 218–224.

[2] Dai S W, Zheng B D, Li W G,. Temperature error compensation of fiber optic gyroscope based on multi-parameter model[J]., 2019, 6(4): 78–82.

戴邵武, 郑百东, 李文国, 等. 基于多参量模型的光纤陀螺温度误差补偿[J]. 导航定位与授时, 2019, 6(4): 78–82.

[3] Li J L, Xu H L, He J. Temperature compensation of start-up drift for fiber optic gyroscope based on wavelet network[J]., 2011, 31(5): 0506005.

李家垒, 许化龙, 何婧. 基于小波网络的光纤陀螺启动漂移温度补偿[J]. 光学学报, 2011, 31(5): 0506005.

[4] Li G Y, Hou H L, Du J,. FOG temperature drift compensation method based on wavelet denoising and neural network[J]., 2019, 46(9): 180636.

李光耀, 侯宏录, 杜鹃, 等. 采用小波降噪和神经网络的FOG温度漂移补偿方法[J]. 光电工程, 2019, 46(9): 180636.

[5] Qian F, Tian W F, Yang Y J,. A model on temperature drift of interference fiber optical gyros based on controlled Markov chain[J]., 2003, 14(7): 705–708.

钱峰, 田蔚风, 杨艳娟, 等. 基于受控马氏链的干涉型光纤陀螺温度漂移模型[J]. 光电子·激光, 2003, 14(7): 705–708.

[6] Wang W, Chen X Y. Modeling and compensation method of FOG temperature drift based on multi-scale and improved support vector machine[J]., 2016, 24(6): 793–797.

王威, 陈熙源. 一种基于多尺度和改进支持向量机的光纤陀螺温度漂移建模与补偿方法[J]. 中国惯性技术学报, 2016, 24(6): 793–797.

[7] Liu W T, Liu J Y, Shen Q. Research on multi-scale modeling of temperature drift in fogs[J]., 2019, 41(3): 431–435.

刘文涛, 刘洁瑜, 沈强. 光纤陀螺温度漂移的多尺度建模研究[J]. 压电与声光, 2019, 41(3): 431–435.

[8] Chen Y P, Liang C, Zhang D W,. Magnetic-temperature coupling effect of a fiber optic gyroscope[J]., 2018, 47(5): 0506005.

陈一平, 梁璀, 张登伟, 等. 光纤陀螺磁温耦合效应[J]. 光子学报, 2018, 47(5): 0506005.

[9] Shupe D M. Thermally induced nonreciprocity in the fiber-optic interferometer[J]., 1980, 19(5): 654–655.

[10] Jin J, Song N F, Li L J. Temperature drift modeling and real-time compensation of interferometric fiber optic gyroscope[J]., 2007, 28(6): 1449–1454.

金靖, 宋凝芳, 李立京. 干涉型光纤陀螺温度漂移建模与实时补偿[J]. 航空学报, 2007, 28(6): 1449–1454.

[11] IEEE. IEEE standard specification format guide and test procedure for single-axis interferometric fiber optic gyros: IEEE Std 952-1997[S]. Ne York: IEEE, 1998.

[12] Huang N E, Shen Z, Long S R,. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]., 1998, 454(1971): 903–995.

[13] Liu W T, Liu J Y, Shen Q. Integrated modeling and filtering of fiber optic gyroscope's random errors[J]., 2018, 45(10): 180082.

刘文涛, 刘洁瑜, 沈强. 光纤陀螺随机误差的集成建模及滤波处理[J]. 光电工程, 2018, 45(10): 180082.

[14] Wu Z H, Huang N E. A study of the characteristics of white noise using the empirical mode decomposition method[J]., 2004, 460(2046): 1597–1611.

[15] Zhu K B, Zhang C X, Zhang X Y. Study on modeling and identification of random drift for fog[J]., 2006, 27(5): 1118–1121.

朱奎宝, 张春熹, 张小跃. 光纤陀螺随机漂移ARMA模型研究[J]. 宇航学报, 2006, 27(5): 1118–1121.

[16] Ma Z Y, Zhou Y L. Research on suppression method of north-seeking startup error of fiber-optic gyroscope[J]., 2018, 37(6): 33–35.

马知瑶, 周一览. 光纤陀螺寻北启动误差抑制方法研究[J]. 传感器与微系统, 2018, 37(6): 33–35.

A temperature drift compensation method applied to fiber optic gyroscope north-seeking

Luo Jinhui*, Zhou Yilan, Liu Cheng, Shu Xiaowu

College of Optical Science and Engineering, Zhejiang University, Hangzhou, Zhejiang 310027, China

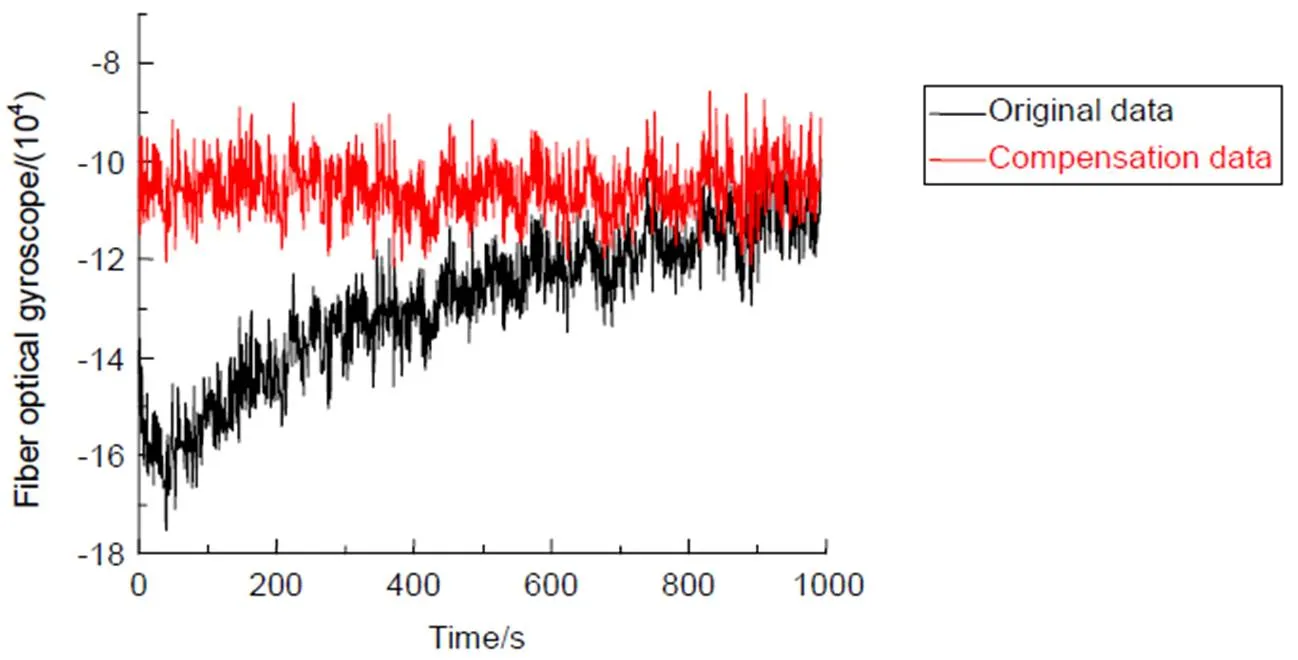
Fiber optic gyro temperature compensation effect

Overview:The north-seeking orientation technology has wide range of applications in many fields. In the military domain, missiles, rockets, artillery, etc. cannot be launched without direction datum. Aerospace, tanks, ships, etc. cannot work without direction datum. In the civilian domain, mineral exploration, mining, geotechnical engineering, and civil engineering construction also require direction datum. Therefore, the research on north-seeking orientation technology is of great significance for realizing national defense modernization and promoting national economic development.

Fiber optical gyroscope (FOG) is an all-solid-state gyroscope based on Sagnac effect. It has the advantages of high impact resistance, high sensitivity, long life, low power consumption, and reliable integration. It is especially suitable for north-seeking orientation system. However, since the main components of FOG are sensitive to temperature, when the temperature changes, non-reciprocal phase errors will occur in the output signal of FOG, resulting in instability of the zero drift of FOG, and ultimately affecting FOG’s accuracy under different temperature conditions. Therefore, the change of temperature during the startup of FOG leads to the phenomenon that the output data of FOG has a large temperature drift after power-on, and then gradually becomes stable. This startup characteristic causes FOG north-seeking startup drift, and north-seeking startup error during the cold start, which is manifested by a significant increase in the north-seeking error during the cold start and actually prolongs the effective north-seeking time.

The method for suppressing the temperature drift of the FOG generally adopts methods of improving the structure and components of the fiber gyro, improving the fiber winding technology, and controlling the temperature of FOG. But suppressing the temperature drift from the mechanism, especially for the medium and low precision FOG with small volume is very difficult. However, the temperature drift modeling compensation is a relatively simple and quick solution, and can basically meet the work requirements. Through the analysis of the factors affecting the temperature drift of FOG, the multi-parameter linear model was established by empirical mode decomposition (EMD), autoregressive-moving average (ARMA) modeling, and Kalman filtering to realize a temperature drift compensation method applied to FOG north-seeking. The experimental results show that the method can reduce the north-seeking startup error by nearly 80%, so that the startup north-seeking precision is equivalent to the stable phase and the effective north-seeking time is shortened.

Citation: Luo J H, Zhou Y L, Liu C,. A temperature drift compensation method applied to fiber optic gyroscope north-seeking[J]., 2020,47(11): 190681

A temperature drift compensation method applied to fiber optic gyroscope north-seeking

Luo Jinhui*, Zhou Yilan, Liu Cheng, Shu Xiaowu

College of Optical Science and Engineering, Zhejiang University, Hangzhou, Zhejiang 310027, China

The startup error of fiber optic gyroscope (FOG) in north-seeking is the error caused by the zero-bias drift of FOG caused by drastic change of the temperature in the starting process. The start-up error significantly increases north-seeking error during the cold startup phase compared to the stable phase, which prolongs the effective north-seeking time. Through the analysis of the factors affecting the temperature drift of FOG, the multi-parameter linear model was established by empirical mode decomposition (EMD), autoregressive-moving average (ARMA) modeling and Kalman filtering to realize a temperature drift compensation method applied to FOG north-seeking. The experimental results show that the method can reduce the north-seeking startup error by nearly 80%, so that the startup north-seeking precision is equivalent to the stable phase and the effective north-seeking time is shortened.

fiber optic gyroscope (FOG); north-seeking; temperature drift; temperature compensation

V241.5

A

骆金辉，周一览，刘承，等. 一种应用于光纤陀螺寻北的温度漂移补偿方法[J]. 光电工程，2020，47(11): 190681

10.12086/oee.2020.190681

: Luo J H, Zhou Y L, Liu C,A temperature drift compensation method applied to fiber optic gyroscope north-seeking[J]., 2020, 47(11): 190681

2019-11-10；

2020-01-21基金项目：国家自然科学基金资助项目(61203190)

骆金辉(1995-)，男，硕士研究生，主要从事光纤陀螺定向技术的研究。E-mail：21730064@zju.edu.cn

Supported by National Natural Science Foundation of China (61203190)

* E-mail: 21730064@zju.edu.cn