5G系统基于PSS和SSS联合频偏估计方法
2020-12-10高尚蕾张治中
高尚蕾,张治中,段 浴,席 兵
(重庆邮电大学 通信与信息工程学院,重庆 400065)
0 引 言
5G 下行采用正交频分复用(Orthogonal Frequency Division Multiplexing, OFDM)技术,频率同步是 OFDM 通信系统中的关键问题[1]。OFDM 系统对载波频偏敏感,频率偏移会降低信号幅度引起相位失真并破坏子载波之间的正交性,从而导致信噪比(Signal Noise Ratio, SNR)的损失[2-5]。为了提高系统的性能,需要采取有效的频偏估计和补偿措施。盲估计算法无需插入导频,可以节省频谱资源,但精度较低[6-7];文献[8]提出了一种改进的时域数据辅助联合载波频偏和时偏估计方法,提高了估计精度,但引入了迭代链路,导致计算复杂度太大难以工程应用;文献[9]提出了一种使用训练序列代替传统第M次幂运算的频偏估计算法,算法精度大幅提升,但对同步要求较高,算法计算量大,难以满足5G的低时延要求;文献[10-11] 提出了一种基于训练序列的频偏估计算法,有效地提高了频偏估计精度,但工程中难以实现;文献[12-13]提出了一种 OFDM 系统基于循环前缀(Cyclic Prefix, CP)的频偏估计算法,但受噪声、多径和信道衰落影响较大,在实际工程中并不适用。
本文在基于主同步信号(Primary Synchronization Signal, PSS)的频偏估计算法基础上,联合辅助同步信号(Secondary Synchronization Signal, SSS)进行频偏估计,在保证算法精度的同时增大了频偏估计范围。在5G系统中,本文所提算法估计精度高、估计范围大且实现简单,适合工程实现。
1 系统模型和频偏影响
5G下行采用OFDM系统模型,通过最小二乘(Least Squares, LS)算法计算出参考信号位置初始信道响应,则频偏为fd的时域接收信号的第l个 OFDM 符号可表示为[14]
式中:n为采样点;N为子载波个数;Xl(i)为第i个子载波在第l个OFDM符号上发送的信息;Hl(i)为第i个子载波在第l个OFDM符号上的信道响应值;j为虚数单位;wn为高斯白噪声。对时域信号进行快速傅里叶变换(Fast Fourier Transform,FFT)得到频域信号,可表示为

式中,第1项表明当前OFDM符号受到幅度衰落相位旋转影响,第2项表明当前子载波受到相邻子载波干扰,使得子载波之间正交性受到破坏。
2 基于PSS的频偏估计算法
文献[15]提出了一种基于PSS的频偏估计算法。 假设5G时域信道变换缓慢时, 由协议3GPP 38.211可知,在一个时隙里,当存在同步信号和物理广播信道块(Physical Broadcast Channel,PBCH)(Synchronization Signal and PBCH Block, SSB)时, PSS在第4和第8(或第2和第8)个OFDM 符号中对应的相同子载波位置。所以直接用不同OFDM 符号中的PSS接收信号进行互相关计算得到相关序列corrm(k),设d为相关信号所在OFDM的符号间隔,其频偏估计值为
式中:NCP为循环前缀长度;NR为接收天线个数;Nk为当前OFDM内PSS个数;Δf为子载波间隔。该算法的频偏估计范围为[-Δf·N/[2d(N+NCP)],Δf·N/[2d(N+NCP)]],其计算复杂度低,易于实现,但因受OFDM符号距离影响导致估计范围较小,估计精度不高。
3 基于PSS和SSS的联合频偏估计算法
3.1 算法总述
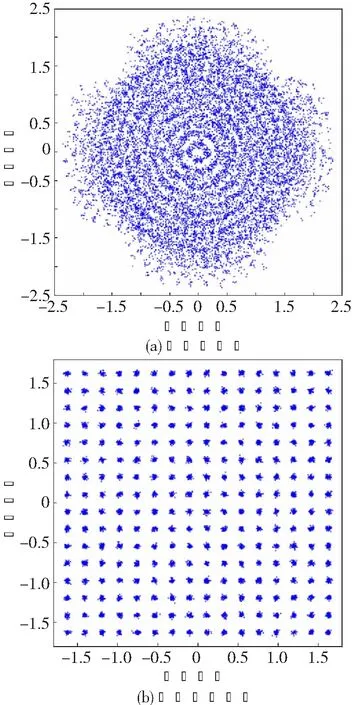
在时域信道变换缓慢的情况下,参照3GPP 38.211协议,以Case B、3 GHz 图1 无线帧结构 由式(3)可知: 基于上述分析,修正后的频偏值fd_final可表示为 式中:fd为实际频偏值;fd_final为估计值;δ为FFT后的SNR。在缓慢变化的信道中,随着符号间隔变长,MSE逐渐减小,所以采用长间隔参考信号估计频偏值修正短间隔参考信号估计频偏值来获得更好的精度。 为验证对比算法的性能,仿真采用相同系统参数。假设系统接收端和发送端完全同步,系统配置如表 1 所示。 表1 仿真参数 图2所示为SNR为20 dB时本文算法的估计范围。由仿真图可知,在算法估计范围内频偏估计结果与真实值基本重合,超出算法估计范围时频偏估计精度急速下降,说明算法在估计范围内可以准确估计出频偏值。 图2 频偏估计范围 图3所示为不同频偏估计算法在不同SNR下的MSE仿真图。由图可知,在AWGN信道下, 随着SNR的增大,3种算法的MSE都随之下降,且本文算法MSE均低于基于CP和基于PSS的频偏估计算法, 表明本文算法比其余两种算法拥有更高的精度,且在低SNR下本文算法依旧拥有很高的精度。 图3 不同频偏估计算法性能比较 图4(a) 所示为在频偏值为500 Hz、SNR为30 dB情况下无频偏修正信号的星座图。由图可知,在没有用本算法进行频偏修正前,接收信号的星座图为发散状态且存在相位旋转,导致接收信号无法正确解调;图 4(b) 所示为在频偏值为500 Hz、SNR为 30 dB情况下频偏修正后信号的星座图。由图可知,在本算法进行频偏修正后,信号星座图为聚拢状态且消除了相位旋转,有利于接收信号的正确解调。 图4 修正信号星座图 图5所示为系统在频偏为500 Hz时频偏修正前后的误比特率(Bit Error Rate, BER)仿真图。由图可知,3种算法的BER均随着SNR的增加而降低,本文基于PSS和SSS的联合频偏估计算法的BER性能比基于CP和基于PSS的频偏估计算法更低。 图5 不同算法频偏修正前后系统BER比较 本文利用PSS和SSS信道估计值做相关来计算频偏并进行修正。仿真结果表明,本文所提算法在AWGN信道和低SNR情况下依然可以获得良好的估计性能和远高于传统算法的估计精度,且适用于高铁等对频偏估计及修正精度和范围要求较高的场景。本文所提频偏估计算法拟应用于重庆市科技重大专项“5G 终端模拟器”。
3.2 频偏计算及修正

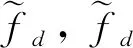
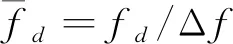


4 仿真及结果分析




5 结束语
