基于奇异谱分析与PSO优化SVM的混凝土坝变形监控模型

2020-12-10牛景太

水利水电科技进展 2020年6期

牛景太

(南昌工程学院水利与生态工程学院，江西南昌 330099)

我国现有大坝从数量与建设规模上均居世界首位，合理保障大坝安全运行，对有效发挥工程效益与保障地区稳定和居民生命财产安全具有重要意义[1-4]。变形是最能直观可靠地反映大坝综合运行性态的重要监测量，构建具有良好精度的变形监控模型可较好地反映大坝结构性能的演变特征，定量解读主要影响因素的作用和预测大坝运行情况，并依此对大坝性态加以评判[5-7]。

大坝变形主要由水位和温度变化引起的可逆变形以及筑坝材料性能随时间演变引起的不可逆变形组成。根据建模方法，大坝变形监控模型可分为统计模型、确定性模型与混合模型3类[8-10]。统计模型具有函数形式简单、计算高效的优点，因此得到了广泛的应用。近年来，伴随人工智能技术的发展，人工神经网络[11]、极限学习机[12-13]、混合蛙跳[14]、粒子群算法(partical swarm optimization，PSO)[15]、支持向量机(support vector machines, SVM)[16-18]、面板数据模型[19]等诸多算法被广泛应用于变形监控统计模型中，极大地推动了大坝变形监控模型的发展。其中，SVM基于风险最小化准则，具有良好的非线性分析能力，可有效地避免过拟合现象，故在变形监控模型中应用较为广泛[20-21]。针对核函数参数对SVM模型性能的影响，诸多学者对此开展了大量研究，例如，董明等[20]引入人工蜂群算法(artificial bee colony, ABC)对SVM参数进行寻优，并将构建的ABC-SVM模型应用于某混凝土双曲拱坝变形监控分析；谷艳昌等[21]采用遗传算法(GA)对SVM中核函数参数进行寻优，并将建立的GA-SVM大坝安全性态预测模型应用于土石坝坝体渗流压力分析中。受仪器量测精度与监测系统信息采集模块所伴有的固有噪声等影响，监测数据中难免存在一定的无法利用环境影响因素解释的随机性误差，为了最大化地消除固有噪声和随机误差等不利因素的干扰，小波分解[11,22]、经验模态分解[23]、奇异谱分析[24-25]等方法被广泛应用于大坝变形监测数据特征分解中。

鉴于实测变形中噪声成分对建模精度具有不利影响，本文采用奇异谱分析(singular spectrum analysis，SSA)对实测变形进行分解，并根据奇异值贡献率筛选表征混凝土坝变形的主成分对变形序列进行重构，以减小实测变形中噪声的影响。此外，考虑到SVM核函数参数对模型性能具有一定影响，采用PSO对SVM核函数参数寻求最优解。在上述研究的基础上，构建基于SSA与SVM的混凝土坝变形监控模型，并采用某混凝土拱坝垂线监测变形监控数据对建模方法的合理性和有效性进行了验证。

1 基于奇异谱分析的实测变形处理

变形测值的可靠性与稳定性是合理评判大坝运行性态的关键，而实际工程中，自动化监测数据受仪器精度、人为扰动等不确定性因素的影响，常蕴含一定的噪声成分[25]，该成分将导致建模精度的下降，为此，本文采用SSA方法对实测变形中噪声成分加以分离。SSA是一种多变量统计方法与概率理论相融合的非参数方法，该方法能有效地对某一时间序列中的趋势性成分、周期振荡成分和噪声成分加以分离[26-28]。SSA方法计算步骤如下。

步骤 1：计算轨迹矩阵X。对于含有N个样本的时间序列Y={y1,y2,…,yN}，有轨迹矩阵X

(1)

式中：L为窗口长度，L≤N/2；K=N-L+1。

步骤 2：奇异值分解。轨迹矩阵X的协方差矩阵S=XXT，计算XXT的特征值和特征向量，按特征值λ1、λ2、…、λL从大到小顺序排列相对应的特征向量U1、U2、…、UL。故轨迹矩阵X的奇异值分解写为

X=E1+E2+…+Ed

(2)

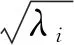
步骤 3：分组。根据Ei的下标i可将矩阵集合{E1,E2,…,Ed}划分为n个不相交的集合I1、I2、…、In，与之相应地，轨迹矩阵X可划分为n个矩阵：

X=XI1+XI2+…+XIn

(3)

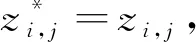
(4)

据此，原时间序列Y={y1,y2,…,yN}可被重构为

(5)

式中：r为时间序列重构所用的主成分个数，若r=L，则得到原时间序列。

2 基于SVM的变形监控模型

SVM是对数据进行分类与回归建模的方法[18,29-30]，其基本理念为寻找能正确划分训练样本的几何间隔最大的超平面。具体而言，对于某训练样本(x1,y1),(x2,y2),…,(xN,yN)∈(Rn×R)，通过非线性映射φ(x)将训练样本映射到一个高维空间中，构建线性优化函数来寻求最优线性分类面，该最优线性分类面可写为

f(x)=ω·φ(x)+b

(6)

式中：b为常数；ω为权值向量。

酸、甜、苦、咸和鲜为人类的5种基本味觉，产生的机理是溶解于水或唾液中的呈味成分刺激味蕾，信号传导至大脑皮层产生兴奋或味觉[22]。苦味的产生主要是多肽片段中疏水性氨基酸与人体苦味受体相互作用的结果。人的感官评定是目前鉴定苦味肽最常用、有效和直观的方法。因此通过感官分析，可为筛选苦味肽提供重要的依据。

根据结构风险最小化原则，ω与b可由下式求得：

(7)

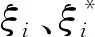
利用拉格朗日函数可将式(7)转化为

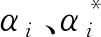
K(xi,xj)=exp[-‖xi-xj‖2/(2γ2)]

(9)

式中：γ为核半径。

进而可得到回归模型为

(10)

考虑到SVM模型中惩罚参数c与核半径γ对模型的泛化能力影响较大，为此，本文采用具有良好全局搜索能力的PSO对SVM模型中的参数c与γ进行寻优，具体的优化理论可见文献[30]。

3 混凝土坝变形监控模型

基于SSA与SVM模型基本理论，本文利用SSA良好的数据分析能力对混凝土坝变形监测数据中所蕴含的有效成分与噪声成分进行识别与筛除，进而对变形测值加以重构。在此基础上，为减小SVM核函数参数对模型性能的影响，采用PSO优化的SVM构建混凝土坝变形监控模型(SSA-PSO-SVM)，建模流程如图1所示。

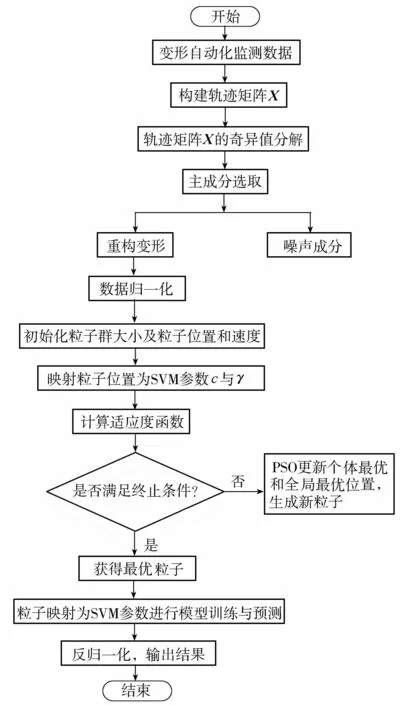
图1 SSA-PSO-SVM建模流程

混凝土坝变形监控模型[8]可表示为

δ=δH+δT+δθ=

(11)

其中θ=t/100

式中：δ为混凝土坝变形值；δH为变形水压分量；δT为变形温度分量；δθ为变形时效分量；H为上游水深；α0为常数；ai、b1i、b2i、c1、c2为统计系数；p为与坝型有关的系数，当坝型为重力坝时，p=3，坝型为拱坝时，p=4；t为建模日期至始测日的累计时间，d。

由式(11)可知，对于重力坝而言，监控模型中影响因子有9个，分别为H、H2、H3、sin(2πt/365)、sin(4πt/365)、cos(2πt/365)、cos(4πt/365)、θ、lnθ；对于拱坝而言，除此之外，其变形亦受H4的影响，共计10个影响因子。

为了评价混凝土坝变形监控模型的拟合与预报精度，采用平均绝对误差、均方误差和平均绝对百分误差来表征。

4 实例验证

某混凝土连拱坝坝顶长510 m，坝顶高程131.06 m，最大坝高75.9 m。采用正倒垂线监测坝体的水平位移，其中包括20条正垂线与3条倒垂线。利用两个正垂测点PL11与PL14在 2012年1月1日至2014年6月30日的自动化监测数据检验所建模型的预报精度，其中2012年1月1日至2014年5月31的监测数据用于模型训练，2014年6月1—30日的监测数据用于模型预报。相应监控时段内的环境量和测点变形分别如图2和图3所示。

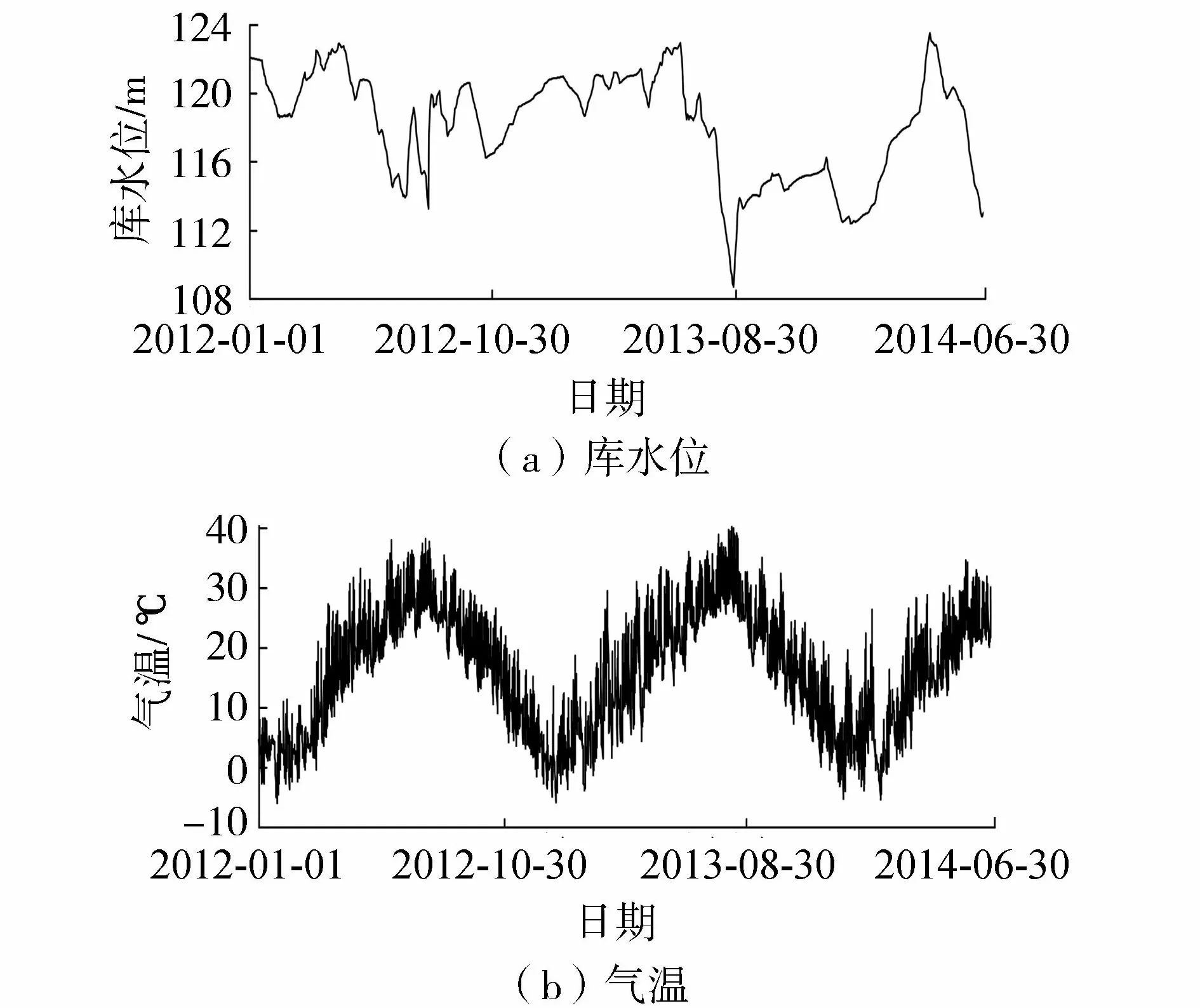
图2 环境量监测过程线

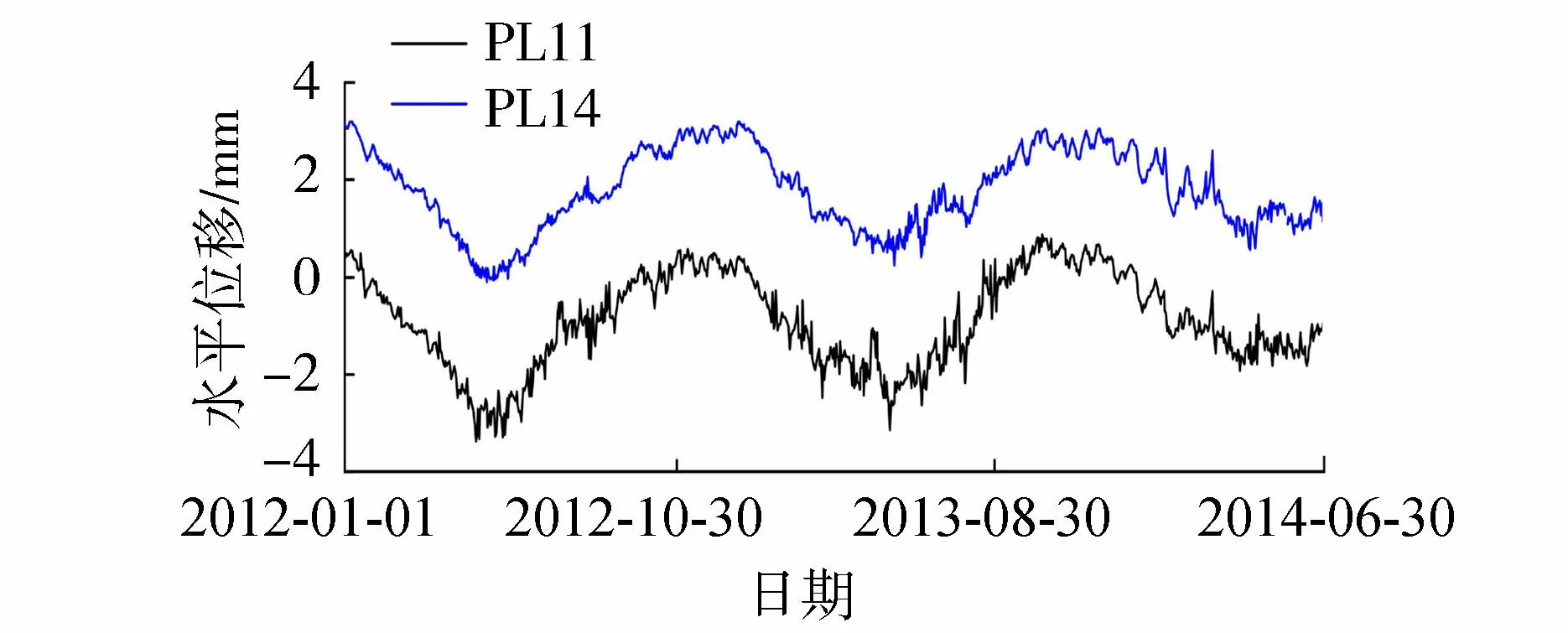
图3 水平位移实测过程线

由图3可知，两个测点测值的变化规律一致，且该坝变形主要受温度影响，温度下降，向下游方向变形增大，反之则减小；库水位的影响相对较小，库水位增大，向下游方向变形增大，反之则减小。以PL14测点测值为例，利用SSA对其测值中所蕴含的趋势性、周期性与噪声成分加以识别与分离。该方法需要确定的参数为窗口长度L，其一般取时间序列周期的整数倍，且小于样本长度的1/2，考虑到变形具有年周期特性，故取窗口长度为365 d。为保留尽可能多的数据信息，取累计贡献率达99%的主成分对实测变形进行重构。该测点经奇异谱分解得到的趋势性成分、周期性成分与噪声成分如图4所示，重构变形过程线如图5所示。

由图4可知，SSA分解得到的趋势性成分主要与时效有关，荷载变化对其有一定的影响，初步分析是因为温度的滞后效应引起的；周期性成分主要由库水位、温度等周期性变化的荷载引起的，具体表现为受温度影响引起年周期性变化与受库水位影响引起的波动变化的组合。由图5可见，利用趋势性成分与周期性成分重构的变形中噪声成分占比很小，除个别测值外，所分离的噪声成分多位于±0.2 mm范围内，重构变形有效保留了实测变形的数据特征，且该曲线更为平滑。构建变形预测模型时，经过PSO优化，得到SVM模型的最优参数c=1.46、γ=1.80，相应的拟合与预测结果如图6所示。

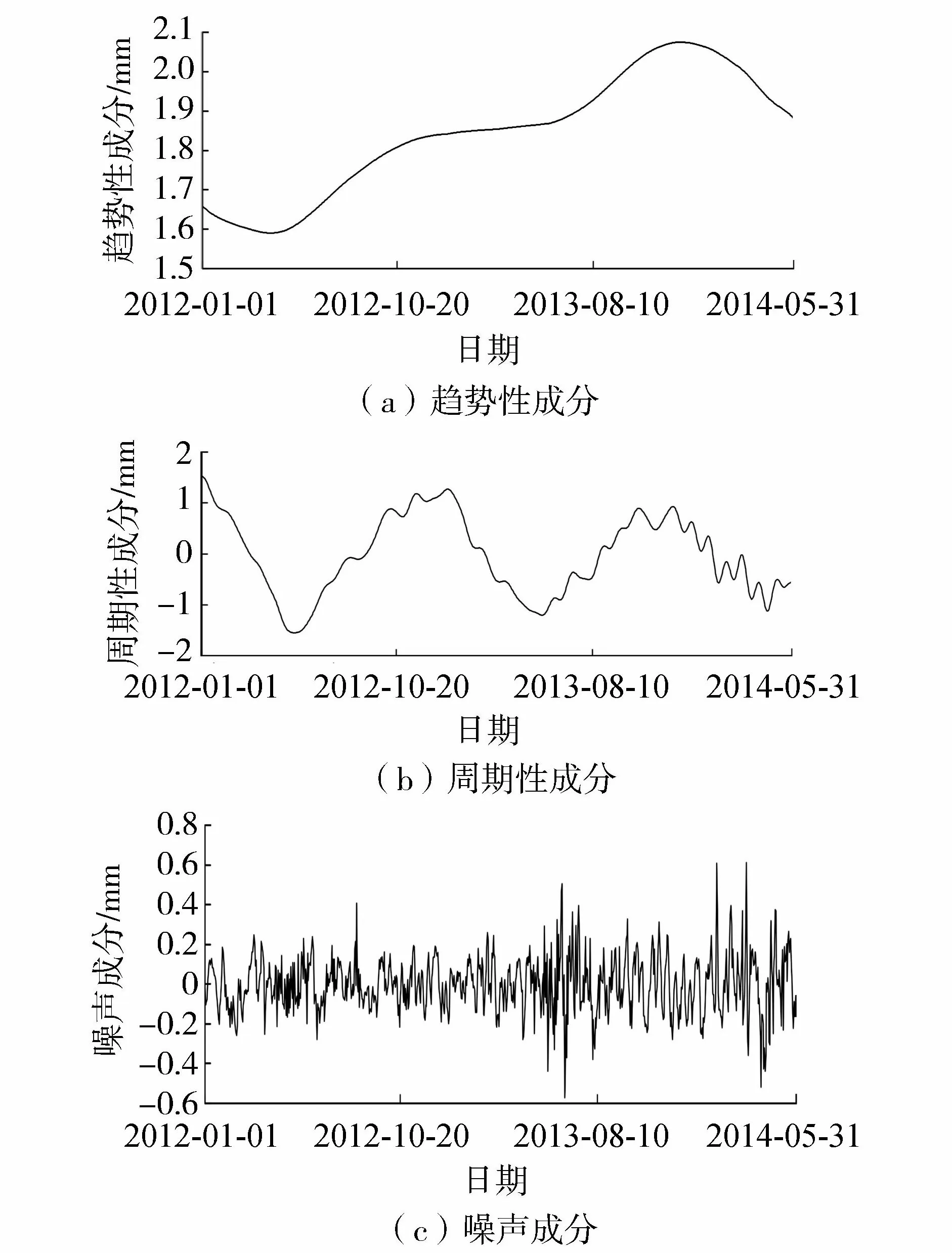
图4 基于奇异谱分析的PL14测点实测变形分解

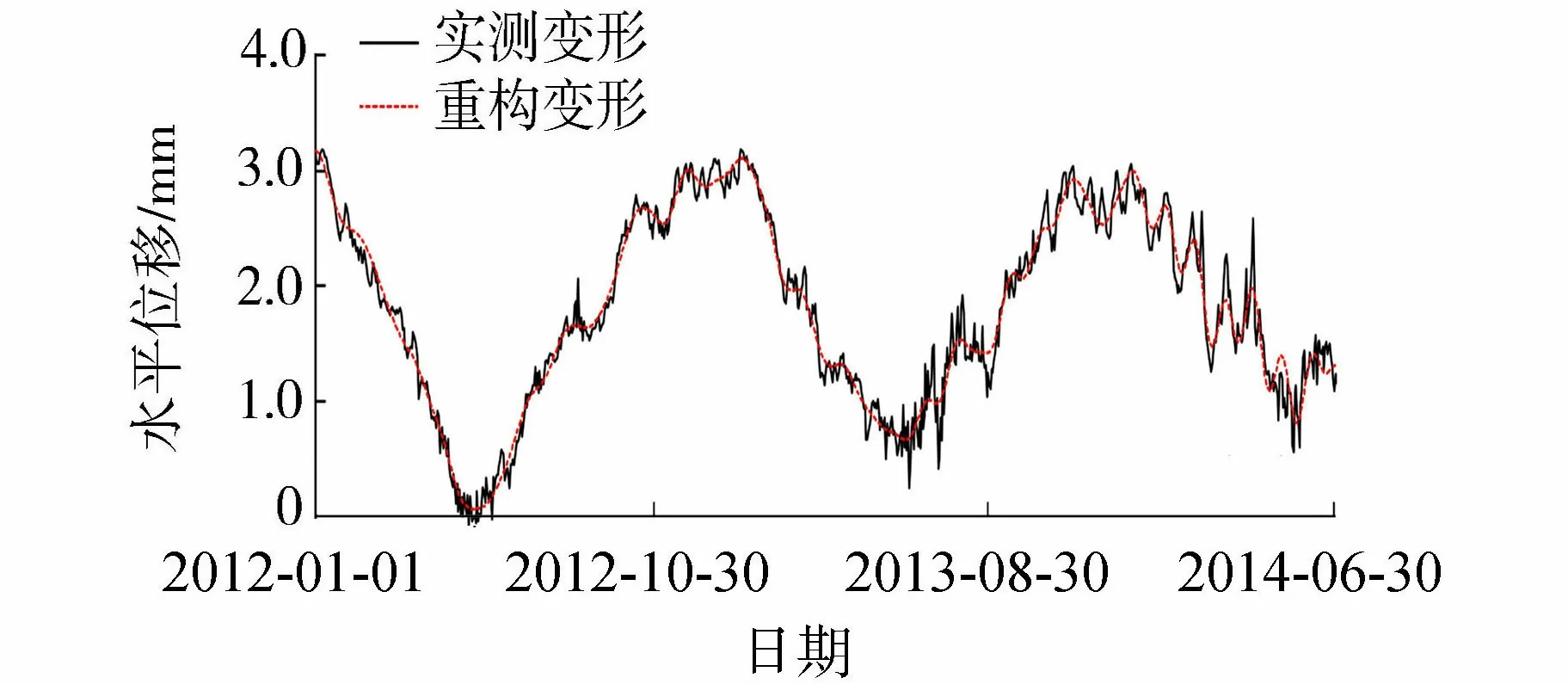
图5 PL14测点重构变形过程线

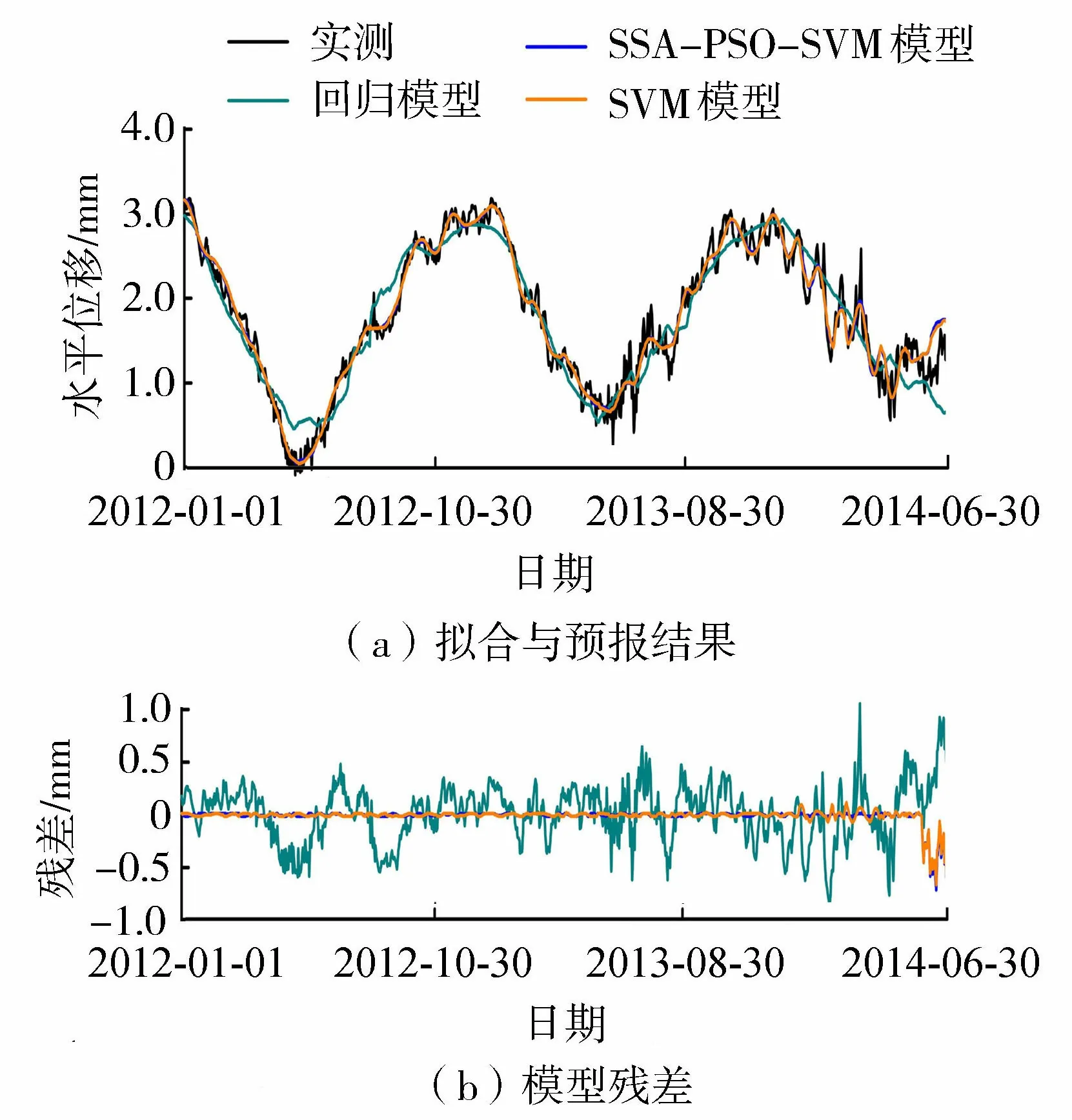
图6 PL14测点实测与监控模型拟合和预测结果

为验证所建SSA-PSO-SVM模型的有效性，利用逐步回归算法对实测变形构建的监控模型(回归模型)和采用SVM对重构变形构建的监控模型(SVM模型)作为对照。为进一步验证SSA-PSO-SVM模型的适用性，采用PL11测点测值进行建模，表1给出了3种模型拟合与预报的平均绝对误差、均方误差和平均绝对百分误差，图7为拟合与预测结果。

表1 统计指标

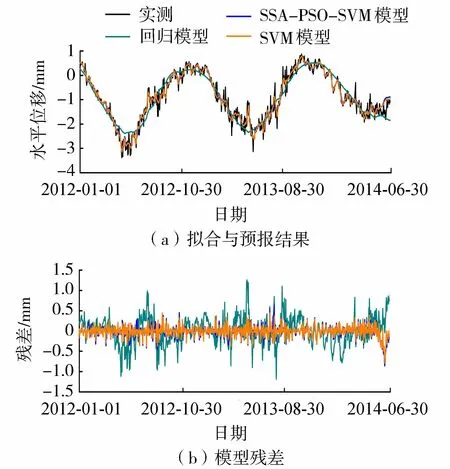
图7 PL11测点实测与监控模型拟合和预测结果

由图6、图7与表1可见，SSA-PSO-SVM模型具有良好的拟合与预测精度，其拟合或预测变形与实测变形较为接近，且模型残差相对较小；未经PSO优化的SVM模型较SSA-PSO-SVM模型拟合与预测精度稍差，而回归模型计算结果相对较差，仅能从实测变形的趋势上对其数据特征加以分析，不能有效地反映变形的短期动态波动特征。综上所述，SSA-PSO-SVM模型有效地挖掘了实测变形中的数据特征，减小了噪声扰动对建模精度的不利影响，有助于提升模型拟合与预报精度。