高混凝土重力坝坝踵裂缝水力劈裂特性分析
2020-12-10马泽锴
甘 磊,吴 健,马泽锴
(1.河海大学水利水电学院,江苏 南京 210098;2.水利部堤防安全与病害防治工程技术研究中心,河南 郑州 450003)
随着筑坝技术的快速发展,世界上已建成了许多高混凝土坝,其中不少已达200 m级,甚至300 m级,这些高坝常年在高水位条件下服役,大坝初始裂缝易起裂、扩展甚至贯穿,影响坝体整体性,威胁大坝安全[1]。国内外诸多学者开展了混凝土水力劈裂试验及机理研究,研究了混凝土裂缝张开速度对缝内水压分布的影响[2-4],探讨了不同缝内水压对裂缝扩展过程的影响[5-10],分析了不同裂缝形态或缝内水压分布形式对水力劈裂裂缝扩展过程的影响[11-14],讨论了不同位置、不同裂缝深度情况下混凝土重力坝裂缝稳定性[15]。在水力劈裂数值模拟方法方面,方修君等[16]基于扩展有限元法,模拟了重力坝地震开裂过程;董玉文等[17]采用扩展有限元法,开展了重力坝水力劈裂分析;Wang等[18]在董玉文等[17]的研究基础上,考虑了缝内水压与裂缝宽度的耦合关系,模拟了某重力坝水力劈裂演化过程;周维垣等[19-20]采用无单元伽辽金法模拟了拱坝的三维开裂过程和含孔洞岩体的水力劈裂裂缝扩展过程。
本文采用笔者建立的混凝土结构水力劈裂数值分析模型[21-23],模拟某高混凝土重力坝水力劈裂破坏过程,研究缝内水压作用对重力坝极限承载能力和裂缝扩展过程的影响,分析不同初始裂缝位置和初始裂缝深度下重力坝水力劈裂裂缝的稳定性,探讨缝内水压作用对重力坝建基面抗滑稳定安全的影响。
1 数值实现
1.1 缝内水压分布计算
针对高混凝土坝中存在的粗糙裂缝问题,沿裂缝长度方向取若干微段体,将整条裂缝视为由有限个单元构成的弥散裂缝,当微段体的长度足够短时,可将粗糙裂缝视为平行板之间的裂缝进行处理,且在裂隙面的两侧就近对应布设两排节点,每对垂直裂缝的节点之间的距离可以表征为该段裂缝的开度。在考虑裂纹中的水流流动方程时,利用差分原理,得到裂缝内水压力的差分形式,然后将裂缝处的节点概化为四边形单元,依次联立每个裂缝单元的缝内水压力计算式,采用迭代法求解裂缝内水压分布,使得本条裂缝其各节点的水压力之差最大值满足预设的精度要求即可,具体计算过程可参阅文献[23]。
1.2 水力劈裂扩展判据
数值模型考虑了渗透水压作用下复合型裂缝的应力强度因子,推导了不同应力状态下的水力劈裂裂缝开裂判据公式。裂缝面受拉时,其裂缝开裂判据公式[22]为
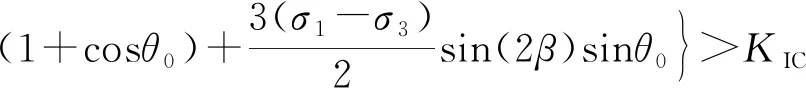
(1)
其中
式中:Kθ为裂缝尖端有效应力强度因子;θ0为开裂角;2l为初始裂缝长度;β为裂缝长轴方向与最大主应力夹角;P为作用于裂缝渗透水压;KIC为材料断裂韧度值;KⅠ、KⅡ分别为Ⅰ、Ⅱ型应力强度因子;σ1、σ3分别为单裂缝模型所受的竖向、水平向压应力。
裂缝面受压时,压剪应力状态下水力劈裂裂缝开裂判据公式[22]为
(2)
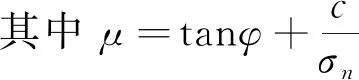
式中:φ为裂缝面的摩擦角;c为裂缝面的黏聚力;σn为裂缝面的法向压应力。
2 计算模型及参数
选定某高混凝土重力坝,沿坝踵和坝趾分别向上游、下游截取400 m作为计算模型上、下游边界,沿坝体建基面垂直往下截取400 m作为模型底边界,坝体断面如图1所示。坝基面高程设为0 m,坝高216.50 m,坝顶宽18.00 m,假定重力坝迎水面垂直,下游坝坡坡比为1∶0.73。将坝基和坝体作为整体进行计算分析,计算模型如图2所示,节点总数为5 855,裂缝尖端加密布置了100个节点。将坝踵定为模型坐标原点,以上游水平指向下游为x轴的正方向,竖直向上为y轴的正方向。
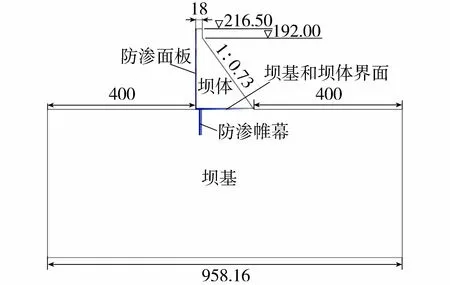
图1 坝体断面 (单位:m)

图2 大坝模型
计算考虑正常蓄水位210.00 m,对应下游水位40.00 m,假定坝体和坝基材料为各向同性弹性材料,在坝基与坝体交界处设置厚度为0.5 m的交界面,各分区材料的计算参数见表1。计算未考虑坝体排水的影响,主要考虑的载荷包括坝体自重,上、下游静水压力,裂缝内水压力和坝基自重。假定初始裂缝为水平裂缝,位于坝体上游面。坝基的上、下游边界设置为水平约束,底边界设为固定约束。
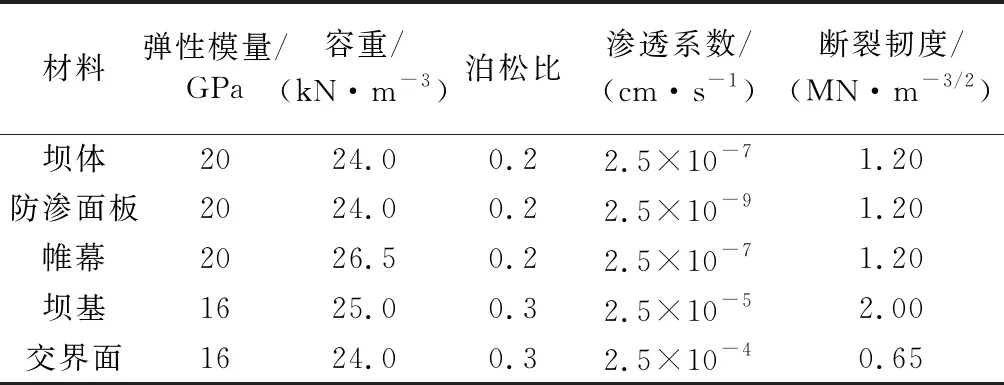
表1 各分区材料计算参数
3 结果与分析
3.1 缝内水压对裂缝扩展的影响
图3为考虑与不考虑缝内水压作用两种工况下裂缝扩展路径,两种工况下裂缝尖端有效应力强度因子随裂缝扩展过程的变化曲线如图4所示。由图3和图4可知,两种工况下裂缝均朝下游且向坝体底部扩展,不考虑缝内水压作用时,裂缝扩展6步后,裂缝尖端的有效应力强度因子降至0.78 MN/m3/2,低于混凝土材料的断裂韧度,裂缝不再扩展,对应的裂缝水平长度为2.328 m。考虑缝内水压作用时,裂缝尖端有效应力强度因子始终大于混凝土材料的断裂韧度,裂缝不断扩展,有效应力强度因子曲线存在拐点,在拐点处,有效应力强度因子骤增,呈现不稳定的扩展趋势,其裂缝水平长度为3.544 m。以上研究表明,缝内水压的存在会导致裂缝尖端有效应力强度因子增大,降低坝体裂缝的稳定性,影响坝体安全度。
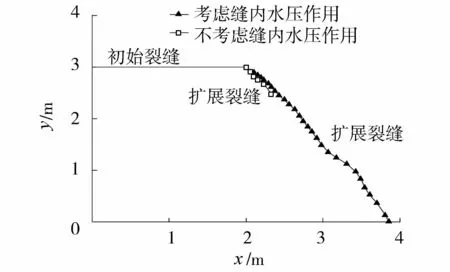
图3 裂缝扩展路径
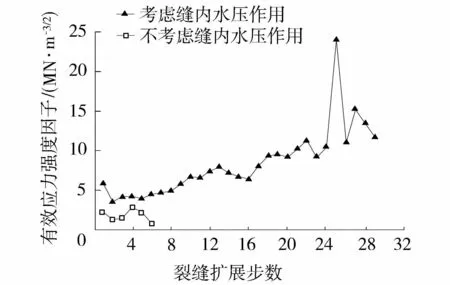
图4 裂缝尖端有效应力强度因子随裂缝扩展的变化
针对不同初始深度裂缝,对其裂缝面施加不同水压,保持水位恒定,分析该裂缝起裂时对应的临界上游水位,考虑缝内水压和不考虑缝内水压作用下的初始裂缝深度和临界上游水位关系曲线如图5所示。由图5可知,初始裂缝深度越小,裂缝起裂所需的临界上游水位值越大,考虑缝内水压力作用时,极限荷载受初始裂缝深度的影响较大;不考虑缝内水压作用时,临界上游水位-初始裂缝深度曲线较平缓,初始裂缝深度小于2.0 m时,坝体的极限承载水头为241.0~243.0 m,约为坝高的1.12倍;考虑缝内水压作用时坝体的极限承载能力较未考虑缝内水压情况显著降低,当初始裂缝距离坝踵的高度为3.0 m,裂缝深度为2.0 m时,缝内水压作用下坝体极限承载能力比不考虑缝内水压情况下降17.6%,随着裂缝深度的不断增大,坝体承载能力降低的速率减缓。

图5 临界上游水位-初始裂缝深度曲线
在不同缝内水压作用情况下,裂缝均向坝体底部和下游侧扩展,缝内水压力越大,裂缝开裂深度越大,当缝内水压增至2.05 MPa时,裂缝转变为不稳定状态,不断扩展至坝体破坏[22]。
3.2 裂缝位置对裂缝稳定性的影响
假定初始裂缝为水平裂缝,位于坝体上游面,裂缝深度为2 m,考虑初始裂缝距离坝踵的高度ha分别为0 m、3 m、5 m、7m和10 m 5种方案,分析不同初始裂缝位置对裂缝稳定性的影响。不同位置初始裂缝的断裂参数见表2。由表2可知,当初始裂缝深度为2 m时,ha越小,即初始裂缝越靠近坝踵,缝内水压对裂缝的劈裂作用越显著,裂缝就越不稳定。考虑缝内水压作用时,ha≤ 5 m的裂缝处于拉剪断裂模式,其裂缝尖端有效应力强度因子一直大于材料断裂韧度值,裂缝一直扩展至坝体发生失稳破坏为止,裂缝不稳定;当ha增至 7 m后,裂缝受力状况由拉剪转化为压剪,裂缝处于稳定状态。
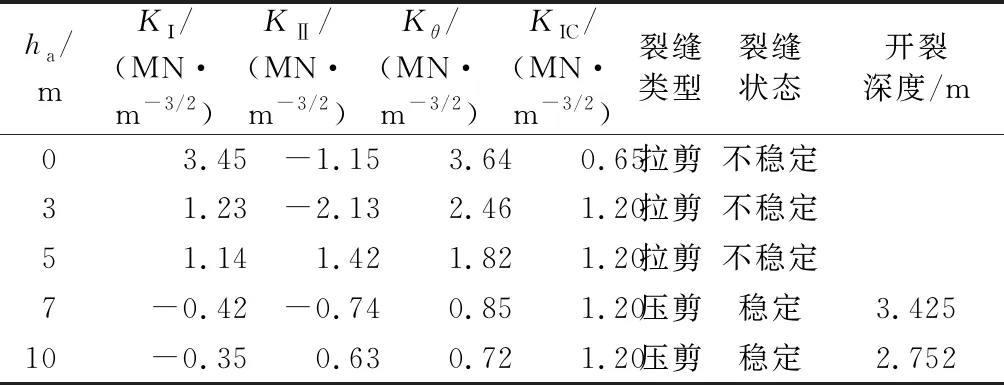
表2 不同位置初始裂缝的断裂参数
3.3 裂缝深度对坝体建基面应力分布的影响
假定初始裂缝在坝踵位置,对初始裂缝深度a0分别为0 m、5 m、10 m、20 m和30 m 5种情况下建基面上的垂直正应力和切向剪应力进行分析,不同初始裂缝深度下坝体沿建基面上的应力分布如图6所示。
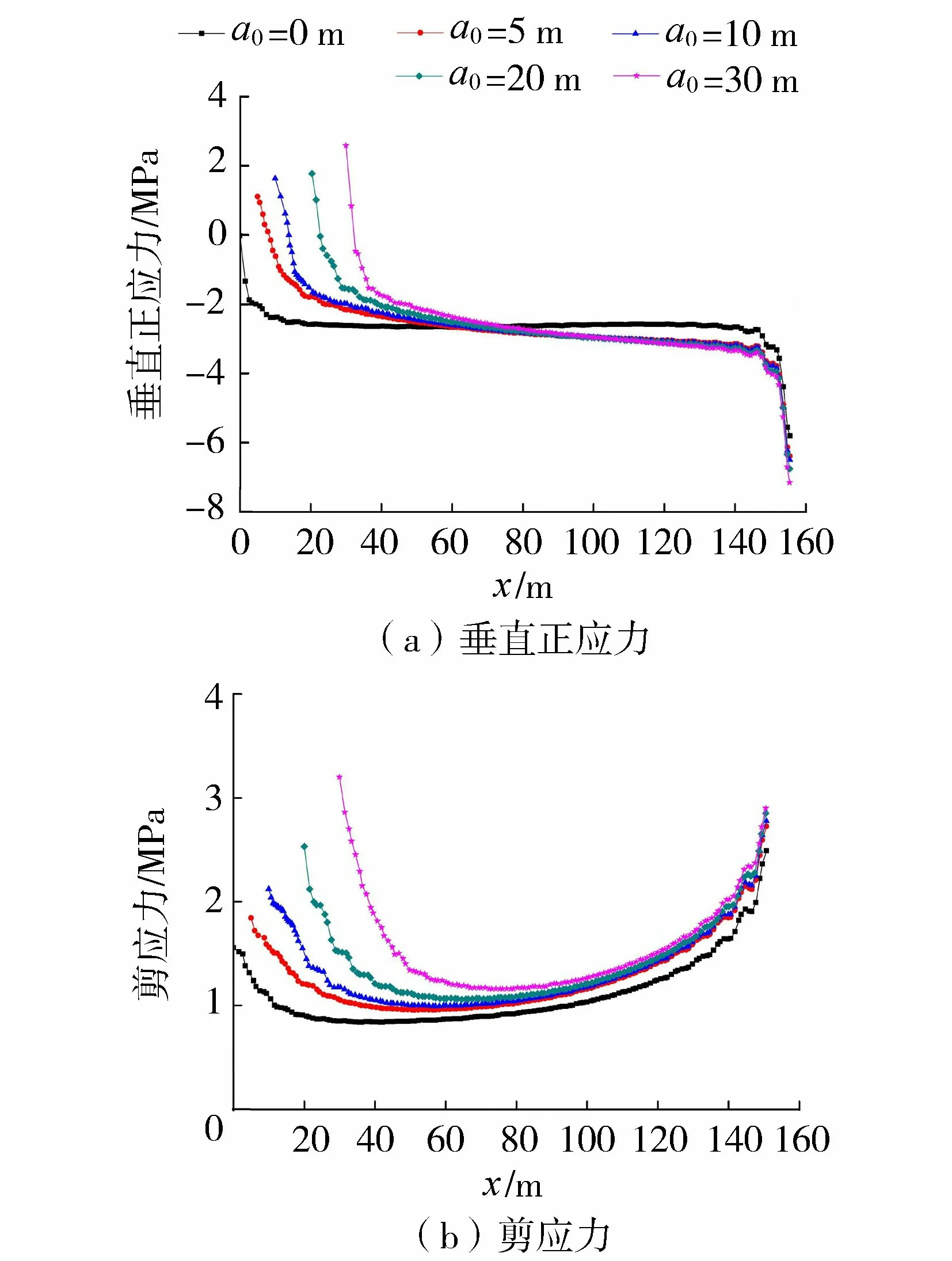
图6 不同初始裂缝深度下坝体沿建基面的应力分布
由图6可知,裂缝的存在使得坝踵附近较小区域存在拉应力,而坝体沿建基面仍基本上处于受压状态;裂缝的存在对裂缝尖端附近区域应力影响较大,而对离裂缝较远的区域应力影响很小,具有一定的局部效应;随着初始裂缝深度的增大,建基面上裂缝尖端附近的应力变化较为明显,远离裂缝的下游侧应力变化较小。
3.4 坝体建基面抗滑稳定性
基于垂直正应力和剪应力分布结果,采用如下公式[24]计算坝体沿建基面的抗滑稳定安全系数K:
(3)
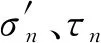
考虑与不考虑缝内水压作用两种数值方案下,裂缝均沿着坝体和坝基的交界面不断扩展,坝体建基面抗滑稳定安全系数随裂缝深度的变化关系如图7所示。由图7可知,随着裂缝深度的不断增大,两种数值方案下的坝体抗滑稳定安全系数均下降;在裂缝深度相同的情况下,与不考虑缝内水压作用相比,考虑缝内水压作用计算出的抗滑稳定安全系数偏小,裂缝深度为30 m情况下减小了29.3%;不考虑缝内水压作用时,无裂缝情况该坝的抗滑稳定安全系数为4.079,裂缝深度为10 m情况下为3.952,减小了3.1%;考虑缝内水压时,坝体抗滑稳定安全系数从无裂缝情况下的4.079减小至裂缝深度30 m情况下的3.056,减小了25.1%,说明在缝内水压作用下,随裂缝深度的增大,坝体的抗滑稳定安全系数的下降速率较快,约为未考虑缝内水压情况的8倍。
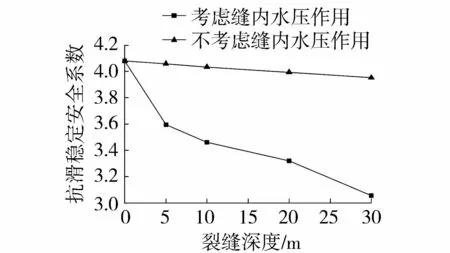
图7 坝体建基面抗滑安全系数随裂缝深度的变化
4 结 论
a. 当初始水平裂缝距离坝踵的高度为3.0 m,裂缝深度为2.0 m时,考虑缝内水压作用下坝体极限承载能力较未考虑缝内水压情况降低了17.6%,缝内水压作用下坝体极限承载能力显著降低,且随着裂缝深度的增大,坝体承载能力降低速率减缓。
b. 当初始水平裂缝深度为2.0 m,裂缝距离坝踵的高度小于等于5.0 m时,坝体裂缝处于拉剪断裂模式,裂缝呈不稳定扩展趋势,当初始裂缝距离坝踵的高度增至7 m后,裂缝转变为稳定状态。
c. 裂缝的存在使得坝踵附近较小区域存在拉应力,对裂缝尖端附近区域应力影响较大,存在一定局部效应,且随着初始裂缝深度的增大,建基面上裂缝尖端附近的应力变化较为明显。
d. 初始水平裂缝位于坝踵位置时,考虑缝内水压作用下坝基面抗滑稳定安全系数下降明显,下降速率为未考虑缝内水压情况的8倍,缝内水压作用对重力坝建基面抗滑稳定不利。
