基于WMLES方法的复式断面明渠三维紊流数值模拟

曾 诚，丁少伟，周 婕，王玲玲，陈 辰

(1.河海大学水利水电学院，江苏 南京 210098； 2.河海大学力学与材料学院，江苏 南京 210098)

在平原地区，天然河道和人工渠道断面大多为复式结构，包括主槽和滩地。平时水流主要集中在主槽中流动，汛期水流漫过滩地，主槽和滩地共同过流，形成复式断面流动。由于主槽和滩地上水流之间较大的流速差异，导致在滩槽交界处出现较大的动量交换，使得内部水流结构体现出三维流动特征。在垂直于主流的横断面上，出现由紊流驱动的二次流，引起横向的物质输运、岸坡冲刷等问题。因此，研究复式断面明渠紊流的三维流动特征，对于河道行洪断面设计和加固具有重要意义。

许多学者对复式断面明渠滩槽交界处二次流和动量交换机理进行了试验和理论研究。Rajaratnam等[1]、Myers[2]、Wormleaton等[3]、Tominaga等[4]、Shiono等[5]、Sanjou等[6]先后对复式断面明渠紊流进行了试验测量，对主槽和滩地间的动量交换机理进行了研究。他们的研究结果表明滩槽交界面上的切应力比固体边界上的平均剪切应力大许多倍，证明复式断面明渠流动中横向动量交换强于垂向动量交换，在流动中占据主导地位。

在复式断面明渠流的数值模拟研究方面，大量成果均基于雷诺时均方程的涡黏性紊流模型。Sofialidis等[7]发现当相对水深比和雷诺数较小时，非线性k-ω模型比非线性k-ε模型有更好的表现。林斌良等[8]采用非线性k-ε模型和雷诺应力模型(Reynolds stress model，RSM)对复式断面明渠紊流进行了模拟研究，结果表明两种模型均能较好地模拟复式断面明渠三维紊流结构，RSM得出的主流速分布更接近试验结果，两种模型得出的雷诺应力分布趋势与试验结果一致，但在数值上偏大较多。梁爱国等[9-11]采用RSM对复式断面弯道明渠三维流场结构进行了模拟研究，揭示了水深比和弯转角度对流场中漩涡结构的影响。Cater等[12-13]运用大涡模拟(LES)方法对非对称矩形复式断面明渠进行了模拟，得到了详细的流场信息，且精度较高。许栋等[14]采用LES方法对复式断面明渠水流进行了数值模拟研究，揭示了水深比和雷诺数对其紊流结构的影响。

前人的研究结果[12-14]表明，LES方法对于复式断面明渠流动具有较好的模拟精度，但是在边界层内需要足够细密的网格来保证最小尺度的漩涡结构能够被捕捉到。同时，对于复式断面明渠流问题而言，由于垂直方向上存在两个边界层区域(滩地底面和主槽底面)，导致利用LES方法对该类问题进行模拟研究的计算成本很高。Shur等[15]提出了一种壁面建模的大涡模拟(wall-modeled LES，WMLES)方法，克服了传统LES方法在模拟高雷诺数下近壁面紊流时要求非常精细网格尺度的问题。与传统LES方法相比，WMLES无须加密边界层中的网格，可节约计算成本。目前，这种方法已经越来越多地应用于数值模拟中[16-17]。本文采用WMLES方法对复式断面明渠流动进行模拟研究，并将计算得到的主流速、二次流、床面切应力、紊动强度、紊动能及雷诺应力与已有的试验测量值[4]和LES模拟结果[12-13]进行对比分析，以验证WMLES方法对于此类流动问题的适用性和可靠性。

1 数学模型

1.1 控制方程

连续方程和动量方程的过滤形式如下：

(1)

(2)

由滤波造成的亚格子应力是未知的，须通过建模进行求解。本文采用Boussinesq假设对亚格子应力进行计算：

(3)

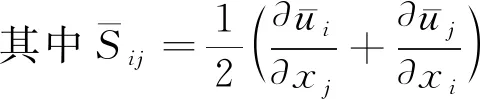
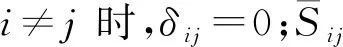
νt=min[(κdw)2,(CsmagΔ)2]·

|S-Ω|{1-exp[-(y+/25)3]}

(4)

式中：dw为计算点与壁面间距；S为应变速率；Ω为涡量；参数κ=0.41，Csmag=0.2；Δ为滤波尺寸；y+为垂直壁面的无量纲距离。传统LES方法中，滤波尺寸通常通过下式进行计算：

Δ=(ΔxΔyΔz)1/3

(5)

式中：Δx、Δy、Δz分别为沿x、y、z轴方向的网格尺寸。这种计算方法适用于各项同性或者近似各向同性网格，导致计算网格在单元数量上过于密集，进而导致计算成本提高。与传统的LES方法相比，WMLES方法在计算滤波尺寸时引入了壁面阻尼函数项(如式(6)所示)，使得该方法适用于各项异性网格，从而降低网格数量，提高计算效率。

Δ=min[max(Cwdw,Cwhmax,hwn),hmax]

(6)

式中：hwn为沿壁面法向的网格尺度；hmax为壁面网格的最大尺度；Cw为常数，取为0.15。

1.2 数值方法与边界条件

为保证流场充分发展，选取SSTk-ω计算的稳态场作为WMLES计算的初始流场。离散格式选取具有三阶精度的QUICK格式，压力场和速度场的解耦计算采用PISO算法。

在入口和出口边界上采用周期性边界条件，自由水面边界采用刚盖假定，固体壁面为无滑移边界。

2 计算域及网格划分

选取Tominaga等[4]的物理模型试验测量数据进行模型验证和分析。试验在长为12.5 m，主槽宽度b=0.2 m，河道总宽度B=0.4 m的复式断面水槽中进行，采用激光多普勒测速仪测量流速。选取水深比hr=0.5的工况进行模拟(hr=h/H，其中h为滩地水深，H为主槽水深)，主槽水深和滩地水深分别为0.08 m和0.04 m，平均流速Um为0.349 m/s，雷诺数为54 500，摩阻流速为0.016 4 m/s。图1为数值模拟计算区域示意图，x、y、z分别为流向、展向和垂向坐标。数学模型的计算域大小为10H×5H×H(x×y×z，下同)。计算中为了便于结果处理与分析，采用主槽水深H对坐标系无量纲化。水槽沿x向坡度S0=6.397×10-4。

图1 计算区域和尺寸

采用六面体网格对计算区域进行剖分，在x、y、z方向均采用均匀结构化正交网格，未对边界层进行加密。网格划分与数值模拟的精度及计算结果的收敛性密切相关，因此本文选取3组不同精度的网格进行网格无关性验证，工况C1、C2、C3网格数量分别为128×100×64、160×200×80、 200×400×100。3组不同网格精度工况的流向时均流速U沿横断面分布如图2所示，图中以平均速度Um对U进行无量纲化。由图2可知，工况C1由于网格精度不足，与另外两组工况计算结果差距较大。工况C2和C3流向时均流速U的分布基本一致，误差在5%范围以内。说明更密的网格对模型的计算结果没有显著的影响，但是工况C3的计算时间远远超过工况C2的计算时间。为了节约计算成本，最终选取工况C2的网格划分方案(160×200×80)作为本次计算的网格方案。Cater等[12]，Xie等[13]也运用LES方法对Tominaga等[4]的物理模型试验工况进行验证分析，他们采用的网格数量分别为500×320×128和192×384×96，分别是本次模拟网格数的8倍和2.7倍。

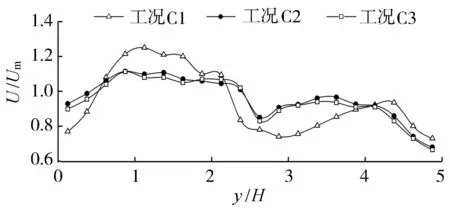
图2 不同网格精度下流向(x方向)时均流速分布

3 计算结果与分析

计算约60个流动周期(一个流动周期T=10H/Um)后流场达到充分发展状态，开始统计流场的时均流动特性，统计时间为50个流动周期。U、V、W分别为x、y、z方向的时均流速。为对WMLES方法在复式断面明渠流动模拟中的表现进行全面的评价，将模拟计算结果与Tominaga等[4]的试验测量数据，Xie等[13]基于动态亚格子模型的大涡模拟结果和Cater等[12]基于Smagorinsky模型的大涡模拟结果进行比较。

3.1 主流速等值线

以最大主流速Umax对主流速进行无量纲化，计算得到的主流速等值线分布如图3(d)所示。计算得到的最大主流速出现在主槽中心z/H=0.67附近。由图3可以看出WMLES计算结果与Tominaga等[4]的实测值吻合。在主槽与滩地交界处，由于二次流的影响，主流速等值线向主槽侧的自由水面凸起。同时可以观察到主流速在接近自由水面的位置速度减小的现象。在断面上由于强烈的二次流动，涡体将动量较高的水体向水槽两边输运，导致主流速等值线在拐角附近发生较大程度的弯曲。在自由水面附近靠近壁面处受壁面的影响，主流速等值线也出现较大程度的弯曲。与Cater等[12-13]的模拟结果相比，WMLES模拟的断面主流速在滩槽交界面处与实测值更接近。

图3 横断面主流速U/Umax分布

3.2 二次流

图4(d)是通过WMLES计算得到的断面流速矢量图，图中V、W已通过最大主流速Umax进行无量纲化。Prandtl根据形成原因将二次流分为两类：第一类Prandtl二次流常产生在弯曲河道中，离心力的作用使水流偏离主流方向，此类二次流强度较大；第二类Prandtl二次流常发生在复式断面河道边角附近，由于雷诺应力的各向异性导致水流偏离主流方向，此类二次流强度相对较小。与试验中观察到的现象一致，图4中可以看出在滩地与主槽交界处产生较强的二次流，存在一对旋转方向相反的涡延伸至自由水面，靠近主槽的涡称为深槽涡，靠近滩地的涡称为浅滩涡。另外，计算结果显示在主槽靠近壁面处有一漩涡，称为自由水面涡。自由水面涡的影响范围超过主槽宽度的一半，它将缓慢流动的流体从侧壁附近输送到水槽的中心部分，这也是主流速最大值出现在自由水面以下的原因之一。与试验测量结果[4]和前人计算结果[12-13]相比，WMLES方法模拟计算得到的横断面漩涡结构在位置和方向上都较为一致。

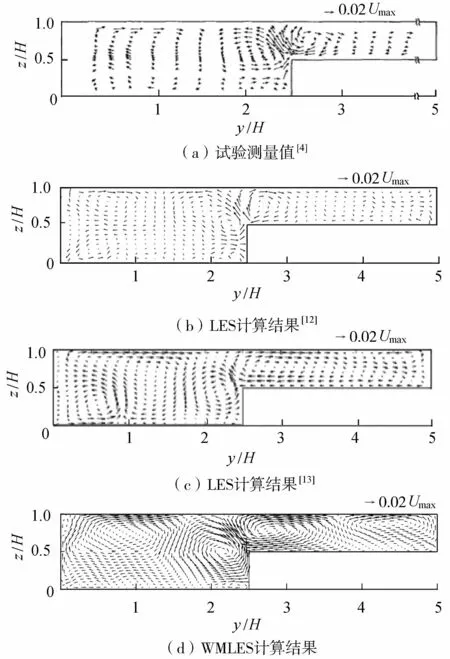
图4 横断面流速矢量

3.3 床面切应力

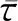
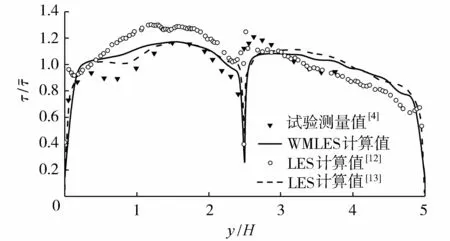
图5 横断面床面切应力分布

3.4 紊动强度

水流流速的脉动强弱程度通常可以由紊动强度来反映，紊动强度用脉动流速的均方根来表示：

(7)

(8)

式中：urms、vrms、wrms分别为流向、展向和垂向紊动强度。

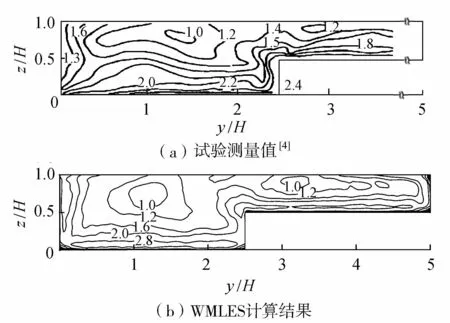
图6 流向紊动强度urms/uτ分布

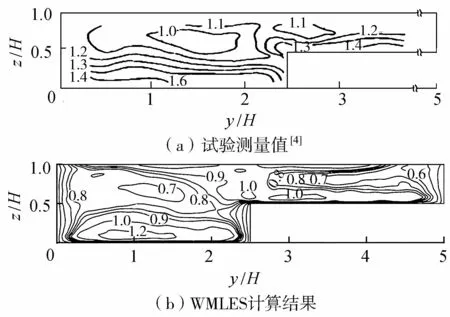
图7 展向紊动强度vrms/uτ分布

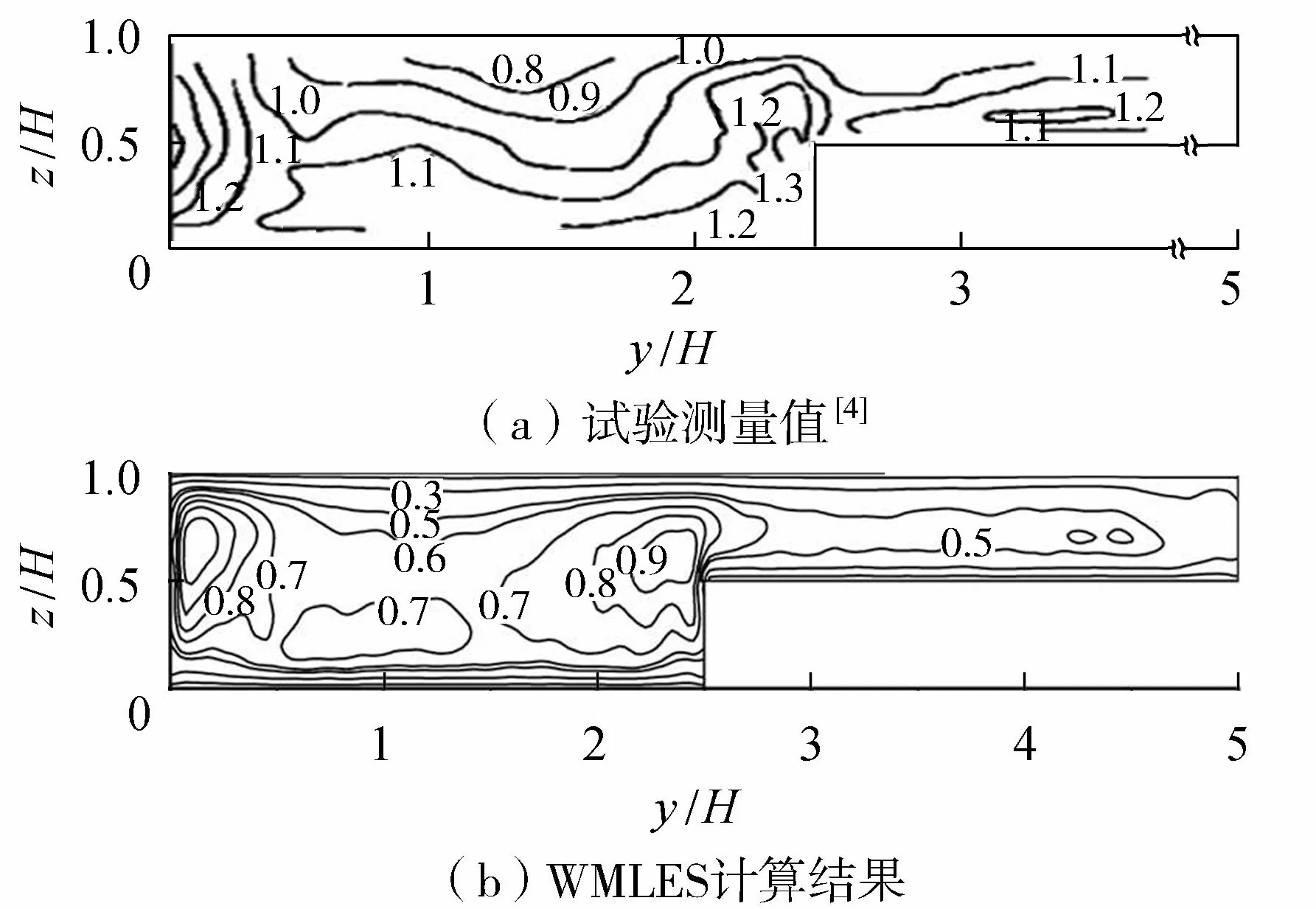
图8 垂向紊动强度wrms/uτ分布

图9 紊动能分布

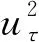
3.5 雷诺应力

图10 雷诺应力断面分布

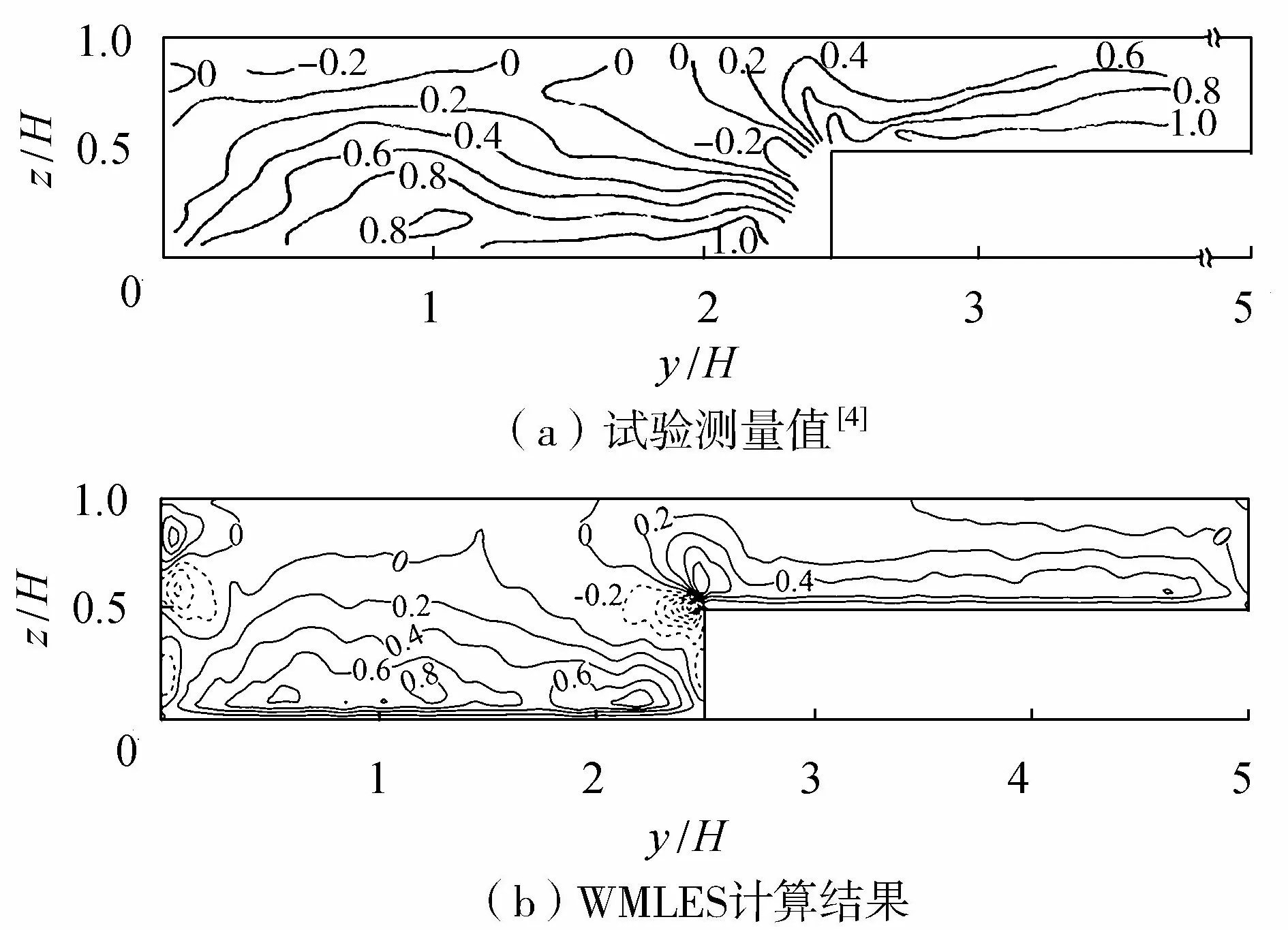
图11 雷诺应力断面分布

由图10可知，-〈u′v′〉的值与速度梯度∂U/∂y有关，代表了滩槽交界面处动量交换的强度。在主槽内-〈u′v′〉的绝对值出现最大值，同时可以发现在滩槽交界的拐角处y/H>2.5的部分区域-〈u′v′〉的值为正值。表明动量交换在主槽内最强烈，水体在滩地靠近床面附近动量从主槽向滩地输运。在主槽靠近壁面侧-〈u′v′〉的值逐渐增大，这与该处存在自由表面涡有关。

由图11(b)可知，在主槽内靠近床面-〈u′w′〉的值逐渐增大，主槽与滩地交界处的左侧出现负值，这与试验结果是一致的。在滩地内-〈u′w′〉模拟值与试验测量值相比偏小，两者的变化规律一致。

4 结 语

本文利用WMLES方法对水深比为0.5的复式断面明渠水流进行三维大涡模拟研究。与传统LES方法相比，WMLES无须在边界层内对网格加密，很大程度上降低了计算成本。就本文算例而言，与Cater等[12]和Xie等[13]的LES数值模型相比，利用WMLES方法使得计算网格数量分别减少到其网格数量的1/3和1/8。WMLES计算结果与试验测量值[4]和LES计算结果[12-13]的比较表明,WMLES能够准确模拟平均流速、床面切应力、紊动强度、紊动能和雷诺应力分布，并且能够准确模拟出断面内的二次漩涡结构。本文验证了WMLES方法对于复式断面明渠流动模拟问题的适用性和可靠性，为后续研究打下基础。