标准型异形椭圆断面正常水深和临界水深计算
2020-12-10武周虎祝帅举
武周虎, 王 瑜, 祝帅举,2
(1.青岛理工大学环境与市政工程学院,山东 青岛 266033;2.河南省城乡规划设计研究总院有限公司,河南 郑州 450044)
在水利、水电、调水、灌溉等穿越工程的输水中,较多采用无压隧洞形式,其正常水深和临界水深是无压隧洞的重要设计参数。对于现行的圆形、马蹄形、蛋形等无压隧洞断面形状,正常水深和临界水深的计算大多涉及超越方程,无法求得解析解。近年来,在圆形[1-2]、马蹄形[3-4]、蛋形[5-6]等无压隧洞断面正常水深和临界水深的直接求解研究中,较多采用迭代法、函数替代拟合法等,得到了一系列精度较高的直接计算公式。
马蹄形、蛋形等无压隧洞断面的内轮廓线是由圆心位置、半径不同的多段圆弧相切或相交组成。以四圆弧马蹄形断面为例,就有半径r1、r2、r3和切点高度h1、h2(或圆心角)共5个独立变量,各变量之间的转换关系复杂,水力要素计算公式的分区表达不可避免,导致在正常水深和临界水深的计算过程中,需先以分界流量或者充满度的范围来界定各分区,通用性不强[3-6]。在实际工程应用中,各水深计算公式的选择比较困惑。武周虎等[7-8]推导的宽阔河流中心稳定点源条件下保守物质的等浓度线方程,可作为一种新型Wu’s二参数曲线(以下定义为异形椭圆)水工隧洞断面内轮廓线方程。该断面形状只有2个独立变量,曲线完整且连续光滑,克服了马蹄形、蛋形等断面曲线的分段组合及水力要素公式的分区问题。从结构特征上来讲,异形椭圆断面曲线可以克服马蹄形、蛋形等断面曲线在相交或相切点处一阶或二阶导数不连续、曲率突变和应力集中现象。因此,异形椭圆在水工隧洞、交通隧道等工程中具有非常广泛的工程应用价值[9-11]。
本文基于无压隧洞最大宽度W与最大高度H相等的标准型异形椭圆断面形式,在系统归纳标准型异形椭圆断面水力要素计算公式的基础上,根据明渠均匀流和临界流基本方程,引入量纲一参数和采用曲线优化拟合的分析方法,结合标准型异形椭圆断面正常水深和临界水深的变化特征,在工程应用范围内,提出标准型异形椭圆断面正常水深和临界水深的直接计算公式,并进行误差和算例分析。
1 标准型异形椭圆断面的水力要素
1.1 标准型异形椭圆断面曲线方程
异形椭圆断面曲线是基于宽阔河流中心稳定点源条件下,保守物质浓度分布的等浓度线方程推演而来的[7-8],是由一个独立两参数方程表征的完整连续光滑曲线,其Wu’s曲线方程[9-10]为
(1)
式中:z为自隧洞断面底部中点向上的垂向坐标,即表征断面的高度坐标,取值范围为0≤z≤H;y为垂直于z轴的横向坐标,即表征断面的宽度坐标,取值范围为-W/2≤y≤W/2。异形椭圆断面最大宽度处相应的垂向坐标为zw=H/e≈0.368H。
定义异形椭圆的压缩系数为非对称轴y方向的宽度与对称轴z方向的高度之比,以θ=W/H表示。据此,将异形椭圆的形状分类为:当压缩系数θ=1时,异形椭圆的宽度等于高度,称为标准型;当0<θ<1时,异形椭圆的宽度小于高度,称为H型(高瘦型);当θ>1时,异形椭圆的宽度大于高度,称为W型(宽胖型)。对于标准型异形椭圆断面,为便于分析讨论,定义断面参数H,则标准型异形椭圆断面曲线方程为
(2)
由式(2)绘制的标准型异形椭圆断面及其特征尺度如图1所示。
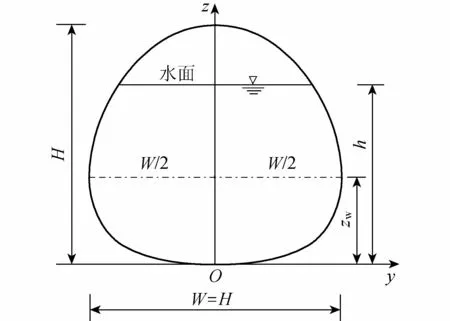
图1 标准型异形椭圆断面及其特征尺度示意图

1.2 标准型异形椭圆断面的水力要素计算
在无压隧洞内任一水深h处,其充满度(即相对水深)α=h/H,结合压缩系数θ=1的标准型异形椭圆断面的参数H,对文献[10]中异形椭圆断面的水力计算公式进行简化整理,可得到标准型异形椭圆断面的水力要素计算公式。
a. 水面宽度。在式(2)中,令z=h,则水深h相应充满度α所对应的水面宽度B的表达式为
(3)
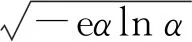
b. 过水断面面积。由图1可知,标准型异形椭圆断面的过水断面面积为水面线与其下部断面曲线所包围部分的面积。在z∈[0,h]区间上,对式(2)变形后y=f(z)函数的2倍求定积分,令z/H=ζ,其积分上限变为充满度α,则过水断面面积A的表达式为
(4)

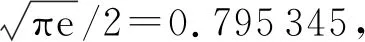
c. 湿周。由图1可知,标准型异形椭圆断面的湿周为水面线下部断面轮廓曲线的弧长。在z∈[0,h]区间上,对标准形异形椭圆断面曲线方程y=f(z)函数求2倍弧长定积分,则过水断面湿周的表达式为
T(α)H
(5)

式中:y′为y=f(z)的一阶导数;T为标准型异形椭圆过水断面的湿周系数。当α=1时,由MATLAB数值积分计算结果,T(1)=3.191 244为断面最大湿周系数,相应的湿周为隧洞满管流断面的周长L。
d. 水力半径。水力半径为过水断面面积与湿周之比,由式(4)与式(5)可得
(6)

式中:R′为标准型异形椭圆过水断面水力半径与断面参数H的比值,即相对水力半径。
2 标准型异形椭圆断面的正常水深
2.1 明渠均匀流基本方程
明渠均匀流水深称为正常水深,是明渠水面线分析计算的基础参数,也是无压隧洞设计的重要参数。明渠均匀流基本方程[12]为
(7)
式中:Q为输水流量,m3/s;i为底坡;n为糙率。
将式(4)和式(5)代入式(7),整理可得到关于标准型异形椭圆断面正常水深的隐函数表达式:
(8)
式中两个等号中间的表达式为充满度或正常水深的隐含关系式。将式(8)右边的表达式设为标准型异形椭圆断面的正常水深模数ηn:
(9)
由式(8)可知,正常水深模数ηn与充满度α之间存在隐函数关系ηn=f(α)。可根据已知的隧洞断面特性参数及水流条件(糙率n、底坡i、断面参数H和流量Q等)由式(9)求得ηn,而式(8)两个等号中间关于α的表达式包含对数、积分和指数运算,因此,仍然无法根据正常水深模数直接求得与其相应的充满度解析解。
2.2 正常水深的简化计算
为解决充满度解析解求解问题,获得标准型异形椭圆断面正常水深的直接计算公式,采用函数替代法,将求解正常水深的问题转化为寻求量纲一参数之间的近似函数关系。首先,通过预先给定取值范围内的一系列α值,计算得到对应ηn的理论值,点绘α-ηn曲线;其次,拟合该曲线得到α与ηn之间的高精度显函数表达式αn=f(ηn)作为替代函数。可将隧洞断面特性参数及水流条件代入式(9)求得ηn值,再将ηn代入其替代函数计算正常水深相应的充满度αn,就可以由hn=αnH计算正常水深hn。
在0≤α≤1.000范围内,以0.001为步长取1 000个计算点,代入式(8)采用MATLAB计算两个等号中间表达式值,即为与其对应正常水深模数ηn的理论值,并以α为纵坐标,ηn为横坐标,点绘其理论值关系曲线如图2所示。
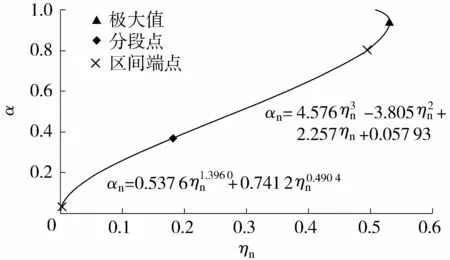
图2 标准型异形椭圆断面正常水深模数变化曲线
由图2和计算数据可知,当0≤α≤0.935时,标准型异形椭圆断面的正常水深模数ηn随充满度α的增大单调增大;当0≤α<0.368时,曲线斜率逐渐减小;当0.368≤α<0.935时,曲线斜率逐渐增大;当α=0.935时,正常水深模数达到极大值0.531 211。当α进一步增大,正常水深模数由极大值逐渐减小到满管流相应的理论值。
根据SL 279—2016《水工隧洞设计规范》的规定:在恒定流情况下,当通气条件良好时,洞内水面线以上空间不宜小于隧洞断面面积的15%。因此,满足规范要求的过水断面应符合以下条件:
A/A1≤0.85
(10)
将式(4)代入式(10)整理得到:
(11)
由于式(11)无法直接求解α值,故采用试算法。当A/A1=0.85时,试算得到α=0.766 711,即该值为符合规范要求的充满度上限。
对拟合区间适当外延,取α上限为0.800,根据工程经验取α下限为0.030,即充满度的拟合范围确定为0.030≤α≤0.800,对应的0.014 455≤A/A1≤0.880 370,一般能够满足无压隧洞的应用要求。如遇到在给定区间之外的情况,可根据式(8)采用MATLAB计算确定。
对0.030≤α≤0.800范围内的充满度α与正常水深模数ηn采用最小二乘法,通过MATLAB编程拟合。如果采用非分段函数的统一表达方式,会导致公式的形式非常复杂,涉及参数较多[13-14]。因此,根据图2正常水深模数曲线的变化特征,选择标准型异形椭圆断面最大宽度位置高度(zw=H/e)相应的充满度α=0.368作为拟合区间分段点。通过多次拟合与优化分析,提出分两段拟合的正常水深模数直接计算公式为
(12)
式中:条件①为0.030≤α<0.368,0.001 430≤ηn<0.178 512;条件②为0.368≤α≤0.800,0.178 512≤ηn≤0.494 646。
由实际明渠参数及水流条件求得正常水深模数ηn,判断其所在区间,选用相应区间内的充满度αn计算公式,求得正常水深对应的αn,则标准型异形椭圆断面的正常水深hn=αnH。
3 标准型异形椭圆断面的临界水深
3.1 明渠临界流基本方程
在明渠流量、断面形状和尺寸一定的情况下,急流与缓流这两种流态分界状态的断面单位能量最小,称为临界流,与此相应的临界水深是判别明渠流态的标准之一。因此,临界水深的计算是无压隧洞设计的又一重要参数。明渠临界流基本方程[12]为
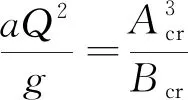
(13)
式中:a为动能修正系数,一般取1.0;g为重力加速度,取9.81 m/s2;Acr为临界水深对应的过水断面面积,m2;Bcr为临界水深对应的水面宽度,m。
由式(13)可知,临界水深仅与明渠流量、断面形状和尺寸有关,而与底坡i及糙率n无关。将式(3)和式(4)代入式(13)中,整理可得到关于标准型异形椭圆断面临界水深的隐函数表达式为
(14)
式中两个等号中间表达式为充满度或临界水深的隐含关系式。将式(14)右边的表达式设为标准型异形椭圆断面的临界水深模数ηcr:
(15)
由式(14)可知,临界水深模数ηcr与充满度α之间也存在隐函数关系ηcr=f(α)。可根据已知的隧洞断面特性参数及水流条件(断面参数H和流量Q等)由式(15)求得ηcr,而式(14)两个等号中间关于α的表达式包含对数、积分和指数运算,因此,仍然无法根据临界水深模数直接求得与其相应的充满度解析解。
3.2 临界水深的简化计算
临界水深的简化计算采用与正常水深相同的方法。在0≤α≤1.000范围内,以0.001为步长取1 000个计算点,代入式(14)采用MATLAB计算两个等号中间表达式值,即为与其对应临界水深模数ηcr的理论值,并以α为纵坐标,ηcr为横坐标,点绘其理论值关系曲线,见图3。
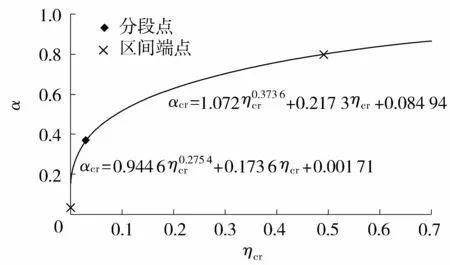
图3 标准型异形椭圆断面临界水深模数变化曲线
由图3和计算数据可知,当0≤α≤1.000时,标准型异形椭圆断面的临界水深模数ηcr随充满度α的增大单调增大;当0≤α<0.368时,曲线斜率较大,ηcr增长缓慢;当0.368≤α<0.980时,曲线斜率逐渐减小,ηcr的增长随之加快;当0.980≤α<1.000时,ηcr曲线以水平线为渐近线,ηcr迅速增长,当α=1.000满管流时ηcr的理论值趋向于无穷大。
标准型异形椭圆断面临界水深直接计算公式采用与正常水深直接计算公式相同的充满度分段拟合区间。通过MATLAB采用最小二乘法编程多次拟合与优化分析,提出分两段拟合的临界水深模数直接计算公式为
(16)
式中:条件①为0.030≤α<0.368, 0.000 003≤ηcr<0.030 254;条件②为0.368≤α≤0.800, 0.030 254≤ηcr≤0.492 807。
由实际明渠参数及水流条件求得临界水深模数ηcr,判断其所在区间,选用相应区间内的充满度αcr计算公式,求得临界水深对应的充满度αcr,则标准型异形椭圆断面的临界水深hcr=αcrH。
4 直接计算公式评价
正常水深和临界水深直接计算公式的精度评价采用相对误差分析法,相对误差δi计算公式为
(17)
式中:α为充满度给定值;αi为正常水深或临界水深对应的充满度简化计算值,在正常水深计算时,下标i=n,在临界水深计算时,下标i=cr。
由式(12)(16)计算的量纲一正常水深与临界水深的相对误差分布如图4所示。
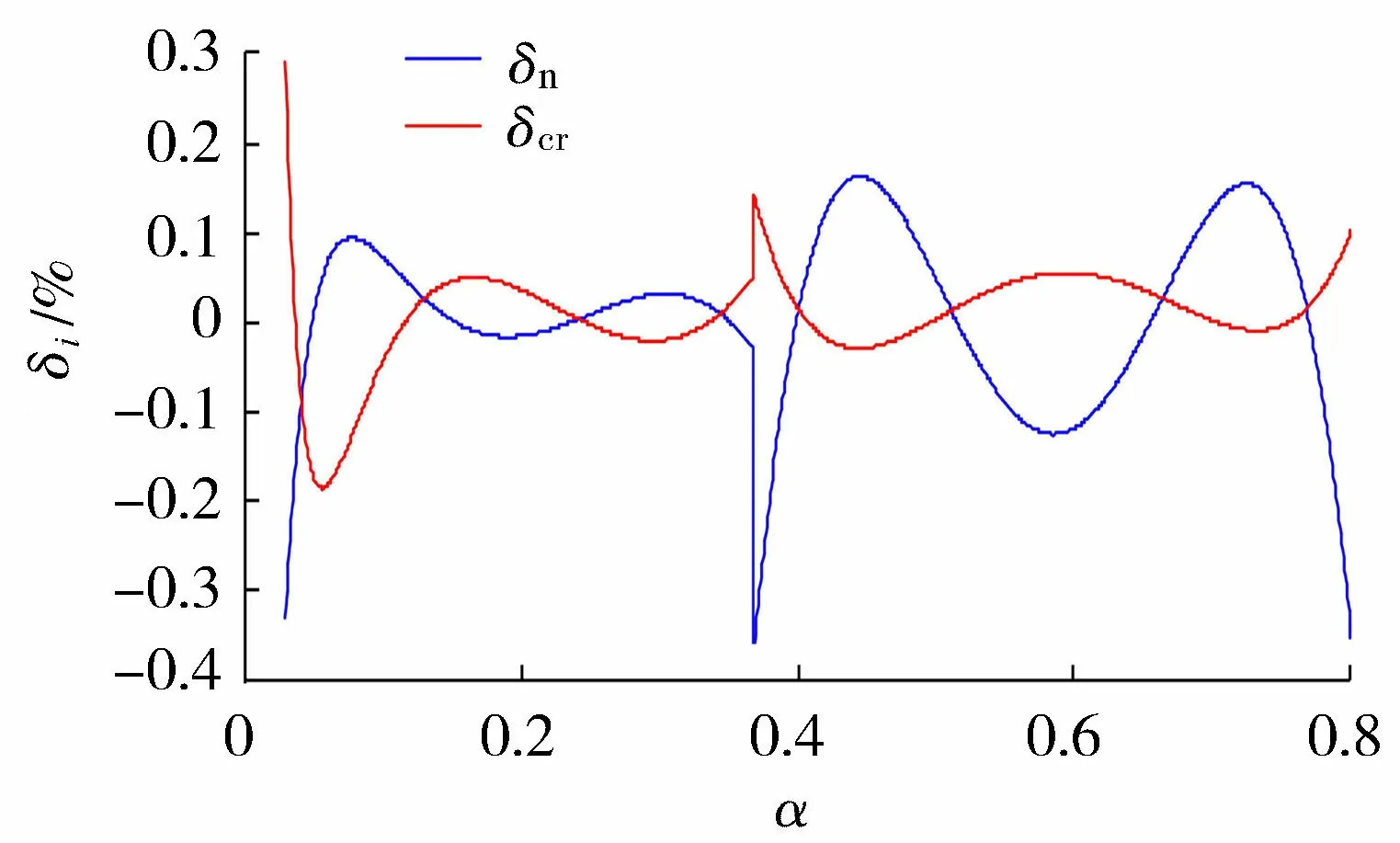
图4 正常水深和临界水深计算公式相对误差分布
由图4和计算数据可知,当0.030≤α<0.368时,正常水深直接计算公式的相对误差绝对值平均为0.034%,最大为0.329%;当0.368≤α≤0.800时,相对误差绝对值平均为0.103%,最大为0.362%,表明正常水深直接计算公式具有较高的精度。
由图4和计算数据可知,当0.030≤α<0.368时,临界水深直接计算公式的相对误差绝对值平均为0.045%,最大为0.288%;当0.368≤α≤0.800时,相对误差绝对值平均为0.030%,最大为0.139%,表明临界水深直接计算公式具有较高的精度。
5 算 例
某无压隧洞拟采用标准型异形椭圆断面,已知隧洞断面最大高度H=4.5 m,底坡i=0.004,糙率n=0.014,分别计算流量Q=15 m3/s和Q=48 m3/s时的正常水深hn和临界水深hcr。
5.1 正常水深计算
a. 当Q=15 m3/s时,由式(9)可得ηn=0.095 494<0.178 512,采用式(12)计算得αn=0.254 523,进而求得hn=1.145 354 m。经试算相应的正常水深理论值为1.145 234 m,相对误差为0.010%。
b. 当Q=48 m3/s时,由式(9)可得ηn=0.305 581>0.178 512,采用式(12)计算得αn=0.522 893,进而求得hn=2.353 019 m。经试算相应的正常水深理论值为2.353 613 m,相对误差为-0.025%。
5.2 临界水深计算
a. 当Q=15 m3/s时,由式(15)可得ηcr=0.012 429<0.030 254,采用式(16)计算得αcr=0.286 599,进而求得hcr=1.289 696 m。经试算相应的临界水深理论值为1.289 982 m,相对误差为-0.022%。
b. 当Q=48 m3/s时,由式(15)可得ηcr=0.127 277>0.030 254,采用式(16)计算得αcr=0.553 566,进而求得hcr=2.491 047 m。经试算相应的临界水深理论值为2.489 988 m,相对误差为0.043%。
在已知条件下,由临界水深均大于正常水深判断,该标准型异形椭圆断面无压隧洞在通过流量15 m3/s和48 m3/s时均发生急流状态的均匀流动。
6 结 论
a. 归纳了标准型异形椭圆断面的水力要素计算公式,推导了正常水深和临界水深方程,引入正常水深模数ηn和临界水深模数ηcr,给出了相应的隐函数方程。
b. 采用函数替代法,在充满度0.030≤α≤0.800范围内,以α=0.368为分界点,对α与ηn、α与ηcr分别进行拟合和优化分析,获得了分段直接计算公式。
c. 分析表明,标准型异形椭圆断面正常水深和临界水深直接计算公式相对误差的绝对值最大分别为0.362%和0.288%,均能达到较高的精度。
