经济政策不确定性、投资者情绪与股价同步性——基于TVP-VAR 模型的时变参数

任永平， 李 伟

(上海大学管理学院， 上海200444)

股价同步性是指在一段时期内证券市场上公司股票价格出现同时上涨或下跌的程度，即“同涨同跌”现象. 自Roll[1]提出用R2来反映单个股票与市场同涨同跌的关联性后， 股价同步性就成为股票市场的重要问题之一. 过高的股价同步性会降低资产定价效率[2]和经济运行效率[3-4]， 干扰证券市场筛选机制的运转[5-6]， 影响经济增长[7-8]， 从而带来消极的经济后果. 因此， 为避免股价同涨同跌带来的负面影响， 股价同步性的影响因素备受学术界的关注.

国内外学者对股价同步性影响因素的早期研究是从宏观的政策制度角度进行的.Morck等[9]发现产权保护机制完善的国家具有较低的股价同步性， 并推断“发达国家因其完善的法规制度使得股价中包含更多的公司特质信息， 所以股价同步性也会较低”. Fernandes等[10]分析了48 个国家的数据， 研究了内幕交易法和股价信息的关系， 认为内幕交易法的执行改善了价格信息， 降低了股价同步性. 游家兴等[11]发现随着制度建设的不断完善， 股价包含的公司特质信息越来越丰富， 股价同步性趋向减弱. Wang等[12]基于44 个国家的样本考察了会计准则对股票价格信息内容的影响， 发现会计准则质量较高的国家具有较低的股价同步性， 股价同步性和会计准则之间存在显著的负相关关系. Dong等[13]以美国证券交易委员会(U.S. Securities and Exchange Commission， SEC)要求上市公司必须使用可扩展商业报告语言(extensible business reporting language， XBRL)为研究背景， 探索信息成本如何影响公司特质信息的获取， 结果发现XBRL 报告可以促进财务数据标准化， 降低信息处理成本， 进而降低股价同步性. 与Wang等[12]相似， 史永等[14]研究了中国证券市场上XBRL财务报告对股价同步性的影响， 实证发现采用XBRL财务报告制度有利于抑制股价同步性的上升.

关于投资者情绪对股价同步性的影响， 国内外学者也展开了大量的研究. West[15]认为投资者心理偏差引发的非理性行为造成的股价同步性较低. Barberis等[16]利用行为金融学理论研究了投资者情绪对股价同步性的影响， 发现非理性投资者对公司的特殊偏好会引发非理性投资行为， 进而影响该公司的股价同步性. Greenwood等[17]也发现投资者情绪会影响股价同步性的高低. 很多学者还将投资者分为个人投资者和机构投资者分别进行研究. 在个人投资者情绪方面， Glaser等[18]研究发现， 个人投资者情绪和市场收益之间存在相互影响. 从短期来看， 市场收益对个人投资者情绪具有负面影响， 而个人投资者情绪对市场收益的正向影响则会滞后一个交易日. 余佩琨等[19]将散户投资者情绪和大户投资者情绪统归为个人投资者情绪，并研究了其与市场收益之间的关系， 认为借助市场收益可以预测个人投资者情绪指数， 反之则不成立. 而在机构投资者情绪对股价同步性的影响方面， 朱红军等[20]研究了证券分析师与股价同步性之间的关系， 发现证券分析师的信息搜寻活动能够明显降低股价同步性. 尹雷[21]研究发现机构投资者持股与股价同步性显著负相关， 并且机构投资者持股变化是影响股价同步性的决定性因素， 机构投资者持股比例和持股机构投资者数量是以机构投资者持股变化为中介发生作用， 这说明机构投资者基于信息的交易可以提高股价的信息含量， 从而降低股价同步性. 许年行等[22]研究认为机构投资者的“羊群行为”会提高公司的股价同步性， 而且机构投资者的“羊群行为”与股价同步性之间的正向关系更会因合格境外投资者(qualified foreign institutional investor， QFII)而增强.

综上所述， 对于政策制度和投资者情绪对股价同步性的影响， 已有研究获得了大量的理论和实证成果， 但在政策制度方面， 主要是从产权保护水平、法规制度、会计制度等方面进行研究， 没有涉及经济政策， 尤其是经济政策不确定性(economic policy uncertainty， EPU). 而中国股票市场的政策市现象比较明显， 那么经济政策的不确定性对中国股票市场的股价同步性会有怎样的影响呢？在投资者情绪领域， 国内研究主要是分别针对个人投资者情绪和机构投资者情绪对股价同步性的影响， 缺少宏观性的、考虑整个投资者群体的投资者情绪与股价同步性的关联. 此外， 国内外学者多采用回归模型及其衍生模型进行分析， 模型的核心是线性模型.但是随着时间的推移和环境改变， 回归模型及其衍生模型的变量之间的关系特征也处于不断变化的过程， 而回归模型却无法描述这种关系特征的动态变化.

因此， 为了准确描述经济政策不确定性和投资者情绪对股价同步性的时变性影响， 本工作采用时变参数向量自回归(time-varying parameter-vector auto regression， TVP-VAR)模型，借助TVP-VAR 模型的时变系数和冲击协方差矩阵捕捉各变量关系的非线性特征， 并通过模型的时变脉冲响应函数分析不同滞后期和不同时期内经济政策不确定性和投资者情绪对股价同步性的动态影响.

1 理论分析

1.1 经济政策不确定性与股价同步性

经济政策的不确定性对宏观经济发展和企业行为具有多方面的深刻影响. 2012 年， 国际货币基金组织在《世界经济展望》报告中明确指出了经济政策不确定性的负面影响， 认为经济政策不确定性会减少企业和家庭的投资、雇佣和消费， 进而抑制世界经济的复苏. 已有研究也认为经济政策不确定性会显著影响资本市场的股价反应， 甚至会对整个资本市场的股价波动产生影响. 经济政策不确定性上升会增加等待期权的价值， 企业投资下降， 银行信贷减少， 从而使得货币政策对企业信贷配置， 尤其是对短期信贷的调节能力下降， 即经济政策不确定性会显著降低货币政策有效性[23]. 货币政策有效性的下降又将会导致货币政策通过利率、货币供应量、公开市场业务影响股票市场的作用效果不明确， 增加市场“噪音”， 进而使得股价同步性上升.同时， 经济政策不确定性也会通过影响投资者理性行为对股价同步性产生影响: 一方面， 经济政策不确定性提升会增加投资者的风险感知和模糊性厌恶程度; 另一方面， 较高的经济政策不确定性也会影响投资者对政策信息的理解和掌握程度， 降低投资者的理性思维程度[24]， 由此造成投资者非理性投资行为增加， 使得股价同步性上升.

综上所述， 提出假设1: 当经济政策不确定性增加时， 股价同步性上升.

1.2 投资者情绪与股价同步性

传统金融理论认为， 人们的决策是建立在理性预期、风险回避、效用最大化， 以及相机抉择等假设基础之上的. 然而， 大量的实证研究表明， 传统金融理论的理性人假设与现实存在偏差， 人们的实际投资决策并非如此. 行为金融学发现， 投资者的认知具有局限性， 会表现出过度自信、损失规避、心理账户等非理性特征， 经常会作出非理性的投资行为. 这种非理性行为在经济系统中发挥着不容忽视的作用. 投资者需求假说认为， 投资者经常会自以为某市场事件传递了某种信息， 因此在偏好、情绪等非理性因素的影响下作出过度反应[16，25]. 当投资者情绪高涨时， 大量非理性投资行为就会促使股价同步性上升. 再从投资者认知心理学的角度看， 投资者的注意力是有限的， 投资者会更倾向于选择简单的分类决策规则， 而忽视公司层面信息，将有限的注意力集中在市场层面信息[26-27]. 因此， 投资者因注意力有限性而产生的简单分类决策行为倾向会导致公司特质信息无法有效融入股价， 从而推动股价波动与大盘同涨齐跌， 即股价同步性上升.

据此， 提出假设2: 投资者情绪对股价同步性具有正向影响.

2 研究设计

2.1 经济政策不确定性的度量

经济政策不确定性可以用EPU 综合指数衡量. 该指标由Baker等[28]构建并测算得出， 主要用于反映世界各大经济体的经济和政策的不确定性. EPU 综合指数主要由新闻指数、税法法条失效日指数和经济预测差值指数构成. 中国EPU 指数的计算则是利用了EPU 综合指数中的新闻指数， 以《南华早报》为分析对象， 对该报纸每月刊发的关于中国经济政策不确定性的文章进行识别， 将识别结果除以该报纸该月总刊发量得到该月的中国EPU 指数(http://www.policyuncertainty.com). 虽然中国EPU 指数只是新闻指数， 但Baker等[28]通过实证验证指出， 新闻指数与综合指数具有很强的相关性， 因此仍然具有代表性. 朱孟楠等[29]的研究也认为中国EPU 指数的测量精确度高达98.4%， 可以作为我国经济政策不确定性程度的衡量指标.

2.2 投资者情绪的度量

本工作的投资者情绪指标采用易志高等[30]构建的中国投资者情绪指标(Chinese investor composite sentiment index， CICSI). CICSI 融入了反映国内股票市场投资者情绪变化的主要变量， 包括封闭式基金折价(discount of closed end fund， DCEF)、成交量(turnover，TURN)、首次公开募股数量(initial public offering number， IPON)、上市首日收益(IPO returns，IPOR)、消费者信心指数(consumer confidence index，CCI)和新增投资者开户数(new investor accounts， NIA)等， 并运用主成分分析法确定各个变量的系数.

2.3 股价同步性的度量

根据已有研究[1，31]， 本工作通过以下模型对股价同步性进行估计，

式中: rit为第i 个公司第t 日的对数收益率; rmt为市场第t 日的对数收益率. 对模型(2)进行回归得到拟合系数R2. 根据统计学原理， R2反映了个股股价变动能被市场波动解释的部分，R2越大， 说明股价同步性越高. 由于本工作研究的是我国股票市场的整体股价同步性， 因此对我国A 股市场上市股票R2的日度数据取均值， 得到各月股票市场整体股价同步性.

图 1 显示了 2003 年 3 月至 2016 年 11 月的 EPU， CICSI 与 R2的走势情况， 图中将 R2扩大100 倍以消除与其他2 个变量的数量级差异. 可以发现， EPU 指数与R2出现高峰和低谷的时间比较接近， 表现出相似的趋势. CICSI 与R2则相反， 当R2处在高位时， CICSI 在低位或下跌; 当R2处在低位时， CICSI 会上涨或出现峰值. 由此， 从三者的走势可以确定， 经济政策不确定性、投资者情绪与股价同步性之间理应存在一定的关联性.

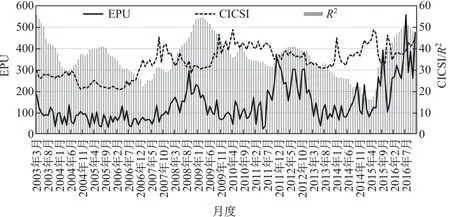
图 1 EPU， CICSI 与R2Fig.1 EPU， CICSI and R2

2.4 数据选取

考虑到数据的可得性， 本工作选取2003 年3 月至2016 年11 月的月数据， 共获得165 个月度数据. EPU 指数数据来自经济政策不确定性指数网站(http://www.policyuncertainty.com);CICSI 和R2均来自国泰安数据库. 由于国泰安数据库的R2是日度数据， 需要取均值以得到月度数据. 本工作对EPU， CICSI 和R2取对数增长率， 以对数增长率作为衡量3 个变量的变动指标.

3 TVP-VAR 模型构建

为了考察经济政策不确定性和投资者情绪对股价同步性的影响， 分别研究EPU 与R2以及CICSI 与R2的关联关系的时变性和非线性特征， 模拟特定时期经济政策不确定性和投资者情绪对股价同步性的影响， 本工作选取Nakajima[32]提出的带有随机波动的TVP-VAR 模型进行系统考察. 近年来， 国内对该方法也进行了广泛地运用， 但在股价同步性研究领域还未引入.本工作尝试借助该方法研究经济政策不确定性和投资者情绪对股价同步性的时变影响.

Sims[33]于1980 年首次提出向量自回归(vector auto regression，VAR)模型，随后众多学者在VAR 模型的基础上不断进行完善和演变. 2005 年， Primiceri[34]将时变参数引入VAR 模型中; Nakajima[32]则进一步完善了该模型， 提出了带随机波动的TVP-VAR 模型. TVP-VAR 模型描述如下.

首先， 引入一个标准的结构VAR 模型，

式中: t=s+1，s+2，···，n， t 表示时间， s 表示滞后期数; yt为由待考察变量组成的 k × 1 阶向量， k 为待考察变量的数量(待考察变量即为经济政策不确定性指数、投资者情绪指数及股价同步性);A 和B1，B2，···，Bs均为k×k 阶参数矩阵;μt衡量的是结构冲击，且μt～ N(0，ΨΨ)，其中

σ 为标准差. 假定同步结构冲击服从递归识别方式， 即矩阵A 为下三角矩阵形式，

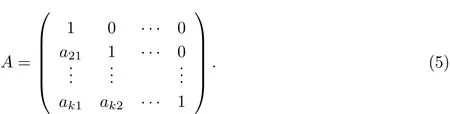
将式(3)重新简化为

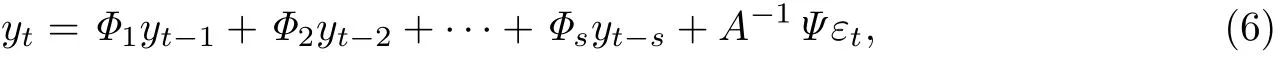
式中: εt为残差项， 且εt～ N(0，Ik)， Ik为单位矩阵; Φi= A-1Bi， i = 1，2，···，s. 将矩阵Φi的元素按行进行堆积处理并转换为β 形式， β 为k2s × 1 阶向量. 同时， 定义Xt=Ik⊗ (y′t-1，y′t-2，···，y′t-s)， ⊗ 为克罗内克积. 由此， 式 (6)可以表述为

此时， 式(7)中所有参数并不是时变的. 如果参数能随时间变化， 则是TVP-VAR 模型. 因此，带有随机波动性的TVP-VAR 模型可以表述为

式中: 参数βt， At及Ψt均具有时变性. 根据Primiceri[34]的研究， 可以对矩阵At中下三角的元素进行转换， 并表述为 a1= (a21，a31，a32，a41，···，ak，k-1)′， 且 ht= (h1t，h2t，···，hkt)′，hjt= Lnσ2jt， j = 1，2，···，k， t = s+1，s+2，···，n. 假设式(8)中的参数服从以下随机游走过程， 即 βt+1= βt+ μβt， σt+1= σt+ μσt和ht+1=ht+ μht， 且有

式中: βs+1～ N(μβ0，Ψβ0); αs+1～ N(μα0，Ψα0); hs+1～ N(μh0，Ψh0).

在实际分析时， 为了降低随机波动条件下似然函数的处理难度， 采用马尔科夫链蒙特卡罗(Markov chain Monte Carlo， MCMC)算法进行模拟抽样， 在获得模型待估参数分布的基础上对其进行估计.

4 实证检验与结果分析

4.1 参数设定及估计结果

表1 列出了TVP-VAR 模型的参数估计结果， 包括后验均值、后验标准差、95%置信区间、Geweke 概率和无效因子.

表1 参数估计结果Table 1 Parameter estimation results

从表1 可以看出， 参数的后验均值都在95%的置信区间内， Geweke 值都小于5%的临界值1.96， 表明不能拒绝参数收敛于后验分布的原假设. 无效因子表示要得到不相关样本所需要的抽样次数， 无效因子值越小越好. 从表1 中的无效因子值可以看出， (∑h)2的无效因子为121.64， 其余参数的无效因子均小于60， 远小于抽样次数10 000 次， 因此利用MCMC 算法得到的抽样样本对于TVP-VAR 模型的后验推断是足够的.

4.2 时变参数的特征分析

在参数不变的模型向量自回归模型中， 模型估计后参数只有一个估计值， 但是TVPVAR 模型中的每个参数的估计值都是随时间变化的.

图2(a)～(f)给出了样本的自相关系数， (g)～(l)表示样本路径， (m)～(r)为样本的后验分布. 从图(a)～(f)可以看出， 自相关系数均呈现出迅速下降的趋势， 最后都趋于0， 说明大部分样本不存在自相关性. 图(g)～(l)表明抽样数据都在样本均值附近稳定波动， 表现出明显的波动聚类现象， 且基本平稳， 说明利用MCMC 算法得到的不相关样本的数量是足够且有效的. 图(m)～(r)显示抽样样本分布明显收敛于后验分布， 因此抽样样本是收敛的. 由此， 根据图2 各时变参数的特征， 可以认为TVP-VAR 模型的结果是可靠的.

图2 时变参数的特征Fig.2 Characteristics of time-varying parameters

4.3 时变关系的特征分析

图3 和4 描述了经济政策不确定性、投资者情绪与股价同步性之间的动态时变关系.

图 3 EPU 与R2 的时变关系特征Fig.3 Time-varying relationship between EPU and R2

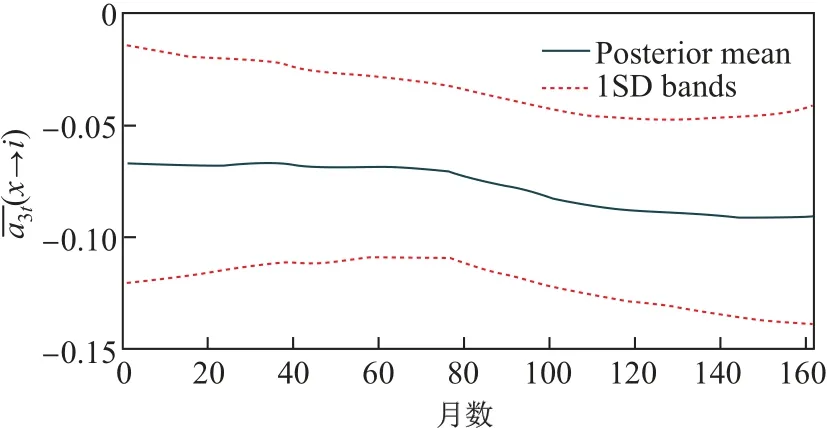
图 4 CICSI 与R2 的时变关系特征Fig.4 Time-varying relationship between CICSI and R2

图3 反映了经济政策不确定性对股价同步性的时变影响. 在大多数时间段， 经济政策不确定性对股价同步性的影响是正向的， 这一发现丰富了股价同步性在宏观领域的研究. 而在 2004 年 10 月至 2005 年 6 月以及 2012 年 2 月至 2013 年 12 月之间， 经济政策不确定性对股价同步性为负向影响， 这反映了该影响效应的作用方向会发生变动. 这种影响关系的非线性特征也正是利用回归分析方法无法捕捉到的动态特征.

图4 反映了投资者情绪对股价同步性的影响， 影响系数始终保持在-0.05 以下. 因此， 投资者情绪对股价同步性的影响主要是负向的， 且这种关系呈现为缓慢的增强态势. 所以， 利用TVP-VAR 模型不仅可以如已有研究一样对投资者情绪与股价同步性的关系进行定性分析，同时还可以对其影响强度进行动态量化.

4.4 不同时滞期的脉冲响应分析

对于TVP-VAR 模型， 可以设置不同的滞后期数来反映单位冲击变量对被冲击变量在不同滞后期形成的影响. 图5 和6 分别给出了在不同滞后期下股价同步性对经济政策不确定性(εp→ i)和投资者情绪(εx→ i)的脉冲响应函数. 参考金春雨等[35]的研究， 本工作选取冲击影响时间约束为0(短期)， 2(中期)和6(长期)个月. 从图5 和6 可以看出， 样本期间经济政策不确定性对股价同步性的影响具有时变效应， 不同时间约束下的影响程度不同; 投资者情绪对股价同步性的影响比较平稳.

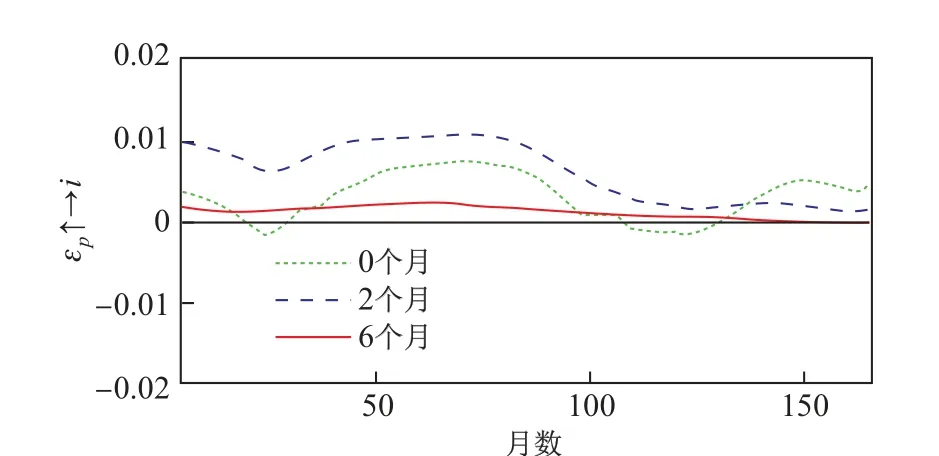
图5 R2 对EPU 的等时间间隔脉冲响应函数Fig.5 Equivalent time interval impulse response function to EPU for R2

图6 R2 对CICSI 的等时间间隔脉冲响应函数Fig.6 Equivalent time interval impulse response function to CICSI for R2

4.4.1 经济政策不确定性对股价同步性的脉冲响应函数及影响机理

从图5 的等时间间隔脉冲响应函数可以看出， 经济政策不确定性对股价同步性的影响主要是正向的， 影响强度随时间变化， 基本验证了经济政策不确定性增加会导致股价同步性上升的假设. 具体就短期(0 个月)和中期(2 个月)而言， 经济政策不确定性对股价同步性的时变影响走势比较相似， 股价同步性对经济政策不确定性冲击的中期响应始终在0 以上， 短期响应也是大部分时间段为正向影响. 而就长期(6 个月)而言， 经济政策不确定性对股价同步性的影响比较平稳， 140 期(即2014 年10 月)以前， 股价同步性对经济政策不确定性冲击的响应程度大于 0， 但比较微弱; 2014 年 10 月之后则为 0.

经济政策不确定性对股价同步性的影响主要是从货币政策有效性和投资者理性行为两个方面产生作用. 图5 的脉冲响应函数显示， 短期和中期的经济政策不确定性越大， 股价同步性越高. 一方面， 较高的经济政策不确定性会因对信贷调整能力的下降而明显降低货币政策的有效性， 使得货币政策对市场的作用效果不明确， 这无疑会增加市场上的“噪音”， 影响私有信息融入股价， 继而推动市场股价同步性上升. 另一方面， 经济政策不确定性的增加会提升投资者的风险感知和模糊性厌恶水平[36]， 降低投资者对政策信息的理解程度， 使投资者在非理性思维的基础上作出投资决策. 在大量非理性投资行为的作用下， 各公司股票价格极易表现出与大盘同涨同跌的互动特征， 即市场股价同步性较高. 但由于地方政府对银行长期信贷的干预， 货币政策对长期信贷的调节作用不会受到高经济政策不确定性的显著影响[23]. 因此， 正如图5 所显示的， 长期的经济政策不确定性对股价同步性的影响较小.

4.4.2 投资者情绪对股价同步性的脉冲响应函数及影响机理

从图6 的等时间间隔脉冲响应函数可以看出， 股价同步性对投资者情绪冲击的短期、中期和长期脉冲响应曲线均始终为负， 其中投资者情绪对股价同步性的短期影响最为强烈， 长期影响最为微弱; 并且， 投资者情绪对股价同步性的短期影响明显呈现出逐年增强的趋势.

股价同步性对投资者情绪冲击的脉冲响应曲线为负， 表明投资者情绪的提升会促使股价同步性的下降， 与投资者情绪对股价同步性具有正向影响的假设相反， 也与Peng等[26]、Kumar等[37]、李昊洋等[38]得出的投资者情绪高涨会提升股价同步性的结论相反. 这可能是由于投资者因自身个体差异， 在情绪作用以及不同的投资环境和投资目标下对同一只股票的期望价格和收益也会存在差异. 因此， 在复杂多变的情绪作用下， 投资者会作出多样化的投资决策; 投资者情绪越高， 投资者的期望差异也会越大、越明显， 表现在股票市场上即为股价同步性的下降. 并且， 若投资者情绪高涨， 投资者的关注度也会随之提升， 投资者分析增加， 易使得更多的公司特质信息进入市场， 从而降低股价同步性[39]. 正是由于我国金融市场的持续发展，IPO 数量和投资者群体每年都在增长， 支撑了投资决策多样化的趋势， 使得期望差异扩大; 以及随着投资者理性投资决策水平的不断提升， 更多公司特质信息融入股价， 使得投资者情绪对股价同步性的负向影响逐渐增强.

4.5 不同时间点的脉冲响应分析

本工作以3 个EPU 指数高点的发生时间(除2016 年7 月样本尾端指数)作为对比时间点.(1) 2008 年9 月(t=67). 2008 年， 美国次贷危机对我国经济的影响开始显现， 政府出台了若干应对措施， 但刺激性政策又转化为国内通胀压力， 政策进一步刺激的空间有限. 在该时期， 我国面临政策选择的双重困难. 基于此， 本工作选取了该时期经济政策不确定性指数最高的时点， 即 2008 年 9 月. (2) 2011 年 11 月 (t = 105). 2011—2012 年， 由于面临政府换届， 国内经济政策不确定性增大， 且欧债危机已达到高潮， 外部环境对我国经济发展影响的不确定性也急剧增大. 因此， 本工作选取了该时期经济政策不确定性指数最高的时点， 即2011 年11 月. (3)2015 年 9 月 (t=151). 2015 年， 我国 GDP 增速落到了 25 年以来的最低值， 政府下一步的经济政策走向得到了全球关注， 2015 年的“夏季股灾”更是加剧了对经济政策不确定的担忧. 因此，本工作选取了该时期经济政策不确定性指数最高的时点， 即2015 年9 月.

图7 给出了不同时间点股价同步性对经济政策不确定性冲击的脉冲响应. 可以看出， 3 个时间点的经济政策不确定性对股价同步性存在正向影响， 并且股价同步性对经济政策不确定性冲击的响应形态基本是一致的， 均是在当期产生一个正向反应， 并在增强至峰值之后逐渐减弱， 说明经济政策不确定性对股价同步性的作用不存在时滞， 都是在初期即产生影响. 2008 年 9 月在第 2 期达到峰值后逐渐下降， 在第 4 期趋近于 0; 2011 年 11 月在第 1 期达到了峰值， 在第4 期趋近于0; 2015 年9 月同样是在第1 期就达到了峰值， 随后在第3 期趋近于0.可以看出， 在第0 期， 2008 年9 月经济政策不确定性冲击对股价同步性的作用效果最显著，2011 年 1 月最小; 2008 年 9 月和 2011 年 11 月都是在第 4 期趋近于 0， 2015 年 9 月则是在第 3 期趋近于0. 因此， 从经济政策不确定性对股价同步性的影响程度来说， 次贷危机时期的影响程度最深; 从影响时间来看， 次贷危机时期和欧债危机时期的影响时间最长. 由此可见， 经济政策不确定性会促使股价同步性上升， 但在不同时间点上的影响程度和影响时间存在差异.

图8 给出了不同时间点股价同步性对投资者情绪冲击的脉冲响应. 3 个时间点的股价同步性对投资者情绪冲击的反应形态基本是一致的， 都是在当期产生一个负向反应， 随后反应程度逐渐减弱， 并在第10 期之后趋近于0. 但不同的是， 次贷危机时期的负向反应最大值出现在第1 期， 欧债危机时期以及“夏季股灾”时期的负向反应最大值出现在当期. 可以看出， 次贷危机时期投资者情绪对股价同步性的影响程度最深; 而在影响时间上， 3 个时期的影响时间是基本一致的. 由此可见， 投资者情绪的提高可促使股价同步性降低， 但在不同时间点上的影响程度存在细节差异.

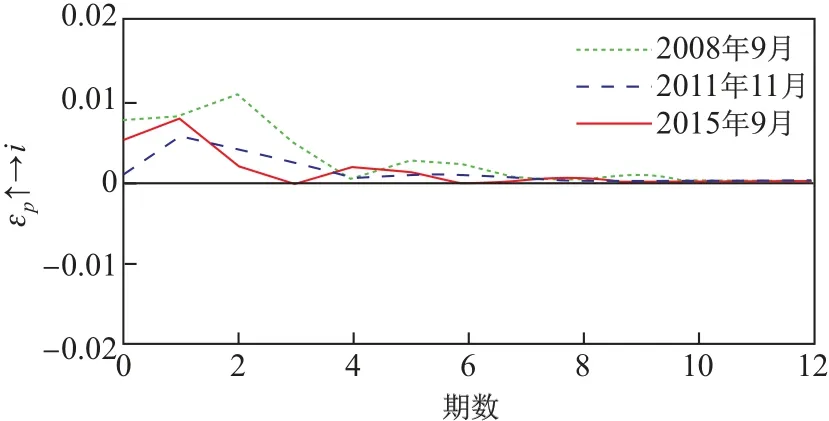
图 7 R2 对EPU 的时变脉冲响应Fig.8 Time-varying impulse response to EPU for R2

图 8 R2 对CICSI 的时变脉冲响应Fig.8 Time-varying impulse response to CICSI for R2

5 结 论

随着我国经济的不断发展， 经济政策、金融政策和金融市场结构等也随之不断变化， 传统的线性回归方法已无法准确描述经济政策不确定性、投资者情绪与股价同步性之间的动态关系. 本工作以2003 年3 月至2016 年11 月的经济政策不确定性、投资者情绪和股价同步性的月度数据为样本， 运用带有随机波动的TVP-VAR 模型对经济政策不确定性和投资者情绪对股价同步性的影响效应进行实证分析， 得到了以下主要结论.

(1) 经济政策不确定性对股价同步性的影响具有较强的时变特性， 在不同的滞后期数具有不同的表现， 短期和中期的经济政策不确定性对股价同步性主要为正向影响， 时变性较强; 长期影响虽仍为正向影响， 但影响程度微弱.

(2) 投资者情绪可以抑制股价同步性， 在不同滞后期数均表现为负向影响， 其中短期影响最为明显， 长期影响则较弱. 随着我国金融市场的持续发展和IPO 数量、投资者群体的增长以及投资者理性投资能力的提升， 投资者情绪对股价同步性的影响逐渐增强.

(3) 在不同时间点下， 经济政策不确定性和投资者情绪对股价同步性的影响在影响程度和影响时间上存在差异. 从影响程度来看， 次贷危机时期的经济政策不确定性和投资者情绪对股价同步性的影响程度最深; 从影响时间来看， 次贷危机和欧债危机时期的经济政策不确定性对股价同步性的影响时间最长， 投资者情绪对股价同步性的影响则没有明显的时间差异.

通过本工作的研究结论， 可以得到如下启示: ①经济政策不确定性对股价同步性具有较大影响， 为保证金融市场的健康发展， 要不断完善政策调控体系， 对经济政策不确定性的负面影响进行及时控制; ②鉴于投资者情绪对股价同步性的影响逐渐增强， 证券监管部门应积极地规范和引导投资者行为， 提高投资者信息交易能力， 避免情绪化行为， 促进市场理性化; ③要充分考虑经济政策不确定性和投资者情绪对股价同步性影响的动态变化， 选择合理有效的调控手段， 制定出台相应的调控政策， 提高调控效率.