能量法在基坑支护结构纵向变形分析中的应用
2020-12-09刘习生申洋
刘习生,申洋
(1.中铁上海工程局集团华海工程有限公司,上海201101;2.中铁第四勘察设计院集团有限公司,武汉430063)
1 引言
深基坑形状不规则的基坑时,采用三维分析方法进行分析才比较准确[1]。关于空间效应的计算,一些学者用平面应变比(PSR)评估空间效应大小,或通过现场实测数据、数值模拟,认为影响空间效应大小的主因是开挖的长深比、软弱土层的位置、支撑抗压刚度。Roboski和Finno[2]则提供了从二维平面状态下土体位移计算值预测三维平面状态下位移的公式。而针对黏性土的MSD(Mobilized Strength Design)理论最早由剑桥大学的Bolton提出。本文在纵向地下连续墙变形中引入MSD原理,对三维空间下基坑的纵向变形进行预测,提出软黏土中基坑空间效应系数的计算方法。
2 基于能量法的MSD预测
对于设有内支撑或外部锚杆的深基坑,开挖某道支撑以下若干土体时,围护结构的水平位移增量Δw,理论上假定为余弦函数。Δw可用式(1)表达:

式中,Δw为该道支撑下方墙体水平位移增量,m;Δwmax为最大水平位移增量,m;l为变形影响深度,m;y为计算点距离原点的竖向深度,m。
定义平均剪应变增量为发挥的剪应变增量Δγmob,则:

式中,Ω为计算积分区域;Δγ为剪应变增量。各分区域土体的应变能U用式(3)表示:
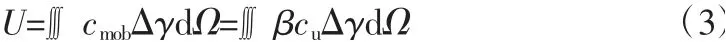
式中,β为不排水抗剪强度发挥系数;cmob为不排水抗剪强度发挥值;cu为不排水抗剪强度。
土体受到的外力功W外用式(4)表示:

式中,γt为土体重度;ν为土体竖向位移,m。总能量平衡表达式为:

式中,Wi为各区域土体受到的外力功;Ui为各区域土体的应变能,i=1,2,3,4,分别代表如图1所示的4个区域:ABCD,CDE,EFH和FHI。
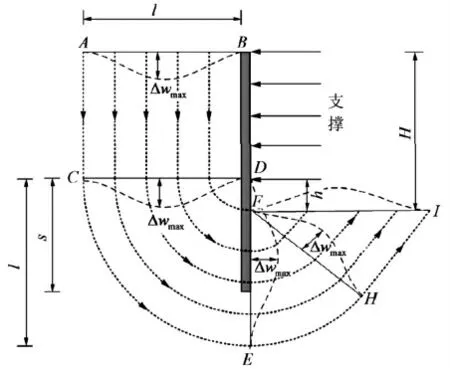
图1基坑开挖变形机制示意图

MSD法根据直剪试验结果来确定β与剪应变的关系。正常固结黏性土β-剪应变曲线的关系见式(7):

首先根据β确定不排水抗剪强度发挥值cmob,然后依据黏土体的能量守恒,计算围护结构的最大水平位移。
3 基坑围护结构地连墙纵向变形规律
支撑作用下板的弹性理论挠度表达式为:

式中,a、b为计算板的尺寸;A为待定常数,x,y为计算点的坐标。将墙体内力功用位移表示,得到式(9):

式中,E为材料的弹性模量;I为惯性矩;ν1为弹性泊松比。
假定地下连续墙弯曲应变能,储存在底层支撑与地连墙墙底长度范围的围护结构中,有:

式中,S为底层支撑到地下连续墙底的长度。积分后得到墙体横截面弯曲应变能为:

考虑墙体纵向变形的弯曲应变能,将纵向墙体划分为长度差为Δx的多段,各段之间由于变形差异产生的应变能为:

式中,x为纵向长度。参考二维平面内地连墙变形计算公式,考虑空间效应,假定地下连续墙位于最下层支撑以下部分纵向变形曲线为:
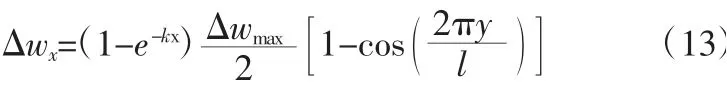
式中,k为空间效应下作用长度相关系数;e为孔隙比。
将纵向地下连续墙变形曲线分为若干段,每段长度Δx,假定各分段内均服从能量守恒,取Δx=1m。
4 引入纵向变形曲线的MSD三维计算方法
考虑基坑端部横墙的约束作用及双向墙体应变能P及Px,能量守恒公式可以调整为:
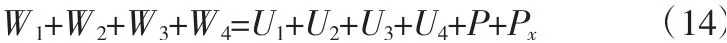
墙体纵向弯曲应变能为:

式中,k与地连墙空间效应作用的长度相关,取0.5;x为地下连续墙纵向计算位置。
鉴于土体发生塑性变形其强度未达峰值,定义不排水抗剪强度的发挥值cmob:

引入基坑施工空间效应系数Km,定义为三维空间条件下(cmob3D)与平面二维状态下的比值,即:

5 算例
无锡某地铁站基坑,基坑围护地下连续墙深度27m,第1道是混凝土支撑,水平间距为8m,第2道和3道钢支撑水平间距为4m。土体参数如表1所示,基坑结构平面、剖面如图2所示。
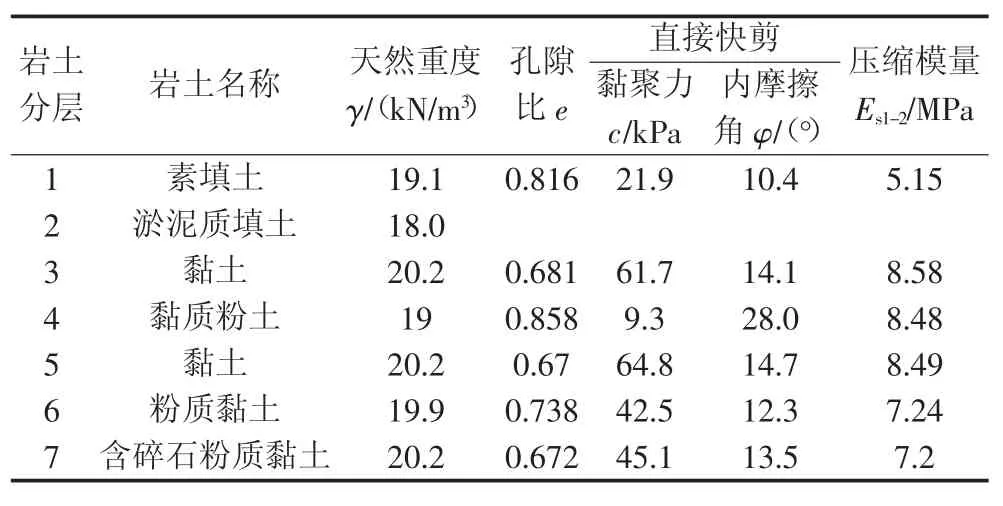
表1土体工程物理参数

图2基坑支护结构示意图
5.1 不排水强度
基于CPT结果的不排水抗剪强度公式计算公式:

式中,qc为锥头阻力;标贯Nk取16;σv0为土的重度。根据本工程的CPT典型分布数据,取qc=0.08+0.081d,如图3所示,cu与深度d的关系曲线为:

不排水抗剪强度随深度变化关系式为cu=5+3.8d性变化。该黏土的不排水剪应力-剪应变曲线拟合后为:


图3 CPT检测曲线
5.2 计算结果分析
计算地下连续墙的水平位移,结果如图4所示。
距离基坑角部距离越近,水平位移绝对值越小,变形曲线在开挖深度8m后趋于稳定。
基坑纵向各点不排水强度调动率反映纵向各计算点设计时对土体自身强度的利用程度,反映了设计的经济程度。由于交点位置地下连续墙的“全断面约束”,相对于基坑中点,角部区域安全性高。黏土空间效应系数计算值如图5所示。

图4地下连续墙明挖段水平位移

图5黏土基坑的空间效应系数分布
空间效应系数实际上反映了基坑对于周边士体自身强度的利用程度。基坑拐角位置,土体自身强度利用率明显低。
6 结论
本文基于MSD方法,考虑了地下连续墙纵向变形特征,引入纵向弯曲应变能修正现有MSD方法中。得到以下结论:
1)现有空间效应基于无黏性土的三维失稳模型的假设不完全适用于软黏土基坑。在软黏土中采用的空间效应公式应满足局部剪应变假定。
2)相同地质条件及支护设计参数下,靠近基坑拐角的全约束位置,其土体自身强度利用率低。
