基于CFD的超声波流体测量影响因素的模拟

孙发君， 林惠阳， 刘自帅， 罗玉龙， 郝 军

(京源中科科技股份有限公司， 北京 102488)

随着我国经济的快速发展，工业领域也在不断发展，流量计在工业生产过程中具有重要的作用[1]。其中，超声波流量计以其量程比宽、无压损、计量精度高、易安装维护等优点[2]，逐渐取代了传统易磨损、精度低以及稳定性差的机械式流量计。超声波流量计的广泛应用，对节能减排起到了重要作用。

鉴于市场的迫切需求，目前国内外流量计研究方向主要集中于3个方面：流场适应性分析、信号检测优化以及采集信号处理技术。其中，管道流场的优化设计是提升流量计测量精度的一种有效方法。尽管目前国际上已有文献对此进行了初步的理论和实验研究[3-4]，但还缺乏系统和定量的分析，一些分析结果难以推广和应用。国内外相关学者[5-9]对超声波流量计(热量表)内的流场特性进行了数值研究，分析了不同因素的影响，优化了某一特定超声波流量计(热量表)的设计。

针对上述背景，本文基于计算流体力学原理，采用CFD软件，对某DN50的超声波流量计的多种工作状态进行了三维数值仿真，通过仿真得到了超声波流量计内流场分布规律，并全面分析了关键截面、关键线上的速度分布规律，并进一步计算得出K系数，并通过实验检测平台验证模拟的准确性，后续研究可采用模拟研究的方法。通过改变边界条件和影响因素，分析不同因素对超声波流量计内流体流动的影响，借助仿真得到的一些规律对于该产品的后续设计具有一定的指导作用。

1 超声波流量计原理

超声波流量计是通过检测流体流动对超声脉冲的影响来测量流量的仪表。包含2个传感器：超声信号发射器和接收器，当流体静止时，顺流与逆流方向的超声脉冲传播时间相等；当液体流动时，顺流方向的信号传播时间短于逆流方向，顺逆流的时间差与流体的流速相关，由此可以计算出超声脉冲传播路径上流体的线平均流速。超声波流量计测量基本原理如图1所示。

图1 超声波流量计测量基本原理图

(1)

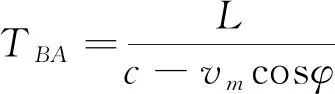
(2)

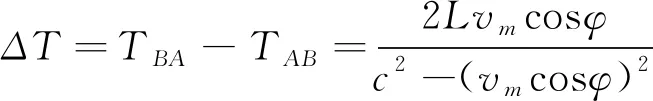
(3)

式中：TAB为超声脉冲从A发射到B接收(顺流)的时间，s；TBA为超声脉冲从B发射到A接收(逆流)的时间，s；vm为传播路径上的流体的线平均速度，m/s;c为超声脉冲速度，m/s；L为声道之间的距离，m；φ为水流方向与超声波脉冲方向夹角(锐角)，rad。

超声脉冲在水中的声速远远大于水流速度vm≪c，因此vmcosφ可以忽略，故：

(4)

可见，流体流速和超声脉冲顺逆流的时间差成正比，故：

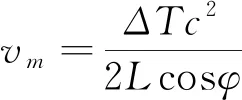
(5)

管道流量：

(6)

式中：vD为管道截面平均速度，m/s；D为管道内径直径，m；Q为管道流量，m3/s。

超声波流量计测量通常采用的是超声波传播路径上流体的线平均流速，而实际管道横截面上的流速分布是呈抛物线形态的，这就造成了断面流速计算造成的误差[10]，如下图2和图3所示，可见传播路径上的流体的线平均速度不等于管道截面平均速度，因此，要计算管道实际通过流量，需要对传播路径上的流体的线平均速度进行修正，引入修正系数K，关系如下式：

(7)

根据式(5)-(7)，计算得到管道的流量为：

(8)

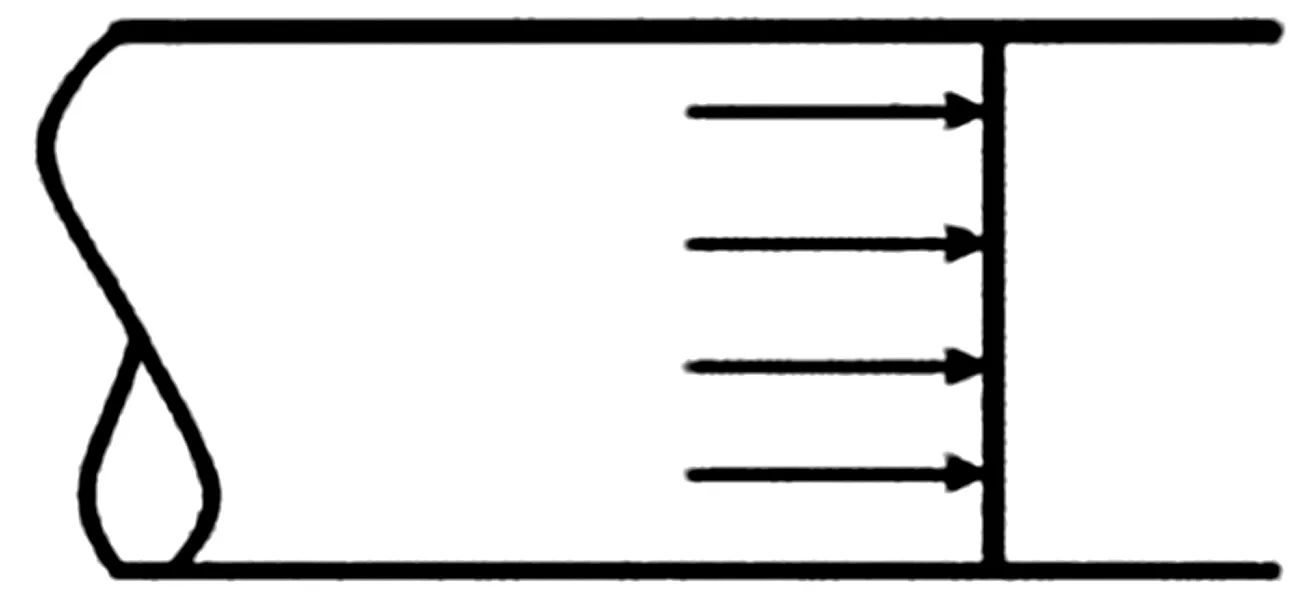
图2 理想流速分布

图3 实际流速分布

超声波流量计是一种非接触式仪表，流体中未设置任何阻碍件，属无阻碍流量计，对流束无影响，它既可用于任何流体，特别是具有高黏度、强腐蚀，非导电性等性能的液体的流量测量，也能测量气体流量，因此应用越来越广泛。

2 实验台简介及实验数据

2.1 实验台简介

该流量检定实验台包括加热储水箱、变频恒压水泵、稳压罐、超声波流量计安装台及高精度质量标准称等设备，通过上位机控制该实验台。

选取某一特定水温，通过调节管道阀门获取某一相对稳定的流量点，通过测量一段时间内流过该管段的流体质量，并结合当前水温，可得出流过管道的流体体积，进而可换算出流过该管道的平均面速度，超声波流量计可测得平均线速度，可计算出当前水温下当前流量点所对应的K值，流量检定实验台如图4所示，原理示意如图5所示。

图4 流量检定实验台实物图

图5 流量检定实验台的原理示意图

2.2 实验结果

由表1发现，流量越小，修正系数K越大，随着流量的增大，修正系数K先快速减小，再缓慢减小并接近1，意味当流量越大时，流场分布比较均匀并稳定，修正系数K随流量的变化如图6所示。

表1 流量检定实验数据

图6 修正系数K随管道流量的变化图

3 模拟仿真及验证

3.1 CFD简介

CFD是计算流体力学英文的简称，是通过计算机进行数值模拟，分析流体流动和传热等物理现象的技术[11]。是流体力学和计算机科学相互融合的一门新兴交叉学科，从计算方法出发，利用计算机快速的计算能力得到流体控制方程的近似解。

一般说来，采用CFD解决某一实际问题分为三个过程：前处理、求解及后处理。前处理包含计算域的搭建、网格的划分及边界条件的设定，其中网格的划分通常要占到CFD分析时间的40%以上，并且直接关系到求解精度。求解过程是基于前处理的基础上，检查网格质量和确认计算单位，然后设置求解器，再选择计算模型和流体物性等边界条件，然后开始进行迭代计算。后处理是在已经收敛的计算结果中继续处理，得到直观清晰的数据或图表。

3.2 流体域提取及网格划分

为了开展计算流体力学(CFD)仿真，需要对研究对象工质流动的区域建模，然后进行网格划分。本文根据DN50的超声波流量计的金属固壁区域的三维设计图(如图7所示)，通过补截面、布尔运算等处理，抽取到了产品的流体域，如图8中所示。

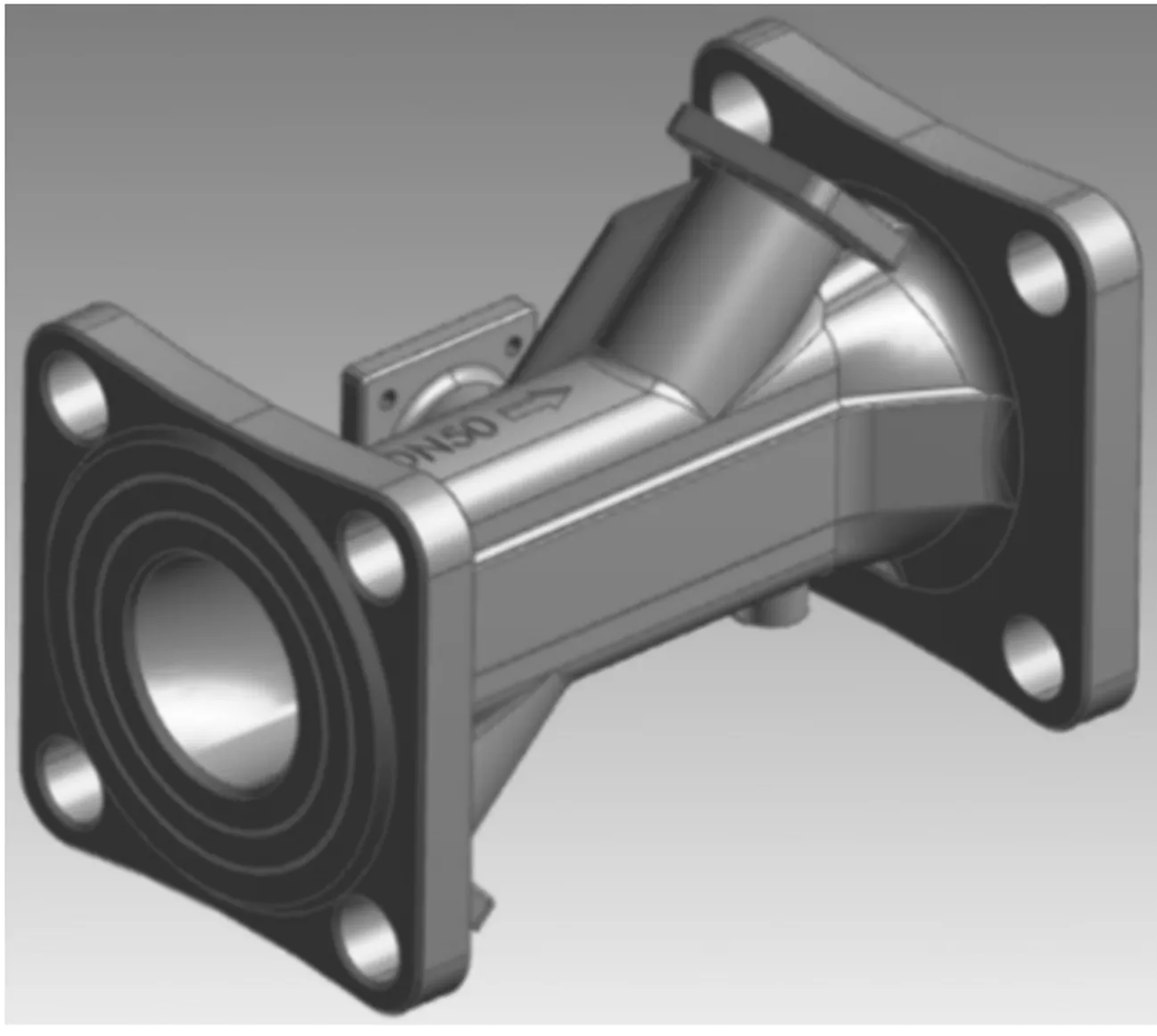
图7 超声波流量计三维设计图

图8 计算域几何模型示意图

通过分析认为，工质在接近或者进入到超声波流量计时，已经是充分发展的流动状态，但是图8中计算域的出入口就是实际超声波流量计产品的出入口，流体的入口效应和出口效应(尤其是入口效应)无法考虑，这将对仿真的结果造成影响。因此，在图8所示的流体域基础上，分别在入口前增加10 D管段，在出口后增加5 D管段。网格均采用六面体结构化网格来保证结果的收敛性，并且对流体域的靠近壁面的区域的网格进行了加密，最小网格厚度在0.05 mm左右，保证了在速度梯度较大的边界层中，计算结果仍然具有较高分的分辨率，如图9所示。

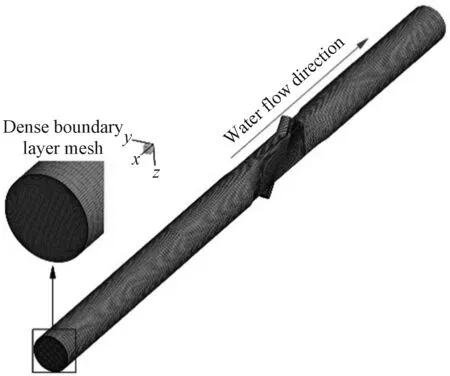
图9 流体域的网格划分示意图

3.3 边界条件设置

结合超声波流量计DN50产品的说明手册，有3种典型流量工况，分别为：常用流量15 m3/h，分界流量0.6 m3/h，最小流量0.15 m3/h。因此，选取管道流量为常用流量、分界流量、最小流量三种流量；流体温度设置为50 ℃时；出口为给定的压力出口，出口压强设置为0.5 MPa；除入口和出口之外，其余壁面均设置为固定无滑移的绝热壁面，壁面粗糙度根据工程实际设置为8 μm，如表2所示。

其中，由于分界流量是工程领域认为的层流和湍流之间转变的拐点，因此，为了保证仿真结果的科学性，在分界流量(0.6 m3/h)条件下，分别采用层流和湍流模型模拟计算。

表2 边界条件设置

3.4 层流及湍流模型

雷诺数是流体力学领域中一个非常重要的物理量，其表达式如下所示：

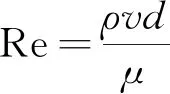
(9)

式中：ρ为密度，kg/m3；v为速度，m/s；d为圆管直径，m；μ为流体的黏度，Pa·s；Re为雷诺数。

雷诺数Re的物理意义是惯性力与黏性力的比值。雷诺数较高意味着：流体当前的运动状态中惯性力占主导地位；而雷诺数较低则代表流体在当前的状态下，黏性力占主导地位。

工程领域按照流体流动时雷诺数的大小，将流动状态分为两种：层流和湍流。两种流动状态截然不同，层流的流动相对规则，各个部分分层流动，层与层之间互不掺混，流体质点的轨迹线是光滑而稳定的。湍流的特征则截然相反，流体运动极不规则，各个部分之间激烈掺混，流体质点的轨迹杂乱无章，而且流动不稳定。

本文研究DN50的超声波流量计，在最小流量(0.15 m3/h)下，流动状态为层流；常用流量(15 m3/h)下的流动状态为湍流；而在分界流量(0.6 m3/h)下，流动状态可能是层流，也可能是湍流。对应两种不同的流动状态，有不同的控制方程来描述这两种流动。

针对层流流动，可以直接用数值方法求解粘性流动的连续性方程和动量方程来实现，连续性方程和动量方程如下式所示：

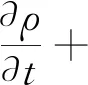
(10)

(11)

在很多流动场合，层流流动已经有了解析解，并且与实验数据吻合良好。而对于湍流流动，学术界虽然已经提出多种湍流模型，然而没有哪一种湍流模型能够适用于所有的流动现象，湍流模型的选取不仅需要依据具体的物理问题而定，还要综合考虑计算精度、计算成本等问题。经过前期的尝试和初步计算，综合权衡仿真所需时间和仿真精度，本文选用标准的k-ε两方程湍流模型。三维直角坐标系下该模型的控制方程包括湍动能(k)方程和湍动能耗散率(ε)方程：

(12)

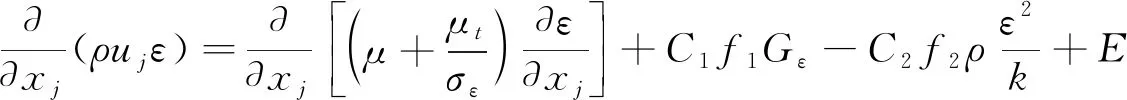
(13)

其中湍动能生成项和湍流粘性系数分别为：

Gk=

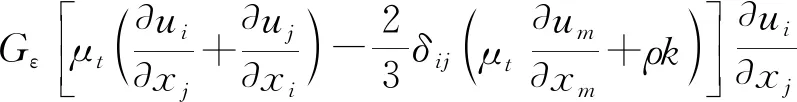
(14)

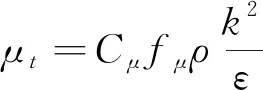
(15)

3.5 模拟结果

借助CFD软件，基于上述边界条件模拟得到不同流量下的脉冲路径线平均速度、管道截面平均速度，进而求得修正系数K，如下表3所示。由表3发现，流量越小，修正系数K越大，随着流量的增大，修正系数K越来越接近于1，与实验测得的规律一致。其中，当流量为0.6 m3/h时，采用了层流和湍流2种模型，从计算结果的比较可以发现，层流模型得到的K系数更接近实测，因此后续0.6 m3/h的模拟计算应该采用层流模型。

把模拟值和实测值对比得到表4，从表4可以看出，线速度和面速度的模拟值比实测值要略大一点，系数K的模拟值比实测值略小一点。模拟和实测得到的变化趋势一致，且系数K的相对误差在1%以内，因此可以用模拟的方法，来研究实验无法完成的超声波技术的优化研究，或代替部分实验，节约时间和成本。

表3 模拟结果

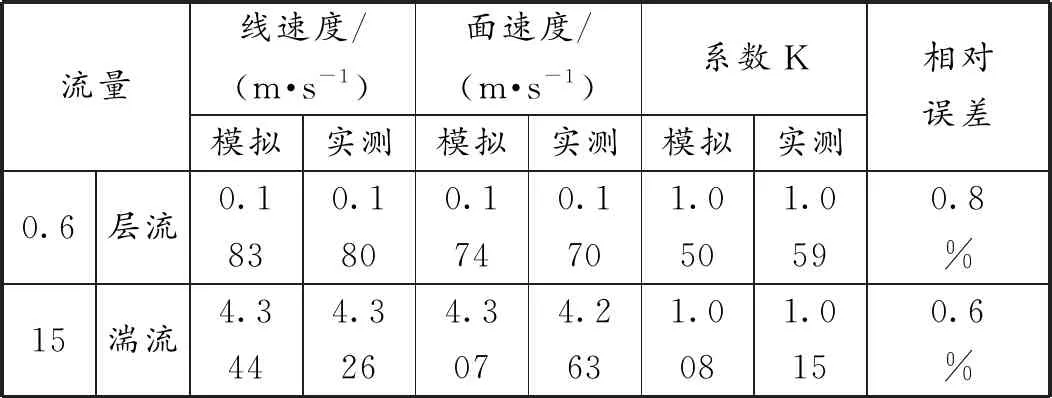
表4 实验与模拟结果对比

4 优化分析

借助CFD模拟方法，可表计的结构、设计进行优化，也可对安装位置、温度等因素的影响进行分析。模拟研究比理论研究功能更为强大，比实测研究更为节约成本和精力，因此本文提出采用模拟研究的方法。可优化超声波流量计的结构设计，如表计的哪种变径方式(圆转方、圆转圆)更为可靠，如传感器的安装位置，深度，粗细等因素对管道流体的影响。也可对不同的边界条件进行模拟，分析每个影响因素对管道流体的影响及计量的修正。

本节将以某一DN50的超声波流量计为例，分析热电偶的安装位置的影响及流量、温度对修正系数K的影响规律。

4.1 热电偶的安装影响

超声波热量表是在超声波流量计的基础上安装了热电偶监测进出口水温，一般说来，一个热电偶是安装在管道上，另一个是安装在超声波热量表预制好的接口。预制在超声波热量表的接口位置应该如何选取，不会影响超声波流量的测量，本节将对某一DN50的超声波热量表产品(结构和设计同上超声波流量计)进行模拟，分析其热电偶安装位置和深度对管道流体流动特性的影响(边界条件为：流量15 m3/h，流体温度25 ℃，其余同上)。

如图10所示，工质在圆截面管道中流动均一而稳定，在流道截面开始由圆转方时，由于流通面积逐渐减小而不断加速。进入方截面管道后，速度相对稳定，在即将离开方截面管道时，由于受到热电偶的影响，流通面积进一步降低，在热电偶的顶端，出现速度较大的区域，对超声波测量区域产生了较小的影响。同时，受热电偶的阻滞作用，热电偶前流体会出现低速区，热电偶对工质流动的干扰一直传递到下游。值得注意的是，热电偶不仅仅影响了下游的工质流动，扰动的范围已经蔓延到上游接近超声波探头附近，因此，如果热电偶的直径进一步增大或者热电偶的安装位置更靠近上游一些，会对DN50的测量结果产生难以忽视的影响。

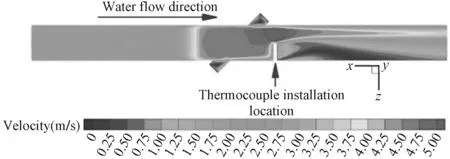
图10 流体域对称面速度分布

图11 局部放大显示的速度分布及流线分布

图11是对图10中所示流场的局部进行了放大，增加了流线的显示。如图11所示，流线在方截面管道中的流动整体较为平顺，但是在两个超声波探头的安装位置，由于尺寸突变而出现了两个稳定的驻涡，受主流的带动作用，两个驻涡的旋转方向一个为顺时针，另一个为逆时针。

图12是在热电偶长度的1/2位置所在平面，也增加了流线的显示。可见，受热电偶的扰流作用影响，下游区域存在一对对称的漩涡。不论是在超声波探头中产生的驻涡还是受热电偶扰流产生的漩涡，都会使流体的宏观动能在周而复始的旋转运动中通过流体微团之间的内摩擦和撞击而逐渐耗散掉，最终使得流动的流阻损失增大。建议在设计和工艺允许的前提下，尽量避免流通截面的突变，减小热电偶的影响，以减少漩涡产生进而减少流阻损失。

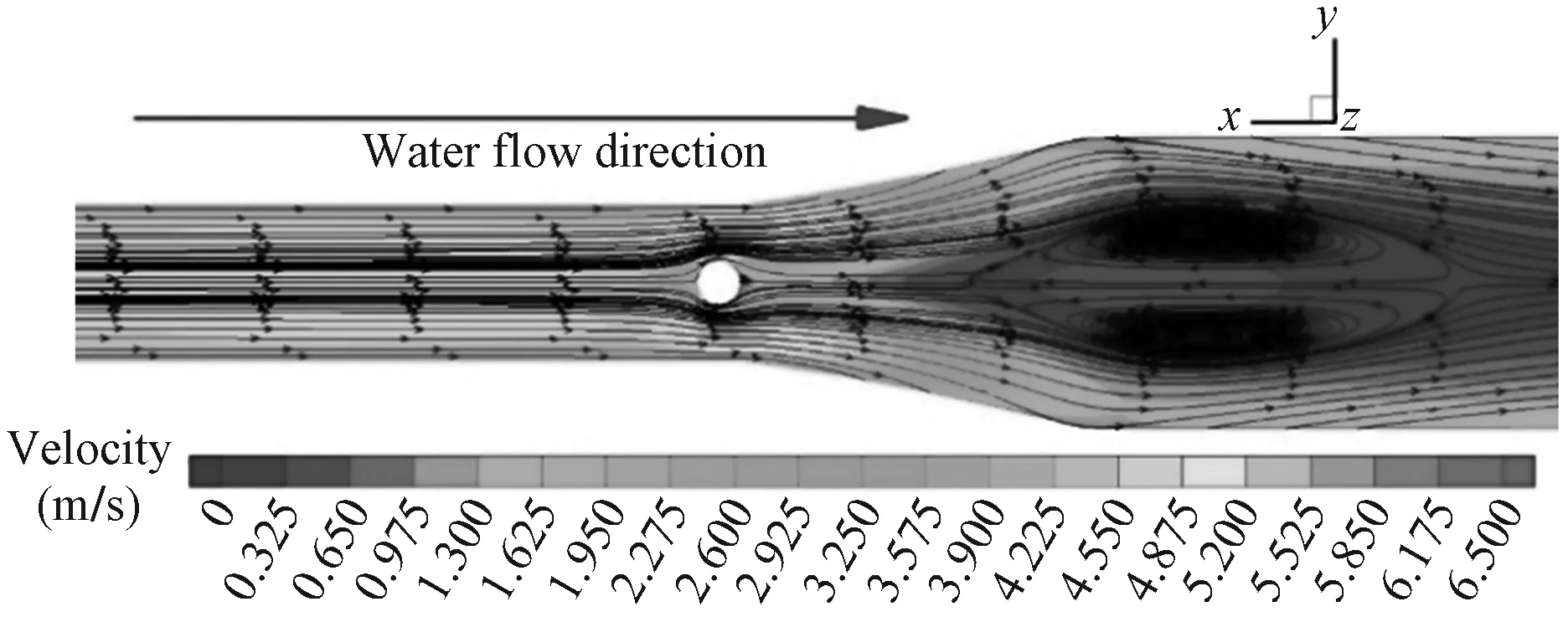
图12 热电偶对流动的影响

4.2 修正系数K变化规律

通过上文的实验数据和模拟结果，发现在同一温度下，修正系数K随着流量的增大而减小。为了了解同一流量下不同温度对修正系数K的影响，本节将通过模拟计算，得到同一流量下不同温度对修正系数的影响。

边界条件设置如下表所示，选取3种流量，4种温度(其余同上)，共12种工况，如表5所示，模拟计算得到12种条件下的修正系数K，分析变化规律。

表5 模拟的边界条件

在实际应用中，由于温度的变化导致水物性产生变化，进而导致的测量误差也不容忽视。图13给出了不同压力下黏度、密度与定压比热随温度变化，由图可知，水的定压比热与密度在不同压力下几乎保持恒定，在温度从30～90 ℃的变化范围内，比热的变化率约为0.56%，密度的变化率约为2.86%，而粘度的变化率达到了61.8%。

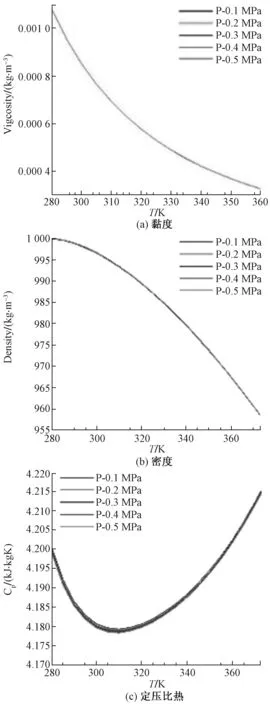
图13 不同压力下水定压比热、密度与粘度随温度变化

一般来讲，高精度热量计量装置的三个精度等级所允许的相对误差分别为1%、2%和3%。因此，定压比热随温度的变化可以忽略不计，而密度与粘度的变化不可忽略。因此，在计算不同温度下的工况时，必须考虑密度以及粘度随温度的变化。文献[12]中给出了密度随温度的拟合公式：

ρ(T)=-3×10-6T2-1×10-4T+1001

(15)

在计算流量与热量时，通过水的实时温度可以得到该工况下水的密度，进而提高热量表的精度。

考虑了温度对水的物性的影响，得到了0.15 m3/h 、0.6 m3/h与15 m3/h三种流量下，K系数随温度变化。如图14所示，当流量为15 m3/h时，K系数随温度变化很小几乎不变，而流量为0.6 m3/h 和0.15 m3/h时，K系数随温度有了明显的变化，随着温度的升高，先快速降低，再缓慢降低。当流量分别为15 m3/h、0.6 m3/h与0.15 m3/h时，温度从25～80 ℃变化，K系数随温度的最大变化率分别为0.38%、2.5%和5.8%。这表明，当流量较小时，流动本身因温度的变化所带来的测量误差已经超过了可接受的范围，因此可通过模拟的手段，对不同温度下的K系数进行修正。

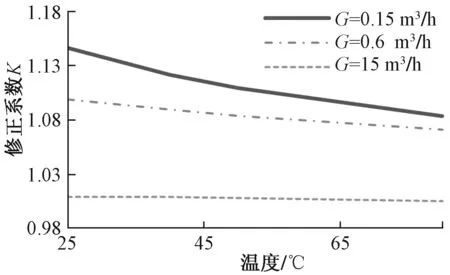
图14 三种流量下K系数随温度变化

5 结论

本文通过模拟的方法，对超声波计量表内部流场及速度分布进行了研究，并通过实验实测结果，验证了模拟仿真的可靠性。提出了模拟研究的方法，通过对模拟结果及一些定量计算结果进行分析之后，得到以下结论。

1)结论一：管道流量越小，修正系数K越大，随着流量的增大，修正系数K先快速减小，再缓慢减小并接近1，意味当流量越大时，流场分布更均匀稳定。

2)结论二：热电偶不仅仅影响了下游的工质流动，扰动的范围已经蔓延到上游接近超声波探头附近，因此，如果热电偶的直径进一步增大、长度进一步增长、或者热电偶的安装位置更靠近上游一些，或极端流量下，将会对该产品的测量结果产生难以忽视的影响。

3)结论三：当流量分别为0.15 m3/h 、0.6 m3/h与15 m3/h时，K系数随温度(25～80 ℃)的最大变化率分别为5.8%、2.5%和0.38%。当流量较小时，流动本身因温度的变化所带来的测量误差已经超过了可接受的范围，因此可通过模拟的手段，对不同温度下的K系数进行修正。

综上所述，影响测量精度的因素主要有两个：一是产品几何形状与热电偶的布置对流场的扰动，使得测点处的速度分布受到干扰，进而影响测量精度；二是在小流量下，温度的变化会对K系数的计算产生很大的影响，流动本身因温度的变化所产生的误差已经超过了精度等级要求的最大误差。因此，针对上述影响因素，给出相应的改进思路分别为：针对第一个因素，可以考虑优化热电偶设置的位置、角度和尺寸等，尽可能在满足加工工艺的前提下减少其对流场的干扰。针对第二个因素，在流量较小时需考虑温度的补偿。