一种改进的桥梁裂缝图像分割方法
2020-12-08段明义卢印举李祖照
段明义,卢印举,李祖照,苏 玉
(1.郑州工程技术学院 信息工程学院,河南 郑州 450044; 2. 广西交科集团有限公司,广西 南宁 530007)
0 引言
交通运输是经济发展的基本需要和先决条件,关系着国家经济的发展,承载着社会进步的命脉[1-2]。随着交通运输业的发展,我国每年都有新建道路投入使用,道路的养护工作变得十分重要。桥梁作为当今社会交通枢纽的重要组成部分,其投入使用后,随着时间的推移难免产生各种各样的损坏,裂缝是桥梁最常见的缺陷。裂缝检测是后续维护和修理的前提,是必不可少的工作。在实际工程中裂缝分布呈现无规律状态,同时,一般裂缝都比较细小,小于0.2 mm,容易被周围的障碍物等干扰从而形成漏检的安全隐患,因此对裂缝的检测要重点兼顾到细小裂缝。
图像分割是一种重要的图像处理技术。在对输入图像进行预处理之后[3-4],将预处理的结果进行划分,对每个划分后的子图像抽取它们各自的特征提取其中有价值的部分,从而完成识别和分析[5]。将图像分割技术应用到桥梁裂缝检测中[6]并与后续的其他方法相结合,从而迅速识别出裂缝以判定其危害程度,这对道路的安全保障及正常运行有十分重要的作用。长期以来,国内外学术界将图像分割方法运用到裂缝图像处理并取得了一些优秀的研究成果。迭代的阈值分割算法是在普通阈值分割算法的基础上进行了改进,该改进提高了性能,但阈值的手工设置是其一个突出的问题[7]。基于自适应阈值Canny裂缝检测算法不需要人工设置阈值,但对含有不均匀光照和噪声的图像其鲁棒性、稳定性较低。孙亮等[8]与多重滤波结合的Otsu算法虽然考虑到了不均匀光照,但其采用的阈值是单一的,限制了算法的适用性[9]。
裂缝图像特征数据分布不是高斯分布但可利用高斯函数近似拟合,因而高斯混合模型(Gaussian Mixture Model, GMM)[10]能够描述整幅图像的分布。K-means是目前在图像分割领域已经广泛应用的一种聚类划分方法[11],该方法通过对定义的目标函数进行迭代逼近,最终得到结果。其缺点主要在于需要事先人工设置、确定一系列的参数值,比如初始聚类数目,同时图像中的噪声也能大大地影响结果[12]。基于GMM 模型的聚类算法是一种改进的聚类方法,其基本思想是在利用GMM模型对图像拟合后,基于每个高斯混合概率将相应标签分配给每个观测值。然而由于初始点的选取具有随机性,其迭代过程的复杂度通常具有不确定性。
因此,根据上述分析,在本研究中为了分割桥梁裂缝图像,将裂缝图像像素点集架构为多层次高斯混合模型(Multi-Level Gaussian Mixture Model, ML_GMM),并在K-means算法聚类中心计算过程中引入合并阶段从而改进算法性能;同时,根据混合模型多重分解的思想[13-14]提出多级混合模型方法,将传统混合模型的每一个概率分布进一步再细分成单个概率成分;最后,利用期望最大化(Expectation Maximization, EM)算法[10]估算出未知参数的值,在得到感兴趣样本的混合模型分布后,根据最大后验准则确定像素所属的分类以完成裂缝图像分割。
1 方法
1.1 K-means聚类算法
令S={x1,…,xN}为裂缝图像像素点集,N为像素点数。算法主要步骤如下:
(1)设k=kinit,从S中随机抽样k个点{xμ1,…,xμk},分别将其作为聚类初始中心{μ1,μ2,…,μk}。初始时,kinit可以设为4。
(2)根据每个点到聚类中心的距离不同,将其分配到最近的聚类中心。
设Sj是距离μj最近的像素点集合(Sj⊆S),对于∀i≠j(1≤i,j≤k),∀x∈S,如果‖x-μj‖≤‖x-μi‖,有x∈Sj,nj为Sj中点数。
(3)如果nj<δ(δ为预定义聚类中点数阈值),则删除Sj。同时调整k的值,并用S1,…,Sk重新标记其余聚类。
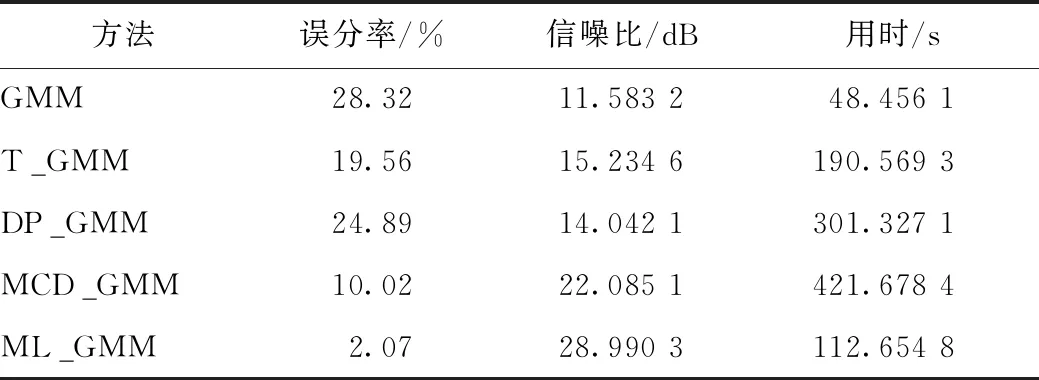
(5)计算各聚类中心{μ1,μ2,…,μk}两两间的距离dij=|μi-μj| (≤i (6)对步骤(5)中计算出的dij进行排序,对于聚类对(Si,Sj),如果dij<δd(δd为预定义类间距阈值),ni<δ,nj<δ(δ为预定义聚类中点数阈值)且Si和Sj在本次迭代中尚未参与合并,则合并聚类Si,Sj并用Sij=Si∪Sj替代它们,其加权平均值(niμi+njμj)/(ni+nj)作为合并后的聚类中心μij,重新标记其余聚类并相应地减少k值。 在桥梁裂缝的检测过程中,为实现裂缝图像的分割构建的高斯模型描述如下[10]: (1) 式中,期望矩阵μ是d维向量,方差-协方差矩阵∑是一个d×d的矩阵,det(·)为行列式。 如果在不同的聚类中都存在同一个类中的模式,这种情况下是不适合利用单个高斯模型去近似条件分布的。近似此类条件分布用高斯混合模型更适合,其定义为: (2) 式中,N(x;μ,∑)为一个期望为μ和方差协方差矩阵为∑的高斯模型: (3) θ=(w1,…,wm,μ1,…,μm, ∑1,…, ∑m)。 (4) 本研究在普通高斯混合模型的基础上将m个概率分布中的每个分布再进一步细分为n个概率成分,由n个成分拟合每个分布。表示如下: (5) 对于高斯模型: (6) 式中,θj,r=(μj,r,∑j,r),参数集θ=(μ1,1,…,μj,r, ∑1,1,…, ∑j,r);vj为属于第j个类别成分的权重;wj,r为属于第j个类别中第r个分布的权重。 在此,已经获得了采集到的样本数据的概率密度表达形式,对其中的未知参数θ的求解可以借助于EM算法,方法如下,从而最终得到感兴趣样本的混合分布模型。 EM算法是当输入x仅部分可观察的情况下,为了获得极大似然估计解而发展出来的。高斯混合模型的极大似然估计实际上也能被视为从不完全的数据中学习而来,并且EM算法能给出一种有效的方式来得到1个局部最优解。 该方法由E步和M步组成,基于必要条件来更新解并且交替计算辅助变量。具体步骤如下: (4)重复步骤(2)~(3)直到收敛。 感兴趣样本的混合分布模型得到后,接着可以计算每一个像素的后验概率。 (7) 利用最大后验准则[15],在每个像素的后验概率计算出来之后即可确定该像素xi所属的类别从而完成图像分割。 算法整体流程如图1所示。 图1 算法流程图Fig.1 Flowchart of algorithm 试验部分主要验证本研究所提出算法的运行性能,从两方面来衡量,即式(8)所定义的误分率和式(9)所定义的信噪比。 MCR=Ne/N×100%, (8) 式中,Ne为误分像素数;N为像素总数。从式(8)可以看出MCR的取值范围为[0,1],其值越小表示分割结果越好,该指标主要表征图像错误分割部分所占的比例。 PSNR=10lg[(2n-1)2/MSEX,Y], (9) 式中,n为图像中像素比特数,一般取值8。对于图像X和Y,若一个为另一个的噪声近似,则MSEX,Y表示两者间的灰度均方误差。该指标用于评价图像分割结果抗噪能力的大小,其值越大表示分割结果抗噪能力越强。 试验主要在仿真图像和实际采集到的裂缝图像上进行,本研究方法为多层次高斯混合模型法(ML_GMM),对比算法包括传统高斯混合模型法(GMM)、阈值高斯模型法(T_GMM)[16]、密度峰值高斯混合算法(DP_GMM)[17]以及最小化协方差矩阵法(MCD_GMM)[18]。 为了验证本研究所提出的分割算法,在试验部分,构建以Matlab 2012b为基础的测试环境。硬件平台主要指标为:8 GB内存以及英特尔酷睿3.2 GHz CPU。 2.2.1仿真图像 通过绘图软件Photoshop来完成仿真图像的生成,如图2(a)、3(a)所示。 (1) 本次试验主要验证椒盐噪声对各算法的影响。椒盐噪声通过函数生成(密度为0.02)并添加在图2(a)中形成图2(b)。各算法的运行结果分别如图2(c)~2(g)所示。 图2 椒盐噪声分割结果Fig.2 Salt and pepper noise segmentation result 从图2可以得出,与传统高斯混合模型相比阈值高斯模型法(T_GMM)与最小化协方差矩阵法(MCD_GMM)在抗噪方面提高很多,但阈值高斯模型法(T_GMM)分割出的图像不如最小化协方差矩阵法(MCD_GMM)分割出的图像清晰,而密度峰值高斯混合算法(DP_GMM)分割出的图像更清晰,但其抗噪能力不如阈值高斯模型法(T_GMM)与最小化协方差矩阵法(MCD_GMM)。而本研究所提出的多层次高斯混合模型法(ML_GMM)无论是在抗噪方面还是图像清晰度方面,都优于其他几种算法。 表1给出了各方法的定量评估结果。分析表1可知,本研究算法的两项指标均优于其他几种算法。由于后4种算法都是在传统高斯混合模型法(GMM)的基础上进行了改进,这4种算法因为其含有更加复杂的运行步骤,故而运行所消耗的时间比传统高斯混合模型法(GMM)要多。 (2) 本次试验主要验证高斯噪声对各算法的影响。高斯噪声通过函数生成(均值为0,方差为0.02)并添加在图3(a)中,形成图3(b)。各算法的运行结果分别如图3(c)~3(g)所示。 表1 椒盐噪声定量评估结果Tab.1 Salt and pepper noise quantitative evaluation result 图3 高斯噪声分割结果Fig.3 Gaussian noise segmentation result 从图3可以得出,与传统高斯混合模型相比阈值高斯模型法(T_GMM)、密度峰值高斯混合算法(DP_GMM)以及最小化协方差矩阵法(MCD_GMM)都能够分割出更加清晰的图像。在抗噪方面,密度峰值高斯混合算法(DP_GMM)比阈值高斯模型法(T_GMM)以及最小化协方差矩阵法(MCD_GMM)表现更好一些。最小化协方差矩阵法(MCD_GMM)虽然能分割出更加清晰的图像,但其抗噪性能不如阈值高斯模型法(T_GMM)以及密度峰值高斯混合算法(DP_GMM)。而本研究所提出的多层次高斯混合模型法(ML_GMM)不仅能分割出清晰的图像而且能够有效抑制噪音。 表2给出了各方法的定量评估结果。分析表2可知,本研究算法的两项指标均优于其他几种算法。由于后4种算法都是在传统高斯混合模型法(GMM)的基础上进行了改进,这4种算法因为其含有更加复杂的运行步骤,故而运行所消耗的时间比传统高斯混合模型法(GMM)要多。最小化协方差矩阵法(MCD_GMM)在误分率方面更接近本研究算法,阈值高斯模型法(T_GMM)在耗时方面更接近本研究算法。 表2 高斯噪声定量评估结果Tab.2 Gaussian noise quantitative evaluation result 2.2.2裂缝图像 本研究试验用到的裂缝图像是通过桥梁检测车在实际桥梁路段采集得到,如图4(a)所示。运行各个算法得到图4(b)~4(f)所示的结果。 图4 裂缝图像分割结果Fig.4 Crack image segmentation result 从分类结果(图4(b)~4(f)可知,阈值高斯模型法(T_GMM)比传统高斯混合模型法(GMM)在抗噪方面提升了很多,但还有噪声残留;密度峰值高斯混合算法(DP_GMM)能够抑制一定的噪声;最小化协方差矩阵法(MCD_GMM)的抗噪能力非常强,但在一些明显部位的去躁效果不佳,比如中间上方部位的噪音;本研究提出的多层次高斯混合模型法(ML_GMM)的分割效果(图4(f))相比于其他几种算法,在抗噪方面有明显的提升,能够分割出清晰的裂缝图像,同时能够把噪声最大化地去除。 定量对比结果如表3所示。 分析表3可得出,本研究算法ML_GMM的两项评价指标误分率和信噪比都优于其他方法,但其在耗时方面不是最优的,这主要是因为该方法相对于传统高斯混合模型法(GMM)以及阈值高斯模型法(T_GMM)来说较复杂,为了达到良好的分割效果多消耗了运行时间。 试验表明,本研究方法可以取得更好的图像分割结果并且抗噪能力更强。 本研究针对桥梁裂缝检测问题提出了一种新的裂缝图像分割方法。该方法在采用期望最大化算法的基础上从两方面进行改进:针对裂缝图像分割的特点改进了传统的K-means算法,在聚类中心计算过程中引入合并阶段从而改进算法性能;提出多级混合模型方法,将传统GMM的每一个概率分布进一步再细分成单个的概率成分从而提高图像分割的效果。通过以上两个方面的改进,本研究得到了比使用传统K-means算法和普通GMM的分割方法抗噪能力更强、精度更高、效果更好的分割结果。
1.2 高斯混合模型GMM
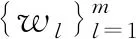
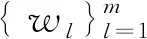
1.3 EM算法
1.4 后验概率
1.5 算法流程图

2 试验结果与分析
2.1 分割效果评价准则
2.2 试验结果与分析




3 结论
