音圈电机设计优化与分析

潘新远 常以涛 张长胜 钱俊兵

（1.云南锡业股份有限公司铜业分公司；2.昆明理工大学a.信息工程与自动化学院；b.民航与航空学院）

音圈电机是一种简单的机电式直线电机，作为一种电磁驱动能量转换器，在电机、航空及流体控制系统等领域有着广泛的应用［1］。 音圈电机由永磁体和电流驱动的电磁线圈组成，是一种小型化的直线或旋转驱动技术。 音圈电机满足空间或质量限制应用中的运动控制要求，例如在移动摄影中作为照相机镜头的执行器［2］，在医疗应用中作为左心室辅助设备［3］和呼吸机中的阀门控制［4］。更普遍地说，音圈电机已广泛应用于各种领域，如汽 车悬架［5］、纳米光 刻 和 计量 学［6］、激 光 雷达应用的光色散［7］、通用快速转向镜［8］和硬盘驱动器［9］。音圈电机的工作原理基于洛伦兹力定律，它将电流直接转化为运动，而不需要中间形式的能量转换［10］。 音圈电机具有结构简单、体积小、响应快、速度高、加速度高及控制简单等优点，广泛应用于高精度定位运动系统中［11～13］。

现代生产中经常需要高精度的快速响应直线运动。 如果用带机械传动的旋转马达来实现直线运动， 机械传动会产生齿隙和较大的摩擦力，而音圈电机是一种直接驱动电机，它使用永久磁场和线圈绕组产生与施加到线圈绕组的电流成比例的力［14，15］，其固定部分为永磁体，运动部分为线圈绕组。

迄今为止，一些学者对音圈电机的性能提升已做出了较大的贡献。 胡永珊等考虑到三维精密运动平台存在模型不确定性和扰动不确定性，提出采用鲁棒控制算法，并验证了其较好的效果［16］。 Encica L等研究了磁路部分结构参数对静态电磁力的影响［17］。吴帅等采用永磁Halbach阵列在每个冗余音圈电机中简化系统结构，并基于解析磁路模型采用粒子群优化方法对设计参数进行优化，同时Halbach阵列可以消除磁干扰［18］。 这些结果表明：某些结构参数对音圈电机中的磁场分布有显著影响。

1 结构设计

由于音圈电机应用场合的多样化，不同场合的音圈电机有不同的设计要求。 根据文献［19，20］， 一般来说音圈电机的设计应遵循以下基本原则：

a. 以最少的永磁体和导磁材料设计具有高磁通密度的均匀气隙磁场，提高工作效率，产生尽可能大的推力。

b. 在满足推力要求的前提下，尽量减小音圈直线电机的体积和运动部分的质量，使它具有更高的加速度和更快的响应能力。

在精密仪器中，音圈电机是作为作动器直接安装于仪器中使用的。 精密机电系统要求音圈电机具有小安装尺寸、高推力常数及低热扩散等特殊的性能。 在优化设计中，为了实现音圈电机小安装尺寸、高推力常数，除了采用高磁密度的永磁体外， 还必须考虑对电机结构进行优化设计。音圈电机的结构参数对线圈的电磁力有很大的影响。 为了获得良好的性能，必须适当地指定这些参数。 基于有限元分析方法，对电机的驱动电流、励磁机高度、气隙及阻尼孔尺寸等主要参数进行了分析。 当电磁力在磁场中作用于带电线圈时， 其方向可以根据安培定律的左手定律来确定。 因此，可以通过调节通电电流的方向和值来控制音圈电机的线圈上下移动。 施加在线圈上的电磁力F表示为：

式中 B——磁通密度；

I——电流；

L——线圈有效长度；

N——线圈匝数。

在永磁体的磁场中，磁场的能量分布于整个磁场空间，磁场空间内单位体积的磁能表示为：

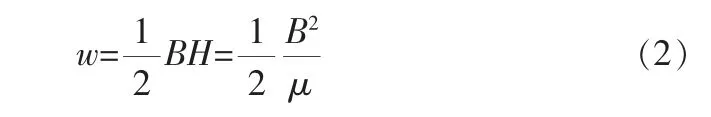
式中 B——磁感应强度；

H——磁场强度；

w——磁场空间内单位体积的磁能；

μ——磁场空间中介质的磁导率。

由式（2）可知，在磁感应强度一定的磁场空间中，介质的磁导率μ介越大，相应的介质空间磁场的储能的密度就越小，反之亦成立。 在音圈电机的磁场介质中，磁轭的磁导率远大于空气的磁导率，因此，音圈电机中的气隙存储了永磁体磁场绝大多数的磁能，即永磁体磁场的磁能主要消耗于音圈电机的气隙中。

1.1 传统结构

传统矩形音圈电机的结构如图1所示， 在电机永磁体的磁力线回路中， 只有一块永磁体，即一块永磁体对应一个气隙磁场。

1.2 改进结构设计

笔者提出一种针对精密机电设备的改进音圈电机结构（图2）。 为了便于和传统的结构进行对比，在永磁体的材料和尺寸、磁轭的材料和厚度、气隙的高度方面，改进的音圈电机都与传统的音圈电机一致。

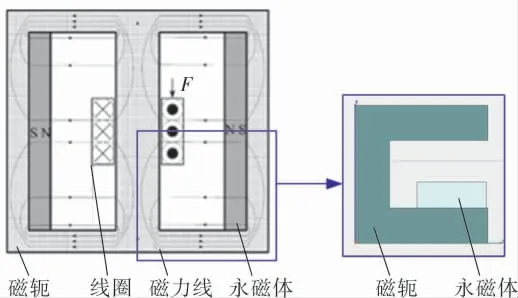
图1 传统矩形音圈电机结构

图2 改进的音圈电机结构

如图2所示，在改进的音圈电机结构中，每一磁力线回路经过2个磁场气隙和4块永磁体。 可以看出每一气隙对应2块永磁体， 对比传统的音圈电机结构，改进结构利用有限的空间提高气隙的磁感应强度，从而获得更大的电机推力常数。 另外，动子线圈的结构设计应确保线圈两受力边的中心位置位于上下永磁体覆盖的中心。

2 计算与仿真

电机电磁场数值计算是对电磁场的积分和微分方程进行离散化， 形成线性代数方程组，并对线性代数方程组进行求解，以获得电磁场的近似解。 电机电磁场的二维交变电场求解器所满足的复数拉普拉斯方程如下：

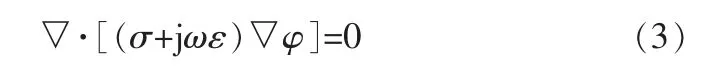
式中 σ——介质的电导；

ε——介电常数；

ω——激励角频率；

φ——标量电位。

电机电磁场的二维静磁场求解器所满足的非齐次标量波动方程如下：

式中 A——磁位矢量；

J——电流密度矢量。

电机电磁场的二维涡流场求解器所满足的波动方程如下：

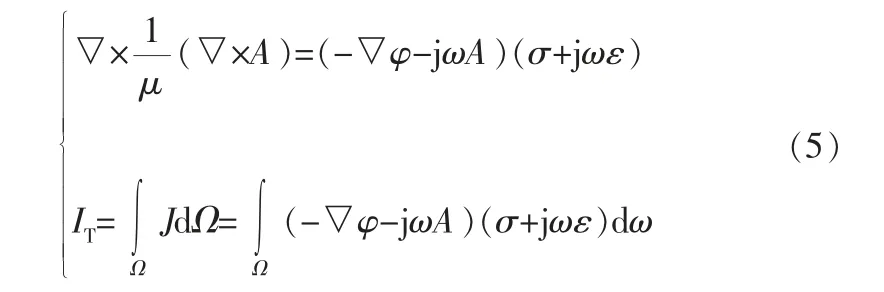
式中 IT——流过导体的总电流；

Ω——导体横截面域。

电机电磁场的二维轴向磁场求解器所满足的齐次波动方程如下：

图3 传统音圈电机磁场仿真结果

为进一步验证改进音圈电机结构的可行性及其相比于传统音圈电机结构的优势， 笔者采用Ansoft进行了仿真实验， 图3为传统音圈电机磁场仿真结果， 图4为改进结构音圈电机磁场仿真结果。 由图3a和图4a中磁力线分布可知，传统音圈电机磁力线分布相比改进结构音圈电机磁力线分布更稀疏，因此新结构音圈电机磁场较强，进而可获得较大的扭矩， 同时新型音圈电机磁力线分布相比传统音圈电机磁力线分布更为均匀； 由图3b和图4b磁场云图可知，新型音圈电机磁场更均匀、对称，可以较好地遍及整个区域，因此新型音圈电机相比于传统音圈电机在工作时更为稳定，同时避免电机对壳体的冲撞，进而降低电机损耗。

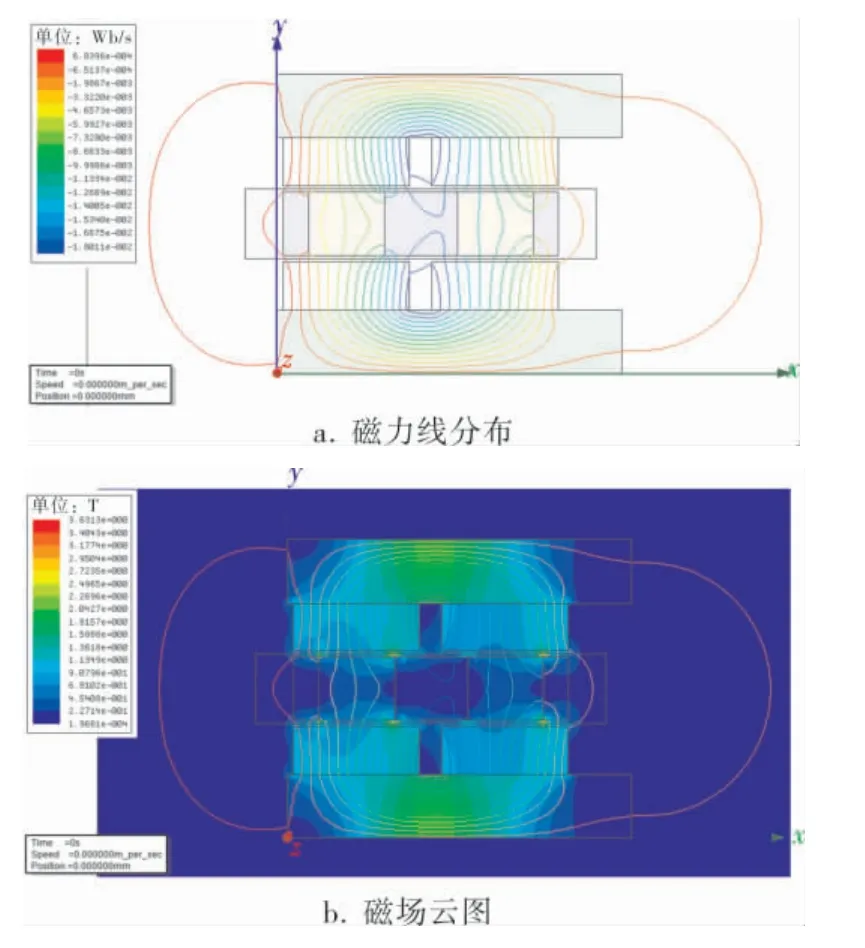
图4 改进结构音圈电机磁场仿真结果

现在用电磁场仿真对比分析两种模型结构，以进一步确定新模型的优点。 分别对两种模型进行有限元的建模分析（图3、4）。 在图中，两种音圈电机拥有相同的永磁体尺寸、磁轭厚度和气隙尺寸。 比较两种模型气隙磁场的有限元仿真结果可知，改进结构模型的气隙磁感应强度比传统模型的气隙磁感应强度分布更加均匀、集中，而且气隙磁感应强度也明显得到很大提高。 这就意味着，在上述同等条件下，改进结构模型的推力常数要高于传统模型的推力常数。

改进的音圈电机结构模型的磁通回路充分利用了两个线圈的气隙作为磁通路。 因为导磁钢的磁导率远大于空气的磁导率，为了有效避免永磁体磁场的能量浪费于非线圈的气隙，传统音圈电机结构模型就需要利用导磁钢作为磁轭建立专门的磁通通路。

3 结果与讨论

图5、6分别为传统音圈电机和改进结构音圈电机在相同工况条件（线圈电流10A，速度0m/s，位移0m）之下，各自的电磁推力曲线、电机反电动势曲线和相绕组磁链曲线。 由图5a、6a可知，传统音圈电机的电磁推力曲线在上升阶段出现超调，0.00～0.02ms内电磁推力变化范围为623.840 80～623.842 52N， 变 化0.001 72N， 后 续 稳 定 在623.842 42N，而改进结构音圈电机的电磁推力曲线相对较稳定，未出现超调，在0.00～0.02ms内电磁 推 力 变 化 范 围 为-1.343 196 ～-1.343 178kN，变化0.000 018kN， 后续稳定在-1.343 178kN；由图5b和图6b电机反电动势曲线可知，传统音圈电机 反 电 动 势 在0.00 ～0.02ms 内 变 化 范 围 为0 ～170mV，最大反电动势为170mV，改进结构音圈电机反电动势在0.00～0.02ms 内变化范围大致为-280～0mV，最大反电动势绝对值为280mV；由图5c和图6c相绕组磁链曲线可知，传统音圈电机相绕组磁链在0.00～0.02ms内变化范围为1.749 678 0～1.749 681 3Wb，变化0.000 003 3Wb，后续稳定在1.749 681 3Wb，改进音圈电机相绕组磁链在0.00～0.02ms内变化范围为0.718 583 1～0.718 588 8Wb，变化0.000 005 7Wb，后续稳定在0.718 588 8Wb。

图5 传统音圈电机的仿真曲线

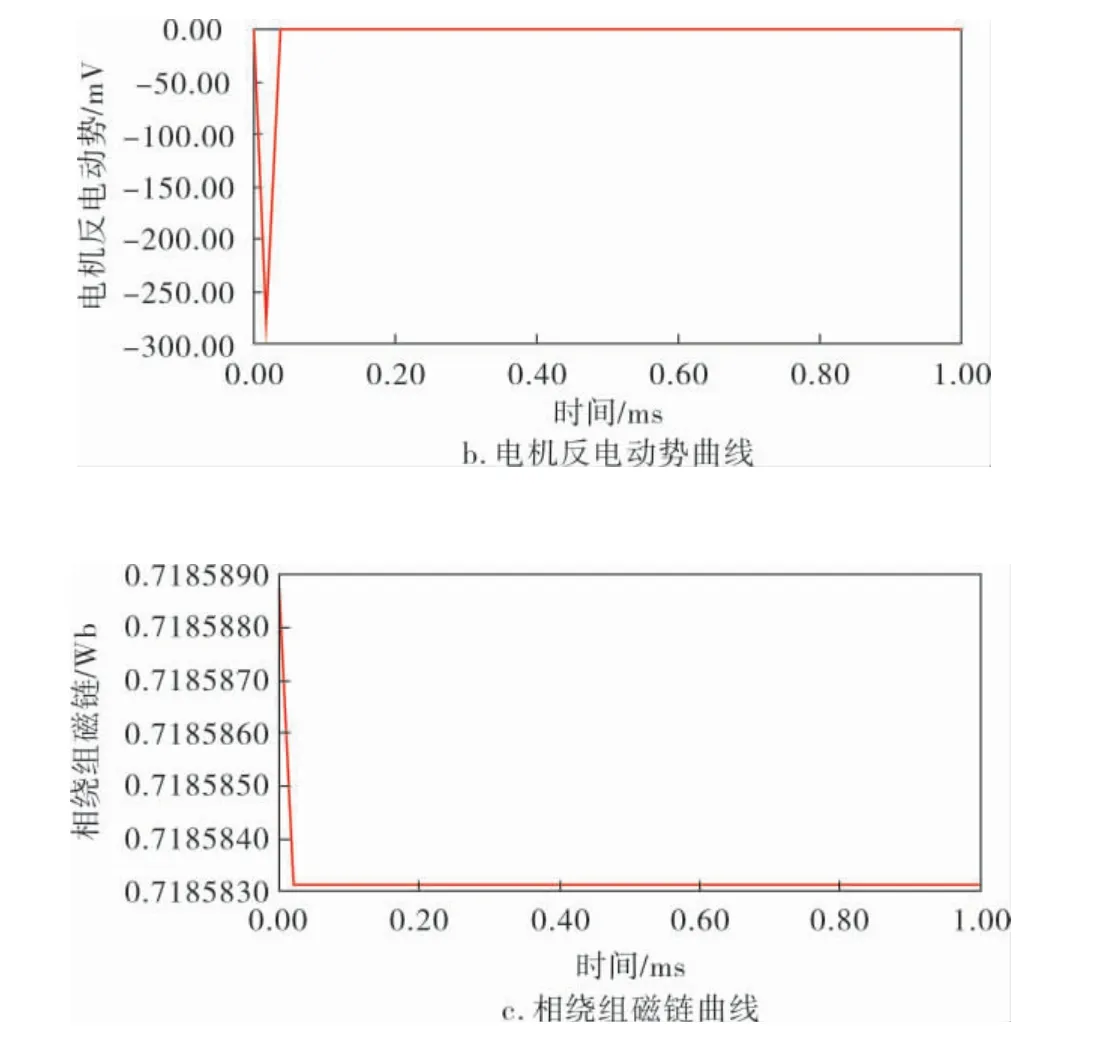
图6 改进结构音圈电机的仿真曲线

综上所述，改进电机模型比传统电机模型有着更加紧凑的结构，能更有效地利用永磁体的磁场能量于线圈气隙，从而使音圈电机的线圈气隙磁感应强度在小体积情况下得到有效的提高；改进电机模型比传统电机模型推力常数大。

4 结束语

针对传统音圈电机气隙磁场磁感应强度不足的问题，设计了一种改进的气隙磁感应强度结构，在传统音圈电机的基础上通过增加永磁体使得有限的空间气隙可获得更强的磁感应强度，进而提高电机的推力常数， 最后通过Ansoft电磁仿真软件对所提改进结构进行仿真，并将仿真结果与传统音圈电机在电磁推力、电机反电动势和相绕组磁链3方面进行比较， 结果表明所提改进结构均有良好性能。