无砟轨道不平顺对行车安全性影响的可靠性分析

2020-12-08李再帏雷晓燕

铁道学报 2020年10期

李再帏，雷晓燕，高亮

(1.上海工程技术大学城市轨道交通学院，上海 201620；2.华东交通大学铁路环境振动与噪声教育部工程研究中心，江西南昌 330013；3.北京交通大学土木建筑工程学院，北京 100044)

轨道不平顺是高速铁路无砟轨道养护维修的重要工作，其状态直接关系轨道结构在役服役性能，并对列车运行的安全产生直接影响。为了保证无砟轨道服役安全性，铁路管理部门对轨道不平顺控制从幅值与波长两个方面展开，即通过控制几何形位幅值限值[1]与轨道不平顺谱[2]来有效地实现轨道状态管理。但鉴于轨道不平顺具有显著平稳随机特性[3]，其结构函数无法用明确解析式进行表达，使得上述两种方法无法定量地表征高速列车行车安全的可靠性。因此，从轨道不平顺随机特性出发，研究轨道不平顺对高速列车行车安全性的影响并明确相关的敏感性因素就显得尤为重要。

现有国内外研究往往基于随机振动理论、轮轨动力理论、时频分析理论、结构可靠性理论等探究轨道不平顺对高速行车的安全性影响，如文献[4]分析了轨道随机不平顺在不同列车运行速度下轨道随机振动响应特性，确定了相应随机变量的统计分布类型；文献[5]通过建立列车-板式无砟轨道-路基动力学模型，讨论了轨道短波随机不平顺对轮轨系统动力学响应的影响；文献[6]利用VAMPIRE动力学软件，分析了不同类型的轨道随机不平顺对300 km/h高速列车运行平稳性和安全性的影响，确定了影响列车平稳性的激扰源；文献[7]建立轮轨动力学模型，通过输入随机轨道不平顺，研究了不同速度和线路条件下脱轨系数功率谱密度动力学分布特性；文献[8]利用Wavelet-Wigner-Hough时频理论和轮轨动力学模型，分析了轨道随机不平顺对轮轨系统服役可靠性的影响；文献[9]采用响应面和Simpack动力学模型相结合的方法，研究了轨道随机不平顺对列车运行安全性的影响。这些研究对提高轨道结构役服役安全性起到了极大的促进作用，有力保障了高速列车运行品质。但值得注意的是，上述研究多是从定性的角度出发对相关因素影响进行研究，缺乏定量描述；而目前对结构服役安全的定量分析往往是通过结构可靠度来实现的，且在无砟轨道结构部件损伤分析[10]、弹条疲劳性能失效分析[11]、轨道板横向稳定性[12]等研究中得到了一定的应用。

基于此，本文利用结构可靠度的相关理论方法，将响应面法与轮轨动力学理论相结合，通过建立相应的结构失效极限状态方程，研究无砟轨道不平顺对高速行车安全性的影响，从而实现定量地对轨道不平顺状态进行评估。

1 列车运行安全性的极限状态

在轮轨系统中轨道结构服役状态失稳的特征表现形式较多，如轨道主体结构(轨枕、道床、底座板、轨道板等)承载力不足失稳，脱轨系数和轮重减载率失稳等。由于既有高速铁路无砟轨道结构设计的偏安全性，使得在使用限期内的结构主体一般均可满足承载力的设计要求。因此，轮轨系统的状态失稳多呈现轮轨动力失稳的特征，即可以通过相关的轮轨动力学评估指标来确定列车运行安全状态。现行国内外标准中，脱轨系数和轮重减载率是主要的安全评价指标[13]，所以，本研究中将这两个指标作为列车运行安全性评价的主要标准。

根据相关标准和文献[9,14]，本文对轨道结构服役极限状态定义进行界定：轮轨系统的一部分超过某一特定状态就不能满足相关铁路设计规范的车辆-轨道系统安全行车的要求，该特定状态即为极限状态。

极限状态实质上是列车运行安全状态的一个阈值，在该阈值以内，处于安全而可靠的状态；反之，若超过这一阈值，则处于不安全和失效的状态。

如果用随机向量X=(X1,X2,…,Xn)表示影响列车运行安全的n个基本随机变量，用Z=g(·)表示列车运行安全状态功能函数为

(1)

式中：“极限状态”所对应的Z=g(X)=0为极限状态方程。若对应脱轨系数和轮重减载率两个评判准则有两种失效状态对应的列车运行安全性极限状态方程为

(2)

(3)

由式(2)和式(3)可知，这些功能函数受诸多因素影响(轨道不平顺、外界环境等)，无法得到相应的显示解析表达式，这就意味着无法进行相应的积分梯度运算来确定失效概率，因此，本文采用响应面与轮轨动力学模型相结合的方法进行状态函数的隐式化研究。

2 响应面法原理与极限状态方程求解

2.1 基本原理

响应面法(Response Surface Methodology, RSM)为解决极限状态方程形式隐式化问题提供了一种可靠的建模及计算方法，其基本思想是对于隐式或需要耗费较多时间才能确定实际功能函数或极限状态面，用一个相对方便应用的显式函数(称为响应面函数)代替，其基本算法如下[15]：

(1) 选择包含不交叉项的二次多项式响应面作为响应函数为

(4)

式中：a,bi,ci为二次多项式的未知系数。

(2) 选取抽样中心点xM=(x1,x2,…,xn)T，围绕中心点利用试验设计方法选取试验点，即围绕抽样中心点选取2n+1个试验点如下：

(5)

(6)

(3) 计算2n+1个抽样点处功能函数值，计算第k次迭代时式(4)中二项式的待定系数，进而确定出第k次迭代时响应面模型的显示表达式。

(5) 反复执行式(2) ～式(4)，直到前后两次计算所得可靠指标之差|β(k)-β(k-1)|<εβ，εβ为预先给定的收敛准则，一般为0.000 1。

2.2 模型建立与求解

由式(2)和式(3)可知，需进行轮轨动力学计算，本文采用的模型为有限元法建立列车-无砟轨道-路基耦合动力学模型，相关的模型推导与验证见文献[1]，采用交叉迭代法进行系统动力学响应求解。

由于高低不平顺和轨向不平顺是轮轨作用力的主要来源，且两者呈现不相关的关系[13]，因此，本文将此两种不平顺作为轮轨系统的输入参量，轮轨力作为输出参量，将其代入极限状态方程中，采用响应面法进行求解，从而确定列车运行安全性。计算流程如图1所示。

图1 模型的计算流程

具体计算方法为：

(1)根据实测轮轨系统激励源数据(高低不平顺和轨向不平顺)，计算样本统计特征(均值、方差和概率密度函数)。

(2)将不平顺样本均值作为中心点，利用中心复合点法，生成不平顺样本值，计算相应的轮轨动力学响应。其中，f值采用自适应性调整的方法。为了涵盖每个随机变量的绝大多数信息，应用工程中的3σ原则，因此，第一次迭代计算时f取为3。为了减小样本宽度对迭代收敛速度的影响，从第二步起f值取为1。

(3)采用式(4)作为响应面函数来逼近列车运行安全极限状态方程，利用一次二阶矩法计算可靠性指标β和最可能失效点MPP。

3 模型验证与分析

3.1 算例

为了对本文所提分析方法进行验证，这里采用如下算例：

高速列车为标准CRH3型动车组、运行速度为350 km/h，轨道结构为CRTSⅡ型双块式无砟轨道，基础为路基结构，相关的参数值详见文献[1]。

轨道不平顺实测样本为0号高速综合检测车所测某高速铁路线路数据，典型区段的检测结果时域波形如图2所示。

图2 轨道不平顺时域分布

采用中心线高低不平顺和轨向不平顺作为样本输入，则相应的实测样本时域统计特征计算结果如表1所示。

表1 不平顺统计检验与分布参数

由表1可知，轨道不平顺在置信度0.05下，符合高斯分布，可利用其对相应不平顺的概率密度函数进行描述。

将轨道不平顺的统计特征值代入到响应面与轮轨动力耦合中，得到的轨道结构服役安全性计算结果，如表2所示。

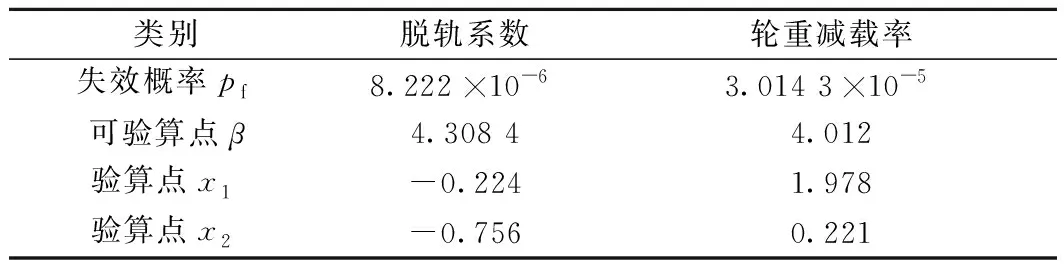
表2 RSM计算结果

根据GB 50216—2019《铁路工程结构可靠性设计统一标准规范》[14]可知，CRTSⅡ型板式无砟轨道属于铁路工程结构安全等级中的二级，对应的目标可靠度指标建议管理值为3.7即失效概率为1.078 ×10-4，则表2中所得的区段样本满足可靠性技术标准的要求。

对比高速铁路无砟轨道动态几何不平顺管理值[16]可知，最有可能失效点区间为[0, 2]mm即为350 km/h线路轨道Ⅰ级峰值管理值。

除了改善生态环境、塑造绿带景观外,环城绿带植物群落的功能也需随着城市更新而不断丰富和完善。上海市绿化局牵头研究编辑的《上海市绿道专项规划》[4]中提到计划在2020年于环城绿带百米林带内建设绿道,供市民进行日常活动。近年来,人们休闲娱乐需求日益增长,环城绿带百米林带因其区位条件好、消费成本低、交通便捷,将成为居民日常休闲活动的最佳去处[5]。然而目前针对上海环城绿带植物群落的研究中,尚缺乏对于植物群落与游憩的相关研究。

3.2 模型验证与分析

蒙特卡洛法(Monte Carlo Simulation，MCS)在样本足够大的情况下，可以有效地逼近非线性系统的解析解[15]。因此，本文这里采用MCS进行验证求解，从而对上述计算结果进行验算。相应的计算流程见图3。

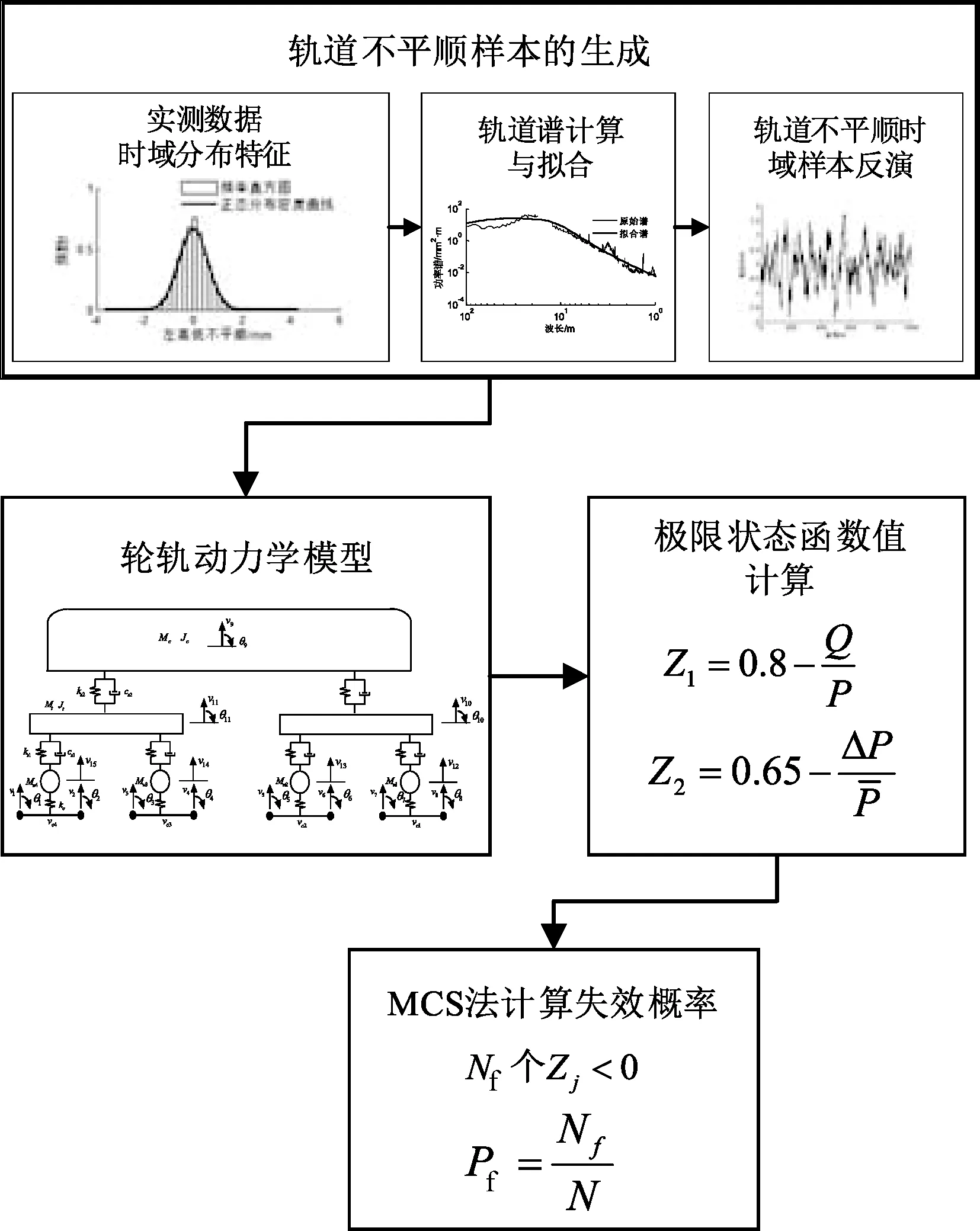
图3 MCS法计算求解流程

利用图2中实测的轨道不平顺样本进行轨道谱拟合，利用得到的拟合参数进行时域波形反演。将轨道不平顺时域样本作为激励源输入到轮轨动力学模型中，计算相应的轨道结构服役失效概率及可靠性指标。若要使得靠指标β满足规范[14]的可靠度指标要求，则至少要进行1×105以上的次数，本文这里选取计算次数为1×105。则，得到的计算结果见表3。

表3 MCS计算结果

由表3可知，利用MCS方法得到的计算结果与表2相比差距很小，其误差可以满足工程计算的精度要求，这说明了利用响应面法求解列车运行安全极限状态方程的准确性。

值得注意的是，由于本文轮轨动力学采用有限元方法，在形成轨道单元和车辆单元时，虽已经进行了相关的优化计算，但矩阵求逆仍需耗费大量时间。因此，进行一次1×106的MCS法机时巨大，一般为9.48×108s。而采用响应面法求解时，虽一般只需进行数十步迭代即可满足可靠度指标的收敛条件，但每次动力学响应迭代计算仍需耗费大量的机时，一般为4.93×104s。所以，进行MCS方法计算时间为RSM方法的1.92×104倍。

综上分析，可知采用响应面方法可以有效地实现列车运行安全极限状态方程的求解，所得到结构的失效概率和可靠度指标与蒙特卡洛法得到的近似解析解相比较，符合度极高，说明了本文所提方法的有效性与准确性。