谨防“勾股”中的“雷区”

文 孙媛媛

同学们在解决与勾股定理相关的问题时，多多少少会触碰到一些“雷区”。下面我们就来举例说明，希望同学们能理解定理，仔细审题，规范答题，知错防错，有效“避雷”，在勾股定理的世界自由翱翔。

雷区一 不讨论斜边引起的漏解

例1一个直角三角形的两边长分别是3和4，则该直角三角形的第三边长为_____。

【错解】5。

【错因分析】同学们对我们祖先留下的“勾3，股4，弦5”印象深刻，一拿到这题，往往很顺利地就想到两条直角边长分别为3、4，第三边长为5。我们来回顾一下勾股定理：直角三角形的两直角边的平方和等于斜边的平方，而题目仅仅给出两边，显然没有明确已知边的“角色”。同学们错解的原因就是把已知边默认为直角边。所以，当情况不明确时，我们必须分类讨论，以防漏解。我们知道，直角三角形中斜边最长，所以3不可能是斜边长，但是，4可能是斜边长。所以当4为斜边长时，直角三角形的第三边长。

【正解】5或。

雷区二 不清楚概念引发的多解

例2若一个三角形的三边分别是a、b、c且a、b、c为一组勾股数，其中a=3，b=4，则c=_____。

【错解】5或。

【错因分析】在遭受雷区一的“轰炸”后，同学们会自觉地考虑多种情况了，然而，又不知不觉陷入另一个“雷区”——勾股数。何为勾股数？勾股数是指构成直角三角形三边的一组正整数。显然这里有两个条件，一是两条较短边的平方和等于第三边的平方，二是a、b、c都为正整数。显然错解中的不符合条件。

【正解】5。

雷区三 不判定图形形状

例3如图1，在四边形ABCD中，∠D=90°，AD=2，CD=2，BC=3，AB=5，求四边形ABCD的面积。

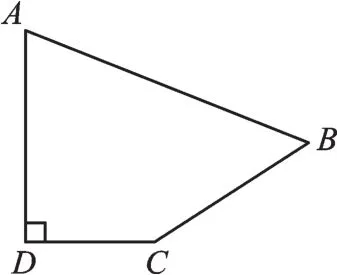
图1

【错解】如图2，连接AC。

在△ADC中，∵∠D=90°，

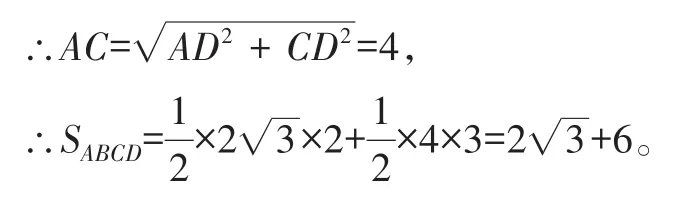
图2

【错因分析】有的同学在求得AC后，没有判定△ABC的形状，默认了△ABC是直角三角形，直接求面积。这里同学们应该运用勾股定理的逆定理来证明△ABC是直角三角形。

【正解】如图2，连接AC。

在△ADC中，∵∠D=90°，

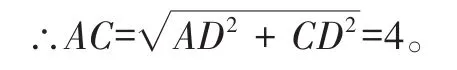
在△ABC中，AC=4，BC=3，AB=5，

则有BC2+AC2=32+42=25，AB2=52=25，即BC2+AC2=AB2，

∴∠ACB=90°，△ABC为直角三角形，

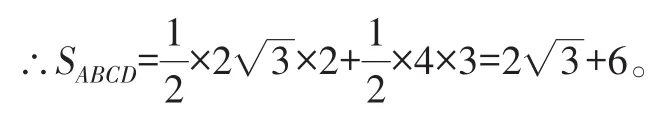
雷区四 凭直觉造成的误解

例4如图3，梯子AB靠在墙上，梯子的底端A到墙根O的距离为0.7m，梯子的底端A向外移动到A′，使梯子的底端A′到墙根的距离等于1.5m，同时，梯子的顶端B下降至B′，求BB′的长（梯子AB的长为2.5m）。

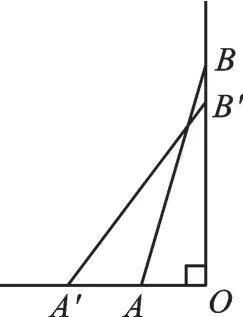
图3

【错解】BB′=AA′=1.5-0.7=0.8m。

【错因分析】有的同学只凭直觉，认为梯子下降多少，就等于梯子往左滑动多远，即BB′=AA′。这是不对的，凡事都要有理有据。我们可以亲自拿个梯子进行实地试验，BB′与AA′并不相等。正确的做法应该是先求OB和OB′，再得到BB′的长。

【正解】根据题意，可得AB=A′B′=2.5，∠AOB=90°，在△ABO中，AO=0.7，AB=2.5，∠AOB=90°，

在△A′B′O中，A′O=1.5，A′B′=2.5，∠A′OB′=90°，

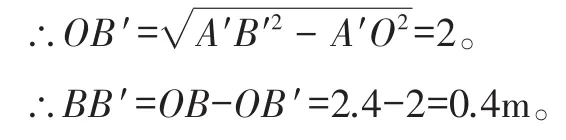
答：BB′的长为0.4m。