一种空间曲线轨迹跟踪的无人机自适应导航控制算法
2020-12-08郑积仕孟凡茹赖宏图陈兴武
郑积仕,孟凡茹,赖宏图,陈兴武
(福建工程学院 信息科学与工程学院,福州 350118)
0 引言
无人机可以根据预先设定的航线自主飞行,广泛的应用于军事巡逻、资源勘探、地形勘测等,随着无人机应用越来越广泛[1-2],飞行任务越来越复杂,如目标跟踪、自主着陆[3]、编队飞行[4]、空中加油[5]和利用空气动力学进行发电[6]等,这也对无人机空间轨迹跟踪控制算法提出更高的要求。
目前,三维轨迹导航控制算法是研究的热点[7],其中,文献[8]中提出了利用特殊正交群SO(3)求解姿态问题的三维路径跟踪算法,文献[9]中基于Lyapunov理论设计三维路径跟踪导航算法,通过控制目标路径航点的速度来避免最接近无人机投影点作为参考点所引起的奇异性,并且适用于平滑条件一般的三维曲线。文献[10-11]中构建一个矢量场,使无人机沿着矢量场收敛到期望路径,并且在风的干扰下也有很好的跟踪性能。其中矢量场算法中矢量场组合中有死区,并且无人机每次到达段的末端,矢量场会改变[12]。文献[13-14]中提出的L1-Navigation非线性导航算法应用较为广泛[15]。L1-Navigation导航算法在预期轨迹上选择一个参考点,参考点与无人机之间的距离为L1,并且通过参考点产生一个横向加速度指令,控制无人机飞行,在直线路径跟踪上采用PD控制,沿着曲线轨迹跟踪加入了超前量,并且横向加速度指令中使用惯性速度,在由外部干扰的情况下速度可以自适应变化[13]。目前L1-Navigation导航算法已经在Ardupilot开源软件中被应用,但L1-Navigation导航算法存在参数固定、自适应能力不强等缺点。
本文以空间八字曲线导航为例,空间八字空间曲线是通过两个半圆以及两个测地线构成,通过空间曲线上的目标航点以三维坐标的形式表示,无人机当前位置的目标航点坐标乘以旋转矩阵表示下个目标航点坐标。将导航控制分为横向、速度高度控制,通过两个固定增益系数来计算加速度,由于增益系数不变,在固定翼无人机实际飞行时,受到外界干扰无法自适应变化,导致无人机会产生一定的轨迹误差。
轨迹误差是导航控制的重要指标,本文采用自适应的方法优化控制性能,减少轨迹误差。模糊控制结合人的经验,无需构建精确的控制模型,适用于导航控制性能的优化上。本文以计算横向加速度的增益系数为输出量,根据变化的轨迹误差来调整常数系数,从而改变加速度的大小,优化固定翼无人机在空间曲线飞行的轨迹误差,提高跟踪性能和控制的自适应性。
本文的结构安排如下:第二部分构建空间曲线模型,以空间八字曲线为例。第三部构建模糊自适应控制器,以轨迹误差和轨迹误差变化率作为模糊控制输入量,计算横向加速度的增益系数常数作为输出量,优化控制效果。第四章对提出的优化方案进行模拟飞行测试,经软件在环仿真测试,验证了本文方法的有效性。最后是本文的总结。
1 空间曲线飞行导航控制
本文以空间八字曲线为例,固定翼无人机绕着空间八字曲线周期飞行利用空气动力学将风能转换成电能进行发电[6],固定翼无人机在空中飞行发电相比于传统发电机大大降低了安装塔架的成本[16]。在半球上的周期八字曲线如图1所示。
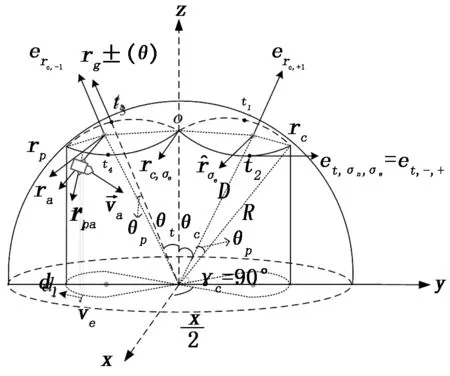
图1 在球上的八字曲线周期飞行路径
1.1 空间八字曲线
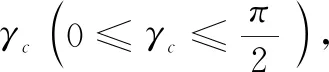
在图1中八字空间曲线有四个段组成,分别是东西方向的两个小圆段(转弯圆),两个大圆段(简称测地线,在xoy的平面投影为直线),其交点为交叉点o,四个过渡点(测地线与小圆段的交点)分别是t1、t2、t3、t4。转弯圆的半径Rc=Rsinθρ,θt转弯圆的圆心与Z轴的夹角。在NED坐标下垂直空间曲线的路径平面的单位法向量erc如公式(1)所示[6]。指向东西(σe=±1)转弯圆的圆心的单位法向量如公式(2)所示。
(1)
球心到转弯圆圆心的距离D=Rcosθρ,并且球心到转弯圆的圆心的位置向量rc=Derc。
(2)
两个测地线相交的夹角为χo(0<χo≤π),并且东方向两个测地线与转弯圆相交的过渡点t1、t2的位置向量如公式(3)所示:
(3)
东北、西北、东南、西南四个方向的过渡点的单位切向量如公式(4)所示。
(4)
其中:(σn,σe)=(+,+),(+,-),(-,+),(-,-)。
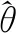
(5)
(6)
空间八字曲线飞行上的点都是绕着y轴旋转-θ角,绕着z轴旋转ψ角,结合以上公式,可以推出空间曲线的旋转矩阵R(θ,ψ)=(eθ,eψ,-er),其中在NED坐标系下单位向量如公式(7)~(9)所示。
(7)
(8)
(9)
e1,e2为横向平面子空间的基向量。
(10)
1.2 导航控制
导航控制分为(NE空间)横向平面的导航控制和速度高度控制[16]。导航控制决定了无人机的横向加速度和滚转角的大小。空间曲线上点的位置向量r(φ)如图1所示,公式如下。
R(cosθρerc+sinθρ(cosφeθc+σsinφeψc))
(11)
(12)
其中空间曲线上点的位置向量分为(NE空间)横向平面位置向量和高度位置向量,如公式(13)~(14)所示。
r1(φ)=(Rcosθρsinθce1+
sinθρ(cosφcosθce1+σsinφe2))
(13)
z(φ)=-R(cosθρsinθc-cosφcosθρsinθc)
(14)
从而可以得出曲线上一点的横向速度v1(φ):
(15)
则无人机的向心加速度为a1(φ),其中k1(φ)为曲线的曲率[6]。
(16)
无人机在飞行过程中,实际飞行路径与预期轨迹存在一定的轨迹误差,在图1中无人机的位置向量为ra,无人机的横向平面投影点为ve,预期轨迹上距离无人机最近点的位置向量rp,如公式(17)所示,其中enp为最近点的外部法向量。
rp=Derc+Rsinθρenp
(17)
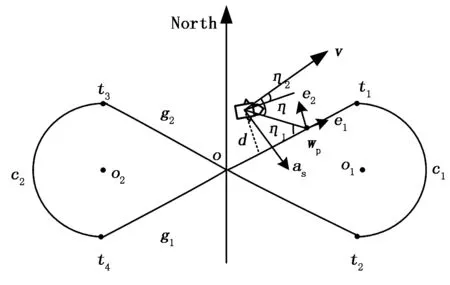
图2 八字飞行路径横向平面投影
三维空间中轨迹误差向量为rpa=ra-rp,轨迹误差在横向方向的投影向量rpal=rpa-rpa,3e3,其中rpa,3e3为纵轴方向,横向投影的轨迹误差如公式(18)所示:
dl=sgn(rpalenpl)|rpal|
(18)
速度向量在横向方向的投影以及速度矢量在法线方向的分量如公式(19)所示。
vpal=va-va,3e3,Vl=vpalenpl
(19)
结合运动学方程得出无人机在空间曲线上飞行过程的加速度如公式(20)所示,其中Kr和Kv为增益系数。
ap=a1+Krdl+KvVl
(20)
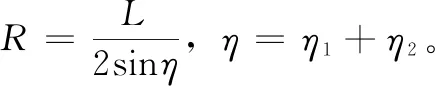
(21)
本文的导航控制方法已经成功在ardupilot中实现,代码中将无人机在跟踪空间曲线飞行时加速度分为两种情况:
1)无人机在在空间曲线外飞行或进行跟踪直线飞行,轨迹误差向量横向投影dl大于零a=as。
2) 无人机在曲线内飞行,轨迹误差向量横向投影dl小于零a=ap。
2 三维曲线跟踪的自适应导航控制
无人机在空中飞行可能会遭受外部环境的干扰(风的干扰),无人机受风的干扰轨迹误差增大,所以须考虑环境干扰下的自适应性以及跟踪性能。
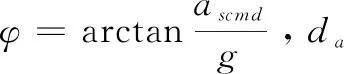
通过公式(21)和(22))可以发现无人机的加速度与增益系数Kr和Kv,L1-Navigation导航中的增益系数KL1有关:
(22)
其中:T是周期,周期不改变Kr也固定不变。通过改变常数系数k1与k2,增益系数Kv和KL1随之改变。根据图3、图4与表1所示,通过更改常数系数k1,k2,空间八字曲线轨迹变化,轨迹误差也随之改变。所以本文设计一个双输入单输出的模糊控制系统,如图3所示,以轨迹误差(e)和轨迹误差变化率(de)为输入量,并且以常数系数k=k1,k2(u)为输出量,根据变化的轨迹误差来调整常数系数k,从而改变加速度的大小,减小固定翼无人机在空间曲线飞行的轨迹误差,优化曲线路径。
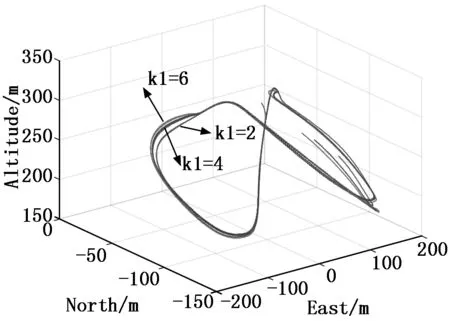
图3 增大k空间曲线路径
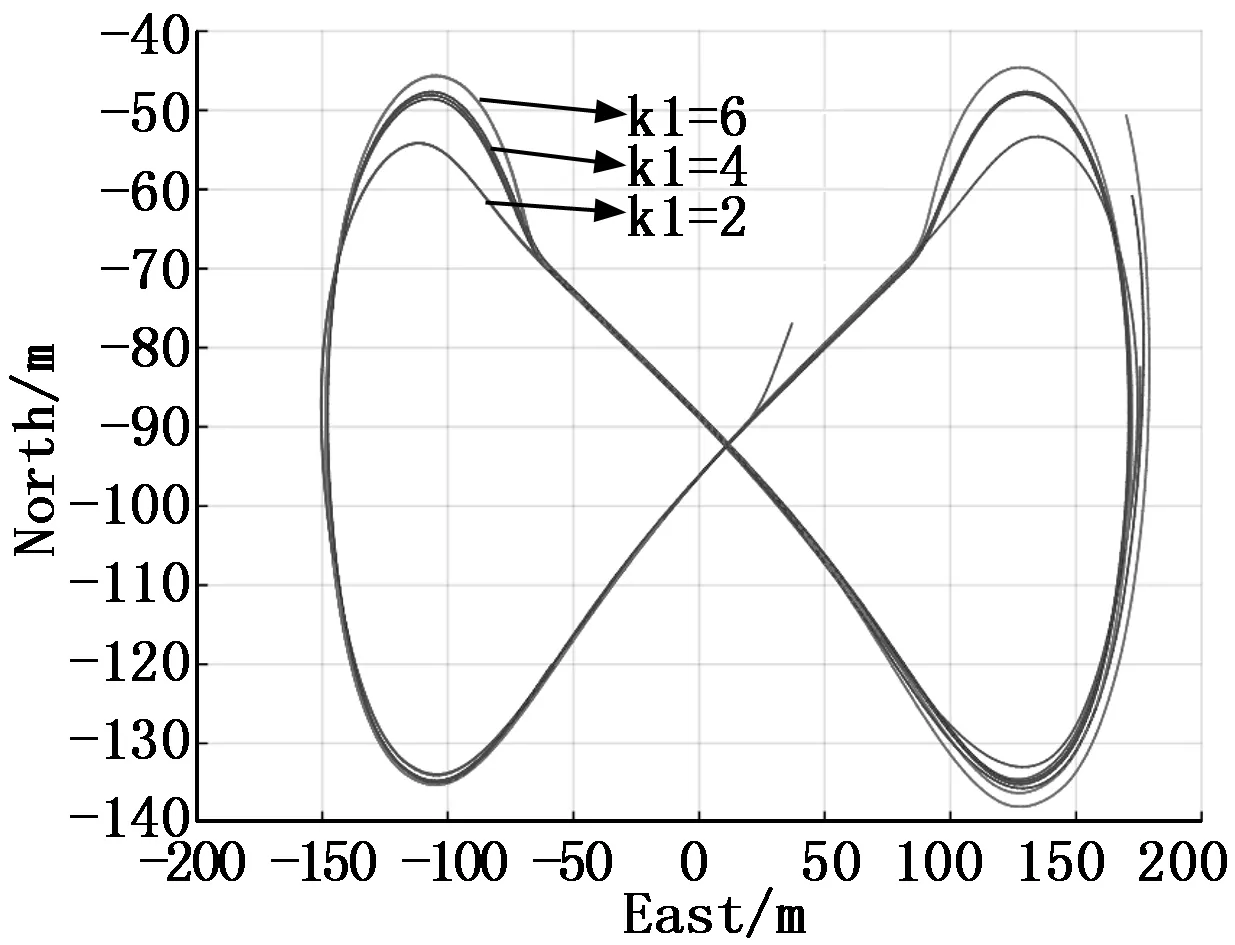
图4 横向平面投影

表1 轨迹误差根方差
2.1 选择模糊变量
经多次仿真测试,本文中轨迹误差e的物理论域为[-200,200](单位m),模糊论域为[-3,3]。轨迹误差变化率的物理论域为[-200,200](单位m),模糊论域为[-3,3],其中轨迹误差、轨迹误差变化率的量化因子Ke=0.015,Kde=0.015。
常数系数k的物理论域u有两种情况:
1)当无人机在空间八字曲线内飞行:
常数系数k1(u)的物理论域为[1,4],模糊论域为[-3,3],常数系数k1的比例因子Ku=0.833。
2)当无人机在空间曲线外飞行、跟踪航点:
常数系数k2(u)的物理论域为[4,8],模糊论域为[-3,3],常数系数k1的比例因子Ku=0.333。
轨迹误差e和轨迹误差变化率de都有七个模糊子集为[-3,-2,-1,0,1,2,3],用字母表示分别是NB(误差负最大),NM(误差负中),NS(误差负小),ZO(误差为零),PS(误差正小),PM(误差正中),PB(误差正最大),轨迹误差e的三角形隶属度函数如图5所示。常数系数u有七个模糊子集为[-3,-2,-1,0,1,2,3],用字母表示分别是NB(系数最小),NM(系数越小),NS(系数小),ZO(系数适中),PS(系数大),PM(系数越大),PB(系数最大)。
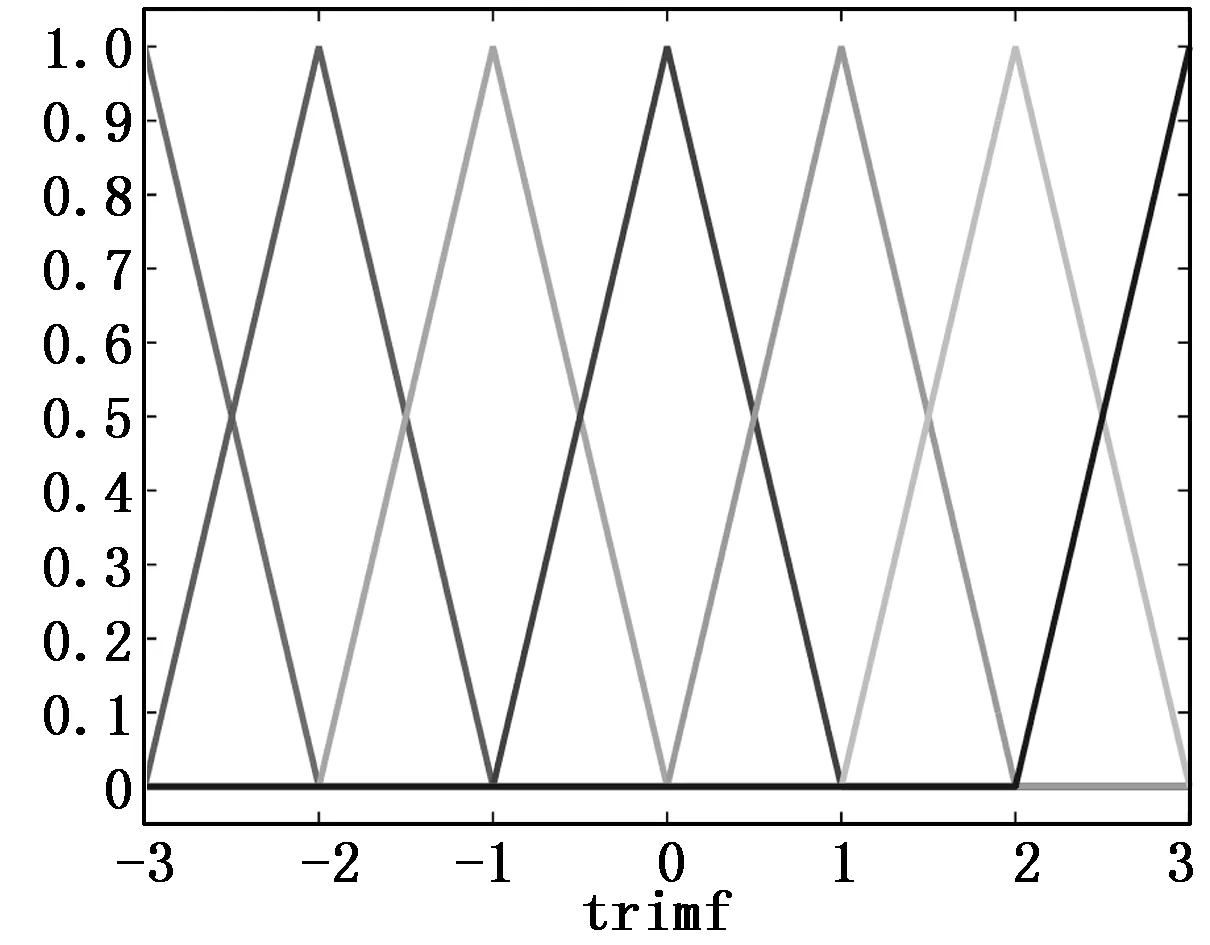
图5 轨迹误差e三角形隶属度函数
在跟踪预期轨迹的过程中,与预期轨迹之间出现误差,需要快速响应调整误差,所以模糊变量隶属函数采用三角形隶属函数,输出变量的去模糊化采用面积中心法,面积中心法是隶属度函数曲线与横坐标包围面积的中心[17],这个中心所对应的横坐标就是要求的输出变量。如公式(23)所示,其中A(uj)是u在第j点隶属度函数。
(23)
2.2 模糊规则的设定
模糊规则是模糊系统重要的组成部分[18],本文有49条模糊规则,是经过多次实验和经验所得,如表2所示。
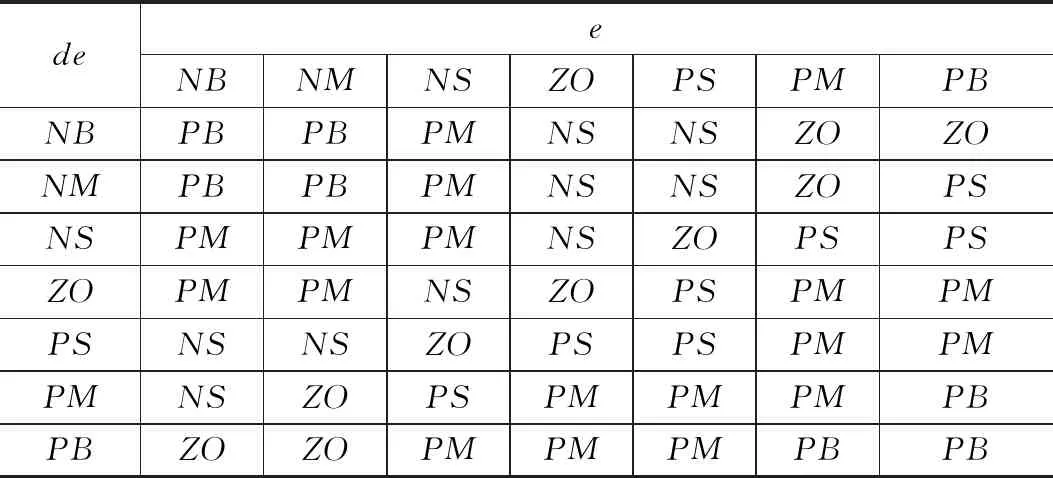
表2 模糊规则表
表中两个输入量分别是轨迹误差e和轨迹误差变化率de,当轨迹误差|e|越大,误差变化率|de|大的时候,KL1增益系数就越大,当轨迹误差和误差变化率基本为零时,KL1增益系数适中,模糊规则例如下:
If e is NM and de is Z0 then u is PM;
If e is Z0 and de is PM then u is PM;
….
If e is PS and de is NS then u is Z0;
If e is PM and de is PS then u is PM.
3 仿真实验
为了验证本文的方法的有效性,本文基于开源自动驾驶仪Ardupilot平台进行SITL(Software in the Loop)仿真,Ardupilot是全球应用最广泛的开源平台之一[19],SITL可以在没有硬件的情况下进行模拟飞行,可以实时修改飞行导航代码,进行编译模拟飞行,避免无人机在真实环境中损坏。本文使用小型固定翼无人机3.10版本固件,无人机的飞行数据来自飞行模拟器中的动力学模型[20]。本文利用飞行数据闪存日志(logs)中的数据在Matlab中进行图像显现,仿真实验飞行设定无人机飞行速度为22m/s,飞行实验主要有两个测试:无干扰条件下的空间曲线轨迹跟踪仿真测试,干扰条件下空间曲线跟踪仿真测试(固定翼无人机跟踪空间八字曲线代码已经上传到github中[21])。
3.1 无干扰条件下空间曲线轨迹跟踪仿真
为了验证使用模糊控制可以改进空间曲线飞行的轨迹误差和优化空间曲线路径,本文将为空间曲线飞行轨迹和使用模糊控制改进的空间曲线飞行轨迹进行对比,图6为无人机跟踪空间八字曲线模拟飞行轨迹,如图7和图8所示。
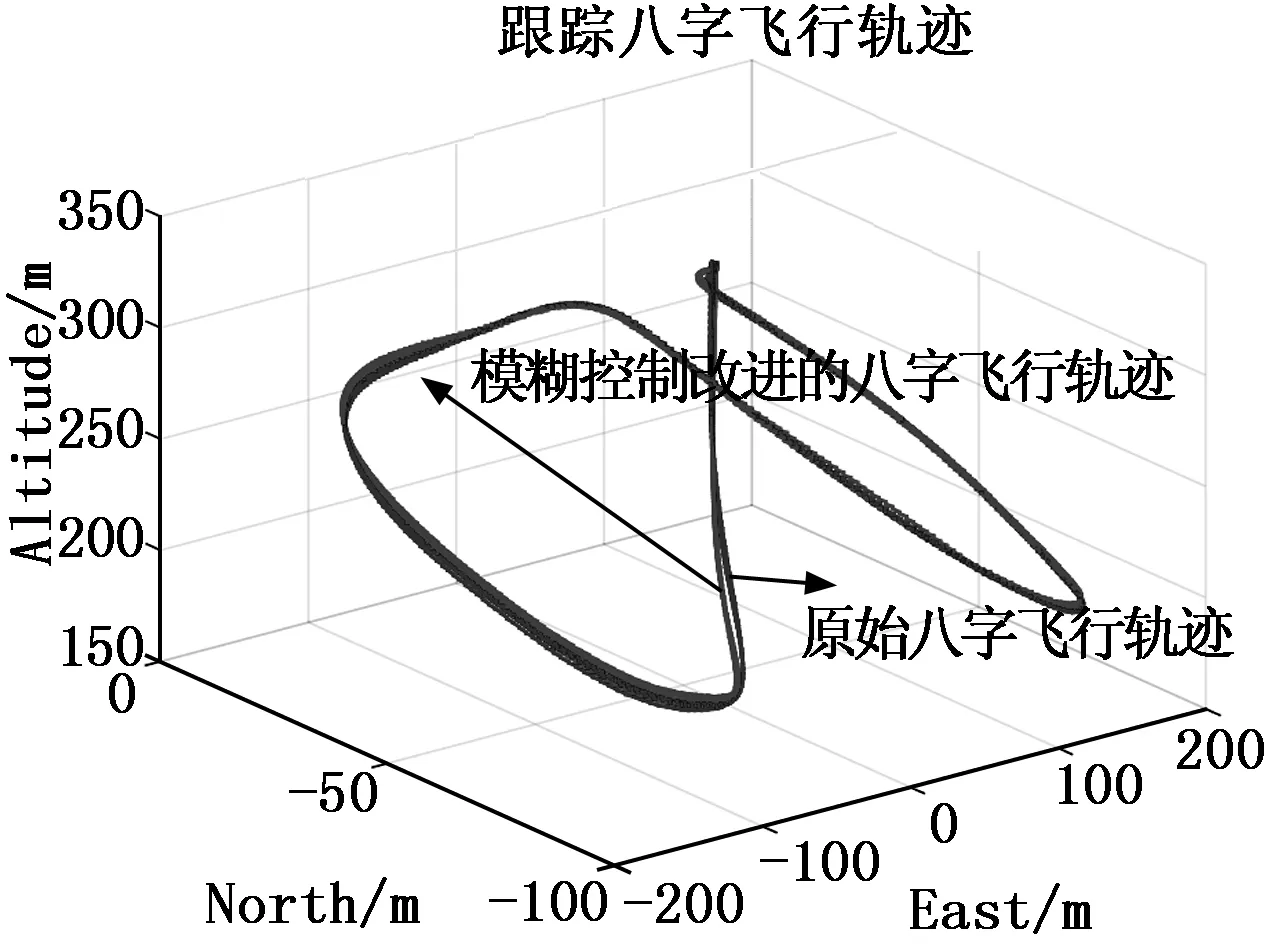
图7 无干扰条件下空间曲线飞行轨迹
无人机在八字曲线内飞行,轨迹误差增大时,常数系数k1增大修正轨迹误差;若无人机在八字曲线外飞行跟踪目标航点,当轨迹误差增大时,常数系数k2增大,修正轨迹误差。如图6为无人机模拟飞行,图7为空间曲线轨迹,图8为八字曲线轨迹的横向投影。从表3中可以看出使用模糊控制改进的导航算法跟踪八字曲线轨迹相比于原导航算法的曲线轨迹估计误差均方根小,曲线更加规则化,并且更接近预期轨迹。
3.2 干扰条件下空间曲线跟踪仿真
为了验证改进空间曲线飞行算法的实用性,在有风干扰的条件下进行仿真测试,风速10 m/s,风向西风。图9为风干扰下三维曲线轨迹,图10为风干扰下横向平面投影。
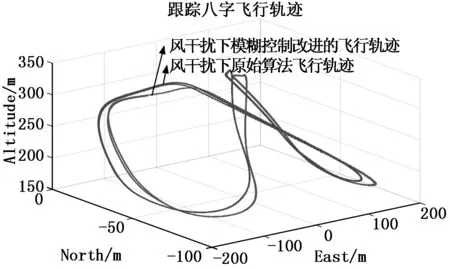
图9 风干扰下三维曲线轨迹
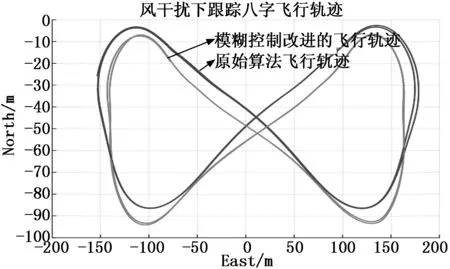
图10 风干扰下横向平面投影
无人机在常风的干扰下跟踪八字曲线轨迹,如图11所示,曲线轨迹往风向侧偏移,其中原始导航算法下,无人机跟踪的八字曲线轨迹相比于使用模糊控制改进的导航算法偏离的比较大。
如图12所示,利用模糊控制改进的导航算法在风干扰的情况下可以自适应的修正飞行轨迹,使无人机沿着设定轨迹飞行。如图13轨迹误差变化对比,利用模糊控制改进的导航控制算法相比与原始导航算法,轨迹误差变化比较平缓。从图12、13中对比说明添加模糊控制有很好的自适应性,根据轨迹误差的变化自适应的调整常数系数k,减小轨迹误差,从而说明有良好的跟踪效果和鲁棒性。
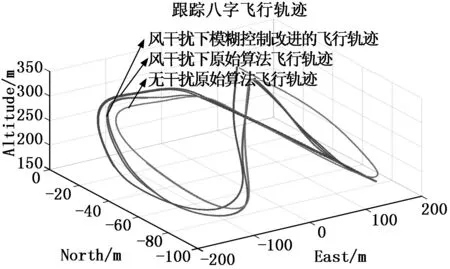
图11 三种情况下飞行轨迹对比
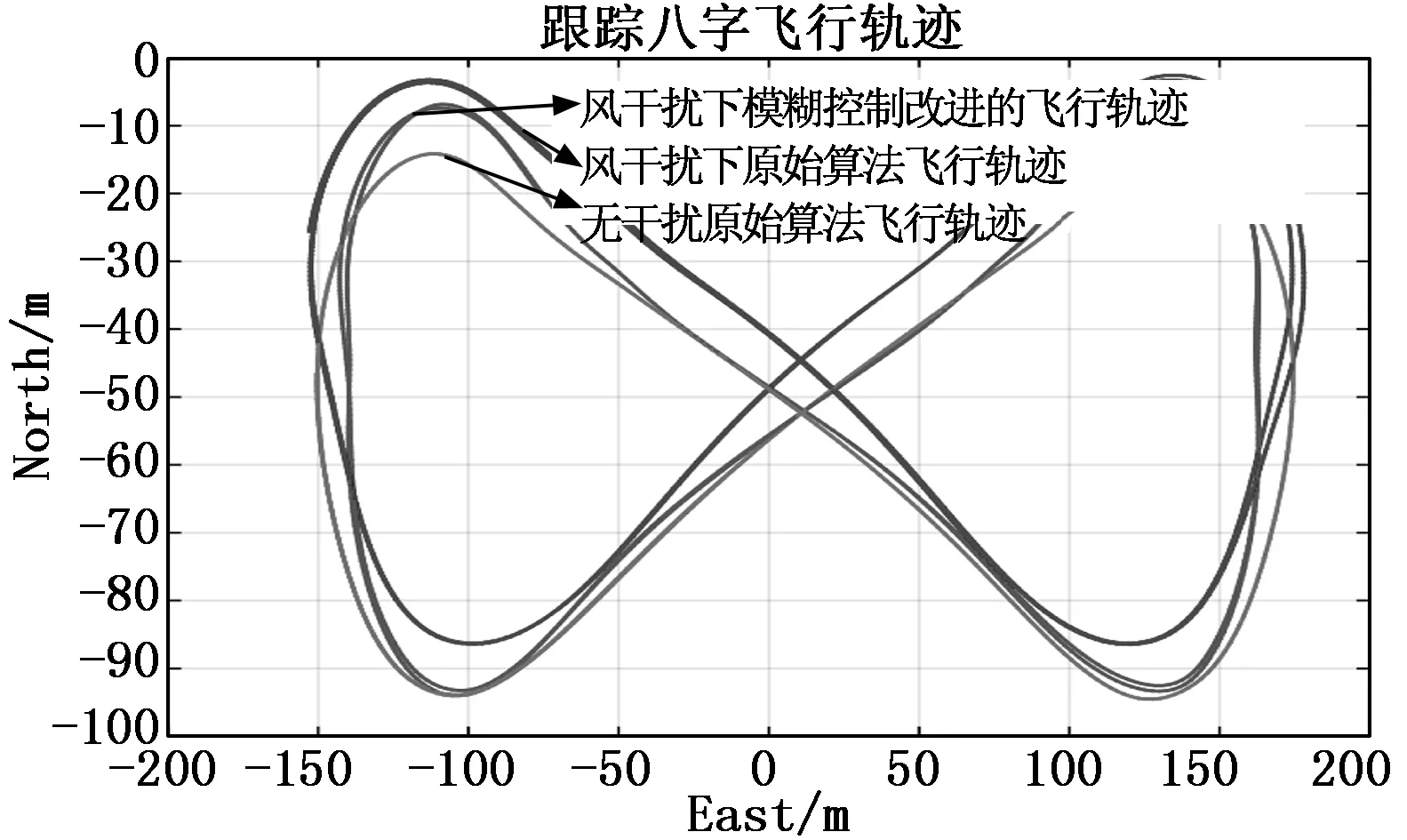
图12 三种情况下飞行轨迹横向平面投影对比

图13 轨迹误差对比
4 结束语
本文基于模糊控制改进的L1-navigation导航算法,在空间八字曲线的导航算法中添加模糊控制,以轨迹误差和轨迹误差变化率为输入量,以计算加速度的增益系数常数为输出,改变加速度的大小,优化轨迹误差。在Ardupilot的SITL仿真飞行结果表明加入模糊控制的导航算法性能优于原始导航算法,提高了空间曲线的跟踪性能,特别是在干扰的情况下(如风),具有很好的自适应性和跟踪性能。本文的方法适用于空间曲线导航控制。
