基于深度自编码网络的智能目标分群算法

陶 宇,蒋序平

(国防科技大学信息通信学院，湖北 武汉 430000)

在信息技术高速发展的现代战争中，通过战场传感器系统搜集到的战场目标信息越来越详尽，即使经过了态势感知系统的初级数据融合，关于战场目标的属性信息仍然较复杂，呈现数据规模大、维度高的特点，这给战场目标数据处理和战场态势生成带来了极大的挑战[1]。

目标分群是战场态势生成的重要任务之一。在战场对抗过程中，双方的兵力通常是按照一定的逻辑序列有规律地聚集在一起，并且，来自不同作战域的战场目标，其所在目标群的内部组成结构也是不同的，根据战场目标之间特殊的关联关系将它们划分到不同群组的过程称为目标分群[2-3]。目标分群的意义在于，将战场空间中传感器平台搜集到的战场目标信息根据其内部的关联关系通过技术手段分成不同类别，每个类别中的战场目标具有一定相似性，这样能够让指挥员对战场态势有一个清晰明了的空间视图。能否高效、智能地实现战场目标分群直接影响了指挥控制的执行效率，也直接决定了指挥员的决策效率[4-5]。

本文研究的智能目标分群算法就是将人工智能中的深度学习技术与传统的目标分群技术相结合，旨在解决对大规模、高维度的战场目标数据的处理难题。该算法能够对来自战场不同空间、不同领域的目标实现智能分群，从而给指挥员提供一个清晰的战场态势关系图，其军事应用前景也十分广阔。

1 自编码网络在目标分群中的应用

自编码网络是指在保持网络输入和输出尽可能一致(通过信息损失来判定)的情况下，通过无监督的训练方式，实现隐层的特征提取和参数学习[6]。自编码网络本身是一种浅层的神经网络，如图1所示是一个对数据降维的基于三层前馈神经网络的自编码结构。其中，输入层和输出层的节点数量是相同的，从输入层到隐层的过程称为数据的分析或编码，从隐层到输出层的过程称为数据的合成或解码。

图1 基于三层前馈神经网络的自编码结构

在自编码网络中，隐层特征的维数决定了自编码网络的功能，当隐层特征的维数大于输入数据的维数，隐层实现的就是对输入数据的稀疏编码功能；当隐层特征的维数小于输入数据的维数，隐层实现的就是对数据的压缩编码功能。本文需解决的问题是对输入的高维数据进行降维，得到其在低维空间上的映射，因此在目标分群模型的设计中，自编码网络的隐层维数需设置为低于输入数据维数[7-8]。

假设一个自编码网络的输入层和输出层的神经元个数均为u，隐层的神经元个数为v，输入数据集为TrainDataSet。

(1)

那么隐层的输出可表示为

X=σa(Wax+ba)

(2)

输出层的输出可表示为

(3)

自编码网络的优化目标函数可以根据能量或者熵的损失准则来构建，本文主要采用基于能量的损失来构建优化目标函数，即

(4)

其中θ为参数项矩阵，μ为正则化系数，R(θ)为正则化函数，即

θ=[Wa,ba;Ws,bs]

(5)

(6)

2 目标分群模型及算法描述

目标分群模型将目标分群的过程分为特征提取阶段和分群精调阶段，模型的具体结构如图2所示。

在特征提取阶段，战场目标数据从模型的输入层进入一个堆栈式自编码网络层，该网络层是由3个自编码器(AE)堆栈构成，经过逐层参数预训练后，将自编码网络层的参数进行初始化，进而得到战场目标数据在低维空间上的特征表示。

图2 基于深度自编码网络的目标分群模型

在分群精调阶段，将战场目标数据的低维特征表示输入目标分群层，当系统给定分群的类别数时，目标分群层输出分群结果，即分群得到的类中心点和各个类之间的距离，再通过ADMM(Alternating Directed Method of Multipliers，ADMM)交替并行地方式优化聚类层以及堆栈式自编码网络层的目标函数，对各层的参数进行精调。ADMM是一种非反向传播的深度神经网络训练方法，该方法通过将目标函数分解为多个子目标的方式来得到全局最优解[9-11]。

2.1 ADMM算法的求解过程

ADMM算法是当前机器学习中使用十分广泛的一种对约束问题优化求解的方法，它是在增广拉格朗日乘子法(Augmented Lagrangians and the Method of Multipliers，ALM)上改进发展而来。

考虑一个凸优化问题如下

minx∈Rnh(x)+o(Dx)

(7)

其中，D是一个列满秩的m×n阶矩阵，h(·)为n维空间的凸型函数，o(·)为m维空间的凸型函数。为方便求解，引入一个虚拟变量z∈Rm，即

minh(x)+o(z)

s.t.z=Dx

(8)

式(8)是一个典型的凸优化问题，对于这一类问题的一般解决方法是采用ALM算法，但该算法的缺点是无法通过分解参数来并行地优化多个参数，而ADMM算法则是很好地克服了这个缺点。ADMM通过引入一个标量参数ρ>0，构造目标函数的增广拉格朗日表达式，即

Lρ(x,z,φ)=h(x)+o(z)+φT(Dx-z)+

(9)

其中,φ为拉格朗日乘子项矩阵。ADMM的迭代步骤为

xk+1∈arg minx∈RnLρ(x,zk,φk)

(10)

zk+1∈arg minz∈RmLρ(xk+1,z,φk)

(11)

φk+1=φk+ρ(Dxk+1-zk+1)

(12)

ADMM通过分解的方式对目标函数中的x和z进行求解，从而使得整个函数在优化过程中是并行且有效的。对于本文提出的深度聚类模型目标函数优化问题，ADMM具有同样的适用性。

由于本文提出的基于深度堆栈自编码网络的目标分群模型是分为两个阶段来构建的，而两个阶段均有各自的目标函数，采用交替迭代优化的方法可以使得整个网络模型的参数收敛，因此基于深度堆栈自编码网络的目标分群模型总体的目标函数为两个训练阶段的加权和，即特征提取阶段的损失函数加上分群精调阶段的类间距离和，即

s.t.Y=fθ1(X)

(13)

根据ADMM算法，其增广拉格朗日表达式可构造如下

(14)

其中，U是一个对偶变量(即λ的倒数)。ρ是一个标量参数，用来控制Y与fθ1(X)之间的距离。通过对参数交替优化的方式，可以对目标函数进行求解，其目标优化流程如图3所示。

Input:输入数据集X,超参数ρ,λ,学习率αOutput:训练完成的深度神经网络,聚类结果1)分别对深度神经网络层的参数θ和聚类层的参数w进行初始化;2)执行如下循环体,直到参数收敛:更新θ:θ=θ-α*dθ更新Y:Y=arg minYλ*Gw(Y)+ρ2‖Y-fθ1(X)+U‖2F更新U:U=U+Y-fθ1(X)更新w:w=arg minwGw(Y)3)返回值θ和w。图3 目标优化流程

2.2 基于深度堆栈自编码网络的k-means目标分群算法

基于深度堆栈自编码网络的k-means目标分群算法(后文简称DAE-k)是将k-means聚类算法嵌入到目标分群模型中的聚类层。该算法的整体思路是首先采用自编码网络对原始数据进行特征提取，得到数据在低维空间上的特征表示之后，再对其采用k-means进行聚类。DAE-k在特征提取阶段的训练目标就是使每一层自编码器输入和输出的损失达到最小，即每一层自编码器所提取到的特征对该层输入数据还原度达到最高；在分群精调阶段，主要训练目标则是通过k-means聚类算法对低维空间的战场目标数据集进行聚类，使每个样本点与其最相近的聚类中心之间的距离最小。因此，DAE-k的目标函数表达形式为

(15)

s.t.yi=fθ1(xi)i=1,2,…,N

(16)

(17)

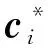
该目标函数的增广拉格朗日表达式为

(18)

为求解上述方程，可以将自编码网络部分看作是一个关于参数θ的非线性非凸函数，然后采用ADMM的方法对目标函数中每个部分的参数变量进行交替优化。具体来说，首先对参数θ采用基于梯度下降的方法求出自编码网络的初始解；对于参数Y，U，C，则根据以下公式进行迭代

(19)

(20)

(21)

其中，Nj表示第j个类簇中样本点的个数，Cj表示由第j个类簇中所有样本点组成的数据集合。

DAE-k算法的流程框图如图4所示。

Input:数据集X,超参数ρ,λ,学习率αOutput:训练完成的深度堆栈自编码网络,聚类结果1)分别对深度堆栈自编码网络的参数θ和聚类层的参数C进行初始化;2)执行如下循环体,直到参数收敛:更新θ:θ=θ-α*dθ更新Y:yi=λ*c*i+ρ*(fθ1(xi)-ui)λ+ρi=1,2,…,N更新U:ui=ui+fθ1(xi)-yii=1,2,…,N更新C:ci=1Nj∑xj∈Cjyij=1,2,…,k3)返回值θ和C。图4 DAE-k算法流程图

2.3 基于深度堆栈自编码网络的GMM目标分群算法

基于深度堆栈自编码网络的GMM聚类算法(后文简称DAE-G)，是在虚拟变量Y之前添加高斯混合，采用交替优化的方式对整个模型各个部分的参数进行优化求解。

由于GMM是通过机器学习得到每个样本点被划分到每一个类中的概率，它的算法过程是首先将K个不同的类别看作是K个不同的高斯分布，然后通过计算得到每个样本点由这K个高斯分布生成的概率，将这些概率值作为每一个高斯分布的权值，加权计算并更新该高斯分布的均值和方差。因此，在这里假设πi为第i个高斯分布的权重系数，zi为K维的二元随机变量，且∑kzik=1，那么就可以定义zik的后验概率为

p(zik=1|yi)=γ(zik)

(22)

设每个类分别服从均值为μk，协方差为∑k的高斯分布。目标分群模型中虚拟变量Y的对数似然函数定义为

(23)

其中，N(yi|μk,Σk)是一个以μk,Σk为参数的多变量高斯分布。于是，DAE-G算法的目标函数可以写为

s.t.yi=fθ1(xi)i=1,2,…,N

(24)

根据ADMM优化方法，其增广拉格朗日表达式为

(25)

那么，yi的更新公式为

(26)

其中，I是一个单位矩阵。参数U,μ,Σ,π则服从标准GMM算法的更新方式，即

(27)

(28)

(29)

(30)

由此可以列出DAE-G算法的流程框图如图5所示。

Input:数据集X,超参数ρ,λ,学习率αOutput:训练完成的深度堆栈自编码网络,聚类结果1)分别对深度堆栈自编码网络的参数θ和GMM的参数μ,Σ,π进行初始化;2)执行如下循环体,直到参数收敛:更新θ:θ=θ-α*dθ更新Y:yi=λ∑Kk=1γ(zik)Σ-1k+ρI -1[ρ*(fθ1(xi)-ui)+λ∑Kk=1γ(zik)Σ-1kμk)] i=1,2,…,N更新U:ui=ui+yi-fθ1(xi) i=1,2,…,N更新μ:μk=1Nk∑Ni=1γ(zik)yi k=1,2,…,K更新Σ:Σk=1Nk∑Kk=1γ(zik)(yi-μk)(yi-μk)T k=1,2,…,K更新π:πk=NkN k=1,2,…,K3)返回值θ,μ,Σ,π。图5 DAE-G算法流程

3 实验仿真分析

3.1 实验数据集来源

本文得到的原始战场目标数据集共有5个(均来源于UCI公开数据集)，将其编号为D01，D02，D03，D04，D05，如表1所示。数据集中包括水面、水下、陆地、空中多个空间的目标，并且目标维度最小的数据集有25维，最多的数据集有250维，满足了原始战场目标数据集应当具有的多维性和多样性特点。此处的属性维度是指来自多个传感器平台对某一战场目标的属性状态的描述。

表1 原始战场目标数据集

3.2 实验实施

3.2.1 评价标准

为避免使用单一评价方法的局限性，并且让实验结果更有说服力，本文采用了3种评价方法对目标分群算法的最终聚类效果进行评价，分别为Purity、ACC、NMI[12-13]。

Purity的评价公式为

(31)

ACC的评价公式为

(32)

其中，map(ri)为聚类结果的标签，li为原始数据的真实标签，N为样本点总数。

NMI的评价公式为

(33)

3.2.2 实验内容

为了验证本文提出的基于深度学习技术的目标分群模型和DAE-k、DAE-G两种聚类算法在战场目标数据集上的有效性，本文所进行的实验内容主要有：

1)采用传统的标准k-means聚类算法和GMM算法分别对每个战场目标数据集进行聚类，并运行10次，将这10次聚类结果的平均值作为最终标准k-means聚类算法和GMM聚类算法的聚类结果；

2)采用本文提出的DAE-k聚类算法分别对每个战场目标数据集进行聚类，设置超参数λ=1，并采用线性搜索的方式寻找最佳的ρ值，设置学习率α=0.05，设置最大迭代次数为200；

3)采用本文提出的DAE-G聚类算法分别对每个战场目标数据集进行聚类，设置超参数λ=1，并采用线性搜索的方式寻找最佳的ρ值，设置学习率α=0.05，设置最大迭代次数为200。

3.2.3 实验结果与分析

根据实验实施方案中设定的参数值，本文将传统的标准k-means、GMM聚类算法以及本文提出的基于深度学习技术的DAE-k、DAE-G聚类算法，对每个经过预处理的战场目标数据集进行聚类，其详细分群结果如表2,图6a)b)c)d)e)所示。其中，图6a)为四种分群算法在数据集D01的分群结果；图6b)为四种分群算法在数据集D02的分群结果；图6c)为四种分群算法在数据集D03的分群结果；图6d)为四种分群算法在数据集D04的分群结果；图6e)为四种分群算法在数据集D05的分群结果。

表2 四种聚类算法的聚类结果

图6 k-means、GMM、DAE-k、DAE-G在各数据集上的分群结果

从表2和图2中的聚类准确度可以看出，在本文构建的5个数据集上，DAE-k的聚类效果要优于k-means，DAE-G的聚类效果要优于GMM。从4种聚类算法整体来看，在数据集D01、D02、D03、D05中基于深度学习技术的DAE-k与DAE-G聚类算法相比于传统的标准k-means、GMM聚类算法在聚类效果上均有一定优势。而在数据集D04中，DAE-G的聚类效果与k-means、GMM的水平相当。

由于数据集D01、D02、D03、D05相比于D04的目标属性维度较高，因此根据上述图表对四种聚类算法的聚类效果分析，可以认为本文提出的基于深度学习技术的DAE-k、DAE-G聚类算法在解决高维、大规模数据集的聚类问题上，具有很好的适用性和有效性，且相较于传统的标准k-means、GMM聚类算法在聚类准确度上有明显的提高。而数据集D04为目标属性维度较低的数据集，在对这类数据集进行聚类时，DAE-k、DAE-G聚类算法的优势相比于k-means、GMM聚类算法的优势就不再明显了，这是因为DAE-k、DAE-G聚类算法在深度堆栈自编码网络中的特征提取阶段，将低维数据的特征空间进行了降维后，使得原始数据的特征结构发生了变化，而k-means、GMM聚类算法则是在原始数据特征上进行聚类，而数据本身维数较低，因此聚类效果较好。

4 结束语

综合以上实验结果，可以得出以下几个结论：

1)对于来自不同空间作战域的大规模、高维战场目标数据集的分群问题，本文提出的DAE-k和DAE-G两种目标分群算法是有效的；

2)DAE-k和DAE-G两种目标分群算法在处理大规模、高维战场目标数据集时，分群的效率明显高于传统的k-means和GMM聚类算法；

3)对于不同规模、不同维度的战场目标数据集，DAE-k和DAE-G两种目标分群算法的适用性不同；

4)提出的基于深度堆栈自编码网络的目标分群模型可应用于实际战场目标分群问题的研究中。

本文通过研究深度学习和聚类技术的原理，构建出基于深度堆栈自编码网络的目标分群模型，该模型结合了深度学习的降维特点以及聚类技术的高效分类优点，进而设计了DAE-k和DAE-G两种目标分群算法，实验的结果表明，相比于传统的目标分群方法，本文提出的基于深度堆栈自编码网络的目标分群模型及算法，在解决大规模高维数据的降维分类问题上具有很大优势，但仍然存在一些不足且需要继续深入研究的地方，主要体现在基于深度学习的目标分群模型由于需要训练的参数量级大，导致计算复杂度上升，为了节省物理内存，提高计算效率，下一步的研究工作是力图将基于深度学习的目标分群模型结构进行简化和改进。