四旋翼飞行器串级模糊自适应PID优化控制系统研究
2020-12-07盛广润高国伟李璇烨罗丹
盛广润 高国伟 李璇烨 罗丹


摘 要: 四旋翼飞行器控制系统具有非线性、耦合性等特性,PID参数的整定会存在一定的难度,而且固定的参数无法适用于四旋翼面临的复杂环境。要实现四旋翼的优化控制需要进行自适应性改进。该文结合PID控制和模糊控制的优点,设计一种非线性化的串级模糊自适应PID控制系统,分别在外环角度、内环角速度控制器中加入模糊自适应PID控制器,增强系统的自适应性和准确性。并且针对四旋翼存在高频干扰的特性,提出在角速度模糊自适应PID控制器的微分环节后加入一阶惯性环节,不完全微分提高了微分控制抗干扰能力。通过Matlab仿真实验对比结果表明,所设计方法响应速度快、超调量小,且增强了四旋翼控制的自适应能力和鲁棒性。
关键词: 四旋翼飞行器; 优化控制; 自适应PID控制器; 微分控制; 仿真实验; 结果分析
中图分类号: TN876?34; TP273 文献标识码: A 文章编号: 1004?373X(2020)22?0067?05
Abstract: The control system of four?rotor aircraft has the characteristics of nonlinearity and coupling, The PID parameters setting will be difficult to some extent, and the fixed parameters cannot be applied to the complex environment faced by the four?rotor. The adaptive improvement is needed to realize the optimal control of four?rotor. A nonlinearized cascade fuzzy self?adaptive PID control system is designed in combination with the advantages of PID control and fuzzy control, from which the fuzzy self?adaptive controller is added to the outer loop angle controller and the inner loop angular velocity controller respectively to enhance the adaptability and accuracy of the system. In allusion to the high?frequency interference characteristics of the four?rotor, a first?order inertia link is added after the differential link of the angular velocity fuzzy adaptive PID controller. The incomplete differential improves the anti?interference ability of the differential control. The simulation comparison and experimental verification on Matlab are performed. The results show that the designed method has fast response speed and low overshoot, which significantly enhances the self?adaptive ability and robustness of four?rotor control.
Keywords: four?rotor aircraft; optimal control; self?adaptive PID controller; differential control; simulation experiment; results analysis
0 引 言
近几年MEMS技术的快速发展,集成电路芯片化、模块化都为小型飞行器提供了丰富的技术条件。市场上众多种类的飞行器中,四旋翼尤其受到青睐。因为其集合了不同飞行器的优点,结构简单,只需要转动4个对称电机就能够消除空气扭矩、陀螺效应的影响,使用方便,成本低。在军事探查、智慧物流、影视航拍等领域得到了广泛的应用,具有极高的研究意义。控制系统研究是四旋翼飞行器研究的关键部分,也是国内外研究的热点。四旋翼无人机是一个欠驱动、非线性、多变量、强耦合的复杂系统[1]。文献[2]提出的传统PID控制适用于线性系统类型的工程应用,其控制参数固定不变,很难适应四旋翼的灵活性。文献[3]采用双闭环串级控制。外环是角度PID控制,内环是角速度PID控制,能够减小角度PID控制对参数调节的敏感性。文献[4]提出模糊控制,可以解决PID控制在非线性控制中抗干扰能力差的问题,模糊控制作为一种先进控制策略可以在非线性系统中取得较好的控制效果。针对以上的问题,本文提出的控制算法将模糊控制和串级PID控制融合。串级模糊自适应PID优化控制不依赖精确的数学模型,还可以实现模糊控制中PID量化因子的自整定。在此基础上,针对在四旋翼飞行器控制系统中微分项对高频干扰的敏感性易导致输出震荡,在角速度PID控制器的微分环节增加了一阶惯性环节,对微分信号进行滤波,消除高频干扰,降低微分环节对系统的影响。
1 四旋翼飞行器数学建模
1.1 坐标建立
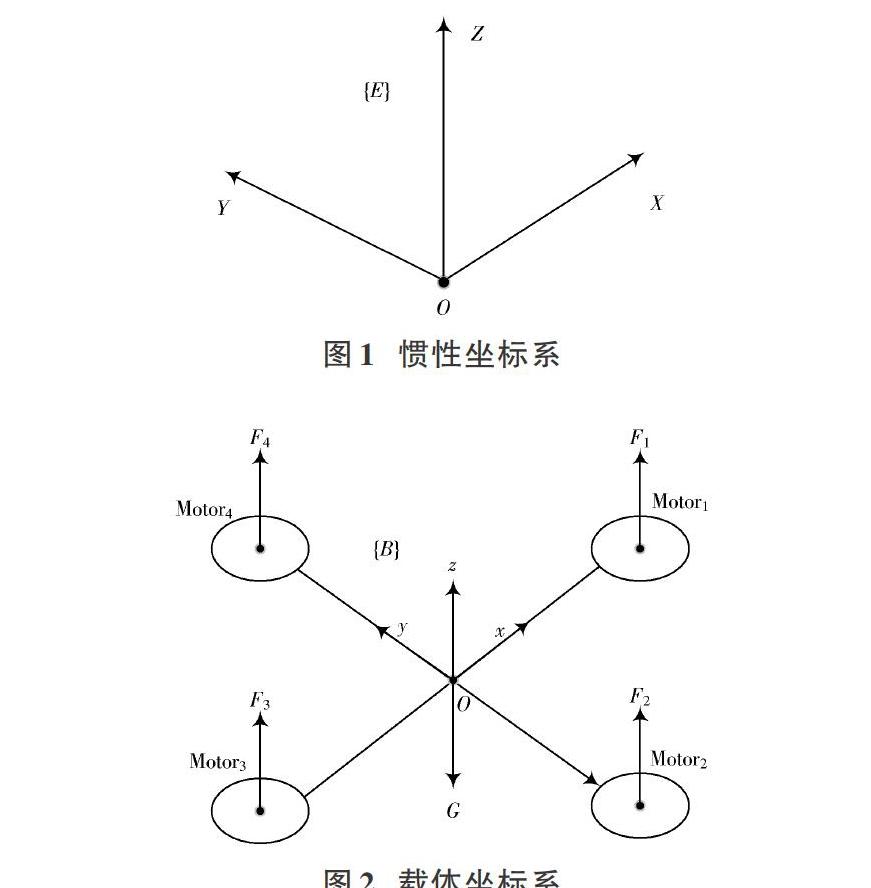
首先,在获得无人机的数学模型之前,需要建立2个坐标系:惯性坐标系E(O?XYZ)和载体坐标系B(O?xyz)如图1和图2所示。
1.2 飞行原理
如图2所示,四旋翼飞行器的动力来自于电机M1~M4产生的不同转速,相邻的电机转向相反。所谓四旋翼具有六自由度物理运动状态,即:上下、前后、左右、横滚、俯仰、偏航运动。当4个电机转速一样,同时增加或减少,飞行器做垂直起降;当M2和M4转速保持不变,增大(减小)M3转速,飞行器绕y轴旋转产生俯仰角,并向前(后)运动;当M1和M3转速保持不变,增大(减少)M2转速,绕x轴旋转产生横滚角,并向左(右)运动;当M1,M3转速和M2,M4转速不相等,绕z轴旋转产生偏航角且运动。
1.3 数学建模
建立模型的过程中,为了不失常规性,需要做以下假设[6]:
1) 四旋翼飞行器为刚体,均匀对称。
2) 机体所受阻力和重力不因飞行高度变化产生影响。
3) 飞行器各方向拉力和桨叶转速成正比例。
假设z轴向上为正,飞行器不产生反向转矩,并且与电机、升力保持垂直,M为所受力矩之和,m为飞行器质量,[Fx],[Fy],[Fz]为F在载体坐标系3个轴的分量,G为重力,根据牛顿第二定律:
2 串级模糊PID控制器设计
2.1 串级模糊自适应PID控制器结构
模糊自适应PID控制器主要是由PID控制器和模糊控制器组成[8]。模糊PID控制器的输入量为偏差e和偏差变化率ec。其中,模糊控制器分为模糊化、模糊推理、去模糊化(清晰化)[9]。输出为PID参数变化量:[ΔKP],[ΔKI],[ΔKD],完成实时调节PID控制器。
四旋翼飞行器作为被控对象,单级角度控制易出现震荡情况,为了抑制并对角速度进行更好的控制,本文提出了串级模糊自适应PID控制算法:外环为角度模糊PID控制器,作用是控制飞行器角度;内环为角速度模糊PID控制器,用于控制四旋翼飞行器的角速度。控制结构图如图3所示。
2.2 角速度模糊PID控制器优化
在PID控制器中,微分环节的引入虽然可以加快系统调节时间,但是对于飞行器存在的高频干扰特性会较为敏感,这就是微分项在误差扰动时的缺点。
为了克服这个不足,采用在角速度模糊自适应PID控制器中引入一个一阶惯性环节[11+Tfs],可以对微分信号进行平滑处理,消除高频噪声信号,形成基于不完全微分的模糊自适应PID控制器。不完全微分PID結构图如图4所示。
2.3 系统隶属度函数建立
角度、角速度控制部分均为双输入、三输出系统。输入为角度、角速度的偏差e和偏差变化率ec,定义模糊子集为{NB,NM,NS,ZO,PS,PM,PB}[11],e和ec的论域范围为{-6,6}。输出为角度控制环的[ΔKP],[ΔKI],[ΔKD],以及角速度控制环的[ΔKP(1)],[ΔKI(1)],[ΔKD(1)]。[ΔKP(1)]论域范围为{-3,3},[ΔKI(1)],[ΔKD(1)]论域范围{-0.6,0.6}。输入变量隶属度曲线见图5,输出变量隶属度曲线如图6、图7所示。
2.4 系统模糊规则建立
建立合理的模糊规则对于模糊自适应PID控制器来说十分关键。从系统的稳定性、超调量、响应速度进行综合衡量。总结实际调试操作经验和理论知识对KP,KI,KD的作用进行分析,如果e和ec越大,KP应该越小,避免误差变化幅度过大;KI作用是减小稳态误差,应该变大;KD可以减小超调量。模糊控制规则见表1~表3。
3 仿真与分析
3.1 仿真实验
根据四旋翼飞行器的数学模型及串级模糊自适应PID控制结构框图,在Matlab仿真平台进行脚本编辑,其中,常微分函数的求解采用Matlab中的ode45(Runge?Kutta)算法[12]。将输入/输出隶属度函数和模糊规则进行函数编辑。模糊集合合成与运算采用最小隶属法(MIN Implication)或最大隶属法(MAX Implication),去模糊化(清晰化)规则采用重心法[13]。
为了对比不同系统的控制效果差异性,将单级、串级PID、串级模糊自适应PID同时进行仿真实验。首先是动态仿真,给定滚转角、俯仰角、偏航角目标角度,分别为[5°,5°,1°],初始角度均设定为0°,观察变化曲线。为了测试四旋翼飞行器采用不同控制算法下的抗干扰性能,在飞行器仿真完成动态实验对比后,t=2 s时加入阶跃干扰信号。观察恢复稳定的控制效果[15]。对比仿真如图8~图10所示。
3.2 结果分析
从图8~图10中可以看出,飞行器在接收到滚转角、俯仰角、横滚角的给定目标后,立即开始动作,单级PID控制下,飞行器达到稳定姿态的响应时间约为1.7 s;串级PID控制下,响应时间为1.5 s;而串级模糊自适应PID控制下,达到稳定状态的响应时间缩小到0.7 s左右,比单级、串级PID控制稳定时间分别提高了58.8%和53.3%。说明了串级模糊自适应PID控制算法提高了系统的快速性。当到达各个给定目标角度后,以图8滚转角为例,单级PID控制下产生6%的超调量,串级PID控制下超调量为5%,相比之下,串级模糊自适应PID控制没有超调,说明提高了系统的稳定性。
从图8~图10中可以看到,当飞行器姿态达到稳定状态后,t=2 s开始加入阶跃脉冲信号。以图9俯仰角为例,串级模糊自适应PID控制算法从被干扰到恢复稳定状态响应时间为0.6 s,串级PID控制、单级PID控制分别为0.8 s和1.3 s。
4 结 论
本文针对四旋翼飞行器的非线性特性,提出将模糊控制理论结合串级PID控制系统,融合了二者的优点,并且在角速度模糊自适应PID控制部分的微分环节后加入了一阶惯性环节,对控制系统进行了进一步优化。通过对该文系统与单级PID、串级PID的仿真实验对比发现,串级模糊PID控制可以实现四旋翼飞行器对PID参数的自适應整定;相对于单级、串级PID控制,快速性方面提高了58.8%,53.3%,也增加了稳定性;加入干扰环节,结果证明,抗干扰性能明显更加优越。综上,本文提出的串级模糊自适应PID优化控制系统能很好地满足四旋翼飞行器的姿态控制需求。
注:本文通讯作者为高国伟。
参考文献
[1] 付雷.基于MEMS的四旋翼飞行器姿态估计与控制系统研究[D].武汉:武汉科技大学,2019.
[2] LI Y W, WANG H F. Fuzzy adaptive PID control for six rotor eppo UAV [J]. Journal of Hebei University of Science & Technology, 2017(1): 14?21.
[3] 贾峰,孙曼,秦磊.基于STM32的四旋翼飞行姿态串级控制[J].科学技术与工程,2015,15(6):220?225.
[4] 张萍,雷宁.基于模糊PID四旋翼飞行器姿态控制[J].航空计算技术,2019,49(3):115?118.
[5] 秦永元.惯性导航[M].2版.北京:科学出版社,2014.
[6] 唐堂,罗晓曙.四旋翼无人机姿态非线性控制研究[J].计算机仿真,2019,36(1):71?75.
[7] 陈听雨.四旋翼飞行器建模、仿真与PID控制[J].电子世界,2018(21):5?7.
[8] 何立璐,易映萍,石伟.基于自适应模糊PID运动控制系统的设计[J].软件,2019,40(6):7?12.
[9] 张建学.基于四旋翼无人机模糊PID控制系统研究[J].电子测试,2019(7):24?25.
[10] 李林升,丁鹏,钟成.不完全微分与微分先行的农业机器人巡航PID控制算法[J].机械设计与研究,2018,34(1):45?49.
[11] CHEN Siyu, CHEN Wei. Design of power cable UAV intelligent patrol system based on adaptive Kalman filter fuzzy PID control [J]. MATEC web of conferences, 2017(2): 100.
[12] LIU Guiqiao, SUN Ying, LI Longfa, et al. Trajectory tracking of 4?DOF assembly robot based on quantification factor and proportionality factor self?tuning fuzzy PID control [J]. International journal of wireless and mobile computing, 2020, 18(4): 361.
[13] 陈侠,梁红利,尹立远.基于FHM的四旋翼飞行器悬停控制方法[J].计算机仿真,2019,36(9):38?46.
[14] 夏国清,陈华珍.模糊理论和PID相融合的两轮自平衡机器人智能控制系统[J].现代电子技术,2018,41(21):117?120.
[15] 张小明,于纪言,王坤坤.自抗扰PID四旋翼飞行器控制方法研究[J].电子技术应用,2019,45(3):84?87.