基于最大利润模型的高速公路充换电站选址

贾林国 周小琳 姚博彬 叶珍 武奇生

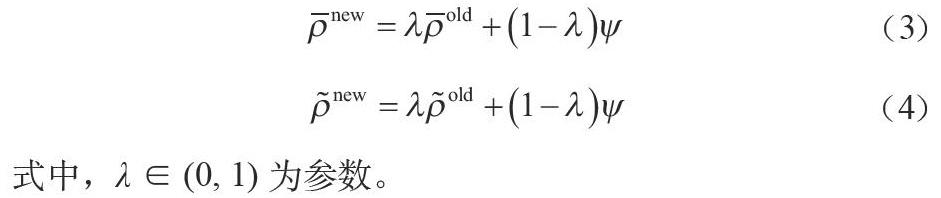
摘 要：合理有效的高速公路充换电站选址布局是提升路网效率的关键。为了满足电动汽车用户的通行需求并兼顾投资建设的利润回报，文中设计了用于电动汽车充换电站选址规划的最大利润模型，同时也提出了一种基于自适应大邻域搜索的算法对上述模型进行启发式求解。算例对比实验表明，文中所提算法的优化性能明显优于采用遗传算法得到的结果，证明了文中所设计的最大利润模型的有效性。

关键词：高速公路;电动汽车;充换电站选址;最大利润模型;自适应大邻域搜索算法;遗传算法

中图分类号：TP391文献标识码：A文章编号：2095-1302（2020）11-00-03

0 引 言

电动汽车作为一种新能源汽车，与传统燃料汽车相比具有节能、环保等优点，正逐渐发展成为当前社会的主力交通工具。相比传统燃料汽车，电动汽车的续航是制约其在高速公路场景下行驶的短板。为了弥补短板，国家“新型基础设施建设”中特将充换电站作为重点建设目标之一。然而，由于受到政策、资金和空间区域规模等因素的限制，在高速公路沿线的每个服务区或停车区建设充换电站是不现实的。因此需要进行电动汽车充换电站的选址规划研究。目前，针对电动汽车充换电站选址模型的研究，从点需求来看，主要是根据基于P-中位和P-中心的最大覆盖模型;而考虑流量需求，则主要是根据基于流量补给选址模型来考虑最小建站成本和库存成本[1-7]。

与上述研究不同，本文同时考虑了满足用户出行服务需求和充换电站运营利润回报两个因素，设计了基于最大利润模型的充换电站选址模型及其有效求解算法。

1 充换电站选址问题

目前充换电站选址模型大多是在基于路径已知的情况下最小化总成本（包括建设成本和电能库存成本），但并没有考虑盈亏情况。

假设路网中共有N个节点，构成点集N。定义变量hi=1，表示在节点i处建立充换电站;否则，hi=0。令fhi表示在节点i∈N建立充换电站后的总交通流量，它是由经过该节点的不同路径q∈Q的交通流量fqhi叠加得到。路网的最大利润与电动汽车一次充换电所需费用ei、电能库存单位成本si和充换电站建造成本ci有关，即最大利润模型要求寻找某一子集∩N使得公式（1）所示的代价函数J最大化。

式中，Q为所有路径的集合。在约束条件中，二值化的决策变量hi和路径流量fhi是代价函数中的两个重要参数。

从公式（1）中可知，求解该模型的核心是必须得到每个候选建站节点的交通流量;而交通流量又会根据是否在该节点建站而发生变化，即每个充换电站的流量与电动汽车所选择的路径有关。为了解决如上问题，可以对路网中所有出发地-目的地对（OD对）先考虑做不带剩余电量的最短路径规划，然后在选址时令选址点必须满足所有OD对路径上电动汽车的充电需求。有了固定的路径以及选址组合，就可以计算选址点中的交通流量。但是电动车用户在最短路径上并不需要在每个充换电站点补给电能。这就意味着，在计算流量时，还需要考虑电动汽车的充换电决策，即在哪个充换电站进行能源补充。

2 基于自适应大邻域搜索的求解方法

可以用Dijkstra算法[8]确定最短路径;对于充换电站策略选择，由于单一路径上的充换电站节点数量有限，可以用穷举法求解。但对最大利润模型的求解却是十分困难的，因为随着节点规模的增大，选址方案呈指数级增长，属于NP-hard问题。因此，模型求解的关键就在于如何设计有效的近似算法。在数学优化中，特别是针对组合优化问题，邻域搜索是在当前解的邻域范围内重复将该解转变为其他解并最终获得近似最优解的有效手段之一。当邻域规模無法显式定义时，可采用一个破坏（Destroy）方法破坏解并用修补（Repair）方法修复解来隐式地定义邻域。自适应大邻域搜索（Adaptive Large Neighborhood Search，ALNS）算法采用了多种Destroy方法和Repair方法，并在迭代过程中为Destroy方法和Repair方法动态分配权重[9]。算法流程见表1所列。

在表1中，和Ω分别表示Destroy方法和Repair方法的集合，而和表示各自的权重。

每次搜索之后，将采用如下函数为每个Destroy方法和Repair方法进行评估：令ψ∈{ω1， ω2， ω3， ω4}，其中ω1>ω2>ω3>ω4>0为自定参数，分别表示“新解是当前全局最优解”“新解比当前解更好”“新解被接受”“新解被拒绝”四种情况下的权重。Destroy和Repair方法的权重更新规则为：

式中，λ∈（0， 1）为参数。

在求解最大利润模型时，本文所设计的Destroy方法是在可行解O中n个充换电站节点进行破坏。破坏策略有三种：

（1）不考虑流量，随机取出n个站点进行破坏;

（2）选择n1个流量较大的站点和n2个流量较小的站点进行破坏，n1+n2=n;

（3）通过计算每个站点的流量，选择流量较小的n个节点进行破坏。为了保证解的稳定，本文中规定破坏的点数满足n≤|O|/4。

本文所设计的Repair方法有两种：

（1）随机添加节点直到解满足约束条件;

（2）利用被破坏后的解对所有OD对做满足可达性检验，找出所有潜在节点中流量最大的节点。

经过Destroy和Repair操作后，需要决定是否接受新解。本求解方法所采用的准则包括Metropolis接受准则[10]和Random Walk接受准则[11]（以下简称M接受准则和R接受准则）。前者是当新解比原解差时以概率P=exp{α[J（Onew）-J（Oold）]}接受新解，参数α在初始时设为较小的数（使接受新解的概率较大），随着迭代进行，逐渐变大（使接受新解的概率降低，变稳定）;后者则是不管新解是好是坏全都接受。为了方便，将前者称为ALNS-M算法，后者称为ALNS-R算法。

3 算例设计与数值结果分析

算例中使用的交通网络节点分布如图1所示，共有30个节点。考虑到部分OD对路径较短的情况，筛选出了296个主要的OD对，并用Dijstra算法求出了每个OD对的最短路径;每个OD对的流量通过重力模型计算：fq=（wiwj/dij）×1.5，其中wi和wj分别表示OD对起点和终点的权重。在本算例中权重由计算机在区间[300，600]之间随机生成。

自适应大邻域搜索算法中各Destroy和Repair方法的初始权重都设为1;四种权重更新情况所对应的权重值分别设定为3，2，1，0.5。为了便于性能比较，使用遗传算法[12]（Genetic Algorithm，GA）求解，参数设置如下：交叉概率为0.7、变异概率为0.6、种群规模为50、迭代次数为200。三种算法的初始解可以由计算机随机生成。图2和图3分别给出了自适应大邻域算法在M接受准则和R接受准则下每次迭代的代价函数值。

在表2中，本算例给出了遗传算法以及ALNS算法在两种接受准则下的最佳选址方案及所获得的利润。

从上述结果来看，两种不同接受准则下的自适应大邻域搜索算法的性能都要优于遗传算法，而且M准则比R准则更好。主要原因是本算例所设计的基于最大利润模型的充换电站选址具有一定的随机性，这就使得遗传算法没有一个明确的进化方向，所以导致算法不能有效地寻优。而对于自适应大邻域搜索算法，基于流量最小的Destroy方法和基于流量最大的Repair方法的使用和接受的次数要远多于其他方法，可见基于流量的修补和破坏策略更有助于良好解的产生;而对于M准则和R准则而言，前者的优化结果要比后者更好，这就证明了自适应大邻域搜索可以根据当前较优解产生更优解。

4 结 语

本文针对高速公路充换电站选址规划问题提出了更具实际意义的最大利润模型。该模型包含两个基本问题，即最短路径问题和电能补给决策优化问题。结合模型特点，本文设计了基于自适应大邻域搜索算法对模型进行启发式求解。通过算例验证，表明自适应大邻域搜索算法明显优于遗传算法。

参考文献

[1] HAKIMI SL. Optimum locations of switching centers and the absolute centers and medians of a graph [J]. Oper Res，1964，12（3）：450-459.

[2] Constantine Toregas，Charles ReVelle. Optimal location under time or distance constraints [J]. Papers of the Regional Science Association，1972，28（1）：131-143.

[3] Richard Church，Charles ReVelle. The maximal covering location problem [J]. Papers of the Regional Science Association，1974，32（1）：101-118.

[4] M John Hodgson. A Flow-Capturing Location-Allocation Model [J]. Geographical analysis，1990，22（3）：270-279.

[5] Inês Frade，Anabela Ribeiro，Gon?alo Gon?alves，et al. Optimal location of charging stations for electric vehicles in a neighborhood in lisbon portugal [J]. Transp Res Rec，2011（1）：91-98.

[6] Baouche，Fouad，Billot，et al. Efficient Allocation of Electric Vehicles Charging Stations：Optimization Model and Application to a Dense Urban Network [J]. IEEE intelligent transportation systems magazine，2017，6（3）：33-43.

[7] Sung Hoon Chung，Changhyun Kwon. Multi-period planning for electric car charging station locations：a case of korean expressways [J]. Eur J Oper Res，2015，242（2）：677-687.

[8]陸锋，卢冬梅，崔伟宏. 基于四叉堆优先级队列及逆邻接表的改进型Dijkstra算法[J]. 中国图象图形学报，1999，4（12）：3-5.

[9]胡大伟，陈希琼，高扬. 定位-路径问题综述[J]. 交通运输工程学报，2018，18（1）：111-129.

[10]庞峰.模拟退火算法的原理及算法在优化问题上的应用[D].长春：吉林大学，2006.

[11] WANG F，LANDAU DP. Efficient，multiple-range random walk algorithm to calculate the density of states [J]. Phys Rev Lett，2001，86（10）：2050-2053.

[12]高媛. 非支配排序遗传算法（NSGA）的研究与应用[D]. 杭州：浙江大学，2006.