区域交通微循环支线网络交叉口无冲突交通流组织优化*
2020-12-07陈群刘嘉晖
陈群, 刘嘉晖
(中南大学 交通运输工程学院, 湖南 长沙 410075)
道路交通网络包含城市交通网络与公路交通网络。公路交通网络一般相互交叉的道路较少,高等级公路交叉采用互通或不互通的立交设计,低等级公路相交通常采用信号控制交叉口(流量较大时)或无信号控制交叉口(流量较小时)。相比于公路交通网络,城市交通网络中各种干道、次干道、支路相互交叉,交通复杂,大、小交叉口众多,互相冲突的交通流在交叉口通过信号灯作时间上的分离(对于交通量小的次要交叉口作优先控制或无控制),车辆在交叉口由于等待而浪费大量时间。据估计,车辆通过交叉口的时间占整个通行时间(交叉口、路段通行总时间)的30%~40%,而且交叉口通常是行车事故多发地。
为减少车流在交叉口的冲突,通常采用路段单向行驶和交叉口禁左、禁直等交通流组织方式,使车辆通过迂回的方式避免在交叉口上互相冲突。但这些交通组织方式有适用范围,在干道上实施可能引起车流过大的迂回,而且有时并不具备单行、禁行的交通组织条件。相对来说,如果是在城市局部的某个区域内,该区域互相平行或垂直交叉的微循环道路较多,车辆可选择的路径较多,组织某些线路单行、某些交叉口禁直或禁左则有利于整个车辆的流通,减少车流在交叉口的冲突与延误。该文针对某个区域路网的交通组织优化,通过路段单行和交叉口进口道上禁直、禁左等交通组织方式的选择优化,使总的车流运行效率最大。
1 优化模型
一定区域内路网由许多路段及路段相交的交叉口组成,若每个交叉口上各进口道车流无交通管理措施,会有直行、右转、左转3种选择。在交叉口,右转车流一般不会与其他车流相冲突,主要是各进口道的直行、左转车流互相冲突和干扰而产生干扰延误。因此,如果对交叉口各进口道上车流实施禁直或禁左优化,可使任意两股车流在交叉口上都无冲突,并按优化后的线路行驶。同理,在路段上同时实施单向行驶或双向行驶,进行一体化优化。
将整个区域网络上路段与交叉口整体考虑,则各交叉口各进口道是否实施禁直或禁左、支路路段上实施单向或双向行驶为决策变量,整个网络车流运行效率可通过各车流OD在网络上的总运行时间来衡量,考虑的约束为交叉口上任意两股车流都无冲突(这样即可不用考虑对两股相冲突的车流进行时间上的隔离,可减少延误和冲突)。因此,优化问题的目标为总的OD车流行驶时间最小,并满足任意交叉口上任意两股方向的车流都无冲突。
图1为区域路网示意图。对于给定的区域道路网络(V,A(y)∪B(z)),其中V为节点集,记n=|V|,A(y)为交叉口上直行与左转连接边集合,B(z)为路段集合。y、z为决策变量组成的向量,其中“1”表示该路段(或交叉口连接边)被选择,“0”表示不选。
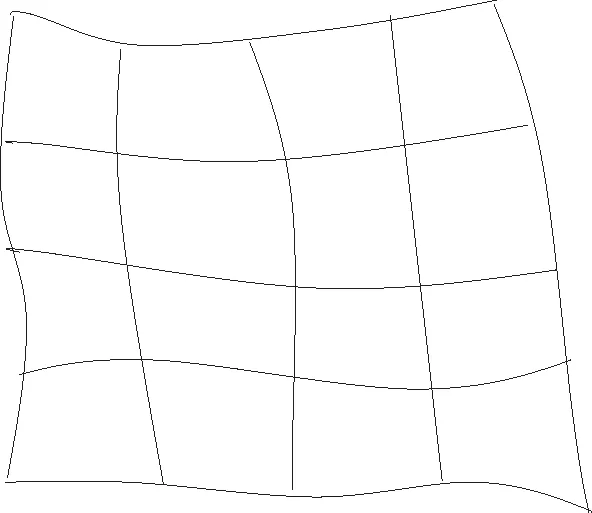
图1 区域路网示意图
十字形交叉口车流冲突情况见图2、图3,T形交叉口车流冲突情况见图4~6。
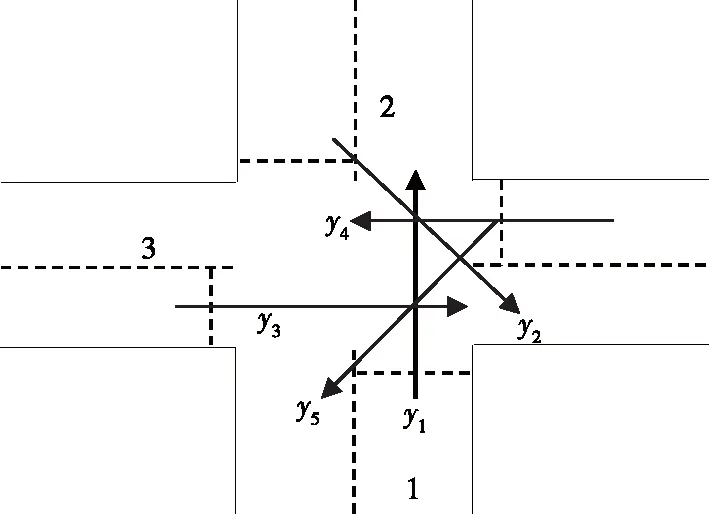
图2 十字形交叉口上与某进口道直行相冲突的车流分析
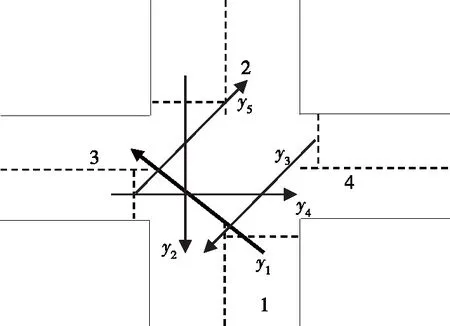
图3 十字形交叉口上与某进口道左转相冲突的车流分析
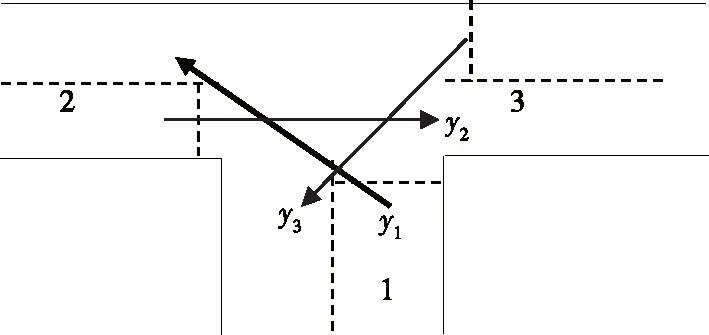
图4 T形交叉口上与侧边进口道左转相冲突的车流分析

图5 T形交叉口上与主边进口道直行相冲突的车流分析
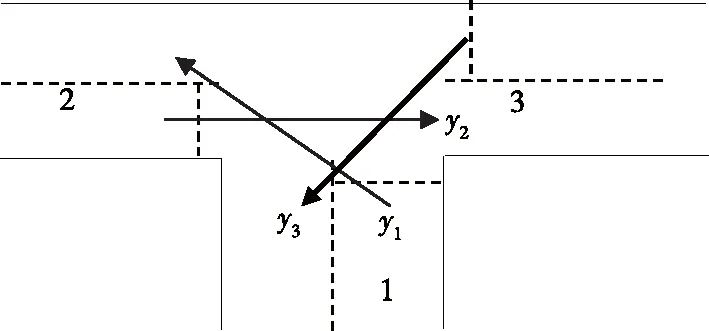
图6 T形交叉口上与主边进口道左转相冲突的车流分析
根据图2,如果y1=1,那么y2=0,y3=0,y4=0,y5=0。根据图3,如果y1=1,那么y2=0,y3=0,y4=0,y5=0。根据图4,如果y1=1,那么y2=0,y3=0。根据图5,如果y2=1,那么y1=0,y3=0。根据图6,如果y3=1,那么y1=0,y2=0。
基于图4~6的分析,若T形交叉口满足y1+y2+y3≤1,可避免在T形交叉口上的车流冲突。
对于区域内支路路段(B(z)),2个节点之间包含相反方向的2条路段,当某个方向的路段对应的决策变量为1时表示该方向的路段被选择,否则不被选择;如果2个方向的路段对应的决策变量都为1,则2个节点之间车流双向行驶。一般来说,如果实施单向通行,由于消除了对向车流的干扰,其通行能力大于双向行驶时2个方向总的通行能力。
对于交叉口连接边(A(y)),如果ya=1,a∈A,则表示连接边a存在;如果ya=0,则表示该连接边不存在。
交通需求OD为(qrs)n×n,其中qrs为节点r至节点s的流量。系统优化目标为各车流OD在网络上总的行驶时间费用最小,即车辆运行效率最大。
(1)
xa、ta可通过交通分配得到。约束条件为各交叉口上无车流之间的冲突(见图2~6)。
xa可由下层(用户均衡交通分配模型)求出:
(2)
(3)

2 求解算法
上述模型为双层规划模型,多以启发式算法为主进行求解。但由于该模型中变量种类较多(路段单行或双行;交叉口进口道上禁直、禁左等),难以直接应用已有的数值算法,拟采用遗传算法对模型进行求解。
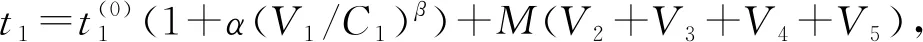
上述模型是有约束的0-1规划模型,可采用遗传算法的0-1编码进行求解。N为所有路段及交叉口连接边的总数目。对以[yz]为决策变量的向量进行0-1编码,其中“1”表示该路段(或连接边)被选择,“0”表示不选。
运用遗传算法进行模型优化求解的算法流程如下:1) 初始化。设定遗传算法的交叉概率、变异概率、种群数目、最大进化代数。2) 采用0-1编码,随机产生初始种群。3) 利用用户最优均衡交通分配算法计算路段及交叉口连接边流量,返回上层计算个体适应度。 4) 对所有个体进行排序选择操作(满足约束的可行解按适应度由高到低排在前面,不可行解按超出约束的大小由小到大接着往后排),选择新种群。5) 按交叉概率对随机配对个体进行交叉操作;6) 按变异概率对种群内个体进行变异操作,位置为0的变成1,位置为1的变成0。7) 判断是否达到迭代总数,若没有,则转入步骤3;否则,输出最佳个体。
3 算例分析
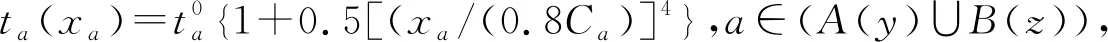
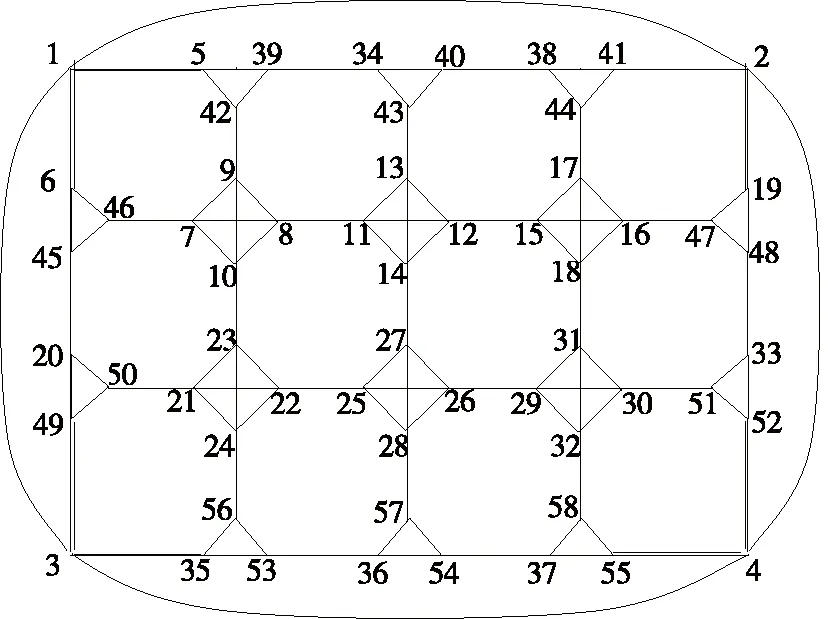
图7 区域网络结构

表1 起终点OD交通分布 辆/h
以遗传算法求解该双层规划模型,种群数取300个,交叉率为0.7,变异率为0.1,程序运行30代得到优化结果。迭代过程见图8,车流组织优化方案见图9,图中无车流流向标识的支路上没有车流。目标函数为1 680 700 s,各路段及交叉口转向边上的流量见表2。
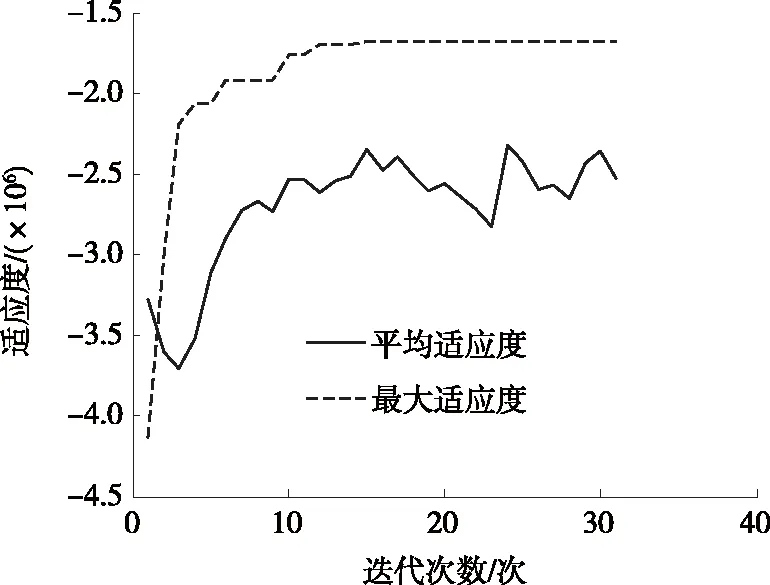
图8 适应度随迭代次数的变化
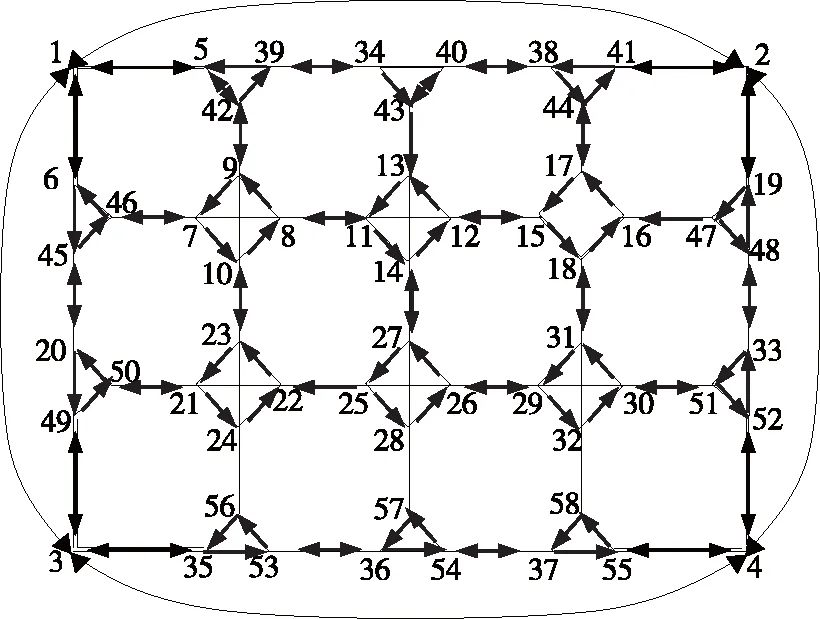
图9 车流组织方案
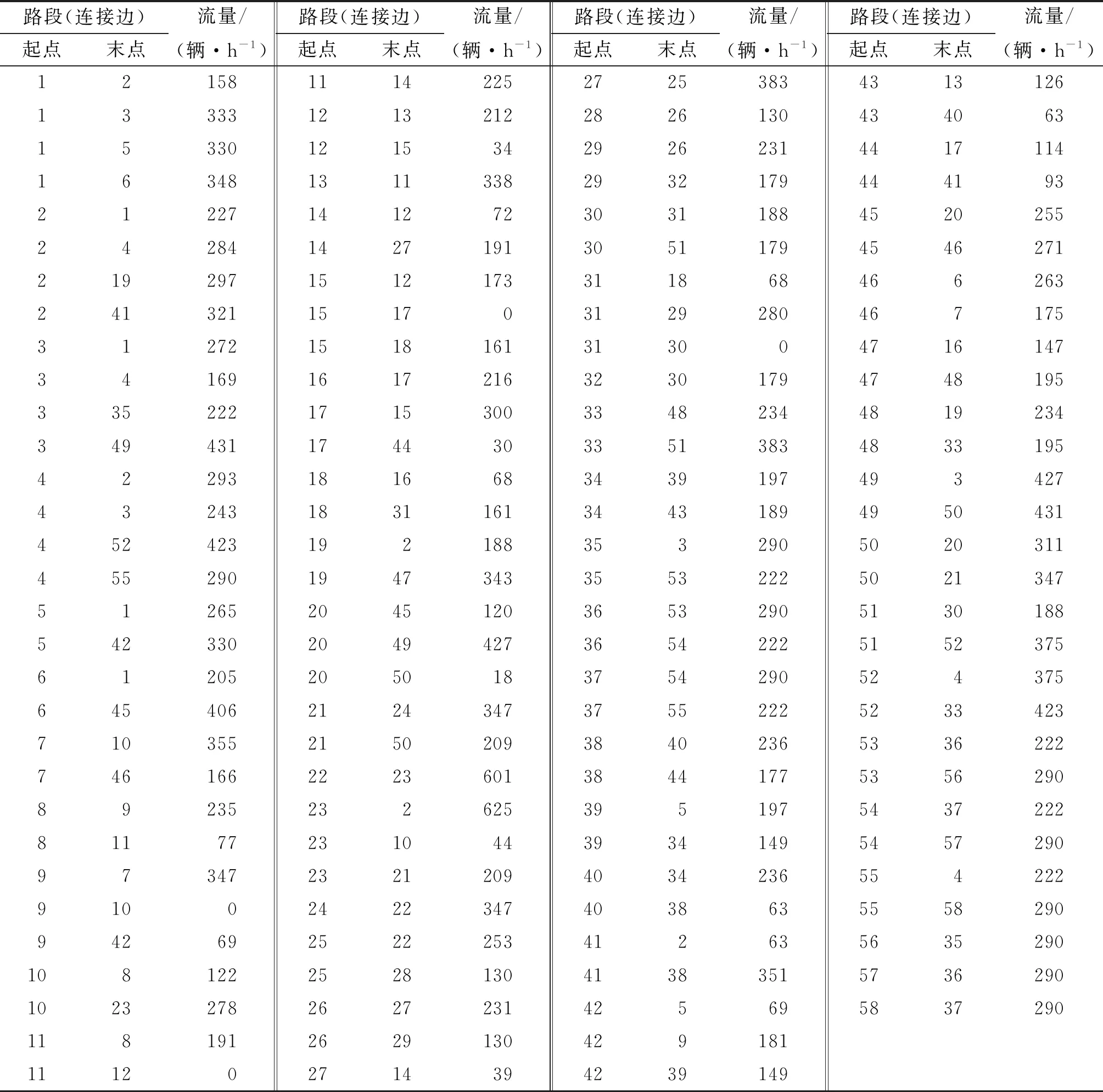
表2 各路段(连接边)的流量
4 结语
针对区域支线网络,设计了在交叉口上无冲突交通流组织的双层规划模型及采用遗传算法对模型进行求解的算法。通过求解模型,得到区域支线网络上各交叉口上禁直或禁左决策方案,并实现总的车流运行时间最小化的目标,算例验证结果表明该模型与算法有效。
