多帧时间窗轮换算法规划仓储多AGV小车路径

2020-12-07陈广锋余立潮

计算机工程与应用 2020年23期

陈广锋，余立潮

东华大学机械工程学院，上海 201620

1 引言

随着智能物流技术的不断发展，在仓储环境中利用自动引导车辆（Automated Guided Vehicle，AGV）或自动引导车辆在传感器及其他智能设备[1]的共同作用下实现自动拣货能够提高企业的核心竞争力和降低人工成本，因此AGV 小车在车间的实现智能路径调度是一个重要的研究课题。

通常情况下，仓储环境中的AGV 小车的工作环境包含静态货架和动态小车，实现小车的运动路径规划需要将几何约束（例如避障）、运动学约束（速度、加速度、边界）和动态约束组合起来转化成复杂的多变量优化问题，研究人员对于复杂的优化问题均采用了耦合和解耦的运动规划方法[2]。耦合的方法考虑简化的环境[3]，但是速度太慢且无法在线使用。因此，大多数采用解耦方法，即运用基于图的方法和基于随机抽样的方法解决预先路径规划，如 A*寻路算法[4]、Dijkstras 算法[5]、蚁群算法[6]、概率路线图（PRM）[7]、基于人工势场[8]。赵江等学者[9]运用几何方法优化传统A*算法规划出距离短且平滑的轨迹，刘新宇等学者[10]采用蚁群聚类自适应方法在动态环境下实现单条轨迹的小车轨迹规划，然而他们均未对较多小车情况下的轨迹规划。Mercy等学者[11]将轨迹规划问题提炼成最优控制问题（OCP），然后提供将OCP 问题转换为链式系统的可行性解决方案。后续路径规划阶段通常使用模型预测控制（MPC）[12]引导小车系统沿着预先计算路径行驶，然而解耦方法在后续路径规划阶段不考虑车辆的运动学及碰撞约束导致计算出的路径通常是不可行的。

对多AGV 小车的控制非常复杂，现有的各种MPC方法不能灵活处理任意（非凸）约束问题和碰撞避免约束[13-15]，而且解决非凸多车问题方法大多局限于解决离线最优控制问题[16-17]。对于现有的DMPC策略以分布式方式通过多次更新解决优化问题[18-19]，通常涉及多次迭代，每次迭代都需要解决局部优化问题和相邻小车之间的通信，由于计算能力和通信能力导致更新太慢。

综上所述，本文提出一种基于多帧时间窗轮换算法，运用A*寻路算法进行全局路径规划，结合B样条的特性保证约束，降低优化问题的变量维度。通过多帧切换以及每一帧建立的目标优化函数扩展小车运动规划中的避障限制，通过运用时变分离超平面的技术实时应对运动规划中环境的不确定性和干扰。

2 问题模型

2.1 问题描述

在仓储作业环境中，AGV 小车在从初始位置移动到目的地旨在解决一个全局最优控制问题，将系统运动学限制和所有动态障碍物体考虑在内，假设AGV 小车模型完全对称的，如图1所示，记小车的轨迹坐标为：

其中，N为小车的数量，χi表示第i辆小车，则q(χi(t))、x(χi(t))、y(χi(t))分别表示第χi辆小车轴中心x方向和y方向所在的位置。

图1 小车模型运动学参数示意图

小车的约束包括动力学约束、运动学约束以及执行机构约束，这是一个非常复杂的综合问题，本文仅考虑基本的运行学约束。假设每辆小车χi从初始位置到达目的地所用的时间为，那么小车χi在t时刻的运行学参数如下所示：

其中，ux(χi(t))为小车χi在x方向的速度，uy(χi(t))为小车χi在y方向的速度，θ(χi(t)) 为小车χi的方向角，θ(χi(t))的导数θ′(χi(t))为小车χi在轨迹点pi的角速度，φ(χi(t))为小车χi车轮的转向角，Lw为小车χi前后轮轴距。因此，小车χi在t时刻的状态为：

引入小车的初始位置和终点位置约束：

为了仓储保证小车能够平稳运行和不发生侧翻，同时能使小车拣货过程定位精度更高，引入小车的速度、加速度和角速度约束：

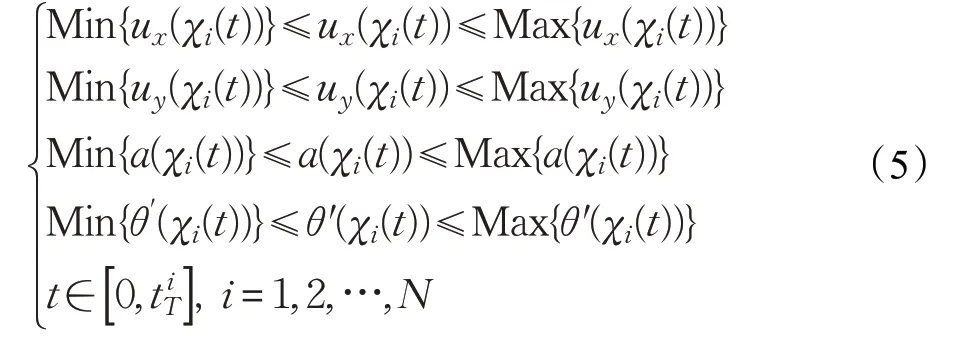
本文研究的仓储环境为结构化环境，如图2所示。

图2 仓储货架结构图

2.2 动态小车防撞约束

多辆小车在运行过程必须考虑小车的防碰撞问题，为了解决这个问题，为每辆小车χi建立线性碰撞模型，该模型能够实时表示出小车每一时刻所在的位置pt(χi(t))，如下式所示：

为了保证每辆小车χi不发生碰撞，即小车的坐标位置在{x,y}∈Rn的二维环境下不会发生重叠，可用如下模型表示：

其中，Pt(χi+k(t))和Pt(χi(t))为相遇两辆小车χi+k和χi在t时刻所在的位置，η为确保小车χi+k和χi保持安全距离的安全系数。实际中多辆小车的轨迹规划问题比较复杂，为了更有效解决上述小车防碰撞模型以及防止小车χi在t时刻所在的位置Pt(χi(t))出现偏差导致的防碰撞模型失效，文献[20]提出可以用最优超平面将两个凸集数据集分成两部分，修正小车χi从t到t+1 时刻的轮廓位置坐标Ωt(χi(t))和Ωt+1(χi(t+1))，如下式所示：

其中，Ωt(χi(t))和Ωt+1(χi(t+1))为小车χi的轮廓四个顶点坐标的集合，R(t)为旋转矩阵。因此，用r(χi)表示小车χi轮廓外接圆半径，小车χi+k和χi在t时刻构造最优超平面方程如下式所示：

小车与过道货架的防碰撞也需要考虑在内，假设货架为规则的矩形形状，矩阵ω表示货架的顶点坐标集合，小车χi在t时刻构造最优超平面方程如式（10）所示。

综上所述，多小车需在满足上述所有约束下实现最优路径规划问题，因此，建立t时刻小车所在的窗体的状态与所在窗体的目标位置状态的一范数的积分为优化模型目标函数，如式（11）所示。目标函数的物理意义是保证t时刻小车所在的窗体的位置状态与所在窗体的目标位置状态的误差最小，为了解决问题的需要，将一范数积分获得具有凸集特征的优化模型目标函数。

3 B样条参数化变量

B样条曲线是个逐段曲线且在连接处可微，其强凸包性质可以进行更精细的局部形状控制。因此，可以采用k次的B样条曲线构造复杂的小车路径，有效地减少变量的维度以及替代上述所有约束。

为了将小车路径q(χi(t))参数化为B 样条多项式曲线，将时间t无量纲为：

已知n+1 个控制点集C={c0,c1,…,cn}和一个节点向量集合U={τ0,τ1,…,τm}，小车路径q(χi(t))可参数化为k次B样条曲线如下所示：

其中，0 ≤l≤n-k-1，1 ≤k≤n-1，规定[0,1]。

根据小车实际路径轨迹规划的需要和B 样条曲线的性质，为了最后计算结果的合理性，选取节点向量集合，通过计算k次B样条曲线的基函数导数，将小车的所有速度和加速度约束转化成k次B样条曲线形式。

因此，通过对B样条曲线系数的控制实现小车约束的转化，将式（2）改写为：

其中，每辆小车χi的速度和加速度约束转化如下：

将超平面方程的系数B样条参数化为：

4 问题模型解决

4.1 多帧时间窗分割

所提算法创新性地将小车置于图3 所示的各种虚线框中，将全局路径规划简化为虚线框局部环境的轨迹规划问题，结合B 样条曲线的性质，保证每个虚线框内小车轨迹的平滑性和运动时间的连续性。在每个虚线框建立小车的运动模型，进而求解每个局部环境小车的轨迹规划问题。小车完成全局轨迹规划需要对多帧窗体进行切换，在同一个虚线框运行的小车数目小于等于1 时，将不用考虑动态避障；当小车数目大于等于2 时，通过设置布尔向量表，控制超平面约束方程的使用，进而保证小车动态运行时实现协同规划。

图3 多帧窗体分割类型

4.2 静态环境小车轨迹规划求解步骤

算法1静态环境小车轨迹规划

步骤1初始化小车的起始位置pstart和小车的终点位置pend，运用网格划分方法计算静态障碍物坐标点集γ=(γ0,γ1,…,γm)，将pstart赋值给当前节点和放置小车轨迹节点的closelist向量表，初始化临时向量表openlist。

步骤2判断小车的起始位置pstart和小车的终点位置pend是否属于静态障碍物坐标点集γ，如果是，修正pstart和pend，重新初始化当前节点和放置小车轨迹节点的closelist向量表。

步骤3判断当前节点周围的8 个位置坐标点是否属于静态障碍物坐标点集γ，如果满足，则退出本次算法；如果不满足，则进入步骤4。

步骤4遍历当前节点周围的8个位置坐标点，遍历向量表closelist，如果当前节点周围的8 个位置第i个坐标点i∈Z 且i∈[0,8]属于closelist，则标记当前节点周围的8 个位置的第i个坐标点为旧的坐标点；遍历向量表openlist，如果当前节点周围的8个位置第i个坐标点i∈Z 且i∈[0,8]属于openlist，则标记当前节点周围的8 个位置的第i个坐标点为旧的坐标点，重新计算该节点较小的评价函数g、f、h；如果当前节点周围的8个位置第i个坐标点i∈ Z 且i∈[0,8]不属于closelist和openlist，则将该位置坐标点放入临时向量表openlist中，创建新的当前节点并将其设置为旧的当前节点的子节点，计算该节点的评价函数g、f、h。

步骤5判断i是否等于8，如果是进入步骤6；如果否则跳回步骤4。

步骤6挑选节点中评价函数f最小的节点作为当前节点，从openlist移除它并把它加入closelist。判断当前位置是否到达终点位置，如果是，则退出程序；否则，跳回步骤2。

4.3 动态环境小车轨迹控制点更新优化策略

如图3 所示，每一时刻每一个虚线框内的小车数目都在动态变化，为了实现多小车轨迹的动态规划，所提算法将对虚线框内小车轨迹控制点进行动态更新，确保各个小车轨迹不发生冲突。因此，构造障碍函数f(τ)更新控制点，将所有不等式约束简化成g(τ)=(g0(τ),g1(τ),…,gm(τ))≥ 0 ，将所有等式约束简化为h(τ)=(h0(τ),h1(τ),…,hp(τ))=0 。根据牛顿迭代法定义Δτk、Δyk、Δzk为牛顿下降方向，获得式（20）拉格朗日方程：

结合式（20）得到式（21）：

其中，Wk为海森矩阵，在固定μ的情况下，运用牛顿迭代法获得一系列最优解组成的集合τ∗(μ)，海森矩阵的引入可以避免出现全局无法收敛。再判断求得的牛顿步长是否满足如式（23）所示的条件。

运用回溯直线法更新牛顿步长，其步长如式（23）所示，当前迭代结束后，运用式（24）进入下一个迭代循环。一旦τ∗(μ)满足设定的误差范围，算法结束。

算法2小车的轨迹控制点更新算法

输入：目标函数f(τ)，不等式约束g(τ)和等式约束h(τ)

输出：小车的轨迹控制点集ψ=(ψ0,ψ1,…,ψn)

1.初始化ε,μ0,εtol,l← 0,k← 0,τ←τ0

2.Repeat

3.do

4.计算式（21）Newton方向Δτk、Δyk、Δzk

5.If 式（22）满足then

6.计算Newton减量λ2(τ)=ΔτkT∇2φμ(τ)Δτk

7.计算回溯直线法确定步长式（23）

8.计算式（24）

9.else

10.break

11.Untilλ2(τ)/2 ≤ε

12.μj+1=1/μ×μj,μ<1

13.Untilmμj+1≤εtol

4.4 算法流程

算法总的流程图如图4所示，其具体步骤如下：

步骤1分割窗体，设置仓储环境参数以及小车变量参数，设置所有窗体切换临界值向量表和超平面临界值向量表，设置采样周期ΔT，设置活动的小车数目。

步骤2遍历所有活动的小车数目，利用4.2 节的结果形成所有活动小车的全局路径离散点，解耦仓储环境参数以及小车变量，获取初始窗体切换临界值向量表，超平面临界值向量表。

步骤3判断当前活动小车数目是否为0，如果为0，则跳转到步骤8，否则跳转到步骤4。

图4 算法流程

步骤4初始化当前帧各小车的起始时间，设置所有活动小车的B样条参数，创建待优化的所有样条控制点符号变量，创建小车运行学约束矩阵和优化模型。

步骤5将算法1 获得的离散点集的起始点作为算法2变量的初值，调用算法2求解含有约束的小车轨迹，提取小车的轨迹点集ψ=(ψ0,ψ1,…,ψn)。

步骤6判断当前所有活动小车是否达到目标位置，如果是，跳转到步骤8，否则跳转到步骤7。

步骤7获取当前帧所有小车最小的时间节点，利用式子qk+1(χi(t))=qk(χi(t))(k+1)ΔT更新下一帧伪轨迹集合qk+1(χi(t))，同时，下一帧伪速度集合uk+1(χi(t))由uk+1(χi(t))=uk(χi(t))(k+1)ΔT得到，跳转到步骤3。

步骤8算法结束，取得最终小车路径轨迹点的集合ψ=(ψ0,ψ1,…,ψn)。

5 算例实验与分析

5.1 参数设置

为验证所提算法的有效性，通过建立可视化环境对小车的最优轨迹规划进行算例仿真。小车的速度、加速度等约束的数值根据小车实际动力学的向心力和静摩擦力公式得到，但在实际上考虑到各小车的质量不同、地面的静摩擦系数不同、转弯半径不同等因素，将模型进行简化，用一定半径的圆代表小车，小车的最大速度和最大加速度约束数值如表1所示。

表1 小车参数

实验中，采用正方形矩形框代表仓储环境，其参数设置如表2所示。

表2 仓储环境参数

因此，将实验的仓储的过道进行窗体划分，划分结果如表3所示，采用该窗体划分有利于算法2路径寻优。实验中采用的B 样条曲线参数化小车路径以及小车的各种约束，选取B样条的阶次k=3，根据m=n+k+1 以及B样条的性质，B样条的节点向量，控制节点n=13。

表3 多帧窗体分割参数 m

5.2 仿真实验分析

5.2.1 静态环境小车轨迹寻优规划

图5（a）是单辆小车运用4种算法仿真结果对比图，其中蓝色虚线为所提算法仿真轨迹，蓝色实线为A*寻路算法规划的小车轨迹，红色和绿色曲线分别为运用文献改进的人工势场蚁群算法[8]和蚁群算法[21]优化后规划出的小车轨迹，图中可以看出所提算法具有较好的平滑性，蚁群算法规划的轨迹较其他算法具有较大的小车曲率，使得小车在转弯处容易发生侧翻。将文献[8，21]算法的参数设置为：迭代代数N=100，种群大小设置为45，启发式因子α=1，β=1，信息素挥发系数p=0.15，信息素强度系数q=1。文献[8，21]算法实验结果的收敛曲线如图5（b）所示，改进的人工势场蚁群算法相对于蚁群算法具有更强的局部搜索能力，但是对于这两种启发式算法是通过多次递归迭代无限逼近全局最优解，所提算法是结合梯度的思想采用二次拟合曲面寻找全局最优解，相对于传统启发式算法线式搜索，本文算法更具有更广的面上搜索能力，使得CPU运行时间更短，同时所提算法的迭代代数是多个迭代的平均值。

图5 各种算法实验结果

图5（a）和表4 的4 种算法实验结果数据所示，在仿真环境中，4种算法均可以达到轨迹寻优效果，文献[21]所提算法在4种算法结果中表现较差，所提算法在最优路径长度比文献[8，21]算法分别优化了3.38%和0.99%，平均迭代数分别优化了20.24%和11.62%，本文算法在CPU 运行时间上具有明显优势，分别减少了51.06%和51.45%，提高了小车轨迹规划的动态响应能力。

表4 4种算法实验结果

5.2.2 动态环境多小车轨迹规划仿真

动态环境多小车轨迹的规划是一个非常复杂的问题，各辆小车的运行情况会出现各种不确定性，实验中将采用5辆小车进行仿真模拟，假设仓储环境是结构化矩形，小车的初始位置和目标位置设置如表5所示。

表5 5辆小车初始位置和目标位置

5 辆小车动态轨迹规划仿真结果如图6 所示，其中小的圆圈代表小车，实线是A*算法规划出的小车轨迹，虚线是所提算法规划的轨迹。从图中可以看出，A*算法规划出的轨迹曲率较不平滑，不利于小车平稳运行，所提算法在实现有效防止静态和动态障碍物的情况下实现小车轨迹合理规划，同时保证轨迹最优。如图6所示，绿色小车和蓝色小车（a）时刻将要发生碰撞，从（b）时刻可以看出蓝色小车自动减缓速度，实现绿色小车平稳通过岔路口。图6紫色小车和红色小车在（a）时刻距离较近，在（b）时刻红色小车先通过岔路口，紫色小车保持速度，防止撞上红色小车。

图6 5辆小车各时刻的位置

为了更好理解所提算法的规划轨迹的合理性，用小车的运动变化关系来理解。5辆小车的速度和加速度随时间的变化曲线如图7 所示，模拟仿真中，设置每帧窗体小车运行的最大时间：30 s。根据图示，图中的速度-时间曲线和加速度-时间曲线均保持均匀变化，速度和加速度的峰值均满足小车运动学的约束，小车可以比较平稳地运动并且加速度的变化幅度不会导致小车发生刚性冲击，满足小车的力学性能。

图7 5辆小车运行速度和加速度随时间变化曲线

表6和表7是上述5辆小车模拟的速度和加速度仿真结果的实验数据，为了与图7曲线数据变化情况保持一致，表中将数据负号表征小车速度和加速度大小，实际中负号代表小车的运行方向。表中的数据符合表2预设的数据范围，由于5 辆小车同时动态运行，增加了小车运行情况的不确定性，导致在小车出现避障过程中出现小车的速度为0，充分说明所提算法能实现动态小车避障功能，实现小车轨迹动态规划。综合图6 和图7分析得知，小车在通过岔路口时，为了防止两小车出现碰撞，其中一小车的速度逐渐减至为0，符合表6出现小车的速度为0 情况。结合图7 和表6 及表7，2 号小车的速度和加速度方差最小，4号车的速度和加速度方差最大，从图7 的曲线变化情况看出2 号小车的变化幅度较小，4号小车的变化幅度较大，但是总体上符合小车的运动学约束。

表6 5辆小车运行速度结果m·s−1

表7 5辆小车运行加速度结果m·s−2

为了更好地理解所提算法对解决多AGV小车路径轨迹规划的有效性，采用更多数量的AGV 小车进行仿真模拟，小车的起始位置和终点位置随机生成。随着小车数量的增加，路段冲突和节点冲突也会呈线性增加，实现多AGV小车的路径规划复杂度增加。如图8（a）到图8（e）的红色框位置所示，框中共有5辆AGV小车，在图8（a）时刻，位于红色框内左侧的蓝色小车向上方向运行将要到达岔路口，位于红色框内中间位置的浅绿色小车紧跟紫色小车向左方向运行，位于红色框内中间位置的深绿色小车紧跟浅绿色小车向右下方向运行，位于红色框内中间位置的浅黑色小车紧向左上方向运行。由图8（b）时刻分析得知，浅绿色小车紧跟紫色小车向左方向直线运行，并未发生冲突，此时，位于红色框内左侧的蓝色小车向上方向缓慢到达岔路口，未与向左方向直线运行的浅绿色小车和紫色小车发生冲突，位于红色框内中间位置向左上方向运行的浅黑色小车与向右下方向运行的深绿色小车相向而行，向右下方向运行的深绿色小车先通过岔路口，使得两车很好地实现避障。由图8（c）、图8（d）、图8（e）时刻分析得知，位于红色框内左侧向上方向运行的蓝色小车在浅绿色小车驶离岔路口时，向右驶入直线过道，随着其他小车平稳地到达终止位置，最终15辆AGV小车在具有25个静态障碍物的矩形网格中实现协同动态规划。

图8 15辆小车各时刻的位置

文献[21]并未讨论多辆AGV 小车协同轨迹规划的避障仿真效果，仅对比了多种算法实现单条路径规划的优化效果；文献[22]能实现AGV 小车的避障效果，但是仅限制在两个目标的约束的路径规划；文献[23]研究不同路网尺寸中各种算法的多AGV的冲突次数和时间的比较，但并未给出最后的仿真效果，无法直观地体现多AGV的协同动态规划结果。因此，由图6～8的多种仿真结果和小车时间曲线的分析，表明所提算法能有效地实现多AGV小车实际路况的轨迹规划和协同动态响应。

5.3 算法性能分析

表8和图9是多辆动态小车轨迹规划仿真中算法参数所得的数据结果。从图中分析得知，5辆小车从起始点到达目标位置总共经历了10 帧的时间窗，每一帧时间窗内小车的轨迹点的更新时间在较小的范围内，表明小车在较短的时间内实现在有动态障碍物情况下小车轨迹的重新规划。因为算法在更新控制点的过程中的时间复杂度接近对数级别，轨迹更新具有较强的动态响应性。图9（a）为所提算法的目标函数值f(τ)，结合式（11）表明在每一帧的时间窗迭代中小车位置和目标位置保持较小的误差，并且每一帧的时间窗迭代中最大值未发生较大的突变，具有良好的稳健性。μ是障碍函数的系数的对数化的结果，图中表明μ满足预设范围，μ的方差s2在较小的范围波动。图9（c）为牛顿下降方向Δτk两次对数化后的结果，每一帧的均值均稳定在10帧中最大平均值的37%以内，没有出现较大波动，可以看出本文所提算法可以比较稳定地搜索最优解，不会出现过大或过小的搜索梯度。