嘉兴市晚粳稻主栽品种的科技进步及产量因素的函数效应分析

姚坚 姚海根 张世玺 李瑾 范文俊 孙达 冯金祥

（1 浙江省嘉兴市农业科学研究院，浙江嘉兴314016；2 浙江省嘉兴市南湖区农作物管理站，浙江嘉兴314051；第一作者：yjjx001@163.com）

嘉兴市地处浙北平原，常年晚稻种植面积在13 万hm2左右，品种类型以密穗型晚粳稻为主。1992 年以来，嘉兴市对晚粳主栽品种实行2～3 年一更新的策略[1]，始终保持品种的增产优势，单产水平大幅提高，全市单季晚稻平均单产由1993 年的480 kg/667 m2提高到了 2017 年的 575 kg/667 m2。

本文应用Cobb-Douglas（柯布-道格拉斯，简称CD）生产函数模型[2]，对12 个晚粳稻主栽品种的科技进步率及其7 个产量因素与产量的效应进行了分析，以期为高产栽培中建立协调的高产群体及今后的新品种选育提供科学依据。

1 材料与方法

1.1 试验材料

以1992 年以来推广种植的12 个晚粳主栽品种的区试结果为分析材料，其中除秀水134、嘉58 为省区试结果外，其余均为嘉兴市单季晚稻品种区域试验汇总资料，性状值为6 试点2 年平均值。品种主栽年限依据，取自嘉兴市农林（经）局1992—2017 年作物分品种面积统计报表。品种主栽定标为年种植面积大于2 万hm2。选择最高苗数（x1）、有效穗数（x2）、齐穗期（x3）、株高（x4）、每穗粒数（x5）、结实率（x6）、千粒重（x7）等 7 个产量因素与产量的效应为分析内容（表1）。

1.2 分析方法

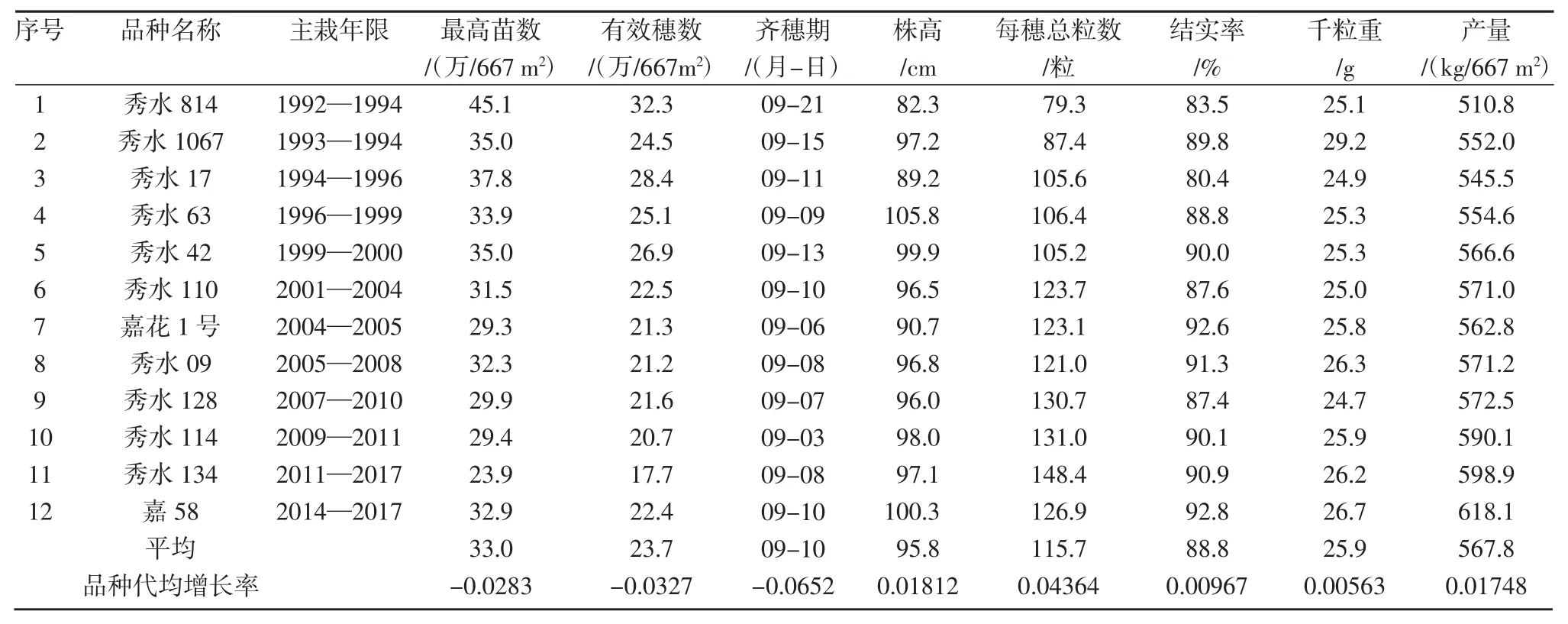
表1 嘉兴晚粳稻主栽品种产量因素和产量数据

弹性系数中，当0＜bi＜1 时，输入因子的输入量为合理阶段，bi＜0、bi＞1 为输入量不合理阶段。当表明系统的生产力处于递增阶段；若表明系统的生产力处于递减阶段。生产弹性系数表示xi输入因子每增加1%，可使输出值增（减）百分率。在求得生产弹性系数后，可求出各输入因子的边际生产力，MPi=bi边际生产力可测定输入因子每增加一个单位量可得到平均产量的增量。

设 y=1nY，a0=1nA0，x1=1nX1，x2=1nX2，…，xn=1nXn，根据最小二乘法原理的计算，即可求得一个多元线性函数模型：y=a0+δt+b1x1+b2x2+…bnxn，进行反对数转换，得到了所求的C-D 生产函数式。

2 结果与分析

2.1 模型的建立

对表1 数据进行对数化处理，按多元线性回归的统计方法，得到多元线性回归方程：y=1.715+0.0074 t-0.0428 x1+0.2620x2+0.0078 x3+0.1522 x4+0.2818 x5+0.0355 x6+0.5214 x7

将多元线性回归方程进行反对数转换，其C-D 生产函数模型为该回归方程经方差分析达极显著水平（F=34.63＞F0.01[8，3]=27.49），D·W=1.999，决定系数 R2=0.9946。表明该函数式与实际生产拟合程度极高，产量变化的99.46%可用模型中的品种序列及7 个变量要素来说明，该模型是合理的。

2.2 因子弹性值分析

由C-D 生产函数模型可知，本资料中主栽品种的最高苗数、有效穗数、齐穗期、株高、每穗粒数、结实率、千粒重的弹性系数分别为-0.0428、0.2620、0.0078、0.1522、0.2818、0.0355、0.5214。7 个弹性系数的绝对值大小顺序为：b7＞b5＞b2＞b4＞b1＞b6＞b3，说明 7 个产量因素对单产的影响是：x7＞x5＞x2＞x4＞x1＞x6＞x3，即千粒重对产量的影响最大，其次为每穗粒数，再依次为有效穗数、株高、最高苗数、结实率、齐穗期[5]。

弹性系数中，0＜b2、b3、b4、b5、b6、b7＜1，表明有效穗数（17.7～32.3 万/667 m2）、齐穗期（9 月 3-21 日）、株高（82.3～105.8 cm）、每穗粒数（79.3～148.4 粒）、结实率（80.4%～92.8%）、千粒重（24.7～29.2 g）等 6 个因素均处于合理阶段；b1＜0，表明最高苗数（23.9～45.1 万/667 m2）处于不合理阶段，其效应显示最高苗数平均水平已偏高。7 个产量因素的弹性系数之和表明本资料范围内主栽品种的产量仍处于递增阶段，协调各因素水平，可发挥更大的高产潜力[6]。

2.3 因子边际生产力分析

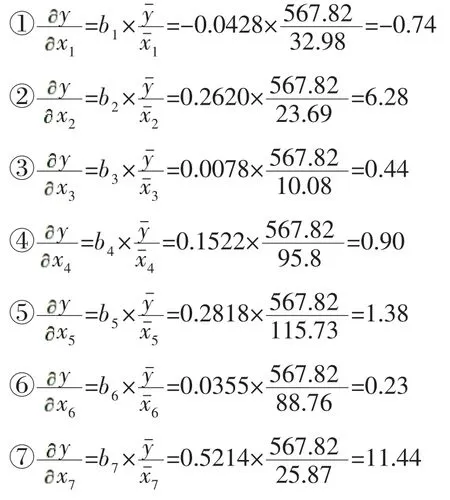
结果表示，在12 个主栽品种中，当输入的其他产量因素在平均水平时，最高苗数每提高1 万/667 m2，单产减0.74 kg/667 m2；有效穗数每增加1 万/667 m2，单产增6.28 kg/667 m2；齐穗期每延迟1 d，单产增0.44 kg/667 m2；株高每增加 1 cm，单产增 0.9 kg/667 m2；每穗粒数每增加1 粒，单产增1.38 kg/667 m2；结实率每提高1 个百分点，单产增0.23 kg/667 m2；千粒重每提高 1 g，单产增 11.44 kg/667 m2。

显然，有效穗、每穗粒数、千粒重、株高等4 个因素的边际生产力较高，对单产的影响最大，是栽培措施上应重点调控的因子[6]，也是新品种选育中应重点掌控的性状因子。

2.4 因子贡献率测算

最高苗（x1） 对单产的贡献率=[（-0.0428）×（-0.0283）]/0.0175=6.93%；

有效穗数 （x2） 对单产的贡献率=[0.2620×（-0.0327）]/0.0175=-48.95%；

齐穗期（x3）对单产的贡献率=[0.0078×（-0.0652）]/0.0175=-2.89%；

株高 （x4） 对单产的贡献率=（0.1522×0.0181）/0.0175=15.78%；

每穗总粒数 （x5） 对单产的贡献率=（0.2818×0.0436）/0.0175=70.36%；

结实率（x6） 对单产的贡献率=（0.0355×0.0097）/0.0175=1.96%；

千粒重（x7） 对单产的贡献率=（0.5214×0.0056）/0.0175=16.79%。

由此可见，各输入因子对产量贡献的份额大小为：每穗粒数（70.36%）＞科技进步（42.33%）＞千粒重（16.79%）＞株高（15.78%）＞最高苗数（6.93%）＞结实率（1.96%）＞齐穗期（-2.89%）＞有效穗数（-48.95%）。显然，品种穗型的逐代增大及育种技术的不断进步，是主栽品种单产不断提高的主要原因。另外还可以看出，有效穗数因子的增产潜力尚未发挥。

3 小结与讨论

本资料中，由C-D 生产函数模型的弹性系数绝对值显示，各因素对主栽品种产量的影响：千粒重（x7）＞每穗总粒数（x5）＞有效穗数（x2）＞株高（x4）＞最高苗数（x1）＞结实率（x6）＞齐穗期（x3）。

弹性系数中，0＜b2、b3、b4、b5、b6、b7＜1，表明有效穗数、齐穗期、株高、每穗粒数、千粒重6 个因素量处于合理阶段；b1＜0，表明最高苗数因素量处于不合理阶段。

从因素边际生产力分析，有效穗数、每穗粒数、千粒重、株高等4 个因素的边际生产力较高，是栽培措施上应重点调控的因子，也是新品种选育中应重点掌控的性状因子。

因子对产量贡献的份额，以每穗粒数最大[7]，其次为科技进步，再依次为千粒重、株高、最高苗数、结实率、齐穗期，而有效穗数为较大的负贡献率，这也表明晚粳稻增产的潜力所在。品种穗型的逐代增大及育种技术的不断进步，是晚粳稻主栽品种单产不断提高的主要原因。今后新一代晚粳稻主栽品种应抓好适宜多穗基础上的大穗选育。