采用双目视觉的非合作空间目标相对导航与惯性参数辨识方法

2020-12-07胡启阳王大轶

宇航学报 2020年11期

胡启阳，王大轶

(1.北京控制工程研究所，北京100190；2.北京空间飞行器总体设计部，北京100094)

0 引言

在轨服务，即利用空间智能服务航天器对目标进行维护，加注，辅助离轨等操作，有助于延长航天器的使用寿命，降低运营成本，对于促进航天事业的可持续发展具有重要意义。许多国家已将在轨服务列为本国航天领域重要的发展方向，并开展对相关技术的攻关[1-3]。在轨服务包括交会，捕获，操作，分离等一系列过程。其中，对目标进行感知测量以获取目标状态与性质的相关信息，是在轨服务过程的关键环节，也是服务航天器对目标接近并实施在轨操作的前提。在轨服务的对象通常属于无应答，无标识，不配合的“非合作目标”。因此，作为在轨服务关键技术，对于非合作目标的测量感知技术具有重要的研究价值和迫切的现实需求。

对于非合作目标的测量感知包括获取表征目标运动状态的轨道姿态动力学参数以及目标固有属性的质量与转动惯量，二者分别属于相对导航和惯性参数辨识问题。相对导航方面，目前的研究多基于视觉测量手段，即利用光学敏感器对目标进行连续观测，并建立目标表面特征与目标自身运动规律的关系，进而设计相应的导航滤波器来实现[4-6]。文献[7]利用激光雷达获得的目标表面点云数据，结合迭代最近点和自适应滤波方法，实现了目标轨道姿态参数和惯量比的估计。文献[8]利用位姿图优化方法消除点云迭代过程中的累计误差，并采用了基于李群的滤波算法。文献[9]利用双目相机观测目标表面的特征点进行相对导航，推导了一般的耦合模型描述姿态运动对位置运动的影响。文献[10]通过考虑相机安装偏置实现利用单目相机对空间碎片的相对位姿估计。针对单一观测精度受限的问题，文献[11]提出了利用多平台观测的方法，并比较了不同的信息融合算法对导航精度的提升效果。以上研究多以非合作目标的惯性主轴描述姿态，由于主轴定义方式的不同，可能导致多解的情况，影响滤波稳定性。同时，对于相对轨道运动多以线性化的方程描述，制约了模型的精度。此外，现有文献多采用轨道姿态同时估计的方法，增加了系统的维数，增加了计算负担，不便于星上使用；惯性参数辨识方面，对于自由旋转的目标，仅依靠视觉测量无法确定目标的质量与转动惯量。因此，改变目标的运动状态是进行惯性参数辨识的前提。目前对于非合作目标的质量和转动惯量的辨识主要依靠服务航天器施加激励来改变目标运动状态，并利用线/角动量守恒或牛顿欧拉法原理实现[12]。文献[13]利用机械臂改变航天器系统的运动状态，同时测量速度与角速度，利用最小二乘法实现全部惯性参数的辨识。文献[14]则将惯性参数辨识转化为一个非线性优化问题，利用粒子群算法进行求解。针对最小二乘法计算量大的问题，文献[15]利用细胞机器人交互来实现分布与异步式的参数辨识。文献[16]建立了机器人末端关节捕获目标的动力学模型，并着重分析了碰撞次数对于参数可辨识性的影响。文献[17]利用柔性杆对目标触碰施加激励实现辨识，该方法需要精确测量杆件施加的力与力矩。可见，目前的辨识方法大多需要服务航天器直接与目标接触，并且一般需要同时测量所施加的激励以及运动状态的改变，因此对于相应敏感器的配置具有一定的要求。同时，外部环境的干扰会影响动量守恒或牛顿欧拉方程的使用。对此，文献[18]提出了一种黏附激励下的惯性参数辨识方法，利用黏附卫星与非合作目标黏附前后速度的变化，结合动量守恒原理实现了目标质量的辨识。黏附卫星技术的成熟，为服务航天器在无需与目标直接接触的情况下实现目标全部惯性参数辨识提供了可能性。

针对上述方法的不足，本文提出一种基于双目视觉的非合作目标相对导航与惯性参数辨识方法。首先利用目标表面的特征点来定义目标的位姿，并分别设计了姿态测量和相对导航滤波器实现姿态轨道参数的估计，增强了算法的适用性，并减少了计算负担。同时，相对运动采用轨道根数的方法进行描述，提高了建模精度。在此基础上，仅利用双目相机结合导航算法对与黏附卫星和目标形成的组合体进行观测，而无需对于激励的测量以及动量守恒的假设即可实现目标质量和转动惯量的有效辨识。

1 基于双目相机的相对导航方法

1.1 坐标系建立

利用双目视觉实现相对导航的问题，涉及双目相机观测量以及相对运动模型的表征。为便于描述，定义如下坐标系：

地球惯性坐标系{I}:原点为地心，x轴指向春分点,z轴指向地球北极，y轴的确定满足右手正交系。

服务航天器轨道坐标系{L}:原点为服务航天器质心，x轴方向沿服务航天器矢径方向，z轴为轨道角动量方向,y轴的确定满足右手正交系。

双目相机坐标系{C}:原点为左相机的投影原点OC，x轴，y轴方向平行于成像平面并正交，z轴沿左相机的光轴垂直于成像平面。

非合作目标几何坐标系{T}:根据相机观测结果进行建立，并与非合作目标相固连，是描述非合作目标姿态运动的基准。其具体定义方法见下文。

1.2 基于双目视觉的位姿测量

双目相机对非合作目标进行连续观测，并通过图像处理技术识别和跟踪非合作目标表面的N个特征点。

图1 基于双目视觉的位姿测量示意图

对于任意特征点Pi，i=1,…,N，其在相机左右相平面上的投影像素坐标分别为(uli,vli)和(uri,vri)。根据双目相机的三角测量原理，可以恢复相机坐标系{C}下特征点的坐标ρi，公式如下：

(1)

需要指出，一方面由于特征点直接利用图像处理算法获得，在分布上具有一定的任意性。另一方面，考虑到目标的非合作特性，特征点相对于目标的相对方位未知。因此有必要利用所获得的特征点，建立相应的几何坐标系，作为描述目标位置与姿态的基准[19]。假定已经获得了三个特征点P1，P2，P3，其在相机坐标系下的坐标根据式(1)分别为记为ρ1,ρ2,ρ3，则可以根据式(2)得到一组满足右手定则的单位正交向量c1,c2,c3。

(2)

以特征点P1为原点，单位正交向量c1,c2,c3为基矢量，可建立与目标相固连的几何坐标系{T}。{T}与相机坐标系{C}之间的方向余弦矩阵RTC的各列由基矢量的坐标组成，即

(3)

1.3 姿态测量滤波器

利用以上几何坐标系的建立方法，仅能获得离散时刻的几何坐标系的测量值，并且容易受单次测量噪声的影响。通过姿态测量滤波器，不仅可以获得受噪声干扰较小的连续估计值，并且能够进一步估计角速度和惯量等姿态运动参数。

假定目标为在空间中自由运动的刚体，当用四元数qTI描述其相对于惯性坐标系的姿态时，满足如下的姿态运动学方程。

(4)

式中

(5)

同时，假定目标姿态不受主动力矩控制，处于自由翻滚状态，则其角速度满足如下的欧拉方程。

(6)

式中:ε是环境力矩引起的噪声，可建模为零均值的高斯白噪声。I矩阵是目标惯性张量在几何坐标系下的展开形式。由于几何坐标系的建立具有任意性，不失一般性，可以写为如下包含惯量积的形式。

(7)

(8)

将式(8)代入(6)并进行整理，可得

(9)

l=[Iyy/Ixx,Izz/Ixx,Ixy/Ixx,Ixz/Ixx,Iyz/Ixx]T

(10)

作为表征惯量的参数，并满足如下公式

(11)

根据上述分析，可以建立起姿态测量滤波器的结构：被估计状态为几何坐标系的姿态，角速度以及惯量比矢量，其动力学方程分别满足式(4)(9)(11)。

(12)

滤波器的测量为几何坐标系相对于惯性系的姿态四元数，可以按下式计算得到：

yr=qTI=qTC⊗qCI

(13)

式中:qTC为式(3)所求方向余弦阵对应的姿态四元数，是构建几何坐标系{T}的直接结果。qCI为相机坐标系相对于惯性系的姿态四元数，可由服务航天器自身的姿态结合相机的安装方位获得。

1.4 相对导航滤波器

在相对导航的过程当中，为了确定目标的轨道，需要描述目标质心相对于服务航天器的运动规律。现有文献，对于目标进行相对运动的描述，多基于轨道坐标系下的相对位置，速度来描述，如CW方程，TH方程等等。上述方程在推导的过程中均进行了近似，并且对轨道的构型具有一定的要求。

由于惯性参数辨识需要对目标质心进行精确的估计，因从本文采用轨道根数的建模方法，一方面形式简单精度较高，另一方面适用范围更广。考虑到近距离相对导航的过程中观测时间较短，因此不考虑轨道摄动的影响。此时，二者的轨道根数具有以下简单的演化形式。

(14)

式中:μ是引力常数。a是轨道半长轴，e是轨道偏心率，i是轨道倾角，Ω是升交点赤经，ω是近地点幅角，M是平近点角。

本文采用如下形式的相对轨道根数δxœ表征目标与服务航天器的相对位置

(15)

式中:u=M+ω是平纬度幅度。下标t/s表示该轨道根数分别属于服务航天器/目标。

考虑到服务航天器自身的轨道根数œs已知，相对轨道根数的演化过程可写为如下形式的非线性方程。

(16)

由于几何坐标系选取的随机性，不失一般性，可将目标质心位置在几何坐标系{T}下的坐标为r为待估计的参数，并满足

(17)

在此基础上，在相机坐标系{C}下几何坐标系{T}的原点位置可表示为，

p=RCLρ+RCTr-d

(18)

式中:d是相机安装位置相对于服务航天器质心的偏置，RCL是轨道坐标系{L}相对于{C}的方向余弦阵，二者均可视为已知。ρ是目标质心相对于服务航天器质心在轨道坐标系{L}下的表示，其与相对轨道根数的关系可利用轨道根数与惯性系下位置和速度的对应关系获得，并记为如下非线性函数形式

ρ=g(δxœ(t))

(19)

根据上述分析，可以建立起相对导航滤波器的结构：待估计状态包括相对轨道根数和质心偏置，其动力学方程分别为式(16)(17)，

(20)

(21)

式中:符号*表示四元数求逆。R(q)为四元数q对应的方向余弦矩阵，按以下公式计算：

(22)

式中:q0和qv=[q1,q2,q3]T分别为四元数的标量与矢量部分，I3为单位矩阵。

整个相对导航算法流程如下：

图2 相对导航流程图

2 基于相对导航的惯性参数辨识方法

黏附卫星是随着微重力环境技术发展而出现的具有黏附能力的新型飞行器，在与目标接触后可黏附在其表面形成一个整体。基于相对导航的惯性参数辨识方法，需要已方的航天器去黏附非合作目标。利用相对导航对于质心和惯量比的可测性，可以实现非合作目标质量和转动惯量的估计。

图3 黏附后组合体质心变化示意图

2.1 基于视觉导航的组合体质心估计方法

假定黏附后形成的组合体为刚体。因此，可以利用前面提出的相对导航方法，对组合体的姿态，角速度，惯量比以及质心进行估计。

2.2 基于质心变化的质量辨识方法

黏附之后，由于组合体的质量分布发生变化，因此其质心的位置也相应改变。由于黏附卫星为已知的合作目标，可以利用表面安装的信标结合双目视觉得到黏附卫星质心B，进而计算其在几何坐标系下的分量rOB。同时，根据相对导航的估计结果，非合作目标的质心A与黏附后组合体的质心C在几何坐标系下的坐标分别为rOA和rOC。基于刚体假设，组合体的质心理论上应当在黏附卫星与非合作目标各自质心的连心线上，且相对于二者质心的距离和各自质量成反比。因此，非合作目标质量可按以下公式进行辨识

(23)

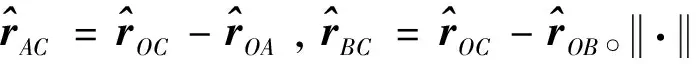
2.3 根据平行轴定理的转动惯量辨识方法

如前文所述，当黏附之后，组合体质心位置发生了改变。根据平行轴定理，组合体关于质心的转动惯量满足如下等式，

(24)

式中：IA和IB分别为非合作目标和黏附卫星对于各自质心的转动惯量矩阵。将与非合作目标质量分布无关的量定义为

(25)

则式(25)可以记为

(26)

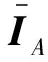
(27)

进而可以得到如下Ixx辨识公式

(28)

3 仿真验证

本节对所提出的相对导航和惯性参数辨识方法分别进行验证，以相对导航的精度作为惯性参数辨识的测量精度。

1)相对导航方法验证

相对导航算法相关参数设定如下：服务航天器的初始轨道根数a=7080 km,e=0.001,i=98.2°,Ω=189.9°,ω=0°,M=0°。姿态测量滤波器的初始方差，过程噪声和观测噪声分别Pr=0.1×I12，Qr=10-10×I12，Rr=10-4×I4。相对导航滤波器的对应参数分别为Pr=0.1×I9，Qr=10-10×I9，Rr=10-4×I3。以上各式中In表示n阶单位矩阵。各变量真实与滤波初始值如表1所示。仿真时间1000 s,测量频率1 Hz。为提高数值稳定性，采用平方根形式的容积卡尔曼滤波算法。

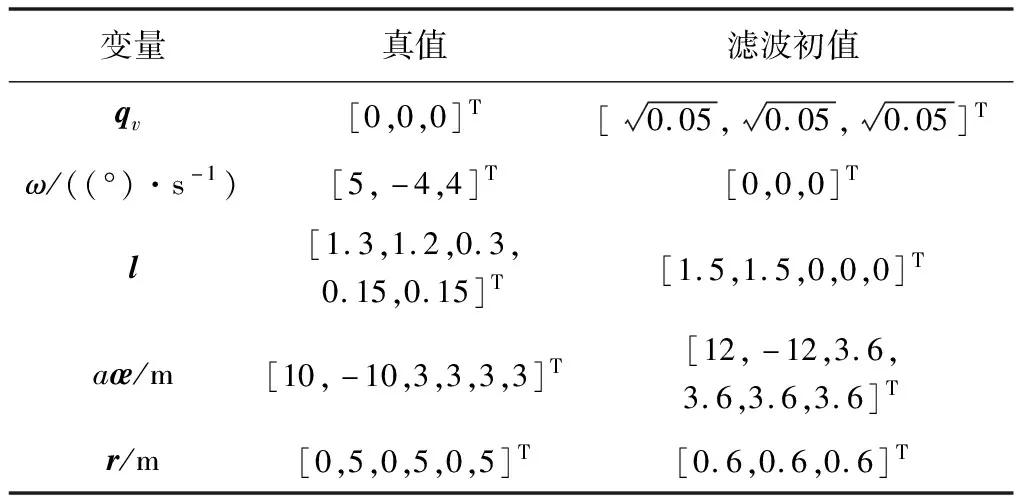
表1 滤波初值设定

相对导航仿真结果如图4所示。其中，四元数的估计误差取误差四元数的矢量部分。对称分布的虚线为估计误差的协方差值(3σ)。由于数据类似，四元数，角速度和质心位置只提供单轴估计结果，惯量比提供Iyy/Ixx的估计结果，相对轨道根数提供aδa的估计结果。

图4 相对导航估计误差

根据仿真结果可见，大概200 s左右，相对导航系统的被估计参数均可以收敛到真值左右。误差基本在估计误差协方差以内，说明滤波算法的一致性较好。为了进一步分析导航精度，进行100次蒙特卡洛仿真，得到的估计精度(1σ)分别为：四元数单轴精度0.002，角速度单轴精度0.03(°)·s-1，质心位置单轴精度0.002 m，惯量比精度0.002, 相对轨道根数精度0.02 m。以上结果表明，所提出的基于双目相机的导航方法可以实现目标姿态，角速度，惯量比，轨道，质心位置等的有效估计。其中，质心位置和惯量比的高精度估计，是后续实现目标质量和转动惯量辨识的前提。

2)惯性参数辨识方法仿真验证

在实现相对导航的基础上，本节验证所提出的惯性参数辨识方法。为了简化问题，假定黏附卫星的质量全部集中于质心。基于上述假设，结合根据式(24)可知，当非合作目标的质量与惯量分布确定之后，相应的辨识结果主要取决于所使用的黏附卫星的质量以及形成组合体后黏附卫星与非合作目标质心的距离。因此，有必要研究以上因素对于辨识精度的影响。

令非合作目标质量为M=1000 kg，x轴的转动惯量为1000 kg·m2。据上文中相对导航算法的仿真结果，设定惯量比和质心位置的测量精度分别为0.002和0.002 m/s。图5和图6分别为通过1000次仿真得到的不同的黏附卫星质量和质心间距下非合作目标质量与转动惯量辨识精度。其中，黏附卫星的质量变化范围从目标质量的0.1倍到10倍，质心间距的变化范围从0.1 m到10 m。惯量比和质量的相对误差精度分别按Δk/k和ΔM/M计算。

图5 黏附卫星质量对于辨识精度的影响

图6 质心间距对于辨识精度的影响

仿真结果表明，从变化趋势上看：对于转动惯量的辨识而言，当黏附卫星质量以及质心间距较小时，辨识误差较大。而当上述两个变量逐渐增加，辨识精度迅速提高。而随着质量和间距的进一步增加，辨识精度又缓慢下降。这是因为本文所提出的对于惯性张量的辨识方法是建立在黏附前后的惯量比的变化之上。当黏附卫星的质量或黏附后的质心间距较小时，惯量比的变化较小；而随着上述参数的进一步增加，根据式(24)，组合体的转动惯量主要由质心变化后各自质量产生的惯量组成，目标自身的转动惯量所占的比重减小，对于组合体惯量比的贡献减小。而以上两种情况均会降低目标的辨识精度。对于目标质量的辨识而言，随着质心间距的增加，辨识精度逐渐增加。这是因为对于目标质量的辨识依赖于黏附前后质心位置的变化。而当质心间距越大，质心位置的变化越明显，因此精度会提高。而对于黏附卫星质量的增加，质量辨识精度呈现先增加，后减小的趋势，并且当二者质量相等时辨识精度最高。辨识精度方面：当黏附卫星的质量与目标质量的比值大于一定值以后，目标质量与惯量的辨识精度所受的影响较小。当质心间距1 m时，转动惯量相对误差2%以内，目标质量相对误差可以达到1%以内。

仿真结果说明，本文提出的质量与惯性参数辨识方法精度较高，并且对于黏附卫星质量，以及黏附点位置的鲁棒性较好，适合工程应用。