摇摆试验台的多系统并联仿真与试验研究

韦作霖，陈冠宇，王利娟

(1.镇江赛尔尼柯自动化有限公司，江苏 镇江 212009；2.江苏科技大学，江苏 镇江 212003)

0 引言

20世纪60年代，英国学者开创了六自由度并联运动机构的研究。经过近60 a的研究与发展，这一研究已在机械工程、计算机科学、软件工程、控制工程和系统仿真等多学科得到了发展，成为进行多学科研究的理想载体[1-2]，在航天、航空、海洋装备的开发上起着越来越重要的作用。

海浪载荷对于船舶甲板机械和船载设备运行的可靠性及寿命都有着显著影响，对设备运行的可靠性和正常作业操作带来的不利影响必须在上船前得以解决，因此甲板机械与船载设备的开发者们多年来一直寻求一种能在陆上检验其开发设备上船运行性能的模拟平台。六自由度并联运动平台可通过波浪谱信号，实时控制6个液压缸的并行工作、协同6个液压缸的伸缩，模拟海浪给船舶造成的姿态变换，从而实现在陆上检验甲板机械和船载设备在海上风浪环境下运行的可靠性[3-4]。依据此原理开发的六自由度液压并联摇摆实验台系统，具有多变量、强耦合、非线性等特点，其控制与系统运动空间设计难度较大[5]。由于系统平台的仿真模拟涉及液压、控制与机械运动姿态等多个并发的工作机制，因而目前尚无一套完整的仿真软件能够胜任这一工作。能够进行液压、控制和机械运动姿态仿真的商用软件AMESim、MATLAB和ADAMS彼此间存在孤岛效应，只能在其软件自身的工作能力范围内，研究系统的某一特征，很难做到全面、准确、有效地运用上述3个学科领域的关联运行参数，分析整个平台运动机构的运动姿态与受控状态。为此，本文依据波浪谱数据对摇摆实验台的液压系统伺服驱动控制要求，结合PID传递函数控制算法，将ADAMS、AMESim与MATLAB的Simulink软件构建成相互耦合的并行仿真系统，对摇摆实验台的六自由度并联机构的机械、液压和控制多个系统进行并行耦合模拟仿真，得到摇摆试验台的PID伺服精度控制的传递函数模型，并利用实物平台实验，验证其控制传递函数模型的精度，为利用多种海况波浪谱数据模拟控制摇摆实验台的运动系统开发奠定基础。

1 摇摆实验台并行仿真模型

1.1 摇摆实验台并行仿真原理

并行摇摆实验台分3个系统，即运动系统、液压系统与控制调节系统。3个系统间通过强耦合形成六自由度闭环平台，因此很难通过对单一的系统建模，获得系统整体的运动与受控状态特性；软件功能的单一性与信息孤岛特征，也很难支持软件间的并行仿真。只有对各系统联合建模，并使得模拟运动、液压与控制的软件进行并行联合仿真，方能获得系统的精确控制模型，使开发的系统控制单元能够控制平台机构运行得更平稳，在接受到海浪模拟信号后能逼真模拟船舶在海浪中的运动状况。

基于MATLAB/Simulink仿真为主的ADAMS、AMESim、MATLAB/Simulink并联仿真系统是一种利用软件间彼此控件进行传递函数数据转移的传递仿真过程。MATLAB/Simulink将对ADAMS中的六自由度并联运动平台的PID控制传递函数通过ADAMS/Control接口输入至ADAMS，控制六自由度并联运动平台的运动，同时ADAMS中的六自由度并联运动平台又将其机械运动的反馈动力学模型函数，通过ADAMS-Sub接口反馈到MATLAB/Simulink中。AMESim与MATLAB/Simulink之间则是将AMESim模型编译为S-Function导入至MATLAB/Simulink中，进行压力驱动传递函数的转移，MATLAB/Simulink依据ADAMS中六自由度并联运动平台动力学模型的反馈信息，将PID控制函数输入至AMESimD液压源的控制环节(阀)，形成液压元件驱动介质的流量、压力和杆件位移量函数，同时该函数的输出量又输入至ADAMS中，控制六自由度并联运动平台各角点的位移、速度、角加速度模拟，在仿真系统中形成闭环。其原理见图1。

图1 摇摆实验台联合函数传递运动与控制仿真原理图

AMESim输出的液压驱动力函数为ADAMS的机械子模型提供了输入动力的函数，从而驱动液压缸运动。输出液压缸位移和速度信号的函数反馈给Simulink中，作为PID控制模型的输入传递函数。其反解算法和控制系统自动依据反馈得到的参数和负载进行PID控制。输出的传递函数传递到AMESim中，形成电液伺服阀控制信号，控制AMESim模拟的液压缸输出相应的液压驱动力与伸缩长度函数，该函数再驱动整个摇摆实验台系统模型完成持续的并联运动仿真。

1.2 ADAMS运动仿真系统机构模型

六自由度液压并联摇摆实验台机构主要包括：上平面动工作平台、下平面静平台、上平面摆动液压缸驱动机构、电液伺服阀控制系统、液压动力恒定驱动站等。工作平台与静平台间通过上、下2组各6个球铰链与6个液压缸柔性并联相接，实现工作平面在6个液压缸的协同驱动下，绕其最大空间包络6个自由度方向运动[6-8]，见图2(a)；图2(b)为导入ADAMS的SolidWorks建立的三维几何模型。将六自由度液压并联摇摆实验台的球铰、液压缸活塞的几何模型在ADAMS内定义为旋转副、移动副，建立起单分量的力矩与输入/输出变量传递函数，再将形成的ADAMS-Sub控制模型传递函数导入至MATLAB中，使ADAMS-Sub接受模拟的液压缸驱动力传递函数，输出活塞杆的速度与位移函数。文献[9]讨论了摇摆台的工作平台在空间上的姿态变化的受控情况，通过反解求出各液压缸的伸缩长度传递函数。在MATLAB/Simulink中建立六自由度液压并联摇摆实验台工作平面的反解传递函数(见图3)，分别给定工作平台6个自由度上的运动约束的最大包络空间，得到各液压缸工作长度变化规律的传递函数[10]，并将此函数反馈到Simulink反解器中求解，形成AMESim中动态伺服阀、液压驱动力与液压缸伸缩控制传递函数信号。

图2 六自由度液压并联摇摆实验台实物模型与机构模型

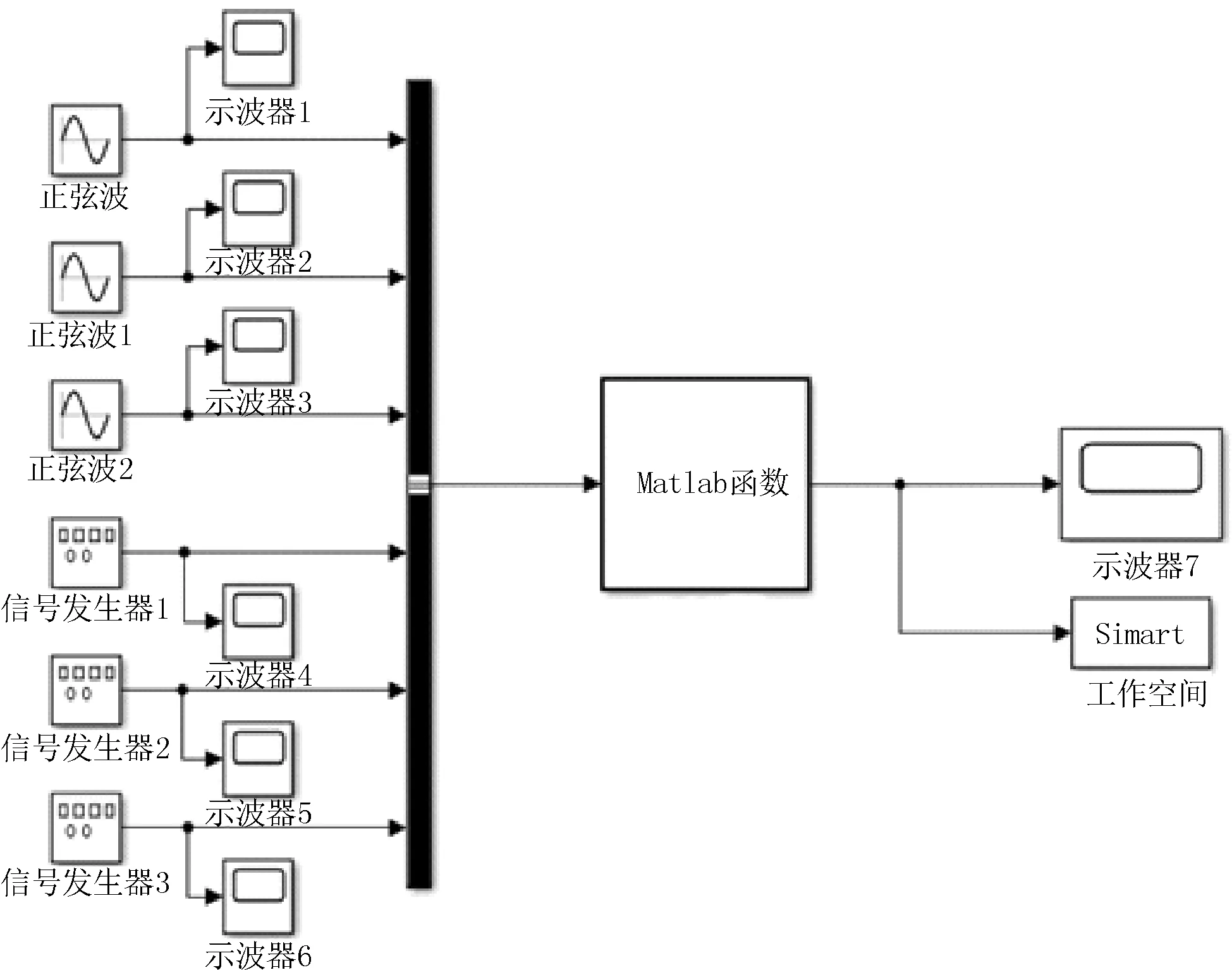
图3 摇摆平台运动学反解Simulink仿真模型

1.3 AMESim液压系统子模型

摇摆试验台由6组对称电液伺服阀控制的非对称缸构成，并且参数相同。系统中最重要的控制元件是电液伺服阀，控制着相同运动仿真的进行。系统选用CSDY1-30型电液伺服阀，参数为：额定流量30 L/min，压降20 MPa，频率85 Hz，阻尼比0.8。

通过在AMESim中建立摇摆试验台6个液压缸在六自由度空间内的液压并联驱动传递函数，将AMESim生成S-Function接口文件中的传递函数引入到Simulink中，就可通过MATLAB/Simulink的PID控制传递函数模型仿真控制AMESim的6个液压缸仿真运行。

1.4 MATLAB/Simulink反馈控制系统模型

1.4.1 位移及反解算法

位移及平台角点空间位置反解算法将摇摆试验台空间6个自由度的位姿反解成6个液压缸的伸长量传递函数，控制模块依据反解得到的液压缸伸长量传递函数控制平台运动，以跟随给定的输入传递函数信号模拟船舶运动。

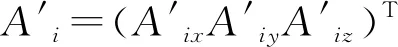
当工作面运动时，上下对应铰支点间距离传递函数li计算公式为：

液压缸伸缩量传递函数为：

Δli=li-l0

式中：l0为液压缸初始长度，m。

1.4.2 MATLAB/Simulink反馈控制系统

MATLAB/Simulink反馈控制包括：期望输入函数、反解函数、PID控制策略函数；AMESim控制通过S-Function函数，其对ADAMS中的几何模型控制通过ADAMS-Sub接口，将运行输出的压力、位移数据传递给ADAMS，见图4。在系统中加载模拟海浪波长的正弦信号作为期望输入函数，通过反解控制算法函数，将工作平台位姿信号反解为液压缸位移量函数信号，通过PID反馈，输出伺服阀控制函数，得到经过整定的模拟PID调节的3个环节的增益Kp=1.125 400；Ki=0.725 290；Kd=0.008 672。

3个软件并行运行间的数据分别通过ADAMS，AMESim导入至Simulink中ADAMS-Sub和S-Function 接口实现，其中PID反馈输出函数控制AMESim的伺服阀开度，输出控制液压缸运行的位移与速度，对摇摆实验台并联六自由度液压系统进行全面的机械、液压、控制并行仿真。

2 摇摆实验台联合仿真及实验

2.1 摇摆实验台联合仿真

构建好3个软件平台并联关系传递函数后，以MATLAB/Simulink作为初始触发平台进行多系统并联仿真。为验证仿真对模拟的海浪波谱的跟随性能，给系统施加正弦信号进行跟踪仿真实验。输入400 mm幅值、频率0.3 Hz的正弦波信号，当工作平台沿Z轴方向正弦运动时，强耦合会造成平台运动的对称性，因此，六个液压缸运动状态保持一致。通过仿真可在Simulink中得到液压缸伸缩量随时间变化的响应函数，1号液压缸正弦响应仿真见图5。

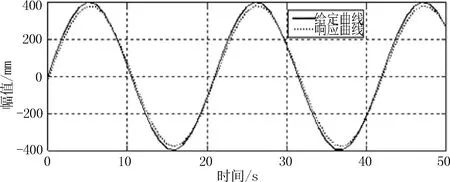
图5 1号液压缸正弦响应仿真图

从图中看出，虽然液压油的阻尼特性会使执行机构产生滞后，但通过多系统并联仿真，在控制系统设计上充分考虑了惯性环节的滞后因素，因此开发的液压系统对正弦信号跟踪特性较好，误差约为3%，跟踪稳定时滞后约为0.02 s。此误差对于液压系统可忽略不计，仿真结果满足平台使用要求。

2.2 摇摆实验台平台验证实验

对摇摆实验台并联六自由度液压系统进行实机操作，以检验通过多平台软件并联仿真建立的反馈控制模型正确性。实验平台由液压泵站控制柜、液压伺服泵站和六自由度摇摆实验台组成，控制柜依据控制系统反馈调节函数输出电流信号，控制电液伺服阀的开度及通断时间，实现对液压缸的位移控制。液压系统的驱动通过液压泵站，在变频电机、定量泵、蓄能器的调节下输出恒压，为系统提供工作压力。选择摇摆实验台并联六自由度液压缸沿Z轴方向进行正弦运动为传递函数的输出，观察6个液压缸的运动状态，在LabVIEW中搭建对1号缸伸缩量变化实时监控界面，检测其工作平面运行状况。

图6为1号缸伸缩量的实际变化值与理论值变化曲线。从图中可以看出液压缸运动时其伸缩量的实际值与期望值存在一定的超调误差，这是由于电压对电磁阀开度增加而导致输出流量呈比例增加。图中伺服阀的开度变化导致瞬态下液压缸压力峰值的增加，使系统产生位移超调量，并在液压阻尼的作用下，上升时间、下降时间和过度时间均滞后于理想状态，但误差在允许范围之内，液压缸具有较好的正弦运动跟随特性。

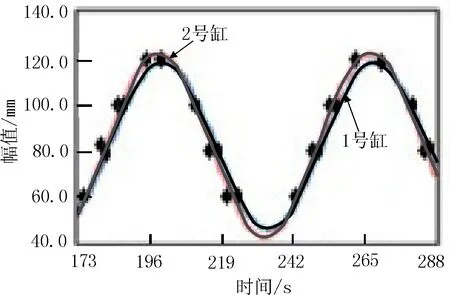
图6 1号缸伸缩量实际值与期望值

平台在周期运动实验前，要将平台垂直上升到中位进行初始化，通过平台的垂荡阶跃响应。以垂荡阶跃位姿轨迹作为实验输入信号，给定系统压力5 MPa、油温25 ℃分别进行PID为控制策略的垂荡阶跃运动，平台垂荡运动时6个液压缸运动状态一致。表1为PID控制策略下垂荡阶跃各缸响应分析，可见在此控制策略内，系统的平均上升时间为3.95 s，平均超调量为7.63 %，平均稳态误差为0.47 mm。满足系统设计要求。

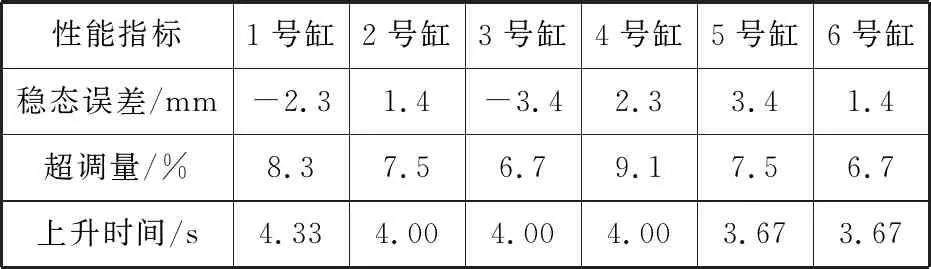
表1 PID控制垂荡阶跃各缸响应分析

3 结论

针对摇摆试验台，利用ADAMS、AMESim和Simulink软件，成功实现了对机械、液压和控制系统的多平台同步并行仿真。得到结论如下：

(1)根据并行仿真的结果，表明设计开发的实验台控制系统可以较好地跟随给定位姿信号，系统控制精度较好，平台运行平稳、安全。

(2)利用联合仿真的方法，研究电液伺服控制系统的动态特性可以更真实、准确、高效地反映物理平台的真实控制与运动状态，能够通过可视化模拟平台的运动，使其运动空间更加清晰直观，从而为开发多自由度的并行机构提供了有力的手段与方法。

(3)通过进一步改进控制策略，如采用Fuzzy-PID策略，可以进一步减小系统的超调量，使系统运行得更加平稳。