混合整数规划与匈牙利法的自动化立体仓库货位优化研究

宋紫浩 张水旺 鲍蔷

摘 要：针对自动化立体仓库货位优化问题，在常规存储策略的基础上，依据周转效率最高原则建立了合适的货位优化数学模型，同时将0～1整数规划原理引入模型求解过程，据此建立整数规划模型，并利用实例数据进行计算。结果表明，在模型求解过程中引入0～1整数规划思想，再利用匈牙利法求解使得原模型求解大大简化，结果也是全局最优，是解决货位优化问题的优良方法。

关键词：自动化立体仓库;货位优化;整数规划;匈牙利法

中图分类号：F253.4;F224文献标识码：A文章编号：1003-5168（2020）28-0051-04

Research on Space Optimization in Automated Warehouse Based

on Integer Programming and Hungarian Method

SONG Zihao ZHANG Shuiwang BAO Qiang

（School of Management Science and Engineering， Anhui University of Technology，Maanshan Anhui 243032）

Abstract： Aiming at the problem of space optimization in automatic three-dimensional warehouse， on the basis of conventional storage strategy and according to the principle of maximum turnover efficiency， an appropriate mathematical model of space optimization was established， and the principle of 0～1 integer programming was introduced into the process of model solving. Based on this， the integer programming model was established， and the calculation was carried out with the example data. The results show that the introduction of 0～1 integer programming in the process of solving the model and then using Hungarian method to solve the original model greatly simplifies the solution of the original model， and the result is also global optimal， which is an excellent method to solve the problem of freight location optimization.

Keywords： automated warehouse;space optimization;integer programming;Hungarian Method

为了提高仓库的存储量和作业效率，自动化立体仓库越来越普遍，其货物存储策略问题也逐渐成为企业家和学者关注的热点问题。一般来说，常规的存储策略主要包括随机、分类、分类随机、定位和共享存储五种。目前，大多自动化立体仓库采取的是随机存储策略，但当货品种类日益增多以及订单量增加时，会造成储位混乱，大大提高存储管理成本。因此，研究自动化立体仓库货位优化问题，以提高仓库的出入库效率、降低存储成本尤为必要。

国内外学者纷纷对货位优化问题进行了大量的深入研究。Elisa FM 等人通过按顺序索引分析所需的空间和总顺序采摘距离的帕累托最优计算，提出了一种基于类的存储过程和存储位置分配方法[1];侯忠和郑国华针对汽车配件库货物的特点，建立了基于货位优化的多目标规划模型[2]，但只对仓库单排货架上的货物进行了货位优化;李永伟等人将货位优化问题分为货位选择层和货位顺序层，建立了以工作人员行走总路程最小为目标的普通立体仓库货位优化模型[3];高楠等人以入库效率、货架稳定和能耗为目标构建了多目标货位优化模型，并采用遗传算法对问题进行了求解[4];徐伟华等人同样采用遗传算法，求解了自动化立体仓库货位分配优化问题[5];Shuiwang Zhang等人构建了以货物稳定性、出入库能耗和货物关联规则的货位分配模型，并采用人工鱼群算法对算例进行了求解，验证了文中所提模型和求解算法的可行性和优越性[6];郭娟等人则采用粒子群算法求解了以货架中心最低（货架稳定性）、拣选路径最短和出入库效率最大为目标的立体仓库货位优化多目标模型[7]。

现有研究中，多数在货位分配模型求解阶段采取算法求解，本文则将货位分配的问题看成是整数线性规划问题中的指派问题，建立货位优化模型后，将其转化为指派问题求解，从而得到最优解決方案。

1 问题描述

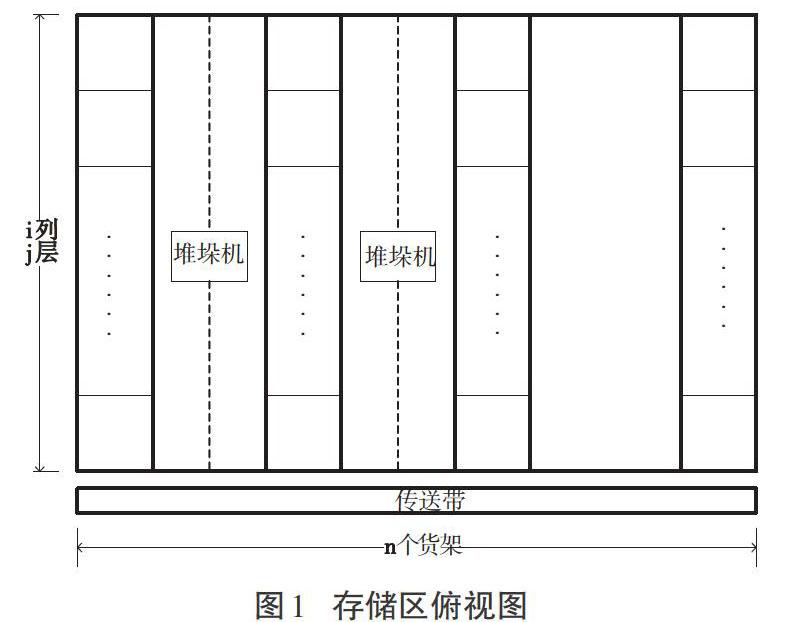
以自动化立体仓库的高位货架为研究对象。设仓储区共有[n]个高位货架，且每个高位货架有[i]列[j]层。选定出入口为零点，即最靠近仓库口的货架为第一个，最靠近传送带的第一竖排货位为第一列，最靠近地面的第一横排货位为第一层。以出入口为原点，建立三维坐标系，其中[X]轴方向为传送带方向，垂直于货架，速度为[Vx];[Y]轴方向为平行货架方向，速度为[Vy];[Z]轴方向为竖直向上方向，速度为[Vz]。存储区平面图如图1所示。

图1 存储区俯视图

此类自动化立体仓库多为标准化包装，在出入库作业时，并不需要考虑货品外观因素。此外，货品出入存储区是其出入库作业最重要的组成部分。因此，评价仓库效益最重要的指标便是出入库效率。

2 模型构建

2.1 基本假设

①货位货品相适应，同一货位货品无混放;②使用一种通用托盘;③堆垛机和传送带在其运动方向上均是匀速运动，仓储区作业均采用同种堆垛机，面对货架正面一侧作业;④单出入库口模式，出入库口在同一侧;⑤货位货格形状为正方体，即长、宽、高相同，且相邻货位紧挨。

2.2 数学模型

通常用单位时间内流转的某类货品的数量来表示货物的周转率[P]，计算公式为：

由于堆垛机在水平和竖直方向上是匀速运动，因此它将货品入库送至指定货位和指定货位取货的耗时一定。如在某一货位[（i，j）]上的周转率为[Pij]，出入库作业总时间为[T]，则该货位单位时间内出入库作业总耗时为：

用[Tijk]表示位于货位[（i，j，k）]处的货品被搬运到出口耗费的时间（单位：s），经分析，可得：

其中，[h]表示相邻两个货位直接的平均距离，m;[f]表示每两个相邻货架之间平均距离，m。

只要知道所有货位上单位时间内的周转率及每个货位对应的单次出入库作业时间，就能知道单位时间内仓储区堆垛机所需要进行出入库作业的总耗时，如式（4）所示：

其中，[Pijk]表示位于货位[（i，j，k）]处货品的周转率，件（台）/月。

将式（3）代入式（4）中，有

本模型约束条件如下：

最终确定货位优化模型如下：

通过分析，由于单个货品只能放入一个货位，且不同货品不能共用一个货位，此类思想类似于0～1整数规划问题中的指派问题，因此可以引入指派问题的思想和方法简化求解过程。得出指派模型为：

其中：

3 案例研究

3.1 选定对象

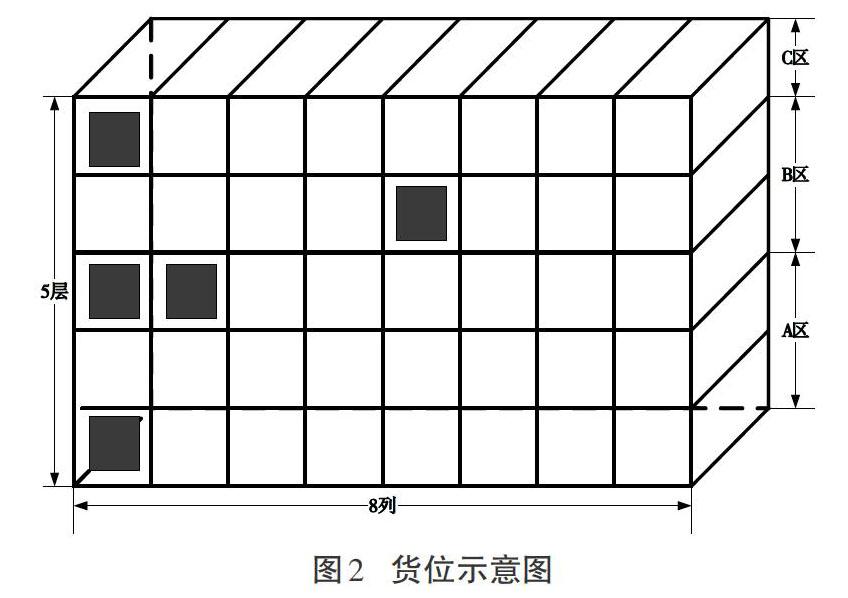
本文随机截取了某仓库休闲食品区的存储货架8列5层共计40个货位进行研究。给选定的货品进行编码：1号货品用[u1]表示，2号货品用[u2]表示，以此类推，[v]号货品用[uv]表示。

假如只研究单一货架时，底层距离出入口更近，因此频次更大货品更应该靠下;假如研究多个货架时，就应该将周转率高的货品放置在靠近出入库口的货架上面。据此将所选的货位分为A、B、C三个区域，分别用于存储周转率高、中和低的货品。选取的货位已存储有货品，其货位固定不变。货位示意图如图2所示。

在此基础上，根据选取的8类货品周转率的差异，将其分类a、b、c三类，分别对应A、B、C存储区，货品分类表如表1所示。

3.2 案例计算

利用公式（2）可以求得每个货品指派到每个货位上的[f]值，即为指派模型的系数，可以得出指派模型的系数矩阵，求得指派方案。部分[f]值如表2所示。

首先得到a类货品分配到A区每个货位的系数值，得到可行分配方案的系数矩阵为：

既而，通过匈牙利法计算得到最终解矩阵为：

同理，得到b类货品分配到B区每个货位的系数值，可行分配方案的系数矩阵为：

计算得到解矩阵为：

同樣，得到c类货品分配到C区每个货位的系数值，可以得到系数矩阵为：

计算得到解矩阵为：

综上，最终得到货位分配方案如图3所示。其中，货物和货位的对应关系如表3所示。

3.3 结果分析

实例计算完成后，可得到货位分配方案如表3所示，既而可求出该策略下的目标函数值为645。

依据原随机存储策略，货品一般依照就近原则先入先放，其存储策略如表4所示，该策略下的目标函数值为739.6。可见，通过本文的优化方法，效率可以提高14.67%。

通过上述分析可知，本文的优化方法能较大幅度地提升货品出入库效率。同时，在有限货位的情景下，本文的货位分配方法相较于以往随机分配方法更易于理解和操作，兼顾了入库和出库的效率。

4 结语

通过对自动化立体仓库性质和业务特征的分析，制定了货品存储策略，构建了基于出入库效率最高的货位优化模型，通过求得的有限个[f]值构成全部可行解矩阵，将货位分配的问题转化为整数规划的指派问题，接着利用匈牙利法得到解矩阵。最后通过实例验证了本文方法的可行性和合理性。

参考文献：

[1] Elisa FM， Cavalcante Cristiano Alexandre Virgínio. Using the Efficient Frontier to Obtain the Best Solution for the Storage Location Assignment Problem[J]. Mathematical Problems in Engineering，2014（10）：1-10.

[2]侯中，郑国华.基于遗传算法的汽车零配件仓库货位优化研究[J].铁道科学与工程学报，2016（11）：2305-2312.

[3]李永伟，刘树安，郭晋秦.普通立体仓库的货位优化模型与算法研究[J].计算机工程与科学，2019（2）：321-327.

[4]高楠，王莲花，李筱烨.基于拣选型立体仓库的货位优化问题研究[J].物流科技，2019（5）：153-157.

[5]徐伟华，沈文喆，巫仁亮，等.基于遗传算法的密集型自动化立体仓库货位分配优化研究[J].物流科技，2019（9）：165-168.

[6] Zhang S ， Fu L ， Chen R ， et al. Optimizing the Cargo Location Assignment of Retail E-Commerce Based on an Artificial Fish Swarm Algorithm[J]. Mathematical Problems in Engineering， 2020（5）：1-14.

[7]郭娟，钱吴永.基于粒子群算法的立体仓库货位优化研究[J].物流科技，2020（4）：156-160.