三峡库区蔡积边坡复杂工况耦合作用的边坡渗流稳定性分析

李险峰

（淮北职业技术学院建筑工程系，安徽淮北235000）

降雨、库水位是导致三峡库区边坡失稳的重要诱因[1-2]，降雨与库水位变动导致了边坡土体的强度降低，因而导致滑坡灾害的发生[3-5]。对于单独降雨条件下或者单独的库水位作用下的边坡渗流稳定性规律，国内外学者进行了许多有益的研究。在单独降雨情况下，叶帅华针对边坡体不同深度处基质吸力随雨水入渗的变化情况，建立了流固耦合计算模型，对降雨入渗条件下黄土高边坡的稳定性进行了分析研究[6]；王保林建立了含软弱夹层的黏性土坡二维有限元计算模型，对降雨入渗下的边坡渗透稳定性进行了数值模拟研究[7]；郭友军对降雨条件下的煤系土边坡渗流特性及边坡安全系数变化规律进行了研究[8]。在单独库水位作用条件下，张祖莲研究了汉江孤山航电枢纽工程区近坝滑坡在不同库水位骤降速率下的渗透稳定性规律[9]；王力研究了库水位骤降情况下的动水压力型滑坡的稳定特性[10]。但是，实际上，降雨发生的持续时间相对较短，而库水位下降的时间相对较长，前人对降雨-库水位联合作用多集中在降雨发生过后库水位下降，或者库水位下降完成过后再进行降雨分析，但是对于降雨发生在库水位骤降时刻的边坡渗流稳定性研究较少。

本文针对以往研究的不足，以三峡库区蔡积边坡为例，对三个典型工况的渗流稳定性规律进行了系统深入的探讨（三个工况是：1）单纯库水位骤降；2）单纯降雨工况；3）库水位降雨耦合工况），以期为三峡库岸边坡的稳定性认识及灾害防护提供一定的参考。

1 计算理论与模型

1.1 计算理论

（1）非饱和计算原理

非饱和渗流微分方程为[11]

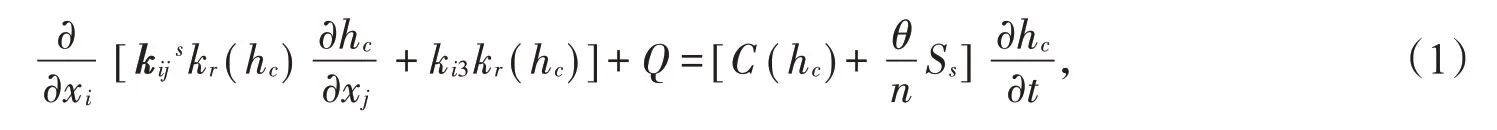
式（1）中，kr是透水率，ksij是渗透张量，hc是水头，Q是源汇，C（hc）是容水度，θ是水头函数，n是孔隙率，Ss是单位贮水量。

（2）非饱和边坡抗滑稳定理论

非饱和边坡抗滑稳定理论如下式所示[11]：

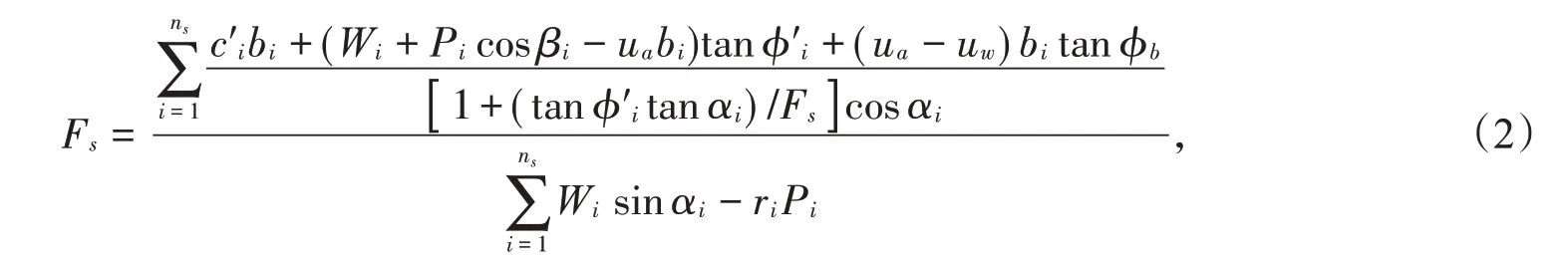
其中，c′i为有效粘聚力，i为土条编号，Wi为质量，Pi为水压力，βi为倾角，ua为孔隙气压力（一般取0），bi为土条宽度，φ′i为内摩擦角，uw为孔隙水压力，φb为基质吸力贡献所对应的摩擦角。

1.2 计算模型

某典型边坡体位于三峡库区，正常蓄水位为175 m，死水位为145 m，对滑坡体所在的网格进行加密处理，整个模型一共划分成1 689个节点、1 632个单元。同时，在滑体内部设置3个监测点（如图1，图2所示）以反映边坡内部不同点的孔压变化规律。

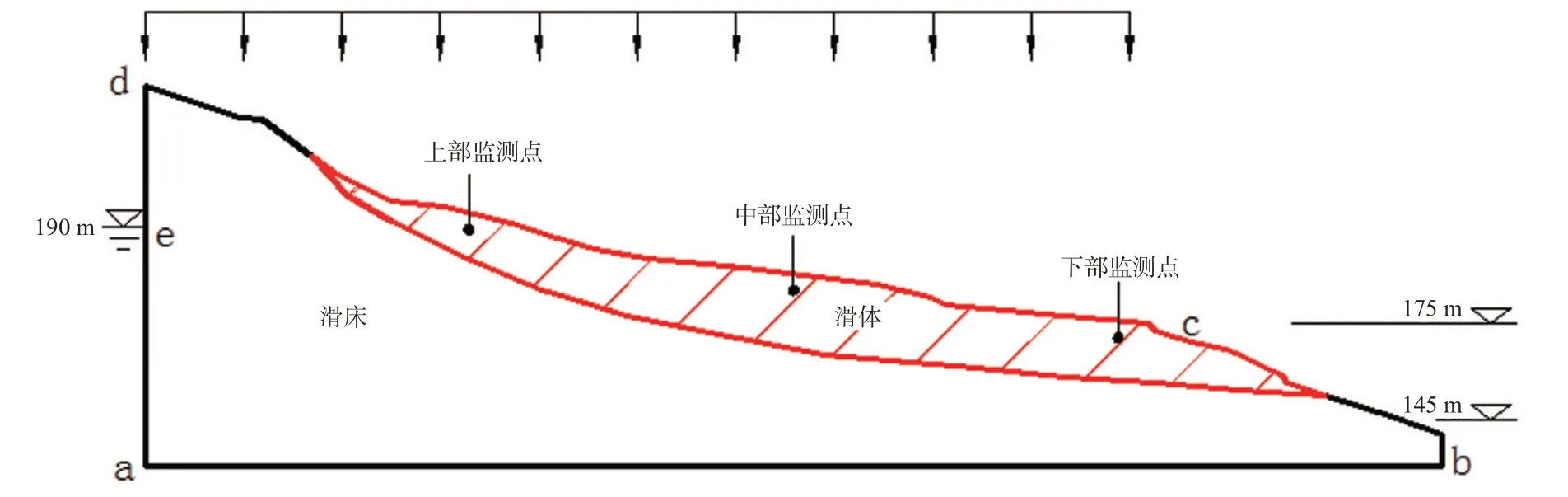
图1 计算模型图

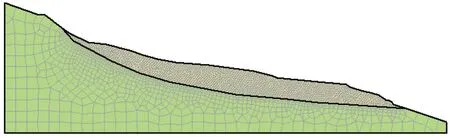
图2 计算模型图网格剖分

2 边界条件及计算参数

模型的初始条件设置如图1所示，以ae为185 m定水位边界，cd为175 m定水位边界计算所得的渗流场作为其他各个库水位联合降雨工况下的初始渗流场。计算参数根据室内试验的实测数据取值，材料力学参数及渗流参数如表1所示。

表1 材料物理力学参数

3 工况设置

以往研究多将降雨与库水位作用分开，或者仅仅将降雨施加在库水位骤降结束时刻进行相应的分析，然而事实上，库水位骤降过程较降雨时长要长，降雨具有随机性，降雨可能发生在库水位骤降的不同时刻，因此，根据三峡库区多年收集的水文资料，确定3个等级的降雨，即大雨（降雨强度为0.05 m·d-1），暴雨（降雨强度为0.1 m·d-1）及特大暴雨（降雨强度为0.2 m·d-1），降雨的平均时长取2 d。根据三峡库区多年运行情况，取库水位骤降速率分别为0.5 m·d-1、1 m·d-1与1.5 m·d-1。具体工况如表2所示。

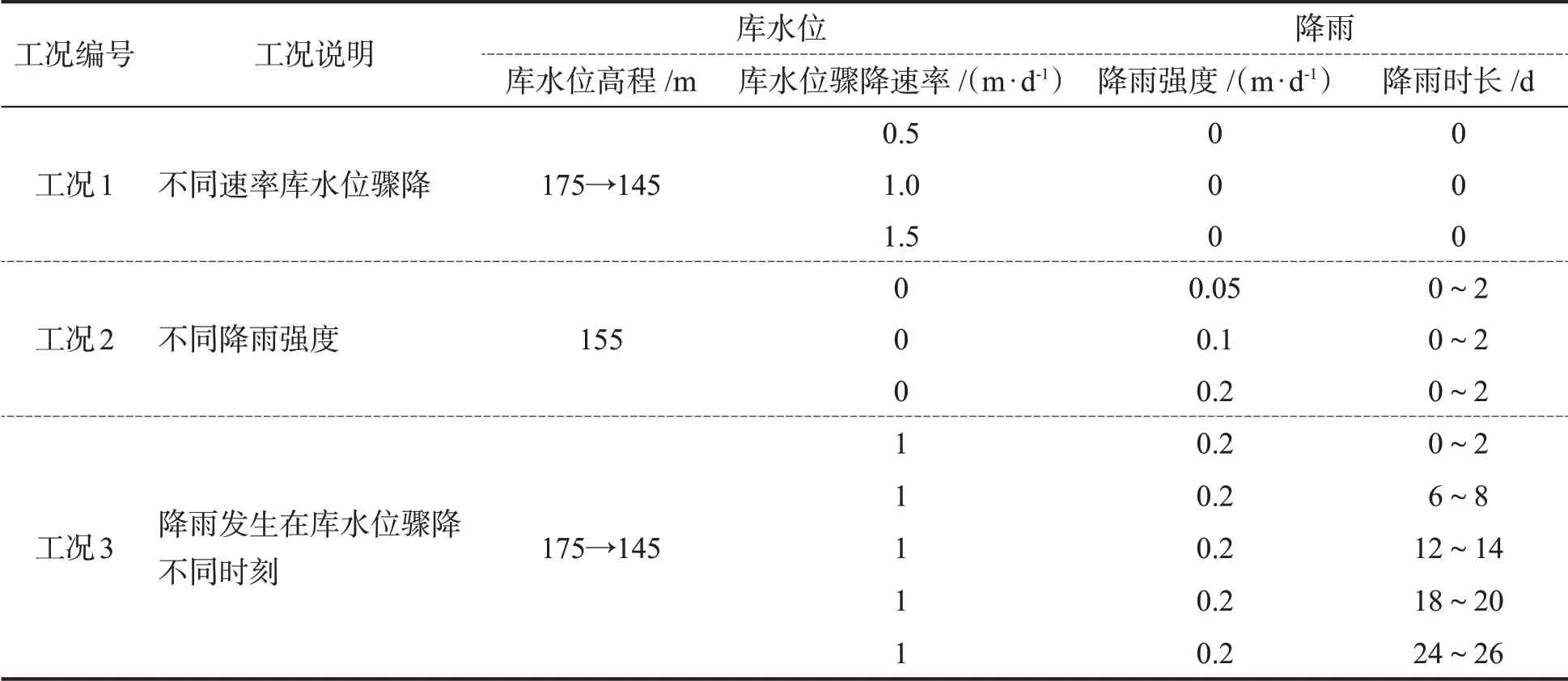
表2 计算工况

4 结果分析

4.1 不同速率库水位骤降工况

工况1下不同监测点的孔压变化规律如图3所示。

由图3可见，库水位骤降情况下边坡内部水压持续下降。位于边坡上部的监测点（如图3（a）），不同库水位骤降速率下不同工况的孔压差异很小，而位于边坡下部的监测点（如图3（c））不同工况的孔压差异较边坡上部的监测点要大。库水位的下降速率越大，孔压的下降速率也越大。位于边坡下部的孔压整体上要大于上部监测点的孔压。

工况1 的安全系数变化如图4 所示。库水位骤降工况安全系数是先降后升，不同库水位骤降速率0.5 m·d-1、1 m·d-1及1.5 m·d-1情况下的安全系数最大降幅分别为5.3%、6.4%与7.1%。

4.2 不同降雨强度工况

工况2不同监测点的孔压变化如图5所示，安全系数变化规律如图6所示。

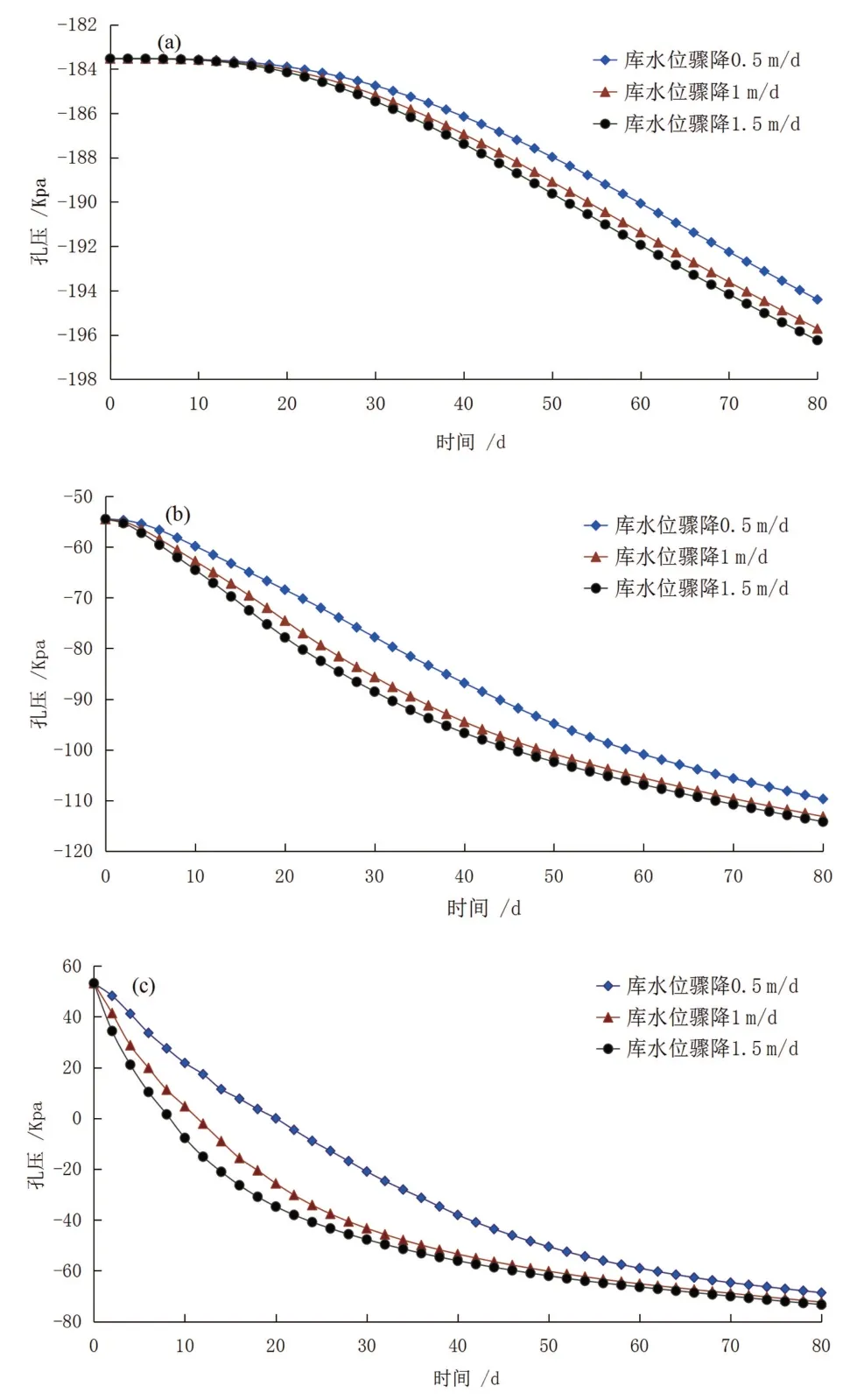
图3 工况1孔压变化规律。

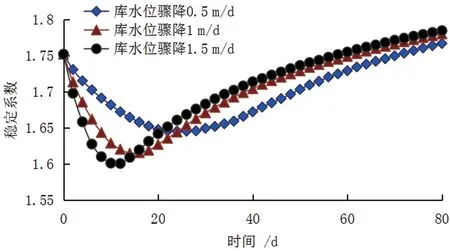
图4 工况1安全系数变化

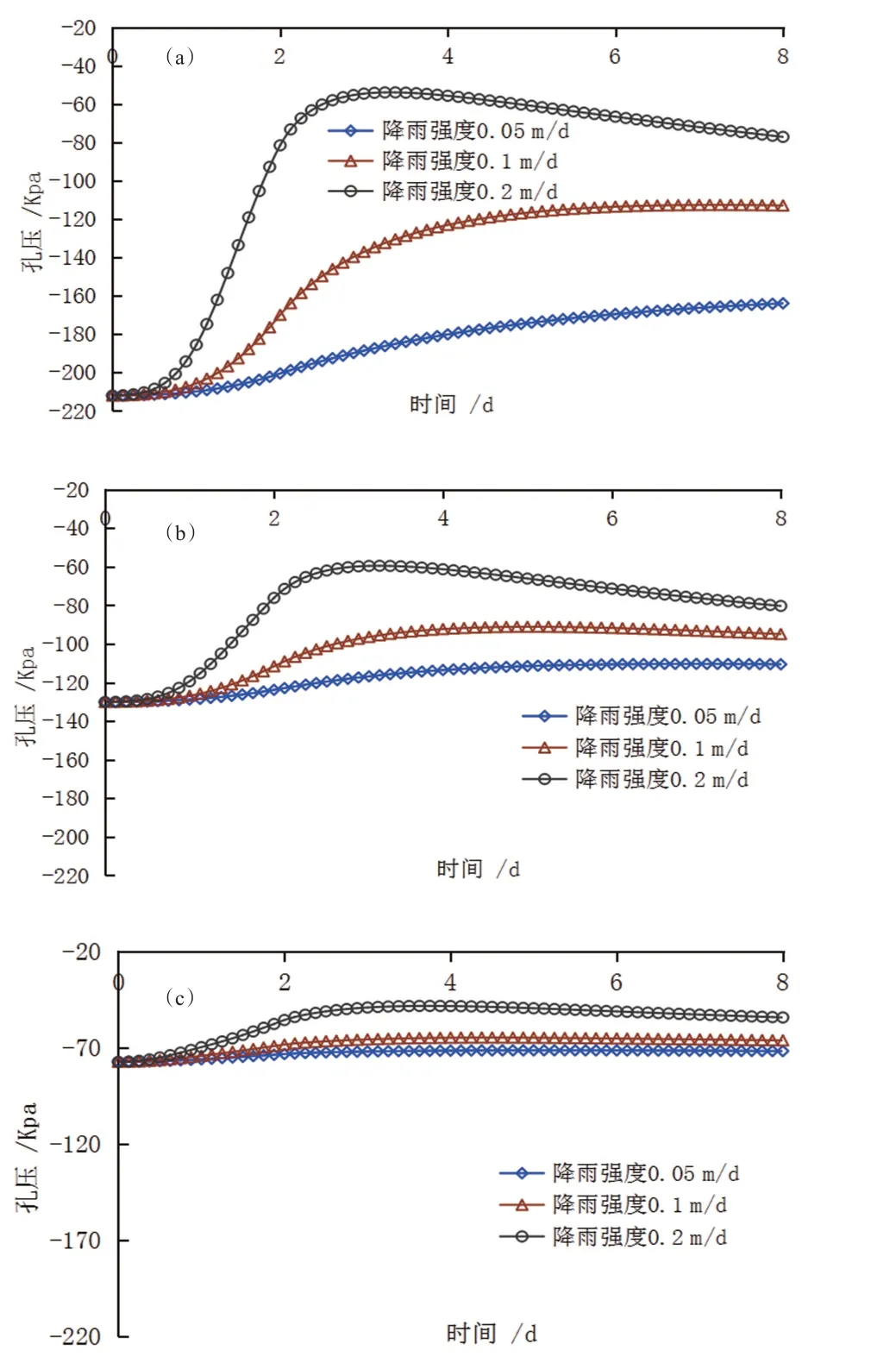
图5 工况2孔压变化规律。

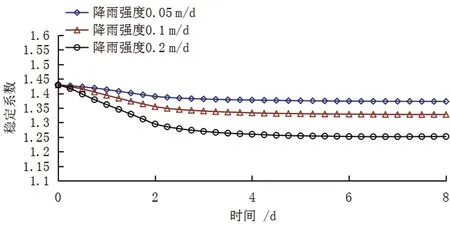
图6 工况2安全系数变化

对于不同降雨强度而言，其孔压变幅要明显大于库水位骤降情况，可见降雨对边坡内部含水率变化的影响要远大于库水位骤降的影响。降雨情况下边坡内部孔压经历一个先增大、后稳定的过程，且降雨强度越大，孔压的升幅越大。与工况1 相同，位于下部点的孔压整体上要高于上部点的孔压。

降雨工况指在降雨时刻骤降而后维持稳定。由图6 可得，不同降雨强度情况下，降雨强度分别为0.05 m·d-1、0.1 m·d-1和0.2 m·d-1时，安全系数的最大降幅分别为6.3%、7.5%及8.8%，可见降雨对安全系数的变幅影响要大于库水位骤降因素；库水位骤降的最小安全系数也要大于降雨情况，但是，最小安全系数都处于1.25 以上，根据水利工程相应规范[12]可以认为边坡基本处于稳定状态。

4.3 降雨发生在库水位骤降不同时刻

工况3 的孔压变化如图7 所示。降雨发生在库水位骤降的不同时刻情况，孔压变化则是综合了库水位骤降及降雨的综合特性，即孔压整体上呈下降的规律。但是在降雨时刻，由于降雨的原因，孔压在该时刻有个突升的过程，整个孔压变化呈一个单锋的规律。值得注意的是，位于边坡上部的点，库水位骤降导致的孔压变幅小，降雨导致的孔压变幅大；位于边坡下部的点，库水位骤降导致的孔压变幅大，降雨导致的孔压变幅则相对较小。

工况3 的安全系数变化如图8 所示。降雨发生在库水位骤降的不同时刻，规律则有所不同。降雨发生在0～2 d、6～8 d、12～14 d、18～20 d 和24～26 d 情况下，安全系数的最大降幅分别为13.8%、16.3%、14.2%、12.6%和10.7%，可见此工况下安全系数的最大降幅都要大于单纯库水位骤降或者是降雨情况；最小安全系数均小于1.25，根据水利工程相应规范[12]，此时边坡安全稳定具有较大的风险。由此可以看出，降雨联合库水位是滑坡产生失稳的重要原因。值得注意的是，降雨发生在库水位骤降不同时刻下的最小安全系数也不一样，降雨发生在第6～8 d时最小安全系数最小。与以往研究仅仅把降雨施加在库水位骤降结束时刻待果不同，本研究发现，降雨发生在库水位骤降过程中出现最小安全系数。

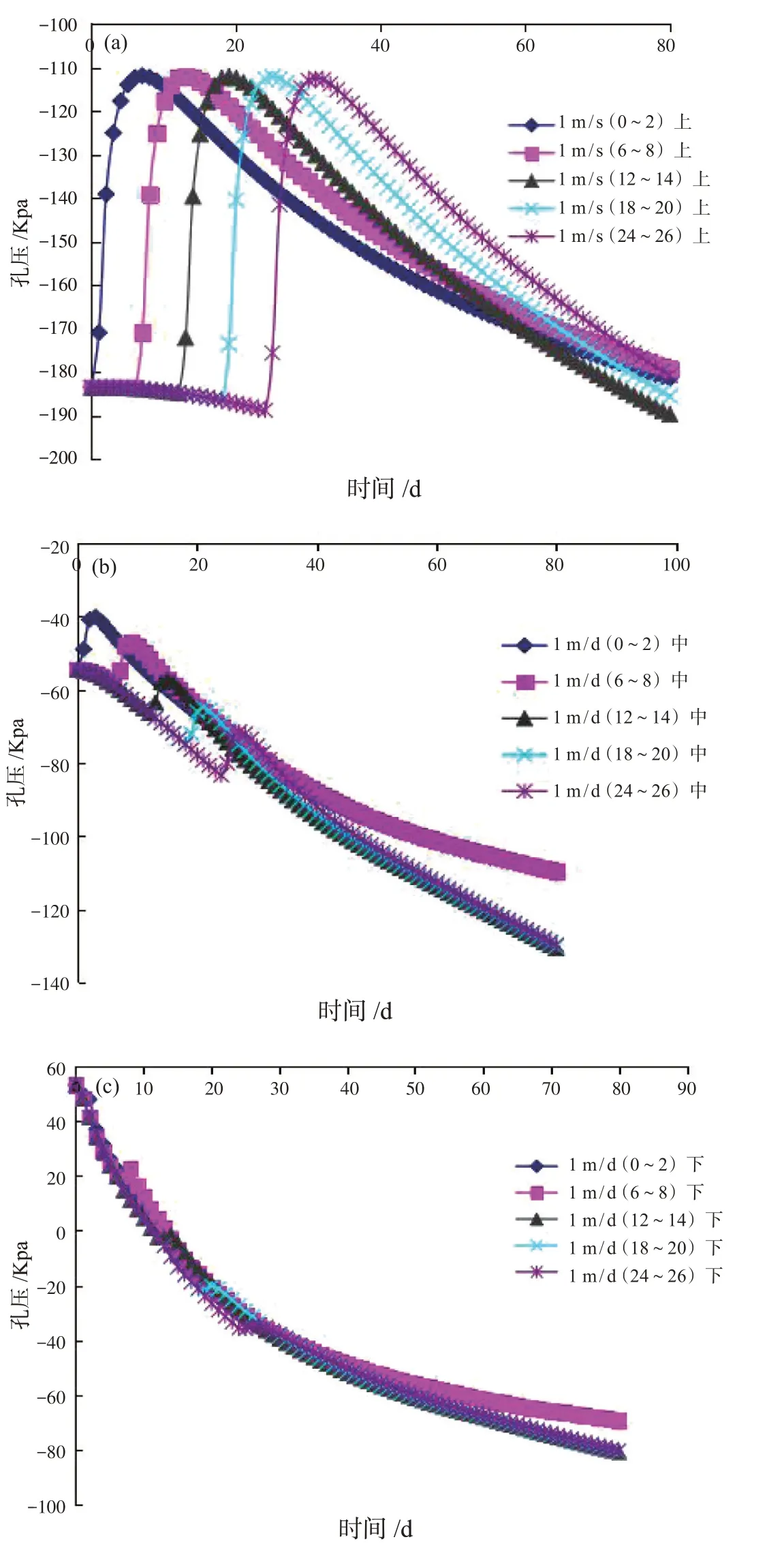
图7 工况3孔压变化规律。

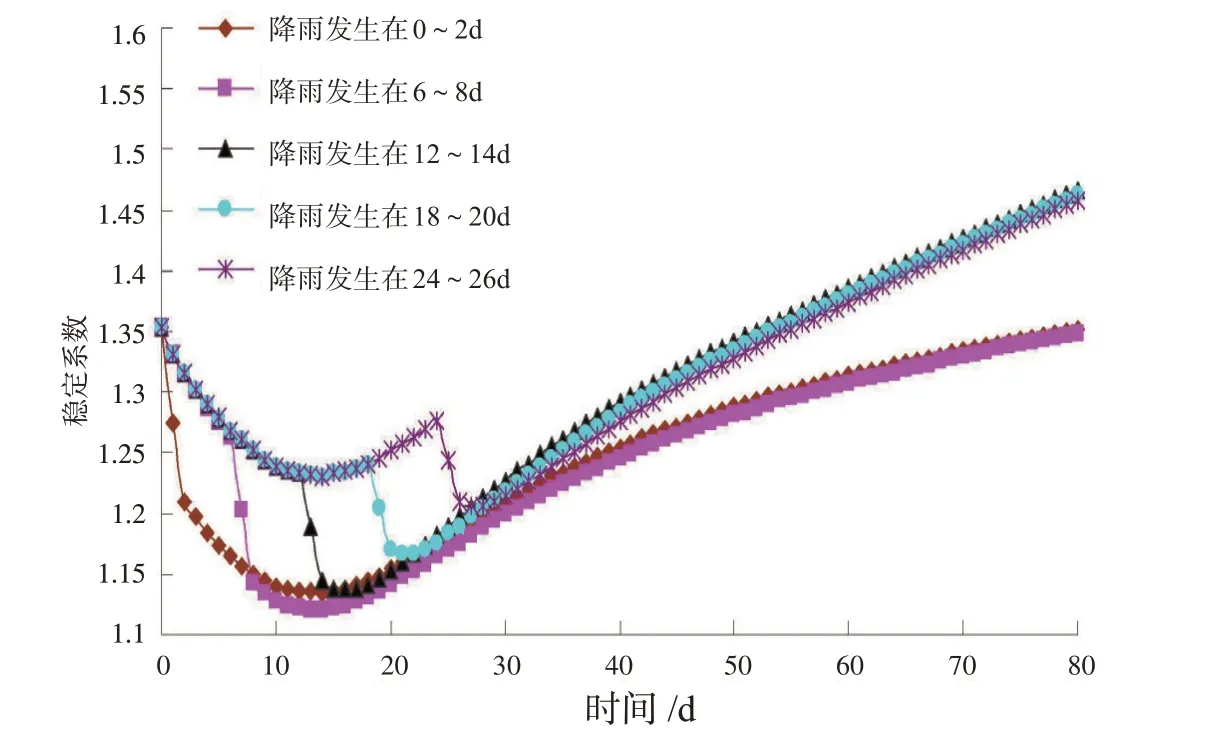
图8 工况3安全系数变化

5 结 论

综上所述，（1）库水位骤降速率与孔压下降呈正相关，降雨强度与孔压上升幅度呈正相关，单纯降雨孔压上升幅度要大于库水位情况孔压下降幅度，降雨发生在库水位骤降时刻的孔压变化特性综合了降雨情况与库水位情况，位于边坡下部的孔压值要大于上部的孔压值。（2）在静库水位工况下，降雨强度越大，降雨时间历时越长，滑坡体内部孔压上升幅度越大；滑体下部孔压值总体要大于滑体中上部，库水位水平越高，降雨强度越大，降雨时长越长，安全系数越小。（3）在库水位骤降与不同时刻降雨联合作用下，滑体最危险情况并非出现在库水位骤降开始联合降雨、或者库水位下降结束时联合降雨的时候，而是出现在库水位骤降过程中联合降雨。因此，在三峡库区边坡稳定性研究中必须考虑降雨-库水位耦合情况，且需要对降雨发生在库水位骤降的不同时刻进行密切监测。