明辨概率与频率

领 衔 人：崔恒刘

组稿团队：江苏省初中数学学科课程示范基地（东台市实验中学教育集团）

文 季承洁

概率与频率是两个不同的概念，它们既有区别又有联系。事件发生的概率是一个确定的数值，而频率是不确定的数值。我们可以通过试验，用频率估计概率的大小。在试验次数较少时，频率的大小不够稳定，不能反映概率，但当试验次数渐渐增多时，频率会逐渐稳定在概率附近，而且非常接近概率，但不一定相等。我们可以利用频率的稳定性估计相应的概率，也可以利用概率来预测不确定事件进行多次试验后的频率，由此解决实际问题。

一、概念辨析

例1 做“抛掷一枚质地均匀的硬币”试验，在大量重复试验中，对于事件“正面朝上”的频率和概率，下列说法正确的是（ ）。

A.概率等于频率

C.概率是随机的

D.频率会在某一个常数附近摆动

【解析】频率只能估计概率，不一定等于概率，故A选项错误；频率是试验的统计结果，是随机的，它随试验而变化，是一个不确定的值，故B选项错误；事件发生的概率是唯一确定的一个值，抛掷一枚质地均匀的硬币，正面朝上的概率等于故 C 选项错误；当试验次数很大时，频率稳定在概率附近，故D选项正确。

【点评】本题考查概率与频率的概念辨析，我们需要正确理解概率与频率的概念和关系：反复试验时，某事件发生的频率会稳定在某个常数的附近，这个常数就叫作事件概率的估计值，而不是一种必然的结果。

二、通过模拟试验来估计概率

例2 （2020·新疆）下表中记录了某种苹果树苗在一定条件下移植成活的情况：

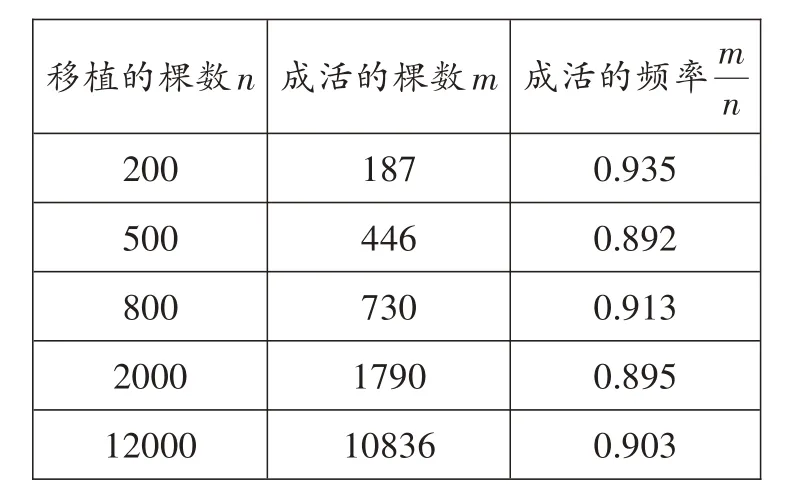
0.935 0.892______________________________0.913 0.895 0.903移植的棵数n 200__________500__________800_________2000________12000_______成活的棵数m 187 446 730__________________1790 10836成活的频率m_____________________________________n

由此估计这种苹果树苗移植成活的概率约为_______。（精确到0.1）

【解析】由表格可知，试验次数为12000（足够多）时，它的频率为0.903≈0.9，所以估计这种苹果树苗移植成活的概率约为0.9。

【点评】本题考查利用频率估计概率：在一定条件下，试验次数足够多时，随机事件发生的频率会在某个常数附近摆动，这个常数就是频率的稳定值。频率的稳定值就作为这个随机事件发生的概率的估计值。

三、掷瓶盖试验判断结论

例3 下图显示了小亚用计算机模拟随机投掷一枚某品牌啤酒瓶盖的试验结果。

那么可以推断出如果小亚实际投掷一枚这个品牌的啤酒瓶盖时，“凸面向上”的可能性_______“凹面向上”的可能性。（填“大于”“等于”或“小于”）

【解析】根据图中数据可得，“凸面向上”的频率在 0.443 与 0.440 之间，所以“凸面向上”的可能性小于“凹面向上”的可能性。

【点评】本题考查了利用频率估计概率。解答本题的关键是明确概率的定义，利用数形结合的思想，根据图中的数据解答。

四、通过模拟试验来估计能发芽的作物种子数量

例4 某农科所在相同条件下做玉米种子发芽试验，结果如下：

某位顾客购进这种玉米种子10千克，那么大约有_______千克种子能发芽。

【解析】根据农科所在相同条件下做玉米种子发芽率的试验结果，可以发现经过大量重复试验后，玉米种子发芽的频率稳定在0.88左右，由此求出10千克种子中能发芽的种子的质量是：10×0.88=8.8（千克）。

【点评】此题主要考查了利用频率估计概率，大量反复试验下，频率稳定值即概率。解答此题的关键是判断出大量重复试验后，玉米种子发芽的频率稳定在0.88左右。