课本中摸球概率题的演变史

2020-12-05柳宏明

初中生世界 2020年43期

关键词：红球红红小球

文柳宏明

教材是中考命题的天然素材，每年都有大量的中考题目直接出自教材，或撷此作基，演变生发。我们以苏科版数学教材九年级上册第136页例4为源，探其演、究其变。

【原题再现】一只不透明的袋子中装有1个白球和2 个红球，这些球除颜色外都相同。搅匀后从中任意摸出1 个球，记录颜色后放回、搅匀，再从中任意摸出1 个球。求两次都摸到红球的概率。

中考演变1：摸一次

例1 （2020·黑龙江哈尔滨）一个不透明的袋子中装有9 个小球，其中6 个红球、3个绿球，这些小球除颜色外无其他差别。从袋子中随机摸出一个小球，则摸出的小球是红球的概率是（）。

【分析】将原题中的摸2次弱化为摸1次，直接考查一步事件概率。根据随机事件概率大小的求法，找准两点：①符合条件的情况数目，②全部情况的总数。二者的比值就是其发生的概率的大小。

解：∵袋子中一共有9 个除颜色不同外其它均相同的小球，其中红球有6个，

【点评】本题主要考查概率公式，解题的关键是掌握随机事件A 的概率P（A）=事件A可能出现的结果数÷所有等可能出现的结果数。

中考演变2：摸两次，从两个袋子中各摸一个球

例2 （2020·黑龙江鹤岗）现有两个不透明的袋子，一个装有2个红球，1个白球，另一个装有1 个黄球，2 个红球，这些球除颜色外完全相同。从两个袋子中各随机摸出1 个球，摸出的两个球颜色相同的概率是（）。

【分析】将原题中的“摸一次、放回、再摸一次”演变为“分别从两个袋子中各摸一个球”，两者摸法上有区别，但模型是一样的。用列表法列举出所有等可能出现的结果，从中找出“两球颜色相同”的结果数，进而求出概率。

解：用列表法表示所有等可能出现的结果情况如下：

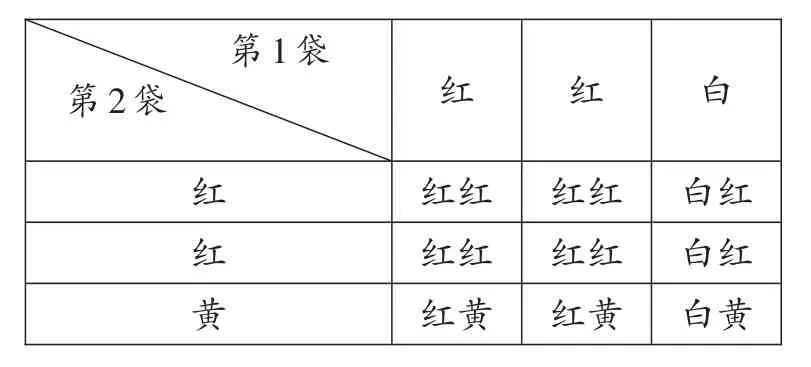
第1袋第2袋红红白________________________红________________________红_____________________黄红红__红红__红黄__红红__红红__红黄__白红_白红_白黄_

共有9 种等可能出现的结果，其中“两球颜色相同”的有4种，

【点评】将教材的原题换一种叙述方式考查，形异实同，考查同学们对基础知识的掌握情况。这也是最基本的命题方式。

中考演变3：摸两次，不放回

例3 （2020·黑龙江牡丹江）在一个不透明的口袋中有四个完全相同的小球，把它们分别标号为1、2、3、4。若随机摸出一个小球后不放回，再随机摸出一个小球，则两次取出小球标号的和等于5的概率为（）。

【分析】将原题中的“摸一次、放回、再摸一次”演变为“摸一次、不放回、再摸一次”。不放回，摸出的球将不会被摸到，这是列出所有等可能出现的结果时需要注意的地方。

解：用列表法表示所有等可能出现的结果情况如下：

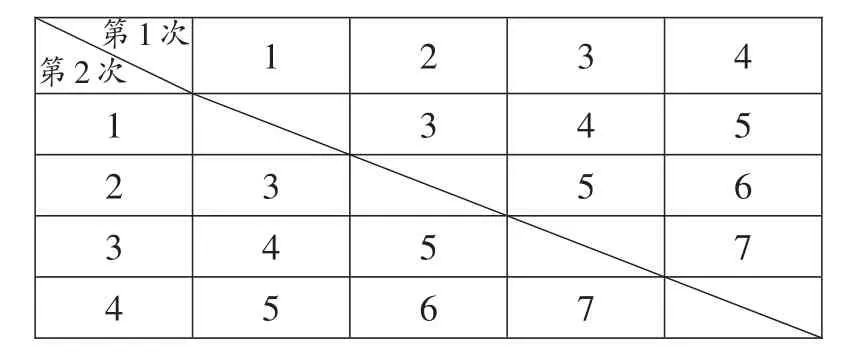
第1次第2次4_______________________________________5______________________________________6_______________________________________7 1________________2_______3___________________4 1_______ 3_______________4_______5_______2_______ 3________5____________________6_______3 4____________5____________7____________

共有12 种等可能出现的结果，其中“和等于 5”的有4 种，故选C。

【点评】对于袋中球摸两次，同学们需要看清题目条件的叙述是“有放回”还是“无放回”。对于从不透明的袋中一次摸出两个球，则相当于“摸一次、不放回、再摸一次”，换个背景如“掷骰子、抛硬币、摇转盘”两次，第一次出现的，第二次还有可能出现，相当于“摸一次、放回、再摸一次”。