考虑弱透水层的单井注抽试验解析模型研究
2020-12-04刘玉舒戴炆君王全荣
刘玉舒,戴炆君,刘 洋,王全荣
(1.中国地质大学(武汉) 环境学院,湖北 武汉 430074;2.山东省地质科学研究院,山东 济南 250013)
单井注抽(Single-Well Push-Pull,SWPP)试验是在同一口井内进行注入和抽取示踪剂,通过拟合获取的井筒内溶质穿透曲线,从而获取含水层物理化学参数的一种试验方法[1-3]。由于SWPP试验具有操作简单、耗时短和成本低等优点,从而被广泛用于获取含水层的弥散度、孔隙度、吸附解析系数等参数[4]。到目前为止,国内外学者开展了大量的理论模型研究[5-6]。如Gelhar等[7]、Schroth等[8]和Wang等[9]推导了不同条件下SWPP试验的解析解,被广泛用于获取含水层的纵向弥散度;Humphrey等[10]、Harvey等[11]和Snodgrass等[12]建立了考虑一阶化学反应的SWPP试验数学模型。
但是,上述研究均忽略了弱透水层对SWPP试验结果的影响。实际的含水层系统通常是由透水性相对强的含水层和透水性相对弱的弱透水层构成。弱透水层一般是由黏土或淤泥组成的低渗透性介质,吸附性强,对溶质运移过程起着至关重要的作用。Zhan等[13]和Wang等[14]建立了考虑弱透水层的溶质运移模型,并指出弱透水层分子扩散作用对含水层中溶质迁移产生的影响不可忽略。为此,本文在前人研究的基础上,将弱透水层效应考虑到SWPP试验中,建立了含水层-弱透水层系统中考虑混合效应的 SWPP 试验数学模型,且在含水层-弱透水层系统中考虑了弱透水层的分子扩散作用,采用拉普拉斯变换和格林函数法获得模型的半解析解,并通过与前人的解析解模型进行对比,以验证本模型的可靠性。
1 含水层-弱透水层系统中SWPP试验数学模型的建立
为了简化数学模型,本文做出如下假设:①溶质为反应性溶质,考虑一阶化学反应;②含水层-弱透水层系统中,假定含水层位于上、下两个弱透水层之间,含水层是水平均质等厚的,侧向无限延伸;③注抽试验中的井是一口完整井,井半径为rw。建立的含水层-弱透水层系统中SWPP试验的数学模型如下:
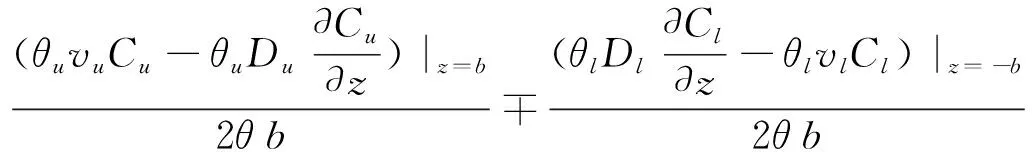
(1)
(2a)
(2b)
C(r,t)|t=0=Cu(r,z,t)|t=0=Cl(r,z,t)|t=0
(3)
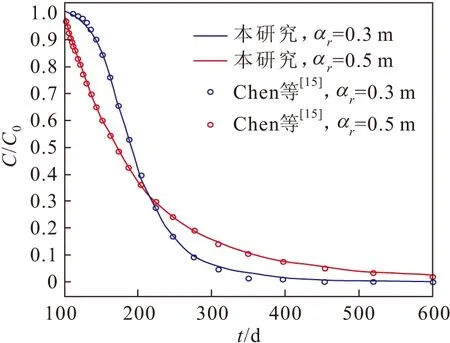
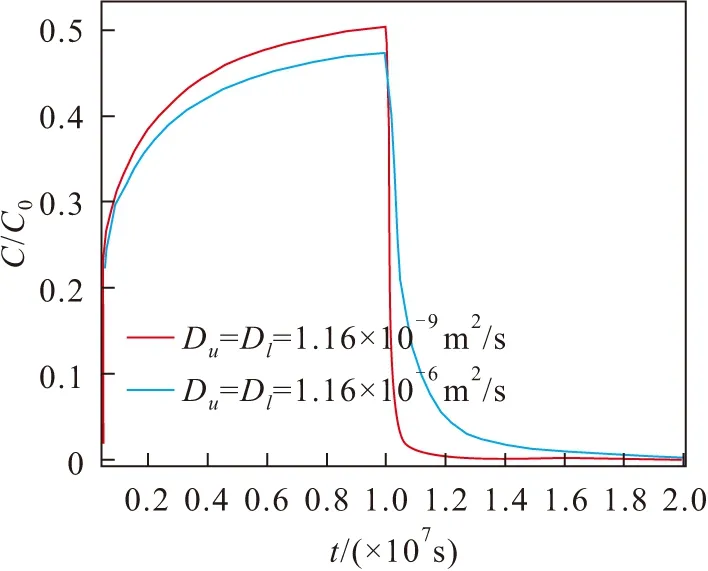
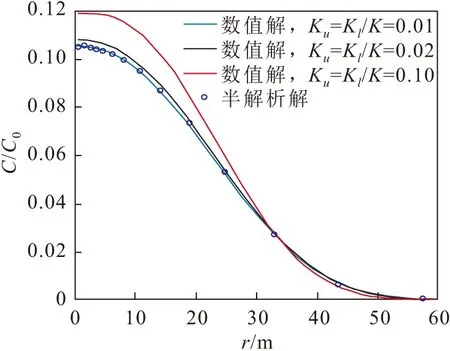
(0 (4a) (0 (4b) (0 (5a) Cinj(t)|t=0=0 (rw≤r≤re) (5b) (6a) Cext(t)|t=tinj=Cinj(t)|t=inj(rw≤r≤re) (6b) C(r,t)|r→∞=Cu(r,t)|z→∞=Cl(r,t)|z→-∞=0 (7) Cu(r,z=b,t)=C(r,t) (8) Cl(r,z=-b,t)=C(r,t) (9) (10a) (10b) (10c) (10d) (10e) (10f) 式中:s为拉普拉斯变量;Ctinj为注入阶段结束时刻溶质浓度。 在注入阶段,采用艾里函数推导解析解,弱透水层中溶质运移控制方程(10c)和(10e)的通解如下: (11a) (11b) 将弱透水层中溶质运移的通解(11a)和(11b)代入到(10a)中,可以得到含水层中溶质运移的控制方程如下: (12) 含水层中溶质运移控制方程(12)的通解如下: (13) 将含水层中溶质运移控制方程的通解(13)代入到边界条件(7)、(8)、(9)中,可以得到:b0=0, 故可以得到注入溶质阶段含水层-弱透水层系统中的拉普拉斯域的解为 (14) (15) (16) 在抽取阶段,采用格林函数法推导解析解,上层弱透水层中溶质运移的通解如下: (17) s)(A0,u,ext+B0,u,extZD);A0,u,ext=-B0,u,ext×ZD|ZD→∞; 0;C4,u,ext=[1-exp(a2,ext-a1,ext+a1,extZD-a2,extZD)]C2,u,ext. 在抽取阶段,下层弱透水层中溶质运移的通解如下: (18) 可以得到含水层中溶质运移的控制方程如下: (19) 边界条件如下: (20) 在抽取阶段,含水层中溶质运移的解析解为 (21) 上述推导得到了含水层及弱透水层中溶质运移在拉普拉斯域的解析解,该解包含艾里函数、格林函数等特殊函数,很难利用解析逆变换的方法进行求解。因此,本文采用数值逆变换的方法来获得实空间下的径向溶质迁移的解,即利用Stehfest数值逆变换方法得到溶质迁移在实空间的解。 本研究的半解析解是Chen等[15]的半解析解的拓展,考虑了井筒内的混合效应和弱透水层的影响。为了检验本模型的可靠性,将本模型的一个特解与Chen等[15]的半解析解进行了比较。在本模型中,将hw-inj设置为0,表示本模型将不考虑混合效应;将弱透水层中的分子扩散系数设置为0,表示忽略弱透水层的影响,因此本模型的半解析解将与Chen等的半解析解相同。本模型参数设置如下:rw=0.2 m,re=100 m,αr=0.3 m,R=1,μ=10-6m-1,θ=0.2,B=10 m,tinj=100 d,Qinj=2.5 m3/d,text=500 d,Qext=2.5 m3/d。图1为本研究与Chen等[15]解析解的溶质穿透曲线对比。 图1 本研究与Chen等[15]解析解的溶质穿透曲线 对比Fig.1 Comparison between the Breakthrough Curves (BTCs) computed by analytical solution of this study and Chen et al.[15] 由图1可见,本研究与Chen等[15]解析解的结果很好地吻合,说明本文建立的含水层-弱透水层系统中SWPP试验的数学模型是可靠的。 图2 弱透水层分子扩散系数对井筒内溶质穿透 曲线的影响Fig.2 Influence of molecular diffusion coefficient of aquitard on BTCs at well screen 图2为弱透水层分子扩散系数对井筒内溶质穿透曲线的影响。图中的两条曲线分别表示整个单井注抽阶段是否考虑弱透水层分子扩散作用情况下井筒内溶质的穿透曲线。模型参数设置为:rw=0.2 m,re=600 m,αr=2 m,θm=θu=θl=0.36,B=4 m,tinj=1×107s,text=1×107s,Qinj=2.09×10-6m3/s,Qext=2.09×10-6m3/s,Du=Dl=1.16×10-6m2/s。其中αr的取值与Zhan等[13]的研究一致。当上、下弱透水层的分子扩散系数Du=Dl=1.16×10-9m2/s时,可以视为不考虑弱透水层分子扩散作用的情况。 由图2可见,在注入阶段,当考虑弱透水层分子扩散作用的影响时,从含水层向弱透水层中发生扩散的溶液越多,因此溶质穿透曲线越低;在抽取阶段前期,因为考虑含水层溶质向弱透水层中的分子扩散作用,含水层中存留的溶质浓度越低,因此抽取阶段早期溶质穿透曲线越低;而在抽取阶段后期,因为水流的反向抽取,也会有溶质从弱透水层向含水层发生反向扩散,因此抽取阶段后期溶质穿透曲线越高。 在含水层-弱透水层系统中,弱透水层对含水层中溶质迁移的影响也是不可忽略的,为了研究本文模型的适用性,采用有限元软件COMSOL Multiphysics建立了含水层-弱透水层系统中SWPP试验数值解模型来模拟实际情况下含水层-弱透水层系统中的溶质运移情况,并分析弱透水层渗透系数与含水层渗透系数的不同比值情况下SWPP试验半解析解模型的适用性。设置弱透水层渗透系数与含水层渗透系数的比值分别为0.01、0.02和0.1,其他模型参数设置为:re=100 m,rw=0.5 m,αr=2.5 m,R=1,μ=10-7m-1,θ=0.3,B=10 m,tinj=250 d,Qinj=m3/d,text=250 d,Qext=50 m3/d。在实际情况中,弱透水层渗透系数与含水层渗透系数的比值远小于0.1[16],这里采用渗透系数比值为0.1的情况是为了与真实较小的渗透系数比值情况做对照。图3为t=500 d时不同的弱透水层与含水层渗透系数比值情况下数值解与半解析解的对比。 图3 t=500 d时不同的弱透水层与含水层渗透系数 比值情况下数值解与半解析解的对比Fig.3 Comparison between numerical and semi- analytical solutions at different conductivity ratios of the aquitard and aquifer when t=500 d 由图3可见,当弱透水层渗透系数与含水层渗透系数的比值越接近0.01时,半解析解模型与数值解模型井筒中溶质浓度变化的BTC曲线拟合得越好,也就是说在此比值范围附近半解析解模型的适用性越好,误差可以忽略,精度可满足实际工程需求。这是因为弱透水层的渗透系数比含水层的渗透系数要小得多,所以此模型中只考虑含水层中径向水流与弱透水层中垂向水流[17],即数值解在渗透系数比值更小的情况下与半解析解的拟合度更好。 本文主要研究了单井注抽(SWPP)试验中弱透水层对SWPP试验中溶质径向弥散的影响,采用拉普拉斯变换和格林函数得到模型的半解析解,并通过与Chen等[15]的半解析解进行比较,验证了此模型的准确性,得到如下结论: (1) 弱透水层的分子扩散系数对溶质运移同样具有影响,当考虑弱透水层的扩散作用时,含水层注入阶段和抽取阶段早期的井筒内溶质穿透曲线越低,而抽取阶段晚期的井筒内溶质穿透曲线越高。 (2) 通过与数值模拟结果进行对比,结果表明:弱透水层渗透系数与含水层渗透系数的比值越接近0.01时,半解析解模型与数值解模型井筒中溶质浓度变化的BTC曲线拟合得越好,也就是说在此比值范围附近半解析解模型的适用性越好,误差可以忽略,精度符合实际工程需求。此半解析解模型在弱透水层渗透系数与含水层渗透系数差异较大时适用,在弱透水层渗透系数与含水层渗透系数的比值接近0.01时适用性最好。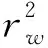
2 数学模型解析解的推导

2.1 注入阶段解析解的推导
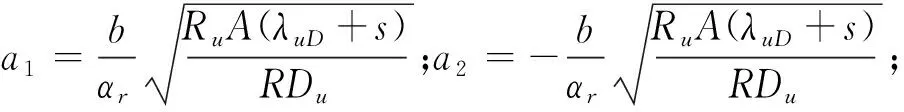
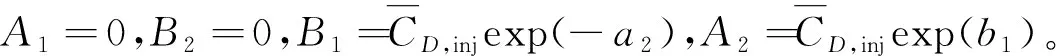


2.2 抽取阶段解析解的推导






3 模型的验证
4 讨 论
4.1 弱透水层溶质扩散作用对含水层中溶质运移的影响
4.2 渗透系数对SWPP试验半解析解模型的影响
5 结 论
