一类指数和的代数次数

陈 超,彭国华

(1.中山大学数据科学与计算机学院； 广州 510006； 2.四川大学数学学院,成都 610064)

1 引 言

设p为奇素数,q=pr,ζp为一个p次本原单位根. 以Tr记从有限域Fq到Fp的迹映射,即Tr(x)=x+xp+…+xpr-1. 本文讨论有限域Fq上形如

的指数和,其中f(x)∈Fq[x]. 这类指数和不只有理论价值,在编码学[1-2]和密码学[3-5]方面也有重要应用.

由如上的指数和可得到分圆域Q(ζp)中一个代数整数. 之前，对它们的研究主要集中在指数和的p-adic性质和|*|∞性质[6-9].最近，以Wan[10]为代表的一些学者研究了这些代数整数的次数,即在Q上添加指数和作为代数单扩张,其扩张次数[Q(Sq(f)):Q]的大小记为degSq(f)=[Q(Sq(f)):Q]. 对于一般的多项式f(x)∈Fq[x],要估计degSq(f)或得到degSq(f)的精确取值是非常困难的.

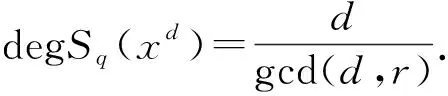
本文基于Wan的结果讨论了r=2,p≡1(mod 4)的情形,得到：若d|(p+1),则Sq(xd)仅有两种可能取值(定理2.2,推论2.4). 在此基础上,我们拓展了Myerson 提出的方法,得到某些情形下Sq(xd)代数次数的精确值(定理3.5),推广了Wan的部分结论.

2 高斯和

对于代数数α,定义α的代数次数为degα=[Q(α):Q],即在Q上添加α所得代数数域的扩张次数.本文主要考虑高斯和Sq(xd)的代数次数,即degSq(xd)=[Q(Sq(xd)):Q]的大小.

若d=1,利用Tr的满同态性质可得

当d=2时,高斯已得到

再由Hasse-Davenport 定理可知

(1)

故

最近,Wan[10]利用Galois理论得到如下结果.

定理2.2若d|(p+1),则Sp2(xd)=-p或(d-1)p.

为了证明定理2.2,我们需要如下引理.

引理2.3[12]设χ为Fq一个非平凡的加法特征,n为正整数,e=gcd(n,q-1). 对任意的a,b∈Fq,a≠0,有

定理2.2的证明 对k=0,1,…,p-1,令

Nk=|{x∈Fp2|Tr(xd)≡k(modp)}|.

则

Sp2(xd)=N0-N1

(2)

又

p2=N0+N1+…+Np-1

(3)

故

Sp2(xd)=mp

(4)

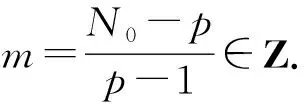
-p≤Sp2(xd)≤(d-1)p.

于是-1≤m≤d-1.因而m=-1或者m=d-1. 所以Sp2(xd)=-p或Sp2(xd)=(d-1)p. 证毕.

对于一些特殊情况,我们还可以得到Sp2(xd)的精确值.

推论2.4设p≡1(mod 4). 若2|d|(p+1),则Sp2(xd)=-p.

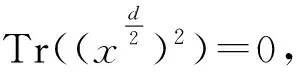
3 高斯和的代数次数

为方便讨论,我们引入一些记号.

对于k=0,1,…,d-1,定义

考虑Gal(Q(ζp)/Q)在φd(x)上的作用便知φd(x)∈Z[x]. 利用Sq(xd)的定义即得Sq(xd)=dηd(0)+1. 对于代数数α,我们知道degα=[Q(α):Q]. 故

引理3.1degSq(xd)=degηd(0).

关于多项式φd(x),Myerson[11]证明了如下定理.

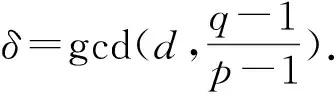
(5)

或者不可约,或者是某个多项式的完全方幂,其中k=0,1,…,δ-1.

为了得到高斯和的次数,我们先证明两个引理.

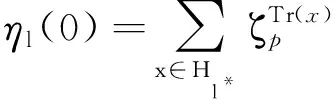
引理3.3若kl|(q-1),则

ηl(0)=ηkl(0)+ηkl(l)+…+ηkl((k-1)l).

引理3.4若f(x)=xn+an-1xn-1+…+a1x+a0是Z上多项式的k次方,则k|gcd(an-1,n).

证明 设

xn+an-1xn-1+…+a0=

(xl+bl-1xl-1+…+b0)k.

比较等式两边xn-1的系数可得an-1=kbl-1,故k|an-1. 显然k|n,所以k|gcd(n,an-1).证毕.

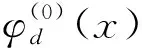
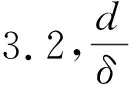
由定理2.2可知Sp2(xδ)=-p或(δ-1)p.

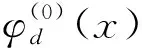
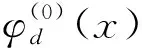
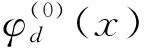
gcd(δp-p-1,m)=gcd(δ-2,m).

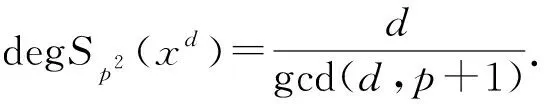
综上,我们有定理3.5.

定理3.5设p≡1(mod 4),d|(p2-1). 若d为偶数或d为奇数且gcd(d,p+1)-2与gcd(d,p-1)互素,则