不同雷诺数下二维翼型尾涡脱落的流动分析
2020-12-03杨筱沛王威蒋博彦丁炎炎王军
杨筱沛 王威 蒋博彦 丁炎炎 王军
(华中科技大学 能源与动力工程学院,湖北 武汉 430074)
翼型在低雷诺数下气动性能的好坏,是无人机、微小型飞行器等能否稳定运行的关键[1]。流体在低雷诺数下流经翼型时易出现较大的流动分离[2],在翼型前缘、尾缘处形成不同形态的涡旋,使翼型出现阻力系数增加、升力系数非线性变化等[3- 4]对气动性能的负面影响[5- 6]。深入研究翼型在低雷诺数下的尾涡脱落特性,可以加深对翼型绕流及分离形态的认识,对改善翼型在低雷诺数下的气动性能具有积极意义。
Genç等[7]通过热线实验和烟线实验,对NACA4412翼型在3种低雷诺数下的流动分离和尾涡脱落现象进行观察,发现分离泡随着翼型攻角的增加不断向前缘移动,伴随着翼型升力的不断下降。O’Meara等[8]研究了8°~12°攻角下雷诺数Re为50 000~200 000时的NACA663-018翼型,发现雷诺数和扰动环境对翼型压力分布有较大影响。Ahmed等[9]在低湍流度运动地面风洞中研究了NACA4412翼型的流动特性,通过改变攻角和离地间隙得到了机翼表面的压力分布。Kim等[10- 11]采用边界层可视化和静态压力测量方法对NACA0012翼型在低雷诺数(Re=2 300,3 300,4 800)和低攻角(α=0°~6°)下的边界层特性和气动性能进行了研究,揭示了不同低雷诺数下的流动特性。
为进一步研究翼型发生流动分离时的气动特性和流动现象,许多学者对此进行了数值研究。Martinat等[12]采用OES(Organised Eddy Simulation)和DDES(Delayed Detached Eddy Simulation)模拟研究了NACA0012翼型在雷诺数为105和106时的动态失速现象。Alferez等[13]则采用高精度LES模拟方法对同样问题进行了研究。Almutairi等[14]和Eljack等[15]分别研究了NACA0012翼型在近失速工况下和较小攻角下的层流分离泡的气动特性,观测到了低频自激振荡现象。Lei等[16]通过有限体积法求解URANS方程,研究了低雷诺数下SD8020翼型表面非定常气泡破裂和涡脱落的过程。Sreejith等[17]则采用γ-Re0模型对106雷诺数下的E216翼型进行仿真,模拟了不同攻角下层流分离泡的表现形态。
上述实验和数值研究表明,低雷诺数下的翼型流动在不同工况下会呈现截然不同的状态,但翼型尾涡脱落形态随攻角与流速的总体变化规律仍值得进一步探究和分析。文中针对此问题,采用自编网格对多个雷诺数和攻角下的NACA4412翼型进行二维非定常数值模拟,探讨了不同攻角下的气动特性,分析了翼型尾涡脱落机制及尾涡脱落与翼型升、阻力变化的联系,以期为翼型的气动优化设计与表面流动的分离控制提供思路。
1 数值方法
1.1 控制方程及湍流模型
在不可压条件下,雷诺数时均化的N-S方程形式如下:
(1)
(2)
式中,ρ、t、μ、p分别为密度、时间、黏性系数和压力,Si为自定义源项。文中利用Fluent对流场进行非定常求解。选择k-ωSST(Shear-Stress Transport)模型作为文中的湍流模型,该模型增加了横向耗散倒数项,包含转捩和剪切选项,在流场中可获得更准确的流动细节。
1.2 网格生成方法
文中基于Hermite插值函数生成代数网格。利用结点位置及其一阶导信息,控制边界附近网格的正交性[18],具体形式如下:
(3)
(4)
rTFI(ξ,η)=F1(ξ,η)+F2(ξ,η)
(5)
式中,rξ、rη分别为边界r对ξ、η(ξ、η分别为计算域的两个方向)的一阶导数,F1为ξ向物理域的单向插值,F2为η=ηj线上的差在η上的单向插值,Hi和Hj为插值基函数,rTFI为插值计算结果。
为获得物理域上的网格节点分布,控制计算域Q(ξ,η)的节点在ξ向和η向均匀分布,如图1所示,则计算域上任意位置(i,j)处有:ξi,j=i/n;ηi,j=j/m;i=0,1,…,n;j=0,1,…,m。将计算完成的计算域Q(ξ,η)代入插值基函数Hi(x)和
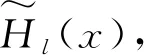

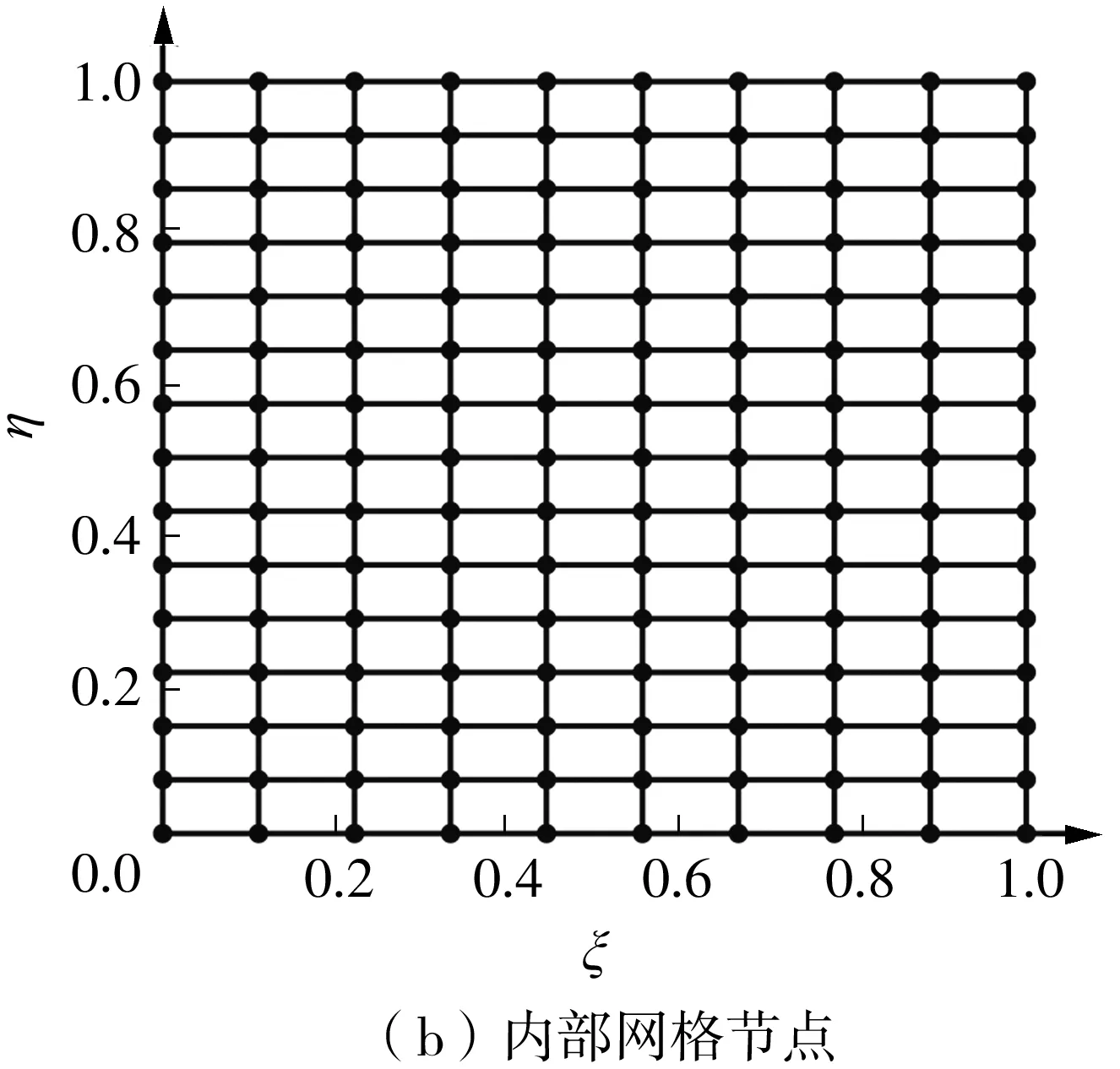
图1 计算域网格节点Fig.1 Grid nodes in computing domain
1.3 数值方法及验证
计算域及网格如图2所示。翼型弦长为L,计算域进口边界呈半圆形,距翼型尾缘10L,出口边界距翼型尾缘20L。边界条件设置为速度进口与压力出口,翼型表面无滑移。来流速度U=10 m/s。雷诺数、斯特劳哈尔(Strouhal)数St、升力系数、阻力系数、压力系数的定义分别如下:
Re=ρUL/μ
(6)
St=fL/U
(7)
CL=2FL/(ρU2L)
(8)
CD=2FD/(ρU2L)
(9)
Cp=2p/(ρU2)
(10)
式中,f为涡脱落频率,FL、FD分别为翼型表面升力和阻力,p为翼型表面压力。
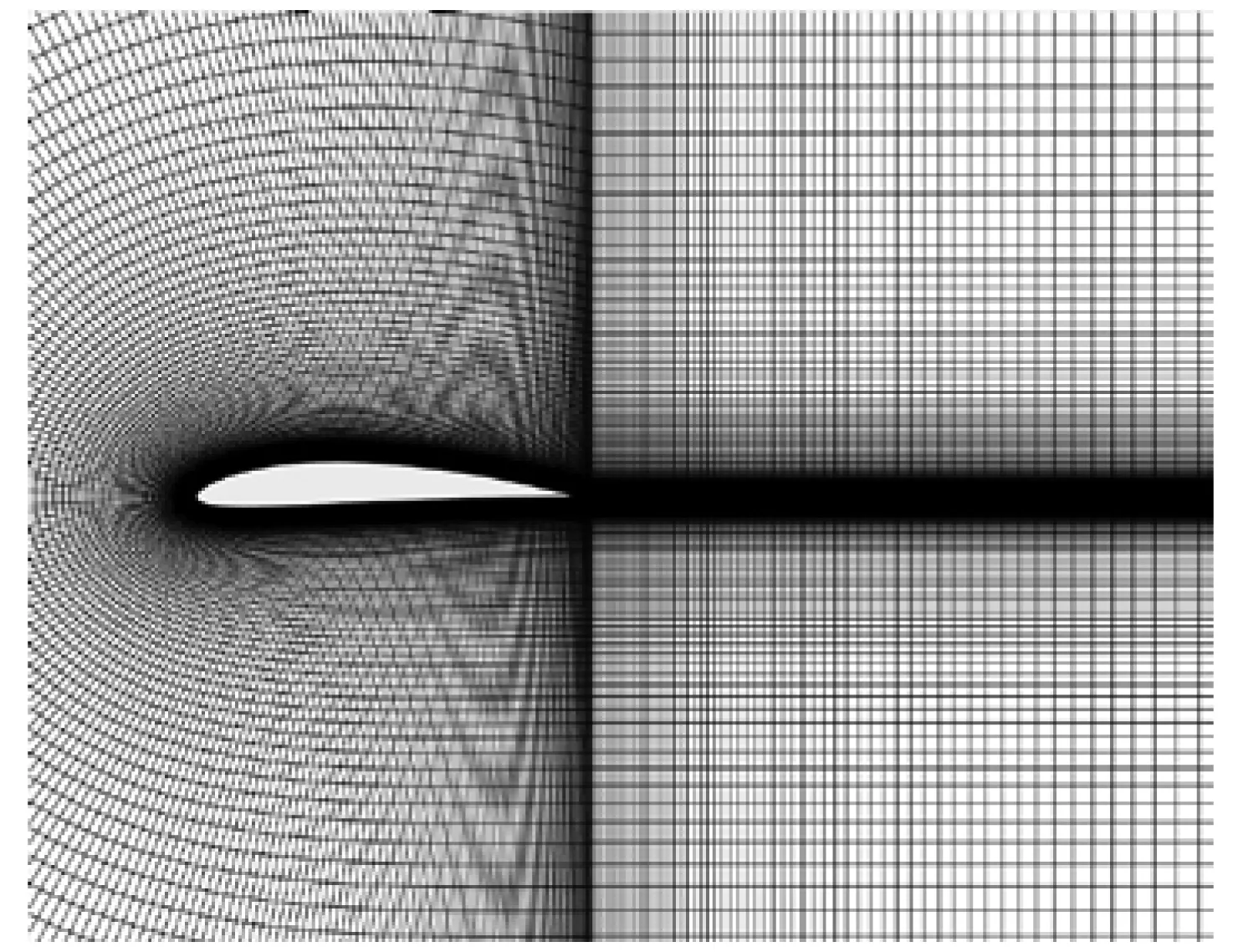
图2 计算域及网格Fig.2 Computing domain and grids
为进行网格无关性验证,分别设计了111×404、131×484、151×564和181×624共4组网格,在雷诺数为1.52×106时进行计算,并与Coles等[19]测得的数据进行对比。如图3(a)所示,4组压力系数与文献[19]实验结果均较为符合。为清晰显示流动细节并节约计算资源,文中选取151×564网格进行计算。如图3(b)所示,进一
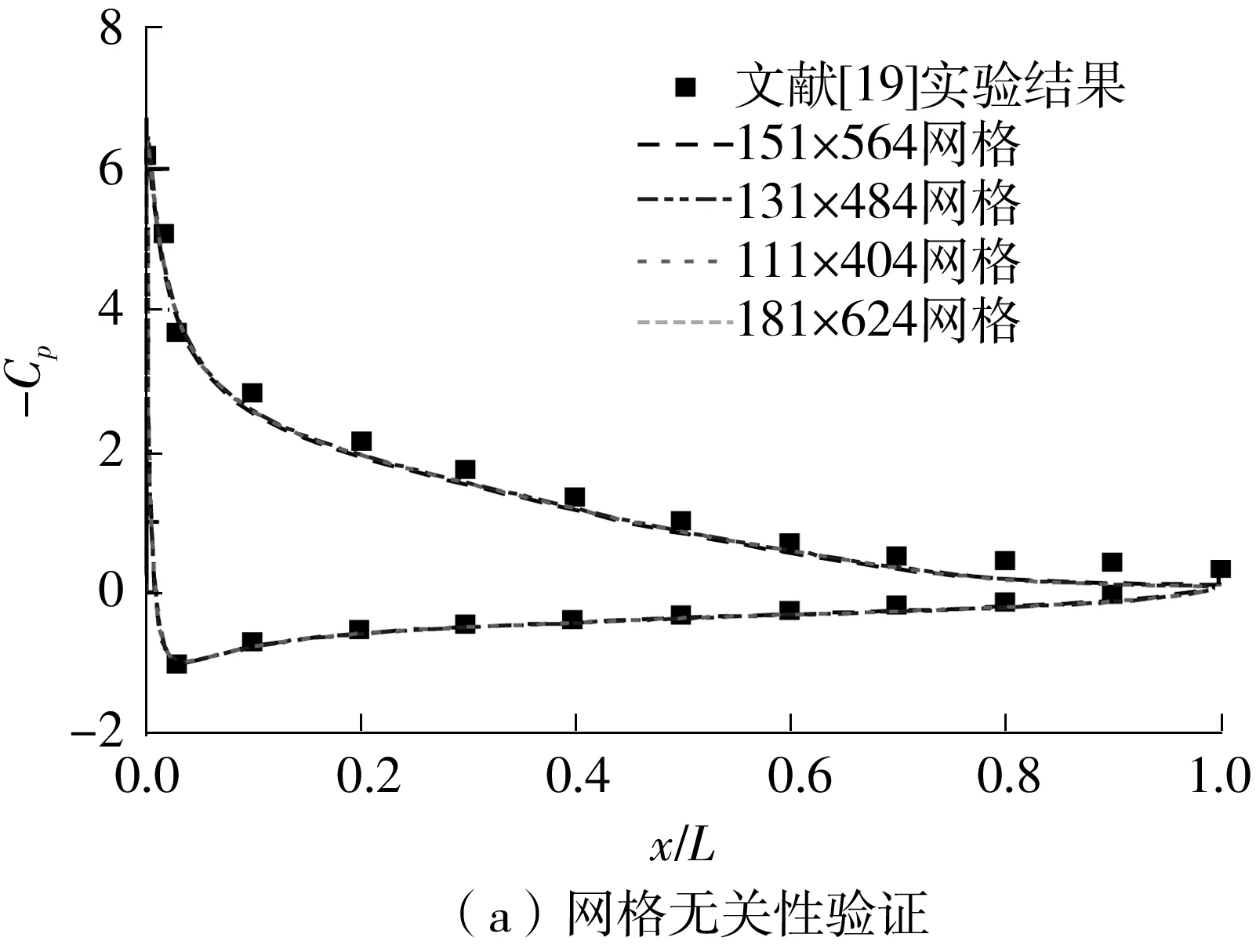
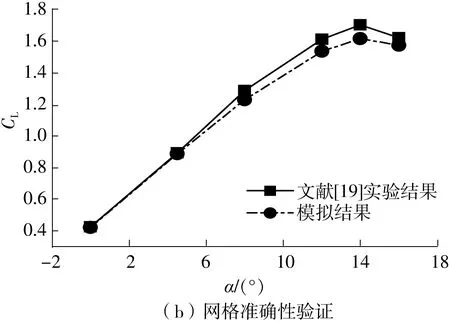
图3 网格无关性与准确性验证Fig.3 Grid independence and accuracy verification
步将该组网格在不同攻角下的升力系数与文献[19]数据进行对比,发现模拟结果与文献[19]实验结果的最大误差在3%以内,表明该网格可较好地模拟实际流动。
2 低雷诺数下翼型尾涡脱落现象及机理分析
2.1 雷诺数对翼型Strouhal数的影响
分别计算了翼型在雷诺数为5×104、1×105、2×105和5×105时的流动情况。在不同雷诺数下,随着攻角α的增大,翼型尾流出现Hopf分叉,从稳态流动转变为周期性流动。随着雷诺数的增大,流体的动能逐渐增大,对逆压梯度的抵抗能力也逐渐增强,同时,流体的黏性效应也随着雷诺数的增大而下降,导致翼型出现周期性流动时的攻角随之增大。不同雷诺数、不同攻角下的翼型Strouhal数如图4所示。Strouhal数随攻角的变化曲线随着雷诺数的增大而向右移动,相同攻角下翼型的Strouhal数随雷诺数的增大而不断增大;不同雷诺数下的Strouhal数均随着攻角的增大而不断减小,并在某一攻角显著下降,出现周期倍增现象。由图4还可知,雷诺数为5×104、1×105、2×105和5×105时,翼型尾涡脱落频率分别在α>20°、α>20°、α>21°和α>22°时降至原来的1/2左右,不同雷诺数下的Strouhal数保持在0.240 0左右。

图4 不同雷诺数下翼型Strouhal数随攻角的变化曲线
为进一步研究Strouhal数随雷诺数的变化规律,对19°攻角时翼型在不同雷诺数下的瞬态流动进行分析,此时在各雷诺数下翼型均处于升力最大值,如图5中点1、2、3、4所示,其中横坐标T=tU/L,为无量纲时间。由图4可以知道,雷诺数分别为5×104、1×105、2×105和5×105时,NACA4412翼型在19°攻角下的Strouhal数分别为0.559 8、0.559 9、0.737 4和0.919 8。为加强对流场细节的理解,对流场中的涡量进行统计。其定义及计算方式如下:
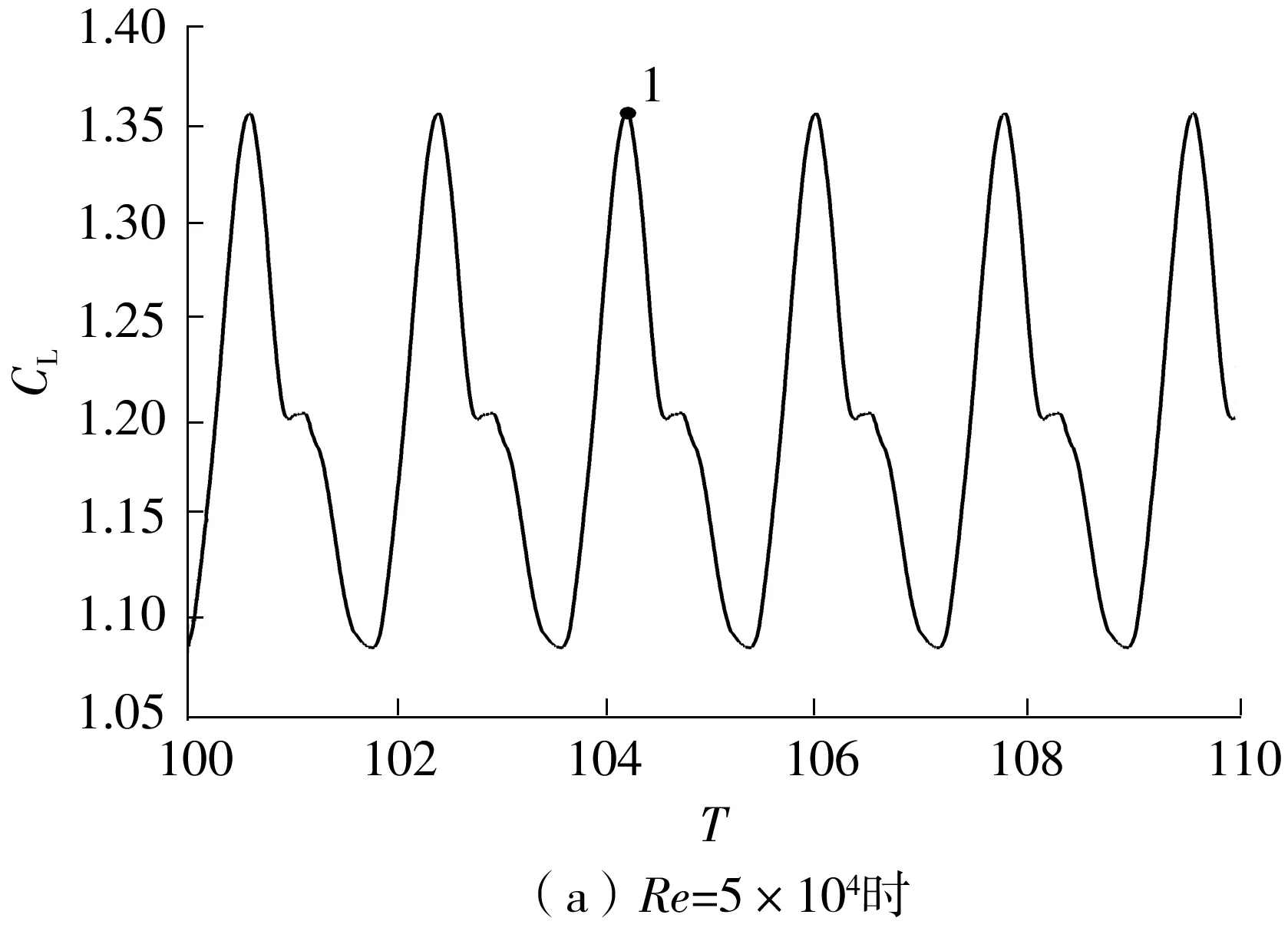
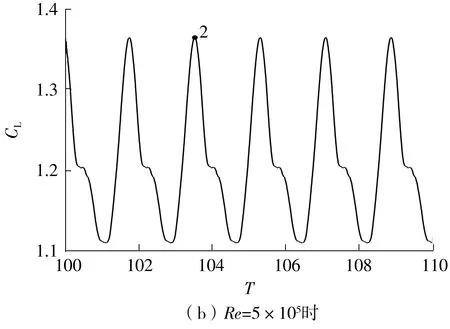
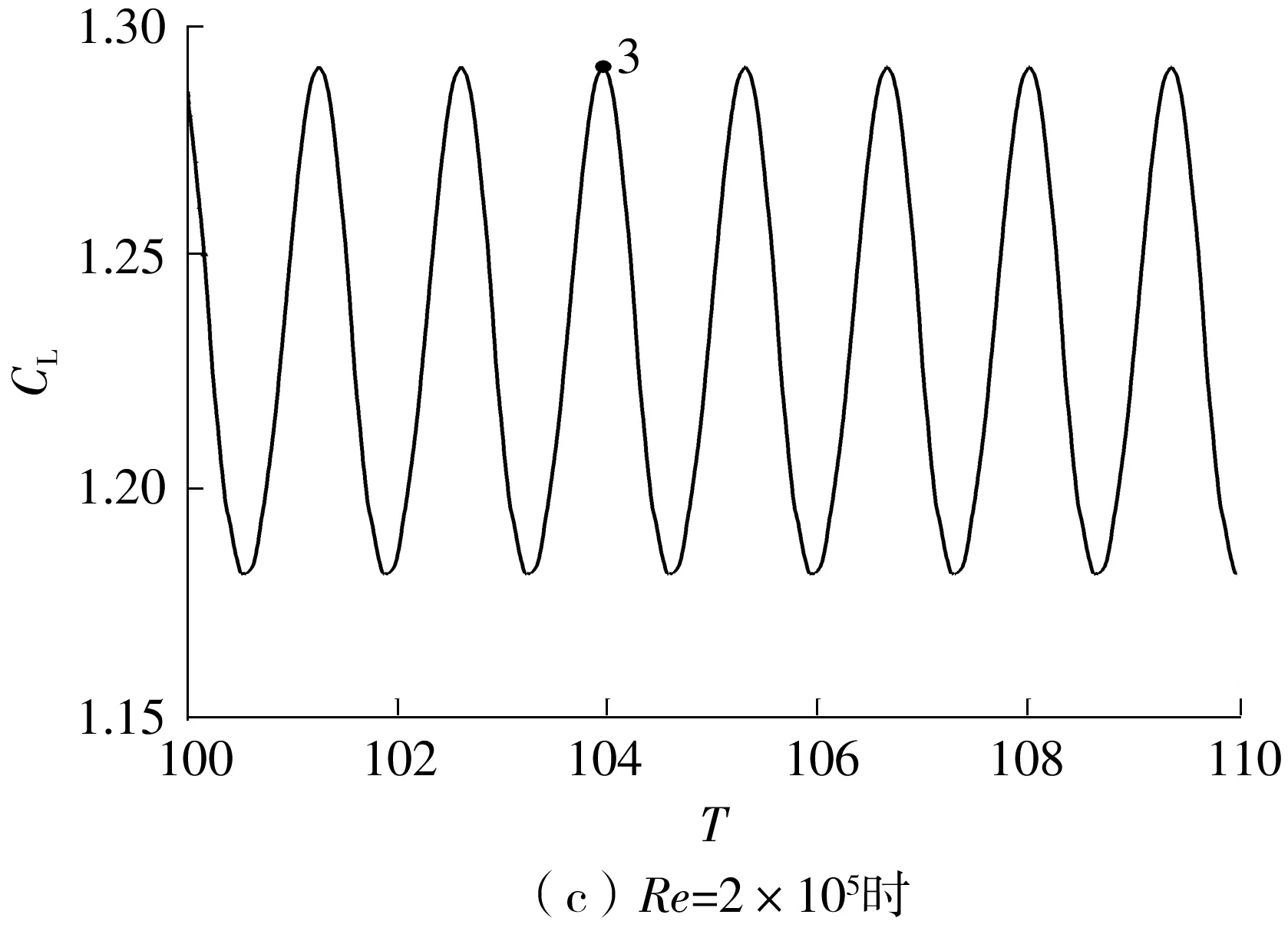
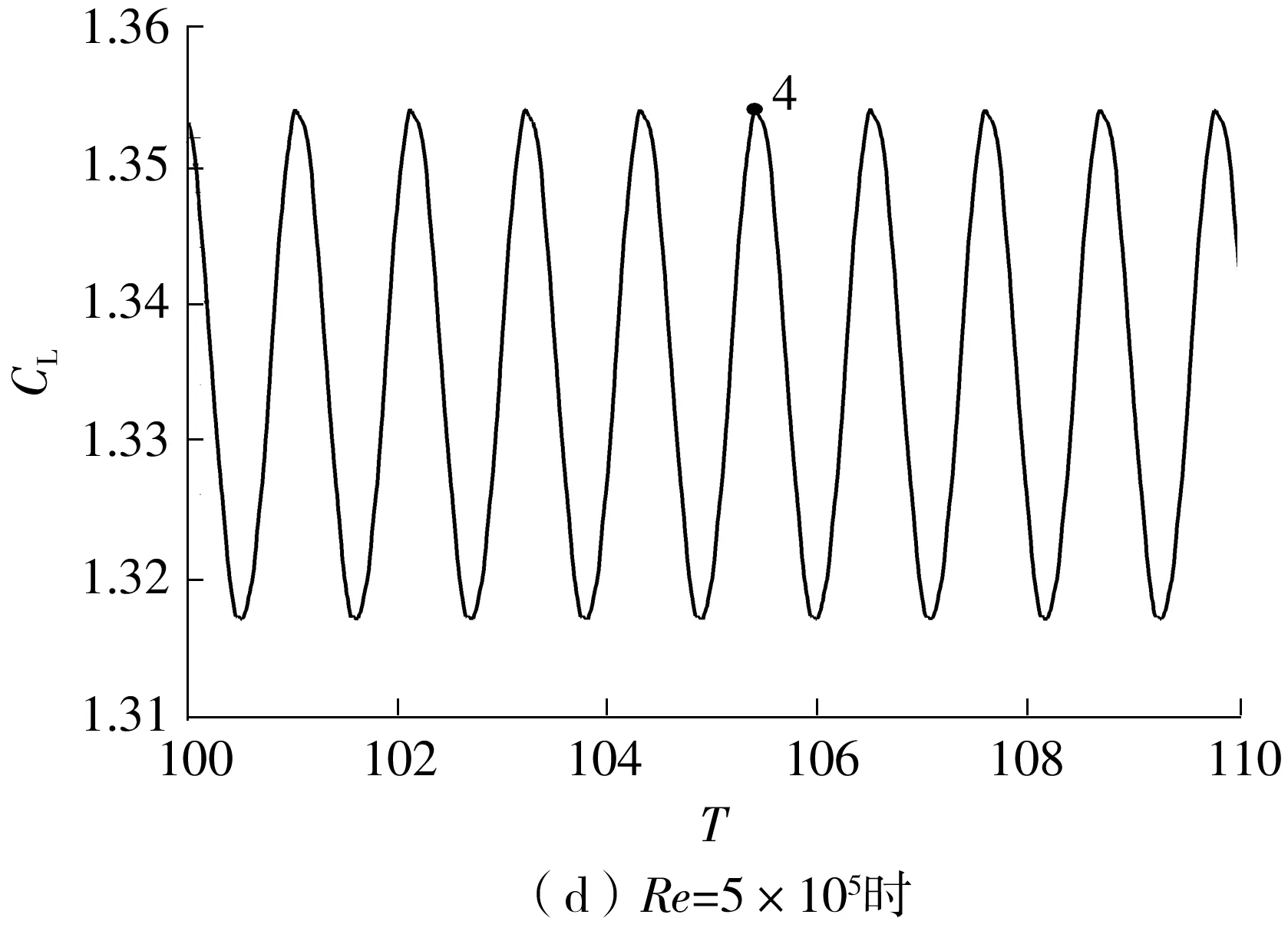
图5 19°攻角时4种雷诺数下翼型升力系数的时域图
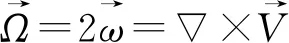
(11)
(12)
式中,u、v分别为来流速度U在x、y方向的分量。图6所示的瞬态流动结果表明,随着雷诺数的增大,翼型的流动状态发生了明显变化。
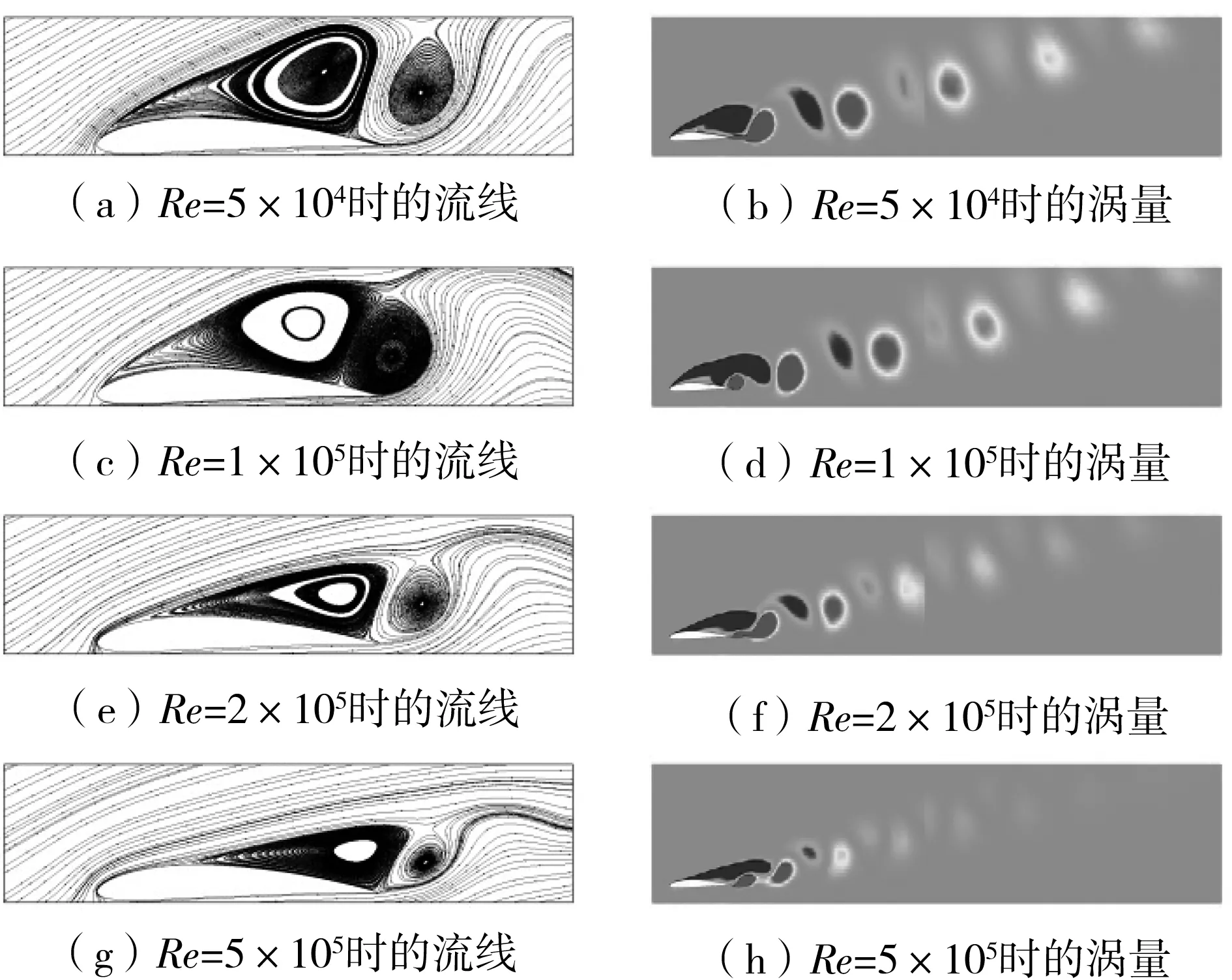
图6 4种雷诺数下翼型瞬态流线图与涡量云图
当雷诺数较低(Re=5×104)时,翼型上表面流动结构较差,分离区从翼型前缘处出现并形成大尺度分离泡。原因在于此时流体动能较小,无法抵抗较大的逆压梯度。同时,翼型上表面存在一因主分离涡诱导形成的小尺度二次涡,如图6(a)所示。此时主分离涡的漩涡强度较高,对主流具有较强的卷吸作用,因流体具有较强的黏性效应,漩涡与主流之间的作用时间更长,漩涡强度衰减得更慢(见图6(b))。同时,因翼型上表面分离涡的分离位置十分靠前,其脱落之前向下游移动的速度更低,距离更长,从而导致此时翼型尾涡的脱落周期更长。随着雷诺数的增大,流体的黏性效应减弱,流动分离得到缓解。如图6(e)所示,当雷诺数增大到2×105时,翼型上表面分离泡明显变小,分离起始点向下游移动。随着流动对逆压梯度的抵抗不断加强,主分离涡的强度及对主流的卷吸能力均逐渐降低(见图6(f))。此时,主分离涡可较快完成形成—发展—脱落过程,从而使翼型的尾涡脱落频率加快。当雷诺数进一步增大(Re=5×105)时,翼型上表面分离涡尺度和强度继续减小,分离位置从前缘点后移至翼型30%处(见图6(g)和图6(h)),流体分离得到进一步改善。归根结底,黏性效应的降低是同攻角下翼型Strouhal数随雷诺数增大而增大的根本原因。
2.2 低雷诺数下翼型非定常气动特性及尾涡脱落机制分析
如图4所示,不同雷诺数下翼型的Strouhal数均在22°攻角附近显著下降,出现周期倍增现象。22°攻角时翼型在雷诺数为5×104、1×105、2×105和5×105时的Strouhal数分别为0.250 0、0.244 5、0.237 5和0.519 9,Re=5×105时翼型在23°攻角下的Strouhal数为0.228 5。为对这一周期倍增现象进行深入研究,选取翼型在各雷诺数攻角下的流动为对象进行分析。4种雷诺数下翼型的非定常升力系数时域图如图7所示。
图7(a)-7(c)中,升力系数的波动均出现周期倍增现象,波动频率基本不变,但波动幅值随着雷诺数的增大而逐渐减小,雷诺数为5×104、1×105和2×105时的波动幅值分别为0.580 66、0.580 34和0.472 75。Re=5×105时,翼型升力系数的波动范围和周期均明显减小,波动幅值仅为0.247 33。对不同雷诺数下的升力系数分别进行如图7所示的特征标记(点1-5),进一步研究翼型的气动特性变化规律与尾涡脱落的关系。
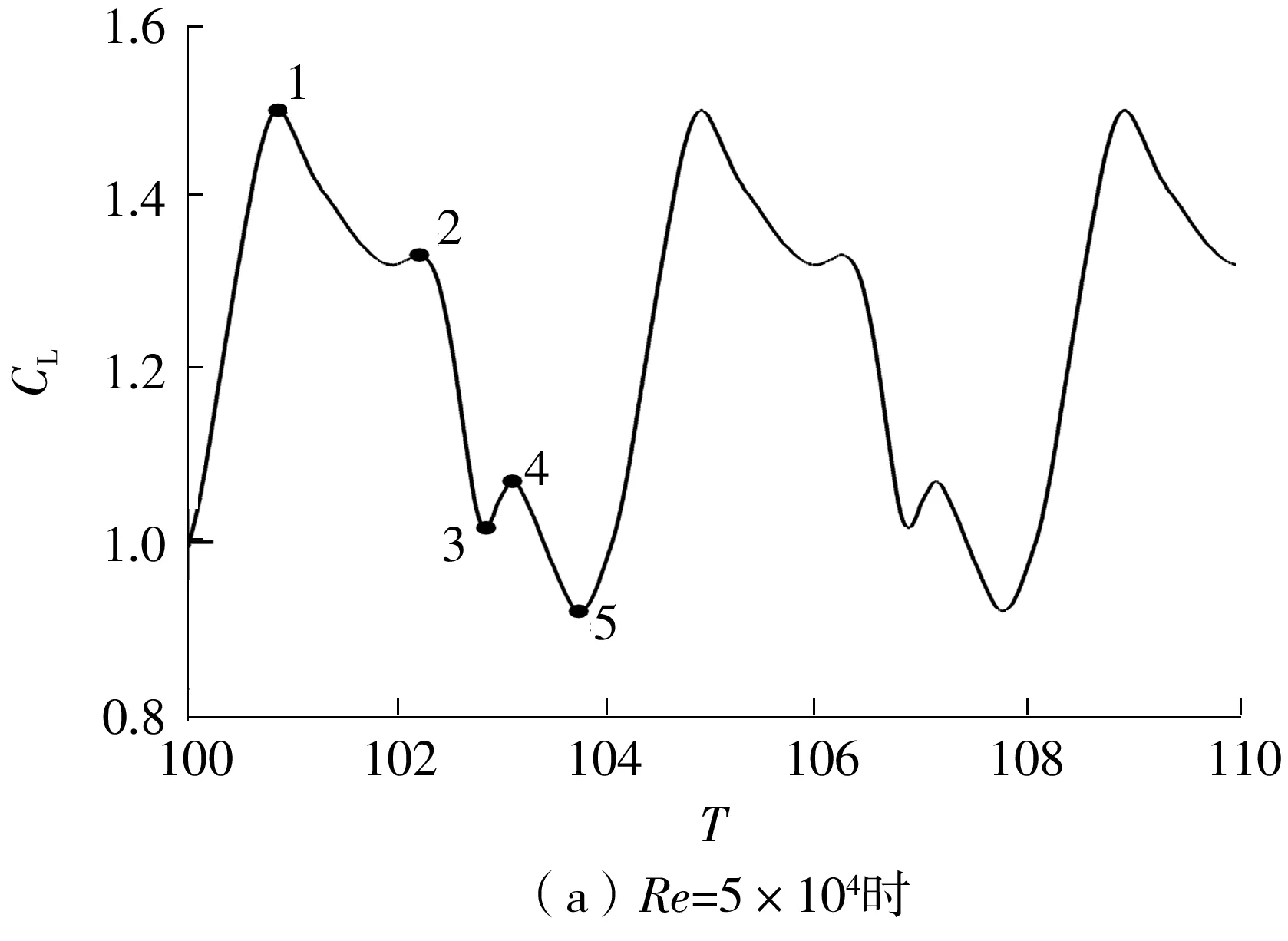

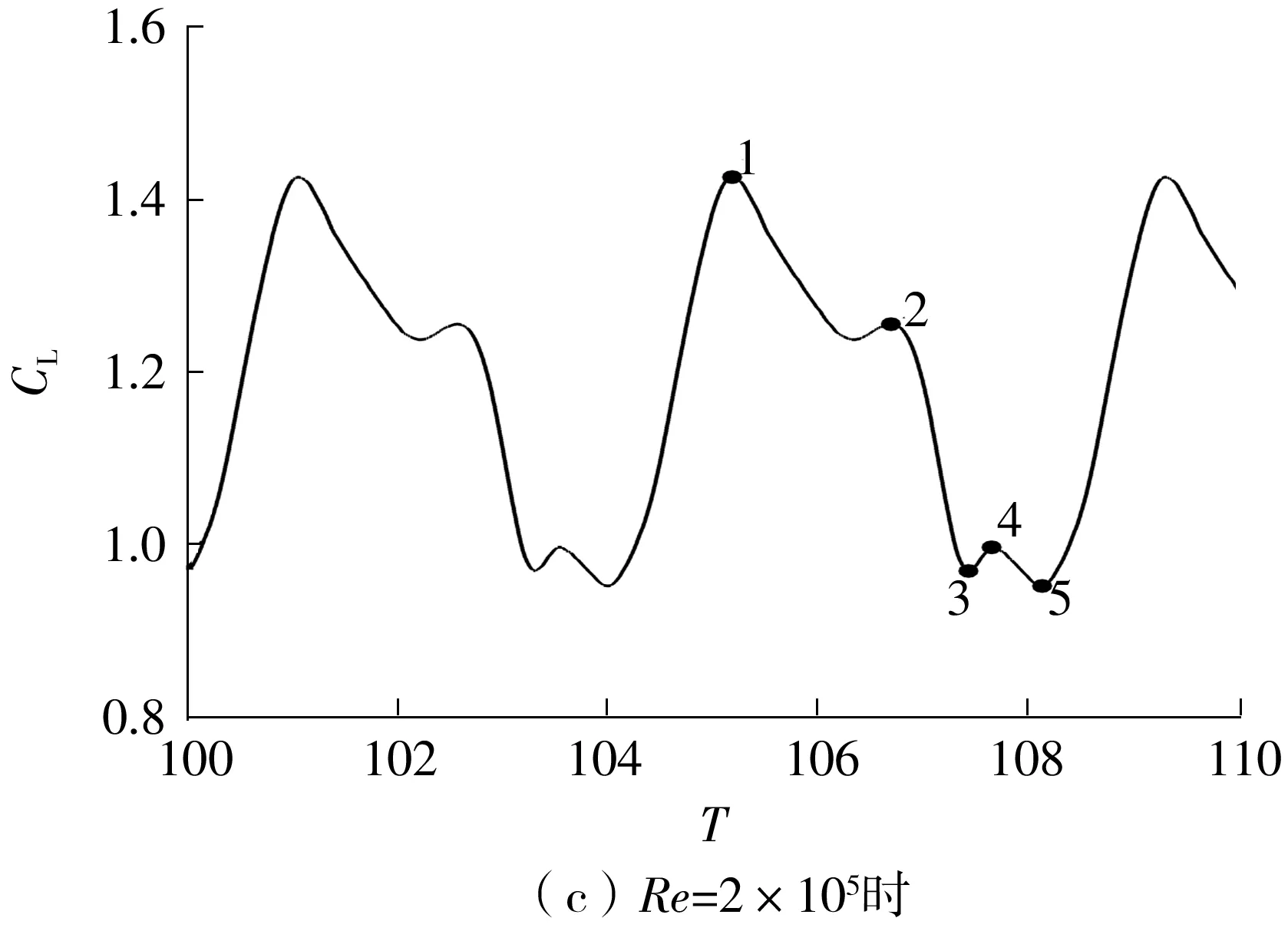
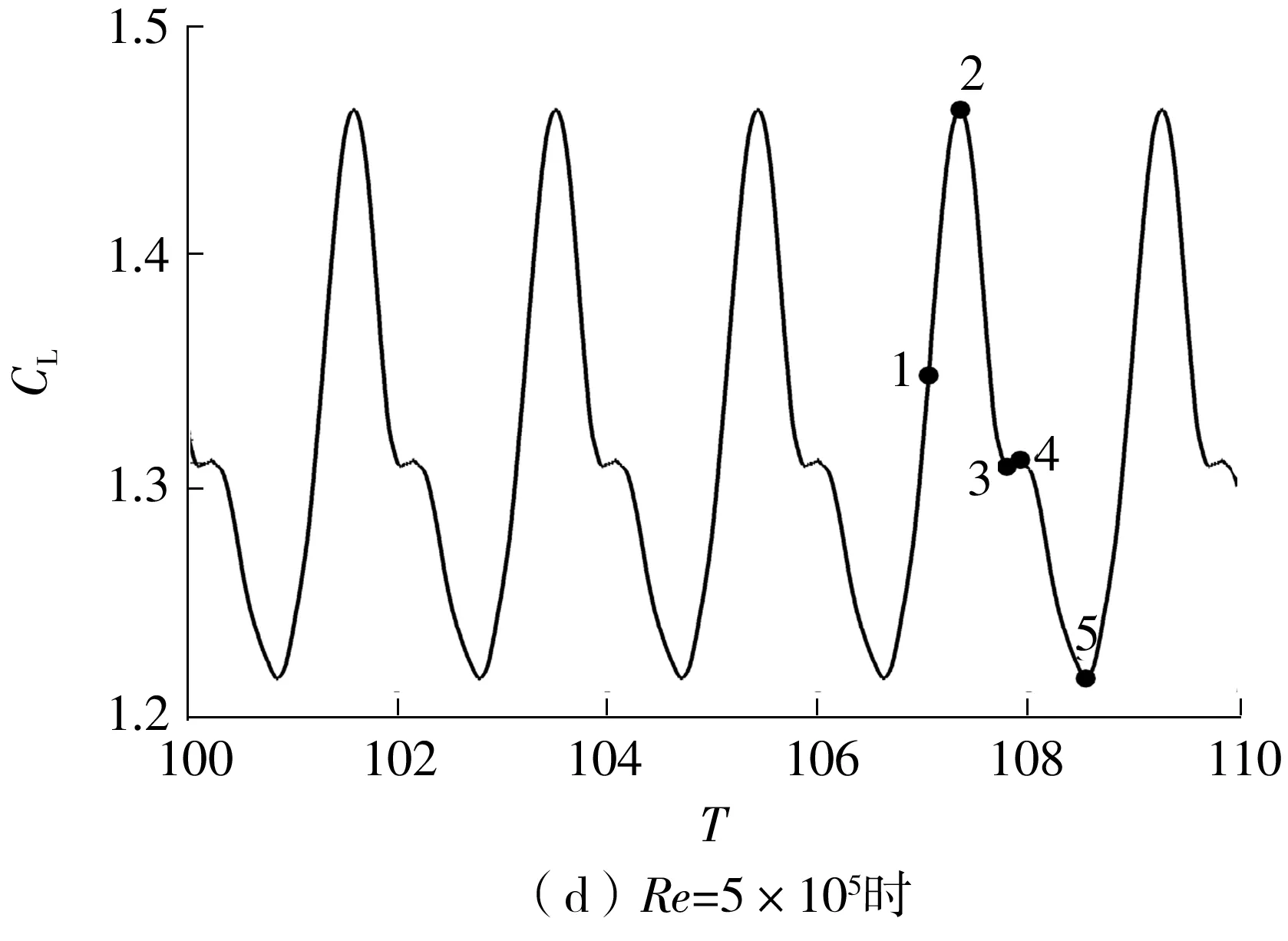
图7 4种雷诺数下翼型的非定常升力系数时域图
不同雷诺数下,翼型在各个特征点时刻的流线图及涡量云图如图8所示。Re=5×104条件下,由图8(a)和8(b)可见,点1时翼型的升力系数达到峰值1.500 55,此时翼型尾部第1次已成型的逆时针涡的中心强度达到106.391 s-1,处于即将完全脱落的状态;流体流经翼型下表面,在尾缘处因翼型上表面的大尺度分离涡诱导,向上卷吸并开始形成1个新的逆时针涡。该涡刚刚形成,因而具有较大强度,为613.784 s-1。随着尾缘处逆时针涡的发展,翼型上表面的大尺度分离涡被分割成前缘驻留涡与尾缘主分离涡两部分。吸力面二次涡发展到最大时,强度为68.196 s-1,此时前缘驻留涡同样被分割成两个强度接近、分别为-96.165 4 s-1和-57.832 1 s-1的小尺度顺时针涡,此时翼型升力系数在随着尾缘逆时针涡的增大而不断减小后出现点2处的局部最大值1.332 93。随着尾缘逆时针卷吸涡的继续增大,吸力面二次涡开始逐渐减小,两个小尺度顺时针涡随之重新融合,形成1个前部强度较强、后部强度较弱,且最低强度为-245.113 s-1的大尺度分离涡,翼型上表面的尾缘主分离涡不断向下游移动。当主分离涡即将从尾缘脱落时,翼型升力系数出现点3对应的局部最小值1.016 60。此时,主分离涡与之前脱落的逆时针涡形成1对旋向相反的涡对。当尾缘处的逆时针涡继续发展至即将脱落时,翼型升力系数缓慢回升,出现局部最大值(1.070 42,点4)。当尾缘处再一次卷吸形成逆时针涡并达到最大时,该逆时针涡的强度达到249.242 s-1,且翼型的升力系数达到谷值0.919 89(点5)。同时,该逆时针涡对翼型上表面分离涡进行挤压,随着时间的推移将其切割成1个新的较小的脱落涡,此逆时针涡与脱落涡形成第2对旋向相反的涡对。


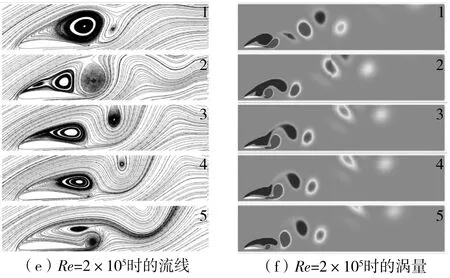

图8 4种雷诺数下翼型单周期内的流线图与涡量云图
由图8(c)-8(f)可知,Re=1×105和Re=2×105时翼型的升力变化与翼型尾涡脱落规律之间的联系与Re=5×104时的基本一致。但随着雷诺数的增加,翼型上表面的二次涡、分离涡和尾缘处卷吸形成的逆时针涡的强度均逐渐减小。
在雷诺数为5×104、1×105、2×105时,翼型上表面的大尺度分离涡均在吸力面表面二次涡与尾缘处逆时针涡的共同作用下被尾缘处逆时针涡切割两次,先后形成两对强度有明显差异的反向旋转的涡对并脱落,出现2P(Pair)脱落模式,这也是在每个周期内升力系数出现两次振荡循环、Strouhal数出现周期倍增现象的原因。
当Re=5×105时,由图7(d)可知,翼型升力系数的波动规律与其他3种雷诺数下的波动规律明显不同,波动频率约为后者的1倍。在此雷诺数下,流体具有较大动能,黏性效应显著下降,流经翼型时发生的流动分离现象明显得到改善。此时翼型吸力面二次涡完全消失,翼型只存在1个大尺度分离涡和由其引起的尾缘卷吸涡相互作用。在特征点1时,翼型尾缘处的逆时针涡处于缓慢向下游脱落阶段,与此时翼型升力系数处于上升阶段趋势一致。当尾缘处强度为182.378 s-1的逆时针涡刚刚脱落时,翼型升力系数达到最大1.463 53(点2);尾缘处新卷吸的逆时针涡在强度达到319.375 s-1时于吸力面上生成至最大,此时翼型的升力系数出现最小值1.216 31(点5);这些现象均与前文所述的规律一致。此时,在1个周期内,翼型吸力面前缘分离产生的顺时针涡与翼型压力面卷吸产生的逆时针涡交替脱落1次,形成1对旋转方向相反的2S(Single)涡对。这与翼型升力系数在1个周期内出现1次振荡循环、Strouhal数此时均未出现周期倍增现象相符,也再次说明翼型升力系数的变化与翼型尾涡脱落规律有密切关系。
2.3 低雷诺数时翼型在不同攻角下的尾涡脱落演变规律
由前文可知,不同雷诺数下翼型的Strouhal数均随着攻角的增大而不断减小,随后出现周期倍增现象。为进一步探讨低雷诺数时翼型在不同攻角下的尾涡脱落发展规律,本节以雷诺数Re=1×105的情形为例,分析翼型在不同攻角下的尾涡脱落形态。图9为Re=1×105时翼型在不同攻角下的Strouhal数曲线。
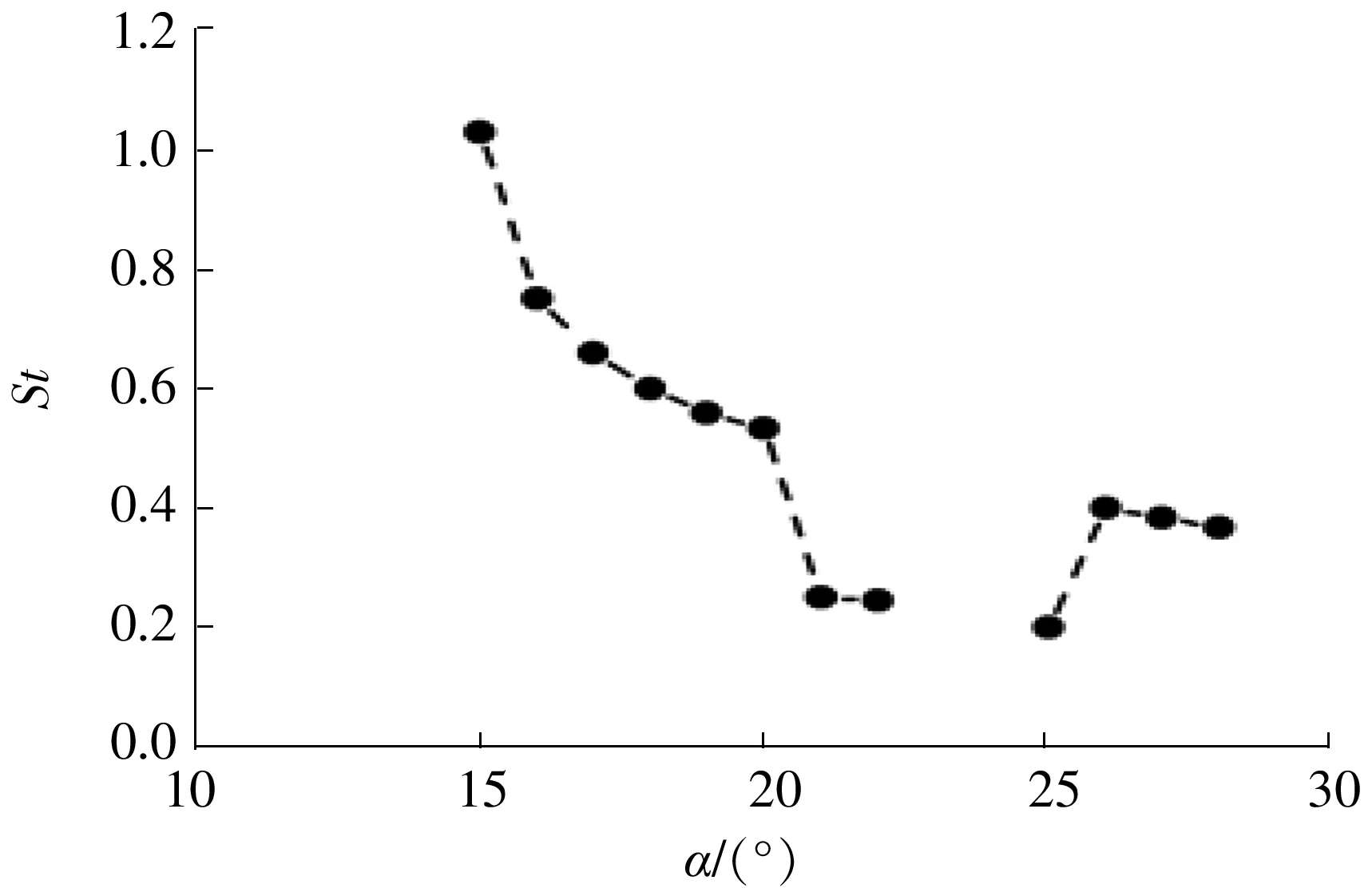
图9 Re=1×105时翼型在不同攻角下的Strouhal数曲线
由图10可知,攻角α=15°时,频谱图上仅有1个主频,其对应的Strouhal数为1.028 3,翼型尾部流动脱落十分微弱,升、阻力系数随时间的变化接近于正弦振荡,表明翼型刚由定常流动转变为非定常流动。随着攻角的不断增大,翼型升、阻力系数随时间的变化曲线由正弦振荡向非正弦振荡持续发展,非正弦振荡不断加剧。升力系数的频谱图中开始出现谐波频率,且其数量随攻角的增大而不断增多。到α=20°时,升、阻力系数随时间的变化表现出典型的非正弦振荡,其主频对应的Strouhal数持续减小至0.533 2,并出现幅值约为主频幅值1/2的谐波频率。在此阶段,翼型尾缘在每个周期只形成1对旋向相反的2S涡对。当α增大到22°时,频谱图上出现次谐波频率,其频率为主频(f=2.445)的1/2,即出现周期倍增现象。此时,翼型尾涡结构转变为两对逆向旋转的2P模式的涡对。其具体形成过程已在前文描述,此处不再赘述。

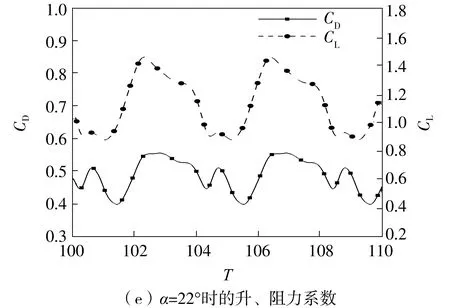
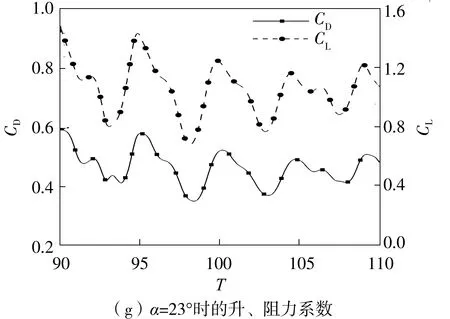

随着攻角增大到23°,翼型流动进入混沌状态。此时频谱图上存在着多个幅值相当的频率,分别为0.272、2.182和4.272,且无明显主频;从升、阻力系数时域图上可看出单个周期内升、阻力系数的振荡区间和变化形态存在显著差异。当攻角继续增大到25°时,翼型流场重新恢复至周期性流动,此时频谱图上存在1个明显的次谐波,其对应的Strouhal数为0.200 0,记此种流动为准周期性流动。
由此可知,翼型进入周期性流动后,尾涡脱落随着攻角的增大将呈现2S模态—2P模态—混沌状态—准周期性流动的发展规律。不同雷诺数下尾涡脱落形态与攻角的关系如图11所示,可发现各雷诺数下脱落形态均表现出如前所述的发展规律,仅因黏性系数随着雷诺数的增大而降低,导致各个临界点对应的翼型攻角逐渐增大。
3 结论
(1)通过模拟NACA4412翼型在不同攻角和雷诺数下的流动特性,发现随着攻角的增大,翼型由定常流动转变为周期性流动。出现周期性流动后,流体黏性效应的降低导致相同攻角下翼型的Strouhal数随雷诺数的增大而不断增大;不同雷诺

图11 不同雷诺数下NACA4412翼型流场形态随攻角变化的示意图
数下的Strouhal数均随着攻角的增大而不断减小,并在某一攻角显著下降,出现周期倍增现象。
(2)不同雷诺数下,翼型升力系数的变化规律与翼型尾涡脱落规律保持一致。翼型尾缘脱落1对2S涡对时,翼型升力系数单周期内振荡循环1次;翼型尾缘脱落2P涡对时,升力系数单周期内振荡循环两次。翼型升力系数峰值出现在尾缘逆时针涡刚脱落完毕时,谷值出现在尾缘逆时针涡发展至最大时。
(3)不同雷诺数下,翼型在进入周期性流动后,尾涡脱落均随着攻角的增大呈现2S模态—2P模态—混沌状态—准周期性流动的发展规律,因流体黏性系数的降低导致临界点时对应的翼型攻角逐渐增大。
