降雨非饱和入渗对土壤热量运移变化的影响

张 超，姜景山，王如宾，金 华

降雨非饱和入渗对土壤热量运移变化的影响

张 超1,2，姜景山1，王如宾3，金 华1

（1. 南京工程学院 建筑工程学院市政工程系，南京 211167；2. 南京工程学院 建筑工程学院岩土工程研究所，南京 211167；3. 河海大学 岩土工程科学研究所，南京 210098）

高温季节土壤表层温度非常高，土壤内部含水率较低，突发性降雨对于土壤温度动态变化和水热交换运移影响极大。为了揭示降雨非饱和入渗对土壤热量运移变化的影响，该研究建立了反映降雨入渗过程的土壤热量运移数学模型，编制了有限元数值计算程序，针对南京雨花台区典型土壤，开展了降雨非饱和入渗对土壤热量运移影响的数值计算与分析研究。结果表明：不考虑降雨入渗情况下，土壤温度变化与热量运移主要是表层土壤与环境之间的热交换作用引起，热量运移影响深度约0.2 m；降雨强度45 mm/h作用下，随降雨历时增加，雨水全部自由入渗到土壤内部，土壤内部基质吸力呈线性递减趋势，湿润锋面逐渐下移，土壤体积含水率快速增加；湿润锋过后的土壤体积含水率逐渐接近于饱和体积含水率，土壤入渗能力逐渐下降，直至趋于饱和入渗率；在降雨非饱和入渗影响下，入渗到土壤孔隙中的低温雨水与土壤颗粒发生热量交换，进而改变了原有土壤温度场分布，并随着降雨入渗深度的持续增加，降雨入渗过程对土壤热量运移的影响呈现逐渐减弱趋势。经过现场实测数据与模拟计算结果验证，随着降雨历时增加，土壤体积含水率实测值和数值计算值相对误差保持在±3.99%以内，均方根误差RMSE为0.01 cm3/cm3；土壤温度实测值和数值计算值的相关误差保持在±2.72%以内，均方根误差RMSE为0.55℃，模拟计算结果和现场实测数据均吻合较好，表明该模型对描述降雨非饱和入渗过程土壤热量运移规律的适应性较强，数值计算程序合理。研究成果可为农业水利工程与水土保持、土壤水文水资源的分布与利用、城市水资源控制与生态环境保护等领域提供重要参考。

土壤；温度；热量运移；降雨非饱和入渗；水分运动；数值计算

0 引 言

每年气温最高的丰水季节，土壤表面及其浅部温度变化很大，不同降雨条件下非饱和入渗过程对土壤热量运移影响甚为明显，且影响因素众多，热量运移过程复杂。因此，研究降雨非饱和入渗过程中土壤温度变化及热量运移，对揭示降雨入渗引起土壤水热耦合运移机理具有研究意义。

目前，众多国内外学者在不同温度条件下土壤水分运动规律试验、入渗模型以及入渗机理等方面取得了丰富的研究成果[1-3]。汪志荣等[4]研究了温度影响下土壤入渗量与湿润锋的关系，认为温度在5～40 ℃范围时，粉壤土的饱和导水率从0.001 36 cm/min增加到0.004 48 cm/min，温度变化对土壤饱和导水率的影响较为明显。辛继红等[5]认为随着温度的升高，土壤湿润锋运移速率和入渗速率与温度和时间符合多元复合幂函数关系。朱红艳等[6-7]研究了不同水温对土壤入渗特性的影响，建立了不同温度水分入渗时湿润锋运移距离与入渗时间和水温的关系方程，结果显示在入渗历时400 min内地表以下15 cm深度范围的土壤温度变化更为明显。马效松等[8]开展了冻融期土壤水分动态过程模拟，结果显示各土层含水率真实值和模拟值均方根误差（Root Mean Squared Error，RMSE）位于1.01～13.54 cm3/cm3。以上研究成果对于清晰掌握土壤水热分布状况，减少土壤流失和地表径流，识别土壤水分运移及相变规律具有重要意义。

对于季节性和昼夜性气温变化较大的西北干旱地区，其冻融过程中水分的冻结和融化必将伴随着热量的交换，冻融过程水热耦合是寒区土壤水文循环与热量运移的重要内容[9-11]。陈琳等[12]采用HYDRUS软件进行了不同土壤温度和容重下微咸水上升毛管水运动特性模拟，拟合结果揭示出砂壤土各处理毛管水上升补给量与时间拟合程度较高，决定系数2均达到0.996以上，RMSE均小于2.7 cm。任杰等[13]同样采用HYDRUS软件模拟分析了不同水头低温水入渗条件下土壤水分、温度动态变化，认为入渗水头为45 cm时，土壤深层饱和区域对土壤表层湿润区的影响比低水头入渗更为显著。张明礼等[14]研究了活动层水热响应机制与过程，认为气候升温通过改变地表能量与水分平衡过程和土壤内部水热运移分量影响多年冻土水热过程。另外，温度势对土壤水分运动过程有显著影响。高红贝[15]研究认为土壤水分入渗过程中，当温度势和基质势协同时，温度的升高能明显促进土壤的水分运动。另外，冯宝平等[16-20]亦针对温度变化对土壤水分入渗过程的影响机理展开深入研究。以上成果主要研究土壤温度变化对土壤中水分运移规的影响，揭示了土壤水分运动的温度效应，但是并没有深入研究降雨入渗过程中土壤温度变化及其对土壤水热耦合运移的影响机理问题。

随着土壤水动力学理论不断完善和数值模拟技术的快速提高，降雨入渗过程对土壤温度变化及热量运移的影响机理问题研究得以进一步发展。针对降雨过程中土壤温度的变化规律，高红贝等[21]认为降雨过程对干旱区浅层土壤温度的影响要明显大于深层，降雨后随着表层土壤水分的散失，土壤温度会迅速升高，并在表层10～20 cm间会出现一个低点，但该研究尚未考虑土壤水分场与温度场的耦合问题。张超等[22]解决了坡面水流与土壤表面温度交换的问题，但是尚缺乏针对降雨非饱和入渗过程的土壤温度变化及热量运移相关研究成果。近些年发展起来的数值模拟技术是解决土壤水热耦合及其运移过程的有效手段，为此，李腾风等[23]基于格子Boltzmann方法，模拟温度场与水分场的演化过程，发现在相同热源作用下，孔隙率较小的土壤，温度升高速度较快；宫兴龙等[24]同样该方法定量分析了降雨条件下坡面水流对土壤温度分布的影响，发现坡面水流对土壤温度的前期影响主要发生在土壤表层。另外，HYDRUS软件[12-13]、CoupModel模型[25-27]等也被用来开展水热耦合的相关研究，但是以上模拟技术受到参数取值、计算精度和模型建立等多方面的约束，推广应用程度有限。因此，为了系统揭示土壤温度与水分运动相互影响机理，亟需开展反映降雨非饱和入渗对土壤热量运移变化影响的有效模拟方法与研究手段。

综合以上分析，高温季节土壤表层温度非常高，土壤内部含水率较低，突发性降雨对于土壤温度动态变化和水热交换运移影响极大，开展降雨非饱和入渗对土壤热量运移变化的影响研究非常重要。因此，本文基于土壤水分运动和热流运动基本理论，建立降雨条件下考虑温度动态变化影响的土壤热量运移数值分析模型，通过研究降雨入渗过程中土壤基质吸力与体积含水率分布规律，分析降雨非饱和入渗对土壤热量运移变化的影响，并与现场监测数据进行对比分析，验证了数值计算结果的合理性和精确性，旨在较为全面地揭示降雨入渗过程中土壤水热交换互馈作用及热量运移过程。

1 理论与方法

为了揭示降雨非饱和入渗对土壤热量运移的影响机理，需要建立反映描述土壤降雨非饱和入渗过程和热量传输过程的关系方程。

1.1 降雨入渗对土壤热量运移传输过程的影响

假定非饱和土壤水流的驱动力为基质势和重力势之和的梯度，土壤非饱和导水率是土壤含水率或基质势的函数。基于达西定律，Buckingham提出了描述非饱和土壤中水流运动Buckingham-Darcy定律[28]，其表达式为

给定降雨强度下雨水入渗是促进土壤水分运动的驱动力，改变了土壤渗流场分布。降雨入渗过程中土壤水分运动满足Richards方程，其垂向一维表现形式如下：

式中()为比水容量，cm-1；()=d/d，为土壤含水率，cm3/cm3；为时间，min。

考虑降雨入渗情况下土壤热量传递过程通常包括两部分：一是土壤颗粒之间热传导作用，二是入渗雨水所携带的热量。

根据热力学能量守恒定律，单位时间内流入单位体积内的热量必须等于单位体积内土壤吸收的热量，因此，考虑降雨入渗引起土壤温度变化的热量运移传输控制方程为

式中C为土壤的体积比热容，J/(m3℃)；ρ为土壤密度，kg/m³；表示土壤温度，℃；为土壤导热系数，J/(m℃)；C为土壤内部水的体积比热容，J/(m3℃)；ρ为土壤水流密度，kg/m³。

1.2 温度变化对土壤导水率的影响

降雨入渗过程中，土壤温度的变化直接影响降雨入渗过程中土壤水分运动的传输与运移，温度场就是通过影响土壤水流动力黏滞系数进而影响到土壤饱和非饱和渗流场的变化。Contantz等[29]等提出了土壤温度与非饱和导水率之间的函数表达式

式中(,) 为考虑温度影响的土壤非饱和导水率，m/h；为与土壤几何性质有关的内透水率，与温度变化无关；()为相对非饱和渗透率，m/h；为土壤水流动力黏度系数，Pa·s；为重力加速度，m/s2。

研究表明，土壤入渗水流的运动黏滞系数是土壤温度的函数[22]，其经验公式如下：

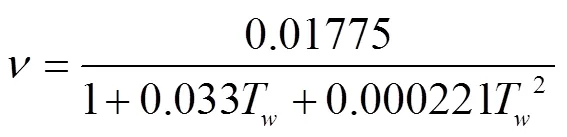
式中为土壤水流的运动黏滞系数，m2/s；T为土壤入渗水流温度，℃。

2 数学模型与求解

2.1 基本假定

降雨入渗过程中土壤温度的变化及热量的传递与运移是一个复杂的过程。为了研究方便，本文在降雨非饱和入渗对土壤热量运移影响的数值分析过程中做了如下假设：

1）将土壤视为各向同性多孔介质，暂时不考虑降雨入渗引起的土壤孔隙结构的变化，土壤骨架不发生膨胀及压缩变形。

2）降雨入渗到土壤内部的水分连续且不可压缩，入渗水流通过所携带入和传递的热量，来影响土壤温度场的分布。

3）仅考虑垂直向的降雨自由入渗情况；对于降雨积水压力入渗，由于涉及到表面径流的问题，暂时不予考虑。

4）将降雨入渗视为非饱和连续介质渗流；温度变化不引起水的相变，忽略气相的影响、蒸发、溶质势和汇源项对土壤水分运动及热量传输的影响。

2.2 数学模型

综合式（4）～（5），可以得到土壤导水率与温度之间的相关关系式为

综合式（1）～（3）和式（6），降雨非饱和入渗过程中土壤热量运移的数学模型为

2.3 定解条件

根据对于降雨非饱和入渗过程中土壤热量运移数学模型的基本假定，确定式（7）数学模型的初始条件和边界条件。

初始条件如式（8）所示

式中为土壤表面至一定深度的单宽区域，范围0～，m；0()为初始时刻=0时，土壤内部与含水率相对应的负压水头分布，m；0() 为初始时刻=0时，土壤内部各点的温度，℃。

已知土壤水头和温度边界条件

式中1为已知水头边界；1为已知温度边界；1()为1边界上的已知水头分布，m；1()为1边界上的已知温度分布，℃。

土壤水流量和热流量边界条件

式中2为已知土壤水流量边界；2为已知热流量边界；()为2边界上的已知土壤水流量分布，m3；()为2边界上的已知热流量分布，W。

土壤热对流边界条件[30]

式中3为土壤自然热对流边界；为土壤表面的放热系数，W/m2·℃；T为土壤表面的气温温度，℃。

土壤降雨入渗边界：降雨后的雨水渗入到土壤之中，是自然界水循环过程中的重要环节。当降雨强度p小于土壤的入渗能力时，降雨自由入渗，没有形成地表径流，此时入渗边界条件属于第二类边界；当降雨强度p大于土壤的入渗能力时，形式降雨积水压力入渗，一部分降雨渗入土壤，一部分降雨形成地表径流，此时降雨边界条件属于第一类边界，本文暂不考虑积水入渗情况。

2.4 数值求解与程序设计

目前，对于降雨非饱和入渗过程的土壤热量运移数值计算方法主要以有限元法（Finite Element Method）、有限差分法（Finite Difference Method）为代表[1]。因此，为了揭示降雨非饱和入渗对土壤热量运移影响机理，本文采用Galerkin加权余量法（Weighed Residual Method）建立有限元方程，利用Fortran计算机语言强大的数学公式计算功能，编制降雨非饱和入渗过程中土壤热量运移的数值分析源程序，数值计算分析具体的求解步骤如下：

1）对空间域和时间域进行划分，满足计算精度的要求。

2）根据已知土壤温度边界值0(n-1)()，在不考虑降雨入渗条件下，求解t时段内土壤温度场分布0(n)(,)；

3）将已知土壤温度场分布，求解K()和D，施加降雨入渗条件，进而求解t时段内压力水头分布0(n)(,)；根据压力水头分布，求解土壤渗流速度分布0(n)(,)

4）将所得的土壤渗流速度分布0(n)(,)，求解该时间段内入渗雨水所携带的热量Δ，进而求解热传输方程，求解得到t时段末的土壤边界节点温度值0(n)()；

5）重复2）～4）步，进行迭代计算，直至满足计算精度的要求，计算终止。

3 案例计算与验证

3.1 材料与模型

为了研究高温季节降雨入渗过程中浅层土壤温度变化及热量运移，揭示降雨入渗过程对土壤温度场分布及热量运移的影响机理，选择南京市雨花台区典型土层作为数值计算分析案例的土壤材料，建立了土壤热量运移数值计算模型，如图1所示，有限元模型单元数800个，节点数861个。为了监测数值计算过程中不同深度土壤体积含水率和温度的变化，选择0.15、0.30、0.45、0.60 m深度位置作为数值监测点，具体布置如图1b所示。

3.2 计算参数与边界条件

土壤物理力学指标及热力学参数如表1所示。

降雨非饱和入渗过程的土壤热量运移数值计算模型初始边界条件分别按水分场和温度场进行设置，其中水分场上边界初始水头2.8 m，底边界固定压力水头2.0 m，降雨自由入渗边界按实际降雨强度施加；温度场上边界初始温度35 ℃，底边界固定温度20 ℃，降雨自由入渗边界按雨水与土壤热对流/热传导施加。

图1 数值计算区域及网络划分

表1 数值计算主要指标及参数取值

3.3 计算结果与分析

利用所编制的降雨入渗过程中土壤温度场分布及热量运移数值计算程序，开展有限元计算与分析，揭示降雨入渗过程中土壤温度场分布和热量运移过程。数值分析过程中，降雨强度设为45 mm/h，降雨强度小于土壤层饱和导水率，属于自由入渗。

3.3.1 表层热交换条件下土壤热量运移演化规律

土壤温度分布和变化，是土壤热状况的反映，对于土壤热量运移过程具有重要影响。高温季节的土壤地表温度较高，在天然状态下，土壤浅层温度变化主要与外界环境热量交换密切相关。为了对比揭示降雨非饱和入渗引起水分迁移对土壤温度变化及热量运移的影响，本文首先分析了不考虑降雨入渗情况下土壤表层热交换对土壤热量运移演化规律的影响。表层热交换条件下土壤温度变化如图2所示。

从图2中可以看出，外界气温从35 ℃降低到30.5 ℃历时3.5 h。随着降雨历时的增加，表层土壤与外界环境发生热量交换，土壤表层温度逐渐降低，且热量运移影响深度逐渐增加，表层温度降低至30.5 ℃时热量运移影响深度约0.2 m左右，这主要是由土壤颗粒之间热传递及土壤表层与外界环境的热对流引起的，且随着降雨历时的推移和外界温度的持续降低，土壤热量运移影响深度会持续增加，但增加速率逐渐降低。因此，可以利用该方法分析大气环境季节性变化对土壤浅层温度场的影响，进而揭示土壤浅层区域温度场的动态变化规律。

图2 表层热交换条件下土壤温度随时间的变化

3.3.2 降雨自由入渗条件下土壤水分运移规律

降雨非饱和入渗是入渗水量在土壤中交换和运移的复杂过程，且随着降雨历时的增加，不同深度的土壤基质吸力、体积含水率也随之发生变化。降雨条件下土壤基质吸力、体积含水率随降雨历时的变化如图3所示。

从图3a中可以看出，初始条件下，土壤表层基质吸力28 kPa，随深度的增加，土壤内部基质吸力呈线性递减趋势；降雨强度45 mm/h作用下，降雨全部入渗到土壤内部，湿润锋面逐步下移；随着降雨历时的增加，土壤湿润锋继续下移，当降雨历时3.5 h时，土壤湿润锋面下移了约0.8 m。降雨入渗过程改变了土壤的体积含水率分布，从图3b中可以看出，随着土壤湿润锋面的不断下移，土壤体积含水率快速增加，且随着降雨历时的增加，土壤体积含水率的增加速率逐渐降低；湿润锋过后的土壤体积含水率逐渐接近于饱和体积含水率，且随着体积含水率的持续增加，土壤的入渗能力逐渐下降，直至趋于饱和入渗率。

注：降雨强度为45 mm·h-1，下同。

Note: Rainfall intensity is 45 mm·h-1, the same below.

图3 降雨自由入渗条件下土壤基质吸力与体积含水率随时间的变化

Fig.3 Variation of soil matric suction and volume moisture content with time under the condition of free rainfall infiltration

3.3.3 考虑降雨入渗过程的土壤热量运移规律

高温季节土壤地表温度较高，而大气降雨的雨水初始温度较低，降雨入渗水分运移对土壤温度变化及热量运移产生较大影响，是影响土壤温度场变化与热量运移的主要因素。图4为利用本文编制的热量运移数值程序获得的考虑降雨入渗过程的土壤热量运移变化计算结果。

由图4可知，外界气温从35 ℃降低到30.5 ℃历时3.5 h，考虑降雨入渗情况下的土壤热量运移影响深度达到0.6 m，比不考虑降雨入渗的过程热量运移影响深度增加了约0.4 m；而且随着土壤深度的增加，降雨入渗对于土壤温度的影响逐渐降低。这主要是由于考虑降雨入渗过程的影响，土壤孔隙中低温雨水与土壤颗粒发生热量交换，改变了原有土壤温度场的分布，而且随着降雨入渗深度的持续增加，土壤温度也随之变化，降雨非饱和入渗过程对土壤温度影响呈现逐渐减弱趋势。

根据土壤模型中不同深度的关键点布置，得到如图5所示的降雨入渗条件下不同深度土壤温度随降雨历时的变化规律。从图5中可知，土壤深度0～0.3 m范围内时，其温度变化速率比较大；随着深度的增加，土壤温度变化速率逐渐降低，大约在土壤深度0.6 m左右时，土壤入渗水流的温度与周围土壤颗粒的温度相差不大时，土壤温度场基本不再发生变化。由此可以看出，降雨入渗过程不仅改变了土壤中水分运移规律、基质吸力和体积含水率的变化，而且还影响了土壤中温度场变化及热量的运移过程，因此，研究降雨入渗过程中的土壤热量运移过程，必须考虑降雨入渗过程对土壤热量传递及运移的影响。

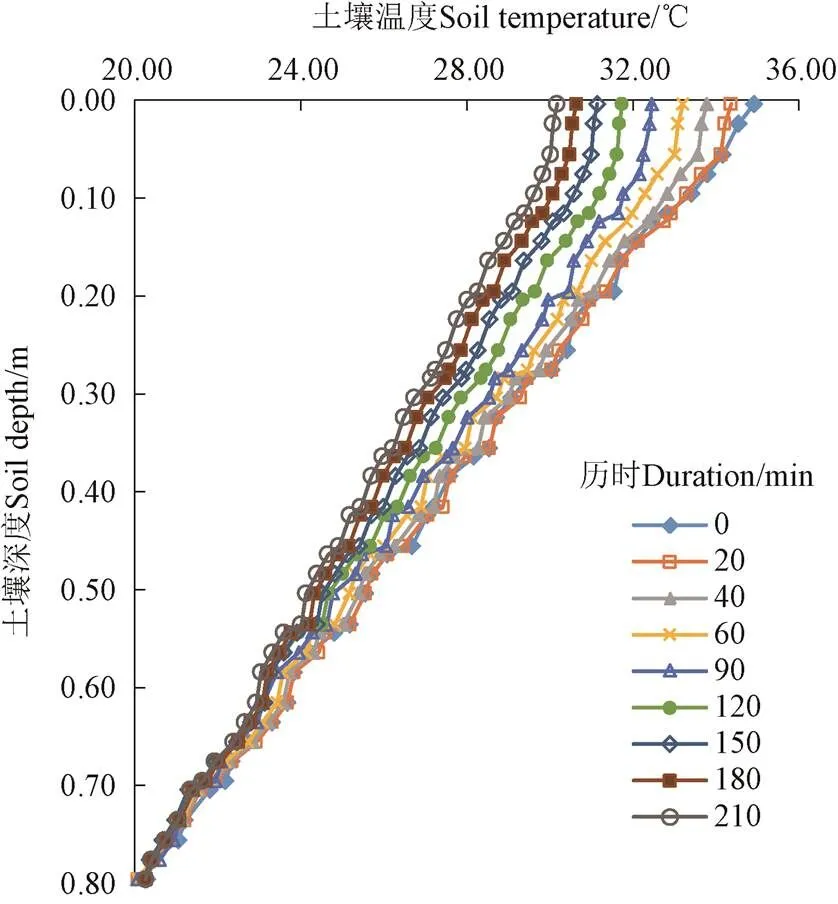
图4 考虑降雨入渗过程的土壤温度随时间的变化

图5 不同深度土壤温度随时间的变化

3.3.4 数值验证与误差分析

为了验证数值计算结果的合理性与精确性，选择南京市雨花台区典型土层进行现场测试，其具体测试流程：首先将TDR土壤水分传感器和FR-STS土壤温度传感器埋设至土壤深度0.4 m，通过数据传输线连接数据采集仪，组成现场实测数据装置如下图6所示，其中土壤体积含水率和土壤温度数据直接通过计算机自动采集，采集间隔时间为5 min。其次，降雨装置采用自动化人工控制降雨装置，降雨强度设为45 mm/h。最后，现场测试区域上边界的温度条件为外界气温，入渗边界为人工降雨自由入渗，深度0.8 m的下边界土壤温度基本保持不变。

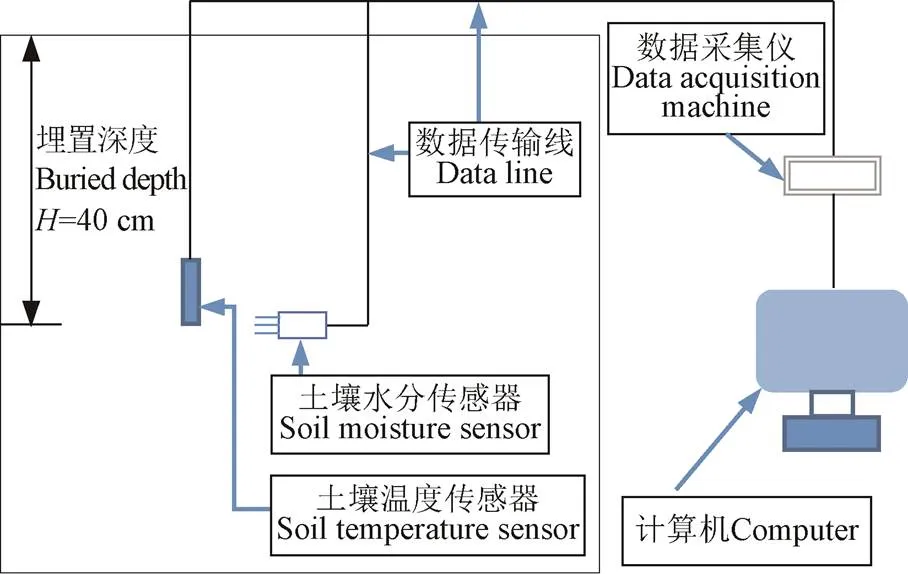
图6 土壤水热运移现场测试装置

土壤水热运移现场实测数据与数值计算结果对比分析如图7所示。从图7中可以看出，当降雨历时达到1.25 h时，降雨入渗引起的土壤湿润锋到达测点埋置深度0.4 m处，通过现场实测结果可知，所测得的土壤体积含水率呈现快速增加规律，且其增加速率先增大后减小，并逐渐趋近于稳定；通过测点埋置深度0.4 m处温度传感器测得的土壤温度从28.5 ℃逐渐降低到25.7 ℃，土壤颗粒温度传递给下渗水分，直至土壤颗粒温度与水分温度近似相同为止。

文中对土壤热量运移现场实测数据和模拟计算结果进行了综合分析与评价，并对降雨入渗过程中的土壤体积含水率、温度的实测值及模拟计算值进行了相对偏差分析（表2）。从表2可知，不同降雨历时条件下，土壤体积含水率的现场实测值和数值计算值相对偏差保持在±3.99%以内，土壤温度的现场实测值和数值计算值的相对偏差保持在±2.72%以内，说明本文提出的考虑降雨非饱和入渗过程土壤热量运移数值计算程序的合理性和适应性较好。为了进一步评价考虑降雨非饱和入渗过程的土壤热量运移计算模型的模拟计算效果，采用均方根误差（RMSE）进行精确性综合评价。从表2可知，在整个降雨非饱和入渗过程中，土壤体积含水率实测值与模拟计算值均方根误差RMSE为0.01 cm3/cm3，土壤温度实测值与模拟计算值均方根误差RMSE为0.55 ℃，可以看出误差较小，现场试验实测值与模拟计算值的整体变化规律具有较强的一致性。

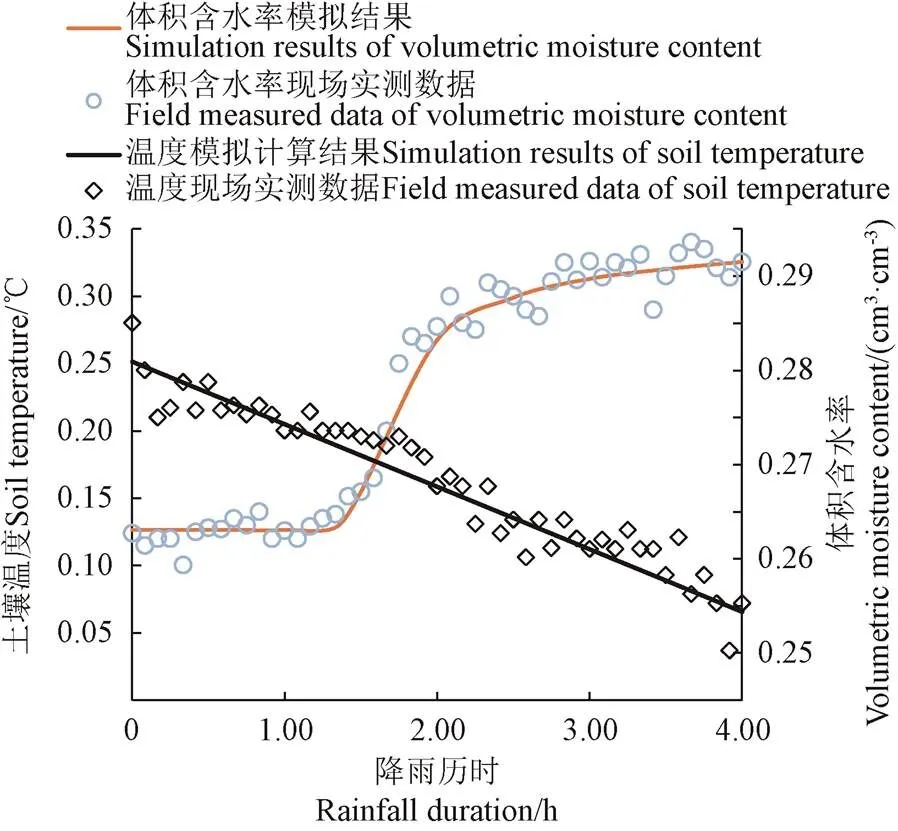
注：测点埋置深度40 cm。

表2 降雨入渗过程中土壤热量运移现场实测数据和模拟计算结果

4 讨 论

从本文数值模拟与现场实测结果可知，降雨入渗过程对土壤水热运移规律具有显著影响。本文提出的土壤热量运移数值模型特点在于既考虑了降雨非饱和入渗对土壤热量运移传输过程的影响，也考虑了土壤温度变化对土壤导水率的影响。通过与汪志荣[4]、任杰[13]和李腾风[23]提出的土壤水热运移模型对比分析发现，本研究模型可以有效揭示降雨入渗过程中土壤水热交换互馈作用及热量运移过程，现场实测结果也验证了所建立模型的合理性与实用性，研究成果对于深入研究降雨入渗引起土壤水热耦合运移机理具有重要作用与研究意义。

土壤导水率与土壤温度变化密切相关，土壤初始含水率时空差异是影响降雨入渗过程中土壤水热耦合运移数值模拟准确性的重要影响因素。龙哲[31]、白雪儿等[32]研究发现，由于土壤非均质性的影响，土壤初始含水率测试很难达到精确，而且对于土壤质地和结构所造成的土壤含水率时空差异性也无法定量给出。但是，本文提出的数值模型假定土壤视为各向同性多孔介质，没有考虑土壤质地和结构变化所造成的非均质性，以及气相影响、蒸发、溶质势和汇源项等因素，因此，本文研究模型需要进一步深入分析。

实际的降雨入渗过程一般可以分为2个阶段：第一阶段为降雨强度控制阶段，第二阶段为土壤入渗能力控制阶段，2个阶段的临界点为积水点。第一阶段入渗过程为自由入渗，第二阶段为积水入渗。通过与王帅兵等[33-34]土壤降雨入渗特性研究对比分析发现，本文提出的模型主要考虑了土壤的降雨非饱和入渗过程，即自由入渗过程，但是没有考虑坡面的积水入渗对土壤水热运移的影响。虽然张超[22]、宫兴龙[24]等学者定量研究了降雨条件下坡面薄层水流对土壤温度场分布的影响，但是并没考虑实际的降雨入渗全过程，且目前完全反映土壤降雨入渗全过程的数值模拟手段还不完善，需要开发先进的土壤水热运移数值计算程序。

5 结 论

本文建立了反映降雨入渗过程中土壤热量运移规律数学模型，开展了降雨非饱和入渗对土壤热量运移影响的数值计算与分析，得到如下结论：

1）高温季节土壤颗粒之间热传递及土壤表层与外界环境热对流是引起土壤表层温度变化的主要因素。随着降雨历时的增加，表层土壤与外界环境发生热量交换，土壤表层温度逐渐降低，且土壤热量运移影响深度逐渐增加，表层温度降低至30.5 ℃时土壤热量运移影响深度约0.2 m。

2）降雨非饱和入渗是引起土壤基质吸力、体积含水率变化的主要动力。降雨强度45 mm/h作用下，随降雨历时增加，雨水全部自由入渗到土壤内部，土壤内部基质吸力呈线性递减趋势，湿润锋面逐渐下移，土壤体积含水率快速增加；湿润锋过后的土壤体积含水率逐渐接近于饱和体积含水率，土壤入渗能力逐渐下降，直至趋于饱和入渗率。

3）土壤深度0～0.3 m范围内时，其温度变化速率比较大；随着降雨入渗深度的增加，土壤温度变化速率逐渐降低，土壤深度约0.6 m左右时，土壤温度场基本不再变化；随着湿润锋逐渐向土壤深部推进，降雨入渗过程对土壤温度影响呈现逐渐减弱趋势，考虑降雨入渗比不考虑降雨入渗的土壤热量运移影响深度增加了约0.4 m，从而揭示出降雨入渗过程对土壤热量传递及运移影响的重要作用。

4）经过现场实测数据与模拟计算结果验证，不同降雨历时条件下，土壤体积含水率现场实测值和数值计算值相对偏差保持在±3.99%以内，均方根误差RMSE为0.01 cm3/cm3；土壤温度实测值和数值计算值的相关误差保持在±2.72%以内，均方根误差RMSE为0.55 ℃，模拟计算结果和现场实测数据均吻合较好，进而验证了该模型数值计算程序的合理性与适用性。

[1]雷志栋，杨诗秀，谢森传. 土壤水动力学[M]. 北京：清华大学出版社，1988：77-81.

[2]陈军锋. 不同地表处理及潜水位下土壤水热迁移规律的试验研究[M]. 北京：中国水利水电出版社，2014：75-85.

[3]Das D, Kar B B. Impact of soil moisture and soil temperature on the physico-chemical property of laterite soil[J]. Asian Journal of Water, Environment and Pollution, 2020, 17(1): 91-96.

[4]汪志荣，张建丰，王文焰，等. 温度影响下土壤水分运动模型[J]. 水利学报，2002，35(10)：46-50. Wang Zhirong, Zhang Jianfeng, Wang Wenyan, et al. Applicability of Green-Ampt formula for infiltration affected by temperature[J]. Journal of Hydraulic Engineering, 2002, 35(10): 46-50. (in Chinese with English abstract)

[5]辛继红，高红贝，邵明安. 土壤温度对土壤水分入渗的影响[J]. 水土保持学报，2009，23(3)：219-222. Xin Jihong, Gao Hongbei, Shao Ming’an. Study of the effect of soil temperature on soil water infiltration[J]. Journal of Soil and Water Conservation, 2009, 23(3): 219-222. (in Chinese with English abstract)

[6]朱红艳，刘利华，费良军. 滴灌水温对土壤入渗和土壤温度的影响[J]. 排灌机械工程学报，2019，37(10)：902-908. Zhu Hongyan, Liu Lihua, Fei Liangjun. Effects of drip irrigation water temperature on soil infiltration and soil temperature[J]. Journal of Drainage and Irrigation Machinery Engineering, 2019, 37(10): 902-908. (in Chinese with English abstract)

[7]刘利华，费良军，朱红艳. 水温对滴灌土壤水分入渗特性的影响[J]. 排灌机械工程学报，2019，37(2)：166-173. Liu Lihua, Fei Liangjun, Zhu Hongyan．Effects of water temperature on soil water infiltration characteristics under drip irrigation[J]. Journal of Drainage and Irrigation Machinery Engineering, 2019, 37(2): 166-173．(in Chinese with English abstract)

[8]马效松，付强，徐淑琴，等. 不同冻融时期土壤水分运动参数特征分析及数值模拟[J]. 应用基础与工程科学学报，2020，28(4)：774-787. Ma Xiaosong, Fu Qiang, Xu Shuqin, et al. Analysis and simulation of soil moisture movement parameters during different freezing-thawing periods[J]. Journal of Basic Science and Engineering, 2020, 28(4): 774-787. (in Chinese with English abstract)

[9]王铁行，李宁，谢定义. 土体水热力耦合问题研究意义、现状及建议[J]. 岩土力学，2005，26(3)：488-493. Wang Tiehang, Li Ning, Xie Dingyi. Necessity and means in research on soil coupled heat-moisture-stress issues[J]. Rock and Soil Mechanics, 2005, 26(3): 488-493. (in Chinese with English abstract)

[10]冉洪伍，范继辉，黄菁. 冻融过程土壤水热力耦合作用及其模型研究进展[J]. 草业科学，2019，36(4)：991-999. Ran Hongwu, Fan Jihui, Huang Jing. Review of the coupling of water and heat in the freeze-thaw process and its model of frozen soil[J]. Pratacultural Science, 2019, 36(4): 991-999. (in Chinese with English abstract)

[11]杨荣赞，丁艳萍，刘有梅，等. 樱桃园土壤水热变化特征及其对气象因子的响应[J]. 中国农业通报， 2020，36(8)：67-72. Yang Rongzan, Ding Yanping, Liu Youmei, et al. Soil moisture and temperature in cherry orchard: Variation characteristics and response to meteorological factors[J]. Chinese Agricultural Science Bulletin, 2020, 36(8): 67-72. (in Chinese with English abstract)

[12]陈琳，费良军，傅渝亮，等. 不同土壤温度和容重下微咸水上升毛管水运动特性HYDRUS模拟及验证[J]. 水土保持学报，2018，32(6)：87-96. Chen Lin, Fei Liangjun, Fu Yuliang, et al. Simulation and verification of movement characteristics of upward capillary water flow of saline water in soils with different soil temperatures and bulk densities using HYDRUS[J]. Journal of Soil and Water Conservation, 2018, 32(6): 87-96. (in Chinese with English abstract)

[13]任杰，沈振中，杨杰，等. 基于HYDRUS模型低温水入渗下土壤水热运移模拟[J]. 干旱区研究，2016，33(2)： 246-251. Ren Jie, Shen Zhenzhong, Yang Jie, et al. Simulation of water and heat transfer in soil under low-temperature water infiltration based on the HYDRUS model[J]. Arid Zone Research, 2016, 33(2): 246-251. (in Chinese with English abstract)

[14]张明礼，温智，董建华，等. 考虑降雨作用下的气温升高对多年冻土活动层水热影响机制[J]. 岩土力学，2019，40(5)：1983-1992. Zhang Mingli, Wen Zhi, Dong Jianhua, et al. Mechanism of climate warming on thermal-moisture dynamics of active permafrost layer considering effect of rainfall[J]. Rock and Soil Mechanics, 2019, 40(5): 1983-1992. (in Chinese with English abstract)

[15]高红贝. 非恒温条件下土壤水分运动特征分析[J]. 土地开发工程研究，2017，2(3)：22-28. Gao Hongbei. Analysis of soil water movement under non-isothermal conditions[J]. Land Development and Engineering Research, 2017, 2(3): 22-28. (in Chinese with English abstract)

[16]冯宝平，陈守伦. 用BP网络预测温度对土壤水分入渗的影响[J]. 水利学报，2003，36(2)：6-8. Feng Baoping, Chen Shoulun. Effect of temperature on soil water infiltration based on back-propagation network[J]. Journal of Hydraulic Engineering, 2003, 36 (2): 6-8. (in Chinese with English abstract)

[17]张富仓，康绍忠. 土壤水分入渗的温度效应及其数学模式[J]. 中国农业大学学报，1997，2(增刊)：20-25. Zhang Fucang, Kang Shaozhong. The temperature effect of soil water infiltration and mathematical model[J]. Journal of China Agriculture University, 1997, 2(Supp.): 20-25. (in Chinese with English abstract)

[18]雷志栋，尚松浩，杨诗秀，等. 地下水浅埋条件下越冬期土壤水热迁移的数值模拟[J]. 冰川冻土，1998，20(1)：51-54. Lei Zhidong, Shang Songhao, Yang Shixiu, et al. Numerical simulation on simultaneous soil moisture and heat transfer under shallow ground water table in winter[J]. Journal of Glaciology and Geocryology, 1998, 20(1): 51-54. (in Chinese with English abstract)

[19]Barry-Macaulay D, Bouazza A, Wang B, et al. Evaluation of soil thermal conductivity models[J]. Canadian Geotechnical Journal, 2015, 52 (11), 1892-1900

[20]Gatea A, Kouzani A, Gyasi-Agyei Y, et al. Effects of solarisation on soil thermal-physical properties under different soil treatments: A review[J]. Geoderma, 2020, 363: 114137.

[21]高红贝，邵明安. 干旱区降雨过程对土壤水分与温度变化影响研究[J]. 灌溉排水学报，2011，30(1)：40-45. Gao Hongbei, Shao Ming’an. Effect of rainfall on soil water and soil temperature in arid region[J]. Journal of Irrigation and Drainage, 2011, 30(1): 40-45. (in Chinese with English abstract)

[22]张超，冯杰，刘方贵. 坡面薄层水流对土壤温度影响的数值分析[J]. 农业工程学报，2010，26(4)：64-69. Zhang Chao, Feng Jie, Liu Fanggui. Numerical analysis of influence of hill slope sheet flow on soil temperature[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2010, 26(4): 64-69. (in Chinese with English abstract)

[23]李腾风，王志良，申林方，等. 基于格子Boltzmann方法非饱和土体水热耦合模型研究[J]. 工程力学，2019，36(9)：154-160. Li Tengfeng, Wang Zhiliang, Shen Linfang, et al. A coupled moisture-heat model for unsaturated soil based on lattice Boltzmann method[J]. Engineering Mechanics, 2019, 36(9): 154-160. (in Chinese with English abstract)

[24]宫兴龙，付强，李衡，等. 薄层水流对土壤温度影响的格子Boltzmann法分析[J]. 广西大学学报：自然科学版，2014，39(4)：928-932. Gong Xinglong, Fu Qiang, Li Heng, et al. Lattice Boltzmann analysis of influence of slope sheet flow on soil temperature[J]. Journal of Guangxi University: Nat Sci Ed, 2014, 39(4): 928-932. (in Chinese with English abstract)

[25]胡国杰，赵林，李韧，等. 基于COUPMODEL模型的冻融土壤水热耦合模拟研究[J]. 地理科学，2013，33(3)： 356-362. Hu Guojie, Zhao Lin, Li Ren, et al. The water-thermal characteristics of frozen soil under freeze-thaw based on COUPMODEL[J]. Scientia Geographica Sinica, 2013，33(3): 356-362. (in Chinese with English abstract)

[26]蔡迪文，张克存，安志山，等. 积沙影响下伏冻土的水热耦合模型研究[J]. 干旱区地理，2017，40(3)：523-532. Cai Diwen, Zhang Kecun, An Zhishan, et al. Coupled hydrothermal model of underlying permafrost influenced by sand accumulation[J]. Arid Land Geography, 2017, 40(3): 523-532. (in Chinese with English abstract)

[27]张明礼，韩晓斌. 基于COMSOL Multiphysics数学模块的冻土水热耦合分析[J]. 科学技术与工程， 2018， 18(33)： 7-12. Zhang Mingli, Han Xiaobin. Analysis of coupled water and heat transfer in frozen soil based on mathematical module of COMSOL Multiphysics[J]. Science Technology and Engineering, 2018, 18(33): 7-12. (in Chinese with English abstract)

[28]Christos T, George P, Kyriakos P, et al. Fuzzy Analytical Solution to Vertical Infiltration[J]. Journal of Software Engineering and Applications, 2020, 13(4): 41-66.

[29]Constantz J, Murphy F. The temperature dependence of ponded infiltration under isothermal conditions[J]. Journal of Hydrology, 1991, 122(1-4): 119-128.

[30]刘明，章青，刘仲秋，等. 考虑渗透系数变化的地下结构温度-渗流耦合分析[J]. 力学季刊，2011，32(2)：41-46. Liu Ming, Zhang Qing, Liu Zhongqiu, et al. Study on thermo-hydro coupling model of underground structure with permeability coefficient changes[J]. Chinese Quarterly of Mechanics, 2011, 32(2): 41-46. (in Chinese with English abstract)

[31]龙哲. 土壤的初始含水率及容重对其入渗特性的影响[J]. 环境与发展，2019，31(8)：133-134. Long Zhe. Effects of initial moisture content and bulk density on soil infiltration characteristics[J]. Environment and Development, 2019, 31(8): 133-134. (in Chinese with English abstract)

[32]白雪儿，艾一丹，杨昊晟，等. 不同初始土壤含水率和滴头流量下滴灌土壤湿润体特征及其有效性评价[J]. 灌溉排水学报，2019，38(8)：73-78. Bai Xueer, Ai Yidan, Yang Haosheng, et al. Effects of different initial water content and dripper discharge on wetted body characteristic of drip irrigation[J]. Journal Of Irrigation and Drainage, 2019, 38(8): 73-78. (in Chinese with English abstract)

[33]王帅兵，王克勤，宋娅丽，等. 不同时间尺度反坡台阶红壤坡耕地土壤水分动态变化规律[J]. 农业工程学报，2019，35(8)：195-205. Wang Shuaibing, Wang Keqin, Song Yali, et al. Dynamic variation of soil moisture at different temporal scales in red soil sloping farmland under reverse-slope terrace[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(8): 195-205. (in Chinese with English abstract)

[34]刘为宗，王文海，李俊奇，等. 自然失水条件下土壤的入渗特性研究[J]. 环境工程，2020，38(4)：72-76. Liu Weizong, Wang Wenhai, Li Junqi, et al. Study on infiltration characteristics of soil under natural drying process conditions[J]. Environmental Engineering, 2020, 38(4): 72-76. (in Chinese with English abstract)

Influences of rainfall unsaturated infiltration on the change of heat transfer in soils

Zhang Chao1,2, Jiang Jingshan1, Wang Rubin3, Jin Hua1

(1.,,211167,; 2.,,211167,; 3.,,210098,)

In the high temperature season, the surface temperature of the soil is very high, and the internal moisture content of soil is low. A sudden rainfall has a great influence on the dynamic change of soil temperature, and as well as the water-heat exchange and migration. Temperature change of soil surface and water movement can be interacted with each other during this time. It is also very important to reveal the influence mechanism of water movement caused by rainfall unsaturated infiltration, on temperature change of soil and the law of heat transfer. However, there are only a few research achievements on the hydrothermal interaction of soil in the process of rainfall unsaturated infiltration. In this study, a mathematical model of soil heat transfer in the process of rainfall infiltration was established, and the corresponding finite element numerical calculation program was compiled, in order to reveal the soil moisture movement in unsaturated rainfall infiltration process of high temperature, and the influence mechanism of soil heat transfer. Taking the typical silt soil layers in Nanjing as research objects, a numerical analysis was carried out for the unsaturated rainfall infiltration exerting to the function of soil heat transfer. The results showed that without considering rainfall infiltration, the soil temperature change and heat transfer were mainly caused by the heat exchange between the surface soil and the environment, where the depth of heat transfer was about 0.2 m. Under the action of rainfall intensity of 45 mm/h, the soil matric suction and volume moisture content in the silt layer changed gradually with the duration of rainfall, due to the unsaturated infiltration process of rainfall. When the soil moisture front moves down and reached different depths, the volume moisture content increased rapidly, and the soil volume moisture content after the moist front gradually approached the saturated volume moisture content and the soil infiltration capacity gradually decreased until reaching the saturation infiltration rate. In rainfall unsaturated infiltration, the heat exchange occurred between the low-temperature rainfall in soil pores and soil particles, which can change the distribution of original temperature field in soil. Moreover, the influence of rainfall infiltration process on soil heat transfer gradually weakened, with the continuous increase in the depth of rainfall infiltration. Compared with the data of field measurement and the simulation results, the relative error of measured and calculated soil volume moisture content remained within ±3.99%, and the Root Mean Square Error (RMSE) was 0.01 cm3/cm3. The relative error of soil temperature between measured and numerical values remained within ±2.72%, and the RMSE was 0.55℃, indicating that the simulation results and the measured data were consistent with better. It infers that there was a strong adaptability in the model for the rainfall unsaturated soil infiltration process, and heat migration in soil, and the model was verified by numerical program. The causes of errors were related to the initial moisture content of the soil, the initial temperature, and the accuracy of rainfall infiltration during the test. The findings can provide an important reference for water conservancy engineering in modern agriculture, including the soil and water conservation, distribution and utilization of soil hydrology and water resources, control of urban water resources and ecological environment protection. It is of great significance to further study the coupled migration mechanism of soil water and heat transfer caused by rainfall infiltration.

soils; temperature; heat transfer; rainfall unsaturated infiltration; water movement; numerical calculation

张超，姜景山，王如宾，等. 降雨非饱和入渗对土壤热量运移变化的影响[J]. 农业工程学报，2020，36(18)：118-126.doi：10.11975/j.issn.1002-6819.2020.18.015 http://www.tcsae.org

Zhang Chao, Jiang Jingshan, Wang Rubin, et al. Influences of rainfall unsaturated infiltration on the change of heat transfer in soils[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2020, 36(18): 118-126. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2020.18.015 http://www.tcsae.org

2020-06-19

2020-09-09

国家重点研发计划（2017YFC1501104）；国家自然科学基金项目（51679069，51409082）；南京工程学院引进人才科研启动基金（YKJ201729）

张超，博士，博士后，讲师，主要从事土壤降雨入渗耦合机理等方面的研究。Email：zcnj@njit.edu.cn

10.11975/j.issn.1002-6819.2020.18.015

TU443

A

1002-6819(2020)-18-0118-09