A High-Accuracy Online Compensation Scheme for Star Sensors

Zhao Yunan,Wang Xinlong*,Cai Yuanwen,Chen Ding,Li Qunsheng

(1.School of Astronautics,Beihang University,Beijing 100191,China;2.Department of Graduate School,Space Engineering University,Beijing 101416,China;3.State Key Laboratory of Space-Ground Integrated Information Technology,Beijing 100086,China;4.School of Instrumentation Science and Opto-Electronics Engineering,Beihang University,Beijing 100191,China)

Abstract:Temperature has a significant impact on measurement accuracy of star sensors.In order to improve the accuracy of star sensors in different temperature conditions,the temperature errors of star sensors are analyzed and modeled systematically,and a high-accuracy online temperature error compensation scheme is proposed in this paper.Firstly,by analyzing the temperature influences on the optical system of star sensors,the relationships between focal length drifts,optical distortion and temperature are obtained respectively,and then a systematic temperature error model of star sensors is established.Secondly,by analyzing the charge coupling device (CCD) noise characteristics,the fluctuation relationship between star positions and temperature is given,and a random temperature error model of star sensors is established.Then,according to the characteristics of systematic and random temperature errors of star sensors,a high-accuracy online temperature error compensation scheme is proposed.In the end,by the simulated CCD star sensor,it is indicated that the proposed temperature error compensation scheme can effectively restrain the shifts and fluctuation of star positions,and then can improve the measurement accuracy of star sensors in different temperature conditions.

Key words:star sensor;temperature;systematic error;random error;online compensation

0 Introduction

The star sensor is one of the frequently-used attitude measuring devices for spacecrafts,which has advantages in autonomy and accuracy[1].However,spacecrafts work in the space with a wide temperature range from -160 ℃to 180 ℃[2],and optical systems,imaging sensors and other main components of star sensors are sensitive to temperature variations[3-4].As a result,temperature variations can directly influence the imaging quality of star sensors,and further significantly influence their accuracy.Researches show that the temperature errors are more than 50% of the total errors of star sensors[5].Therefore,how to reduce the temperature errors has become one of the key technologies for star sensors.

At present,the methods of restraining star sensor temperature errors can be categorized into two major kinds:the hardware method and the software method.For hardware aspects[6-9],the athermalisation and thermal control methods are introduced to the system design of star sensors.However,these methods need high cost and long development time.For software aspects[5，10-14],temperature error models of star sensors are established so as to compensate the errors online.These methods have characteristics of low cost and good flexibility,which have attracted the attention of military field.In literature [5],according to the temperature-dependent parameters of optical systems,the temperature effects of focal length variations on star sensor imaging accuracy can be obtained.In literature [10-11],the image shifts of star sensors are deduced by means of the lens material properties and the matrix optics theories.In literature [12],considering refractive index variations of optical systems with temperature,the relationship between emergence angle variations of stars and temperature variations can be analyzed quantitatively.Then a thermal radial distortion model of star sensors based on starlight vector calibration is established.For imaging sensors,in literature [13-14],the relationship between temperature variations and the imaging performance is described by establishing the CCD noise models.

As mentioned above,researches of temperature effects on star sensors are limited to lens distortion,image shifting and other sole and simple variation,and there is no systematic analysis and high-accuracy model of temperature errors.So these errors can not be accurately compensated online.As a result,in this paper,a comprehensive temperature error model of star sensors is established,and then a high-accuracy online compensation scheme is proposed.

1 Temperature error analysis of star sensors

CCD star sensors consist of optical systems,CCD chips,photoelectric conversion circuits,data processing circuits,baffles,etc[1].Among them,optical systems noise and CCD noise vary with temperature,which can affect star positions,as shown in Fig.1.

Fig.1 Temperature error propagation diagram of star sensor

Temperature-dependent optical systems and CCD chips have different impacts on extracted star positions.For the optical system,temperature variations will change the performance parameters and the relative positions of the lenses,and also bring about the thermal expansion of the lens barrel.As a result,it causes focal length drifts and optical distortion,leading to star position shifts in unison.The position shifts belong to systematic errors.For CCD chips,temperature variations will change the CCD noise characteristics.Consequently,it results in star position fluctuation,which belongs to random errors.

2 Temperature error modeling of star sensors

2.1 Systematic error modeling

Temperature variations cause focal length drifts and optical distortion of the optical system.Invar steel is used in the lens barrel of the star sensor,which has a low expansion coefficient,so the thermal expansion of the lens barrel is not considered.According to the image-forming principle,the corresponding star position shifts can be obtained,and the systematic errors can be modeled.

2.1.1 Errors of focal length drifts

Temperature variations can change the lens curvature,refractive index and other parameters,which lead to focal length drifts.The overall temperature coefficient of focal length driftsαfcan be expressed as[10]

(1)

whereαfiis the temperature coefficient of focal length drifts ofith lens.So the focal length drifts can be denoted as

Δf=αf·f·ΔT

(2)

According to the geometric relationship of similar triangles,the star position shifts caused by focal length drifts Δfcan be written as

(3)

where (x,y) represents the star position at calibration temperature.

2.1.2 Errors of lens distortion

Lens distortion mainly includes radial distortion and decentering distortion.Radial distortion results from the curvature and refractive index variations of the lenses.As shown in Fig.2,radial distortion varies the direction of the starlight vectorS,making the star position shift fromP(x,y) toP2(x2,y2).

Fig.2 Effect schematic of radial distortion on star positions

Radial distortion can be described by the following mathematical model[15]:

(4)

wherek1is the radial distortion coefficient,δris high-order items of radial distortion.

The radial distortion coefficientk1varies with temperature.So we can fit the relation between temperature and the distortion coefficient with polynomials,and then obtaink1at different temperatures:

k1=a0+a1(ΔT)+a2(ΔT)2+…+al(ΔT)l

(5)

wherea0～alare temperature coefficients ofk1,andlis the polynomial order.Substituting equation (5) into equation (4),we can obtain the errors of radial lens distortion(Δxr,Δyr).

Decentering distortion is caused by non-collinear optical axes of the lenses in the optical system.As shown in Fig.3,decentering distortion varies the direction of the starlight vectorS,making the star position shift fromP(x,y) toP3(x3,y3).

Fig.3 Effect schematic of decentering distortion on

star positions

Decentering distortion can be described by the following mathematical model[15]:

(6)

wherep1andp2are the decentering distortion coefficients,δdis high-order items.

Similarly to radial distortion,the decentering distortion coefficientsp1andp2can be obtained by polynomial fitting:

p1=b0+b1(ΔT)+b2(ΔT)2+…+bm(ΔT)m

p2=c0+c1(ΔT)+c2(ΔT)2+…+cn(ΔT)n

(7)

whereb0～bmandc0～cnare temperature coefficients,mandnare the polynomial orders.Substituting equation (7) into equation (6),the position errors of decentering distortion (Δxd,Δyd) can be obtained.

2.1.3 Systematic temperature error model

Temperature variations can lead to focal length drifts and optical distortion.These two factors can result in star position shifts together,as shown in Fig.4.

Fig.4 Effects of focal length drifts and lens distortion on star positions

Based on the relationship between the temperature variations,focal length drifts and optical distortion,the systematic temperature errors can be derived by integrating equations (3)～(4) and equation(6):

(8)

where(xi,yi)is the star position at calibration temperature.

Equation (8) describes the relationship between temperature variations ΔTand the star position shifts (Δxs,Δys),called the systematic error model.

2.2 Random error modeling

Temperature variations change the CCD noise characteristics,which will reduce the image quality of star maps and the star centroiding accuracy.CCD noises mainly include photon shot noise,photo response non-uniformity noise,dark current shot noise,dark signal non-uniformity noise and readout noise[13].Among them,dark current noise and readout noise are influenced by temperature remarkably.

2.2.1 Temperature effects upon CCD noises

(1) Dark current noise

CCD dark current is generated by irregular thermal motion of semiconductor carriers,which is usually specified as the number of thermal electrons per second.Dark currentIis affected by temperature significantly and can be given as a function of absolute temperatureT[16]:

(9)

wherekis the Boltzmann’s constant,E(T) is the band-gap energy of silicon.

Since the thermal motion of carriers is a random process,dark current varies in different time and different pixels.It forms dark current shot noise and dark signal non-uniformity noise.

Dark current shot noise is equal to the square root of dark signal generated during the exposure timet[16].Combined with equation (9),dark current shot noiseσdcsnin electrons can be obtained:

(10)

whereNdsis dark signal in electrons，andcis a constant.According to equation (10),the higher the temperature is,the more obvious the dark current shot noiseσdcsnwill be.

Due to the differences in the fabrication process of CCD chips,dark current is often not evenly distributed on each pixel[16].Dark signal non-uniformity noise shows the non-uniformity of dark signal in different pixels,which is a kind of spatial noise.

The dark signal non-uniformity noise increases in the same proportion as the dark signal.The dark signal non-uniformity noiseσdsnuin electrons can be calculated by dark signal non-uniformity voltageUdsnu0at room temperatureT0:

(11)

whereSvis the CCD output stage sensitivity in volts/electrons,andUdsnu0is usually provided by the manufacturer.Similarly,dark signal non-uniformity noiseσdsnushows more obviously when temperature is higher.

(2) Readout noise

Readout noise consists of reset noise and output amplifier noise.Reset noiseσresetis mainly caused by the thermal noise of reset resistors in CCD output stage,which can be expressed as[13]

(12)

whereCrepresents the sense node capacitance,andqis the fundamental charge.It is easy to find that the reset noise increases with temperature increment.

In addition to reset circuits,the readout circuits contain output amplifier circuits,which can lead to flicker noise and white noise.Flicker noise is dependent on frequency instead of temperature.White noise has nothing to do with frequency but with temperature[13],which can be written as

(13)

whereBis the noise power bandwidth,Routis the output resistance.White noise in output amplifier circuits also increases with temperature increment.

Therefore,temperature-dependent CCD noisesσTconsist of dark current shot noise,dark signal non-uniformity noise,reset noise and white noise of readout noise,which can be written as:

(14)

According to equations (9)～(14),it is easy to find that CCD noises are more and more conspicuous with the increase of temperature.

2.2.2 Temperature effects upon CCD noises

According to the temperature characteristics of CCD dark current noise,the star position fluctuation caused by temperature variations can be derived.The measurement signalUijof the star map is composed of the original signalSijand the noise signalNij.According to the star centroiding algorithm[17],the random error of the star position inxdirection can be derived by

(15)

wherexis the star position extracted from the star map,x0is the ideal star position.

It is easy to see that sum of the noises is much smaller than sum of the signals.Considering the effects of temperature-dependent CCD noisesσTin chief,the variance of Δxucan be approximated as

(16)

wherex0obeys the uniform distribution within the pixel interval of [-0.5,0.5],n=(m-1)/2 andmis the pixel size of star spots.Similarly,the variance of the random errors inydirection can be procured.Equation (16) measures the relationship between temperature and the fluctuation range of the star positions,i.e.statistical characteristic of random errors.

Equations (8) and (16) measure the star position shifts and fluctuation caused by temperature variations respectively,which are the systematic error model and random error model of star sensors.According to the position shifts and fluctuation range of multiple stars at different temperatures,the attitude at corresponding temperature can be calculated,and the attitude errors can be obtained compared with the ideal attitude information.

3 A high-accuracy online temperature error compensation scheme for star sensors

3.1 Design of temperature error compensation scheme for star sensors

According to the characteristics of systematic error and random temperature error of star sensors,a high-accuracy online temperature error compensation scheme is designed,as shown in Fig.5.It includes two aspects:the calibration of temperature error models and the temperature error compensation.

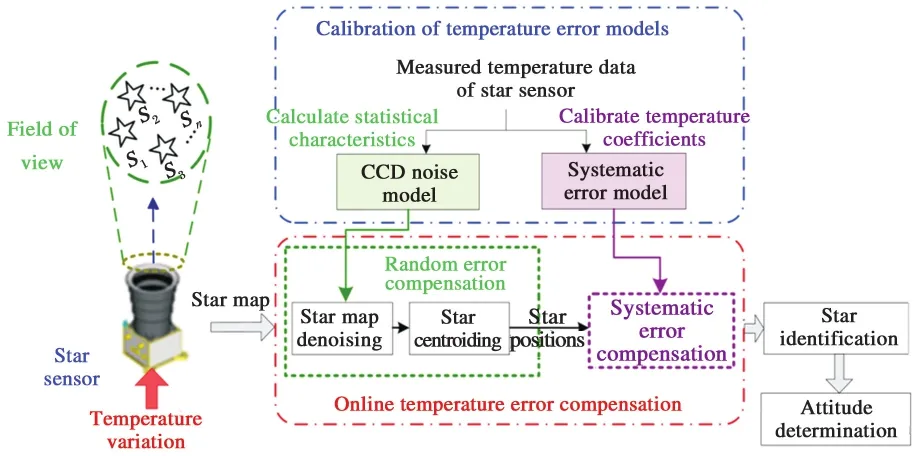
Fig.5 Block diagram of the online temperature error compensation scheme

The calibration of temperature error models is the basis of online compensation.By using the ground test data of the star sensor,the CCD noise model can be established and the temperature coefficients of the systematic error model can be calibrated.

The online temperature error compensation consists of two parts:random error compensation and systematic error compensation.Based on the CCD noise model,the star maps can be denoised so as to extract more accurate star positions.Then the star position shifts can be corrected with the systematic temperature error model.

3.2 Compensation methods of temperature errors

3.2.1 Compensation method of systematic errors

(17)

(2) CalculateXusing the iteration formula.

The iteration formula is

Y(k+1)=Y(k)-[F′(Y)]-1F(Y)

(18)

whereY(k)is the iteration star position at timek,andF′(Y)is the Jacobian matrices ofF(Y):

Its elements are

(3) If |Y(k+1)-Y(k)|<ε,the iteration is over andY(k+1) is the compensated star position.Otherwise,setY(k+1) as the iterative initial value and return to step (2).In this way,the compensated star position can be obtained from the star position at different temperatures.

3.2.2 The compensation method of random errors

In view of the uncertainty of random temperature errors,it is difficult to reduce them exactly.Consequently,they can be compensated indirectly by suppressing temperature-dependent CCD noises of star maps.

(19)

whereG(u,v),H(u,v) andP(u,v) denote the discrete Fourier transform (DFT) ofg(i,j),h(x,y) andp(x,y) respectively.h(x,y) is the point spread function (PSF) of the degradation model,p(x,y) is the second-order difference Laplacian operator.γcan be determined according to the characteristics of star map noises by iteration.

In the temperature error compensation of star sensors,we use the constrained least squares filter to suppress the star map noise firstly,which can reduce the star position fluctuation.Afterwards,based on the calibrated systematic error model,we use the Newton iteration method to obtain the final compensation results.

4 Simulation and verification

4.1 Simulation conditions

The performance of the simulated star sensor is shown in Table 1.The star maps taken by the simulated star sensor contain background noises with variance 8 gray values and temperature-dependent noises with variance 0.5×1.15ΔTgray values.The calibration temperature is 25 ℃,the temperature variations are from -20 ℃ to 20 ℃.

Table 1 Performance parameters of the CCD star sensor

When analyzing temperature errors of the star sensor,the optical axis direction (α0,β0) is set as (50°,30°).Four bright starsSa～Sdlocated in four quadrants of the field of view (FOV) are selected as illustrations shown in Fig.6.Their distances from the center of the FOV satisfyrb>ra>rd>rc.

Fig.6 Distribution of the four stars selected as illustrations

4.2 Comparison of star positions before and after the compensation

The star positions ofSa～Sdcan be extracted from the star maps taken by the star sensor at different temperatures.Compensated star positions can be obtained by using the proposed compensation scheme.Fig.7～10 respectively show the star position errors ofSa～Sdinxandydirections before and after the compensation.

Fig.7 The star position errors of Sa varied with temperature

Fig.8 The star position errors of Sb varied with temperature

According to the solid lines in Fig.7～10,when thex-coordinate of the star is greater than 0(Sa andSd),Δxwill increase continuously with temperature increment.When thex-coordinate is less than 0(SbandSc),the law of Δxis opposite.Similarly,the law of they-coordinate is uniform with that of thex-coordinate.It can be seen clearly when the temperature variation is greater,the star position errors are more appreciable.Furthermore,if the temperature is higher than the calibration temperature,the star spots deviate from the center of the image plane.In addition,these figures also verify that identical temperature variation has different effects on different stars.Analyzing the relation between the star position errors and their distancer,if stars are farther away from the center of the FOV,their positions are affected by temperature more obviously.The direction deviation is larger depending on the star position on the image plane.

Fig.9 The star position errors of Sc varied with temperature

Fig.10 The star position errors of Sd varied with temperature

According to the dotted lines in Fig.7～10,via the compensation of the systematic and random errors,the star position errors ofSa～Sdare stable within 0.2 pixels and independent of temperature.It indicates that the compensation scheme is applicable to all the stars in the FOV,and it can provide high-accuracy star positions for the follow-up star identification and attitude determination.

4.3 Comparison of attitude estimates before and after the compensation

In order to measure the temperature effects on attitude accuracy of star sensors,star maps are taken at each temperature by 100 Monte Carlo tests,and the star positions are obtained.After star identification,the optical axis direction (α0,β0)can be calculated.Then the star positions are corrected by the proposed compensation scheme,and the attitude after compensation can be obtained as well.Table 2 shows the root mean square error of the attitude before and after the temperature error compensation.

Table 2 The comparison of attitude accuracy before and after compensation

According to the left part of Table 2,it can be seen that at calibration temperature (when ΔTis 0 ℃),the attitude errors of the star sensor are within 0.001°.However,with the increase of the temperature variation ΔT,the attitude errors increase continuously.Especially,when the temperature variation ΔTreaches 15 ℃ or higher,the optical axis direction errors are above 0.1°,which cannot meet the actual accuracy requirements of star sensors obviously.According to the right part,it is clear that by compensating the temperature errors of star positions,the temperature effects on attitude accuracy can be suppressed.The attitude errors are stabilized within 0.002°,which are reduced by 1～2 orders of magnitude compared with errors before compensation.It demonstrates that the proposed compensation scheme can improve the measurement accuracy of star sensors greatly.

5 Conclusions

Temperature variations can greatly reduce the measurement accuracy of star sensors.In this paper,by analyzing the temperature error characteristics of star sensors,a comprehensive temperature error model is established,and a high-accuracy online temperature error compensation scheme is proposed.The following conclusions are obtained.

For the optical system of star sensors,temperature variations can change the refractive index,the radius of curvature and other parameters of the lenses,which generates focal length drifts and radial distortion.Temperature variations can also change the coaxiality of the lenses and can bring about thermal expansion of the lens barrel,which causes decentering distortion.These factors result in the star position shifts jointly,namely systematic errors.For CCD chips,CCD noises increase significantly with temperature increment.It causes variations of star map noises,resulting in star position fluctuation,namely random errors.

The established temperature models of star sensors in this paper contain the effects of focal length drifts,optical distortion and CCD noises.The proposed online temperature error compensation scheme is simple to be implemented and suitable for online compensation.It can guarantee the measurement accuracy of star sensors at different temperatures.In future studies,performance of the proposed online temperature error compensation scheme for star sensors should be further verified by combining the measured data obtained by the star sensor in engineering applications.