基于可靠性的阵列天线幅相容差优化方法
2020-12-03周强锋赵志江
周强锋,赵志江
(1.中国空空导弹研究院,河南 洛阳 471009;2.航空制导武器航空科技重点实验室,河南 洛阳 471009;3.陆装航空军事代表局,北京 100036)
0 引 言
低/超低副瓣阵列天线己经成为高性能雷达系统的一个重要组成部分,能够提高整个雷达系统的抗干扰性能[1-3]。阵列天线研制中受天线加工、安装和馈电误差等影响,存在不同来源的随机误差,影响阵列天线单元激励幅度和相位,引起幅相误差。幅相误差会导致天线副瓣电平恶化、抗干扰能力下降,甚至使得阵列天线功能失效。正确分析和设计天线容差已成为阵列天线设计过程中的关键环节和重要研究内容。
在阵列天线容差研究中,常用方法是假设误差服从某种分布,采用概率统计理论推导获得误差与阵列性能的影响关系[4]。基于误差服从正态分布,Allen[5]研究了阵列单元幅相误差对天线方向图的副瓣电平、增益和波束指向等平均性能影响的一些统计规律公式。Hsiao[6]理论上分析获得了实现预期的平均副瓣与幅相误差之间关系的通用设计曲线。杨莘元[7]和崔金辉[8]在考虑阵列天线间互耦的条件下,研究了幅相误差引起超低旁瓣阵列天线旁瓣最高电平分布,给出了八元线阵的幅度误差、相位误差对超低副瓣阵列天线副瓣最高电平影响的关系曲线图。高坤等[9]研究了存在幅相误差下的阵列副瓣区副瓣电平的统计特性,并由此分析在整个副瓣区域内最高副瓣电平的统计特性。姚天宾等[10]理论推导和仿真分析了幅相误差对有源相控阵天线副瓣电平的影响,获得了所需副瓣电平的幅相误差分配方法。以上基于概念统计理论的阵列误差分析方法,在工程应用中只限于误差分布明确下,确定所需副瓣电平的幅相误差分布的方差。在现代雷达系统设计中更关注幅相容差设计与优化问题,增强天线系统设计高稳定性的同时,尽量放宽幅相容差范围,降低整个雷达系统的研制难度和研制成本。
为了在满足阵列天线性能要求和高可靠性的同时,尽可能获得最优的幅相容差范围,降低系统研制难度和研制成本,本文构建基于可靠性的阵列幅相容差优化数学模型,结合蒙特卡洛方法、进退法和二分法的传统迭代搜索技术,提出一种快速的阵列天线幅相容差设计优化算法,实现给定任意容差设计初始值,快速优化获得满足性能指标要求的最大容差范围。
1 数学模型
1.1 阵列天线性能可靠性分析模型
假定阵列天线单元方向图为各向同性,对于一个N元等间距排列的线阵,其天线方向图可表示为

(1)
式中:In是第n个天线单元的理想激励幅度;λ是波长;d是天线单元排列间距;θ是场空间角;θ0是波束扫描角。
阵列天线误差来源很多,包括天线单元的安装误差、天线单元失效等,表现为阵列天线激励幅度和相位误差。考虑阵列幅相误差时的天线方向图可表示为
(2)
Jn=(1+εn)Inexp(jμn)
(3)
式中:εn,μn分别是第n个单元的幅度误差和相位误差。
幅相误差的存在使得阵列天线的副瓣电平恶化,抗干扰能力下降。在固定容差范围下,当阵列单元的幅度误差εn和相位误差μn分别是[-δ,δ]和[-φ,φ]的随机变量时,阵列天线的最高副瓣电平可表示为
Fδ,φ(X)=f(ε1,…,εN,μ1,…,μN)
(4)
式中:Fδ,φ(Xi)是固定容差范围内产生的幅相误差对应的最高副瓣电平,X=(ε1,…,εN,μ1,…,μN),n=1,2,…,N。
阵列天线系统最高副瓣性能的可靠度,表示为规定的条件下和规定的时间内形成的辐射方向图最高副瓣电平不大于规定性能的概率,即
p=P(Fδ,φ(X)≤RT)
(5)
式中:RT是最高副瓣电平的设计指标;p越大,表示阵列天线系统最高副瓣性能的可靠度越高,抗干扰能力相对更强。
1.2 阵列幅相容差优化设计数学模型
实际工程中,通常希望寻找满足天线性能要求下的最大容差范围,实现合理的阵列天线容差设计,进一步降低研制难度和研制成本。
在设计阵列幅相容差范围时,两者容差设计是相互制约的,即各自容差范围不能同时取最大值,进行幅相容差优化设计时,可通过固定幅度或相位其中一个容差范围,求取另一个容差的最大值,通过多种组合优化,获得满足要求容差设计。不失一般性,以固定幅度容差范围进行相位容差的最大范围优化为例,基于阵列天线性能可靠性要求,其幅相容差优化设计问题可以看作一个带约束条件的优化问题。
φmax=maxφ
(6)
s.t.p=P(Fδ,φ(X)≤RT)≥pT;δ=δ0
式中:δ0是固定幅度容差范围的边界;pT是阵列天线最高副瓣性能可靠度设计指标。通过对式(6)进行优化计算,即可保证阵列天线最高副瓣性能可靠性度不小于pT的约束下,求解出满足性能指标要求的相位容差的最大范围φmax。
2 阵列天线容差设计优化算法
2.1 优化算法的总体描述
对于固定幅度或相位容差范围,阵列幅相容差优化设计属于一维优化问题,式(6)通过给定一个相位容差初始值,利用迭代优化算法,不断调整相位容差范围,优化求解出满足性能指标要求的相位容差最大值。
为提高容差设计优化效率,本文构造一种进退法与二分法相结合的容差设计优化算法。首先利用进退法确定相对小的搜索区间范围,再利用二分法在搜索区间内进行迭代,优化出容差设计最大值。由于阵列天线最高副瓣电平一般与幅相容差设计参数δ和φ不构成解析式,在每次迭代过程中,采用蒙特卡洛方法求解固定幅相容差范围下最高副瓣性能的可靠度。
2.2 阵列性能可靠性分析的蒙特卡洛方法
对于固定幅相容差范围下阵列天线最高副瓣性能的可靠度分析,采用蒙特卡洛方法求解过程如下:
(1) 随机产生M个2N维且每个分量都在[0,1]间的随机数向量Zi=(z1,z2,…,z2n),利用式(7)将Zi的各个分量映射到优化变量的取值范围,形成固定幅相容差范围内M个随机抽样样本Xi=(x1,x2,…,x2n) = (ε1,…,εn,μ1,…,μn),i=1,2,…,M。
(7)
(2) 计算每个样本Xi对应的阵列天线方向图的最高副瓣电平性能Fδ,φ(Xi),i=1,2,…,M。
(3) 统计计算固定幅相容差范围对应的最高副瓣电平可靠度p,即
(8)
式中:TR是样本对应的最高副瓣电平不大于设计指标RT的次数。
2.3 阵列天线幅相容差优化设计算法
在基于阵列性能可靠性分析的蒙特卡洛方法的基础上,采用进退法与二分法相相结合的阵列天线容差设计优化算法,具体步骤如下:
(1) 初始化算法参数:性能指标RT和pT,幅度容差设计参数δ=δ0,相位容差设计参数初始值φ=φ0,相位容差计算精度要求η,蒙特卡洛方法模拟样本数M,进退法循环次数m=0,二分法循环次数q=0。
(2) 利用蒙特卡洛方法计算初始条件下最高副瓣电平可靠度p,并计算下一步容差范围调整方向标识T0:
其中c=2(算法1的第4点说明).因此由文献[23]的定义3可知,′(eu,i)是2-Lipschitz[24],再由其中的定理4可得结论.该推论说明了当样本个数大于某一取值时,经目标函数加扰策略求解的结果与无差分隐私处理的结果相差的量化程度.
(9)
式中:T0=1表示已能够确定搜索区间的上界,下一步减小φ找到搜索区间的下界;T0=-1表示已找到搜索区间的下界,下一步增大φ找到搜索区间的上界。
(3) 采用进退法调整φ的取值:
(10)
式中:φm是进退法第m次调整的值。
(4) 利用蒙特卡洛方法计算调整后的p,并计算下一步调整方向标识Tm:
(11)
(5) 判定是否继续利用进退法确定搜索区间,若Tm=Tm-1,则转步骤(3);否则,确定二分法初始搜索区间[a,b]:
(12)
(6) 采用二分法在区间[a,b]进行求解,设第q次循环φq=(a+b)/2,利用蒙特卡洛方法计算p。
根据优化算法流程,阵列天线幅相容差优化设计算法计算量主要集中利用蒙特卡洛方法计算p。算法复杂度是由阵列天线规模N(阵列单元数)和蒙特卡洛方法中样本数量M决定的,即算法复杂度为O(MN)。
3 实验结果
为了验证方法的有效性,以半波长等间距排列的200元线阵为例,选择线性Taylor综合方法来设计副瓣电平不高于-40 dB的理想方向图。以最高副瓣电平不超过-30 dB为设计指标,分别对可靠度不小于95%和100%进行幅相容差设计与优化分析。仿真中,样本数M=10 000,相位容差求解精度η=0.01°。
表1给出了四种组合情况的相位容差设计优化结果。图1~2给出了在固定幅度容差范围分别为[-0.05,0.05]和[-0.1,0.1]下构成的四种组合情况的相位容差设计优化迭代过程,和最终求解的容差结果对应的最高副瓣电平可靠度分析。图3给出了四种幅相容差优化组合情况下对应的辐射方向图。从迭代过程和结果分析可知,采用本文方法迭代13次可快速求解得到相应的相位容差最大值。pT=95%,δ0=0.05对应的相位容差最大值为9.897 6°;pT=95%,δ0=0.10对应的相位容差最大值为8.481 4°;pT=100%,δ0=0.05对应的相位容差最大值为6.389 3°;pT=100%,δ0=0.10对应的相位容差最大值为3.603 5°。同等的可靠度要求下,固定的幅度容差越大,相位容差越小。同等的固定幅度容差下,可靠度要求越高,相位容差越小。

表1 四种组合情况下相位容差优化结果Table 1 The optimization results of phase tolerance for four combinations

图1 四种组合情况下相位容差优化迭代过程Fig.1 The process of phase tolerance optimization for four combinations
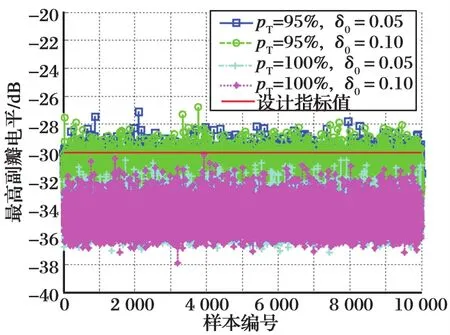
图2 四种组合情况下对应的最高副瓣电平可靠度分析Fig.2 The reliability analysis of maximum sidelobe level for four combinations

图3 四种组合情况下对应的辐射方向图Fig.3 The radiation pattern for four combinations
为了进一步分析本文方法对阵列天线幅相容差优化设计的稳健性,对组合1和组合2各进行10次独立仿真,分析结果如表2所示。
通过表2可以看出,本文方法用于阵列天线幅相容差设计优化时,多次独立求解的最大值与最小值接近,偏差较小 (体现在标准方差上),算法稳健有效。

表2 本文方法稳健性分析Table 2 The stability analysis of the proposed method
4 结 论
本文在建立阵列天线幅相容差优化模型的基础上,给出了一种融合进退法和二分法技术的阵列天线容差设计快速优化算法,适用于对给定天线性能指标和可靠度约束下,在固定幅度或相位其中一个容差范围时,获得另一个容差的最大域。本文方法可以不考虑误差分布形式,算法实现简单,具备良好的工程应用性。通过采用该方法可求解多种优化组合,在满足性能指标要求的最大幅相容差范围,实现增强天线系统设计高稳定性的同时,尽量放宽幅相容差范围,降低整个雷达系统的研制难度和研制成本。
