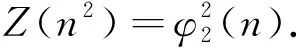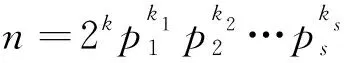数论函数方程解的探讨

梁晓艳, 高丽, 高倩

(延安大学 数学与计算机科学学院,陕西 延安 716000)

1 相关引理

引理1[7]对任意素数p≥3,Z(p)=p-1.

引理2[7]对任意素数p≥3及k∈N,Z(pk)=pk-1.当p=2时,有Z(2k)=2k+1-1.

引理3[7]Z(n)是不可加的,即Z(m+n)不恒等于Z(m)+Z(n);Z(n)是不可乘的,即Z(mn)不恒等于Z(m)Z(n).

引理4[8]Euler函数是积性函数,对于任意互素的正整数m和n,φ(mn)=φ(m)φ(n).

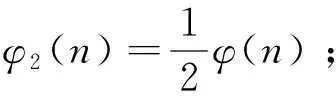
引理7[8]对于k∈Z+及素数p,有φ(pk)=pk-pk-1.

2 定理及证明

定理1对于正整数n,方程Z(n2)=φ2(n)仅有正整数解n=1.

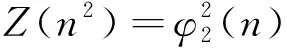
2.1 定理1的证明

证明当n为奇数时,分为以下几种情况:

(1)n=1时,Z(1)=1,φ2(1)=1,Z(1)=φ2(1),所以n=1是方程的解.

(2)n=p时,p为素数,且p≥3,则由引理1得Z(p2)=p2-1,由引理7得φ2(p)=(p-1)2,令p2-1=(p-1)2，解得p=1，与p≥3矛盾，即Z(p2)≠φ2(p),所以n=p不是方程的解.

整理得

p12p22…ps2|(p1-1)2(p2-1)2…(ps-1)2

当n为偶数时,分为以下几种情况:

(1)n=2k,其中k>0,由引理2得Z(22k)=22k+1-1,由引理7得

φ2(n)=φ2(2k)=22k-2

显然Z(n2)≠φ2(n),所以n=2k不是方程的解.

(2)n=2kpl,其中k>0,p为素数,l≥1,由引理4和引理7得

φ2(n)=φ2(2kpl)=φ2(2k)φ2(pl)=22k-2p2l-2(p-1)2

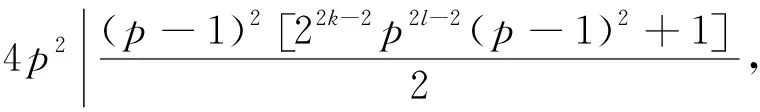
综上所述,方程Z(n2)=φ2(n)的正整数解为n=1.

2.2 定理2的证明

证明当n为奇数时,分为以下几种情况：

(1)n=1时,

所以n=1不是方程的解.

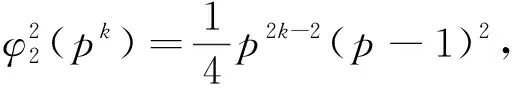
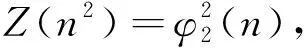
整理得

当n为偶数时,分为以下几种情况:

(2)n=2kpl,其中k>0,p为素数,l≥1,由引理5和引理7得