旋磁光子晶体单向表面模式的高效数值计算

任莹蓉， 胡真

(河海大学 理学院，江苏 南京 211100)

光子晶体[1]是一种以光波的波长尺度为周期的新型人造周期性材料,其最显著的特征是具有光子带隙.频率落在光子带隙内的光波不能在光子晶体中传播,这使得光子晶体具有了控制光的能力,被广泛应用于高辐射超小型激光器[2]、高光电转化率光伏电池[3]和量子信息元件[4]等诸多领域.

光子晶体表面模式[1]是指在光子晶体的边界面上所形成的表面波,它能够在边界面上传播,在垂直于边界面的方向上指数衰减.对于传统的各向同性光子晶体,表面模式总是成对出现,即在同一频率下,既存在正向传播的表面模式,也存在反向传播的表面模式,故光波在边界面上既能正向传播也能反向传播.旋磁光子晶体由在各个方向上磁导率不同的旋磁各向异性材料制成.人们发现在外加磁场的作用下,旋磁光子晶体因其破坏了时间反演对称性,从而能够存在单向表面模式[5-6],即在一个频率下,只存在沿着一个方向传播的表面模式,故光波在边界面上只能沿着一个方向传播,当边界面位于旋磁光子晶体与各向同性光子晶体或两种不同旋磁光子晶体的交界处时,即使结构存在缺陷,光波也不能反向散射,传输率仍然能够达到100%,整个结构是鲁棒的.基于这些优点,Chen等人设计了无损耗单向波导[6]; Zhang等人设计了高精度环形谐振器[7]; Ren等人设计了无反射三端口通道降频滤波器[8].

分析与计算光子晶体表面模式需要有效的数值方法.现有的数值方法包括有限元法[7-8]、平面波展开法[9]、传输矩阵法[10]、散射算子方法[11]等；有限元法和平面波展开法均需要离散计算区域内部,因此涉及的矩阵不容易求解,且对于色散介质,建立的是复杂的非线性特征值问题;传输矩阵法存在数值不稳定性；散射算子方法的计算则比较困难.

近年来,Lu等[12]提出了一种新的频率域数值方法,即Dirichlet-to-Neumann(DtN)映射方法.DtN映射本质上是将单元晶格边界上的波动场映射成波动场的法向导数,从而能够避免对计算区域内部进行离散,极大地减少了计算量.DtN映射方法已经被用于分析各类光子晶体结构[13-18],但从未被用于旋磁光子晶体单向表面模式的分析与计算.

本文将DtN映射方法用于计算旋磁光子晶体的单向表面模式，首先挑选出合适的超级晶格,即结构的一个周期,然后构造出超级晶格的DtN映射,最后在超级晶格的边界上建立起线性特征值问题来进行求解.

1 控制方程

为方便讨论仅考虑z方向上不变的二维结构[12-18]，图1所示的结构为一种由旋磁光子晶体(右半部分)和各向同性光子晶体(左半部分)组成的二维结构,单向表面模式存在于这两种光子晶体的交界面处.

图1 由旋磁光子晶体(蓝)和各向同性光子晶体(绿)组成的二维结构

(1)

其中u是电场的z分量,n(x,y)是折射率函数,k0是自由空间波数.

对于各向同性光子晶体,磁导率μ=μ0是一个常数,E-极化下的控制方程为Helmholtz方程

(2)

2 单元晶格的DtN映射

图1的二维结构中,旋磁光子晶体和各向同性光子晶体均由正方形周期排列的介质柱组成,其中各向同性光子晶体旋转了45°后放置在旋磁光子晶体左侧.图1中绿色实线和红色实线围成的区域即为挑选出的超级晶格,它包含三种不同的单元晶格,如图2所示.

为了构造超级晶格的DtN映射,首先需要构造出单元晶格的DtN映射.单元晶格的DtN映射Λ将边界Γ上的波动场u映射成边界上波动场u的法向导数,即:

(3)

其中ν是边界Γ上的单位法向量.

(a) 旋磁各向异性单元晶格(正方形) (b) 各向同性单元晶格(五边形) (c) 各向同性单元晶格(正方形)

对于只包含一个半径为a的介质柱的单元晶格,方程(1)和(2)的通解u可由特解的线性组合表出:

(4)

(5)

(6)

如果在单元晶格的边界Γ上离散p个点,则可以用p个特解的线性组合来近似方程(1)和(2)的通解u,然后利用(4)中的通解u及其法向导数∂νu的表达式消去未知系数cj.最终,可以用一个p×p矩阵来近似DtN映射Λ.

3 超级晶格的DtN映射和特征值问题

在得到三种单元晶格的DtN映射后,可以构造出超级晶格的DtN映射M:

(7)

构造的基本思想[16-17]是利用超级晶格内部的公共边上波动场法向导数的连续性,在公共边上建立起线性方程组,从而消去公共边上的波动场,最终得到超级晶格的DtN映射M.

为了便于叙述超级晶格的DtN映射M的构造过程,需要引入一些记号:如图3所示,将2m+1个单元晶格(从右到左)依次记为Ω(i)(i=1,2,...,2m+1),用u0,i(i=1,2,...,2m+1)表示底边界Q0Q1,…,Q2mQ2m+1的波动场u,用u1,i(i=1,2,...,2m+1)表示上边界P0P1,…,P2mP2m+1的波动场u,用wi(i=1,2,...,2m)表示公共边(虚线)的波动场u,则u0=[u0,1,...,u0,2m+1]T,u1=[u1,1,...,u1,2m+1]T,w=[w1,...,w2m]T.

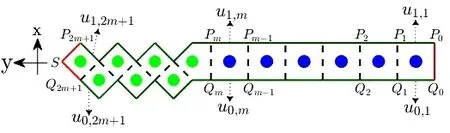
图3 由2m+1个单元晶格组成的超级晶格(m是偶数)

在超级晶格左右两边红色边界(边SP2m+1,SQ2m+1,P0Q0)处采用零边界条件,即波动场u=0.这是因为问题的计算是在光子带隙内进行,频率落在光子带隙内的光波不能在光子晶体内传播,故当左右红色边界远离两种光子晶体的交界处时,波动场快速衰减到0.

以图4所示的单元晶格Ω(m)和Ω(m+1)之间的公共边PmQm为例在超级晶格内的公共边上建立线性方程组.

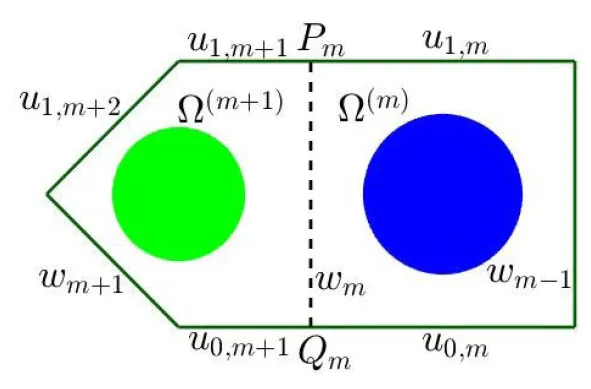
图4 单元晶格Ω(m)与Ω(m+1)的公共边

对单元晶格Ω(m)和Ω(m+1)的DtN映射Λ(m)和Λ(m+1)分别进行4×4和5×5分块,则PmQm上波动场wm的法向导数∂νwm既可以表示成Ω(m)的每条边上波动场wm-1,u0,m,wm,u1,m的线性组合,也可以表示成Ω(m+1)的每条边上波动场wm,u0,m+1,wm+1,u1,m+2,u1,m+1的线性组合,再根据∂νwm的连续性能够得到除去PmQm以外的其余7条边的线性方程.对于超级晶格内其它公共边,可以用同样的方法构造线性方程.最终,所有公共边上的波动场w可以由u0,u1线性表出:

(8)

其中P0是m(N+N2)×m(N+N2)矩阵，P1是m(N+N2)×2(m(N+N2)+N1)矩阵。

另一方面,超级晶格边界上波动场的法向导数∂νu0,∂νu1有如下表达式:

(9)

其中Q0是2(m(N+N2)+N1)×2(m(N+N2)+N1)矩阵,Q1是2(m(N+N2)+N1)×m(N+N2)矩阵.将(8)式代入(9)式中可求得超级晶格的DtN映射M为:

(10)

且M是2(m(N+N2)+N1)×2(m(N+N2)+N1)矩阵.

对于图1所示结构,其表面模式是控制方程的一种形如下式的特解:

u(x,y)=e-iβxΨ(x,y)

(11)

其中β是实的传播常数,Ψ(x,y)是在x方向上以L为周期的周期函数,且当y→±时,u衰减到0.

将(7)式中的矩阵M进行2×2分块,再利用拟周期性边界条件u1=e-iβLu0,∂νu1=e-iβL∂νu0,最终得到线性特征值问题

(12)

通过求解得到特征值e-iβL，从而得到计算结构的单向表面模式.

4 数值算例

以存在着单向表面模式的两种不同的边界面结构为例来验证方法的有效性,第一种边界面位于旋磁光子晶体和各向同性光子晶体的交界处,第二种边界面位于两种不同的旋磁光子晶体的交界处.

(a) 色散曲线 (b) 点A1对应的电场分布图

图5(a)中的红色实线上的点A1(0.377 2,0.560 4)表示在归一化频率ωL/(2πc)=0.560 4时,存在传播常数βL/(2π)=0.377 2的单向表面模式.点A1的电场分布如图5(b)所示,从图5(b)中可以看出能量集中在两种光子晶体的交界处,在垂直于交界的方向上快速衰减到0.

图6 由两种不同的蜂巢状旋磁光子晶体组成的结构

第二个算例结构如图6所示,由Chen等人[6]提出.该结构由两种不同的蜂巢状旋磁光子晶体组成.蜂巢状旋磁光子晶体(晶格常数L=15 mm)均由旋磁各向异性材料制成的介质柱在空气中按蜂巢状周期排列组成,介质柱的折射率均为(15.26),右半部分介质柱的半径分别为a1=3 mm,a2=2.5 mm,左半部分介质柱的半径分别为a3=3.6 mm,a4=1.9 mm.当外加磁场H0=500 Oe时,μr=0.78μ0,μk=0.93μ0.取m=11,N=7[16-17],计算结果如图7(a)所示,其中单向表面模式存在于两种光子晶体的交界处,其频率范围为[0.261 5,0.322 6].计算结果同文献[6]中的结果一致.图7(b)给出了点B1(0.386 9,0.288 4)对应的单向表面模式的电场分布图.

这两个算例表明,利用DtN映射方法能够得到与有限元方法[5-6]完全一致的计算结果,但DtN映射方法的优点在于它只需要离散计算区域的边界,避免了对计算区域内部进行离散,从而极大地减少了未知数的个数,使得求解特征值问题时涉及的矩阵规模非常小,提高了计算速度.

(a) 色散曲线 (b) 点B1对应的电场分布图

5 结语

将DtN映射方法用于计算旋磁光子晶体单向表面模式.只需要离散超级晶格的边界,在边界上建立起一个以Bloch波矢的函数为特征值的线性特征值问题,该特征值问题涉及的矩阵规模小,求解速度快,且无论是对于色散介质还是非色散介质,该特征值问题都是线性的,因此DtN方法非常适合用于旋磁光子晶体的分析与计算.