因子服从指数分布的因子分析模型的参数估计研究

周国琼, 蒋文江

(1.昭通学院 数学与统计学院，云南 昭通 657000 ；2.云南师范大学 泛亚商学院，云南 昆明 650092)

在传统的因子分析模型中，因子被假设为服从标准正态分布，可取实数域上的任何值；而在日常生活中，往往存在一些非负或非正的数据，如学生成绩和寿命数据等，当对这类数据做因子分析时，假设因子服从一个非负的概率分布(如指数分布)是较为合理的选择.

传统的因子分析模型假设模型中各个公共因子及特殊因子之间相互独立且公共因子服从标准正态分布，因而可以直接利用极大似然估计[1-2]对模型中的参数做估计；但当因子分析模型的因子服从指数分布时，会导致模型中的似然函数没有显式表达，不能直接使用极大似然估计法估计参数[3]；针对这一情况，本文采用蒙特卡洛方法来解决极大似然估计中似然函数没有显式表达的问题，即利用基于EM算法的极大似然估计法对模型中的参数做估计[4-6]，其中EM算法中的E步采用马尔科夫链蒙特卡洛方法中的M-H算法[7]从一个非常规的复杂分布中通过抽样来完成积分计算[8].

1 模型及待估参数

设y=(y1,y2,…,yp)T是p维可观测的随机向量，μ=(μ1，μ2，…，μp)T是p维截距向量，Λ=(λij)p×q是p×q(p>q)维的因子载荷矩阵，x=(x1,x2,…,xq)T是q维潜在因子的随机向量，ε=(ε1，ε2，…，εp)T是p维误差随机向量，本文所研究的模型为

y=μ+Λx+ε

(1)

该模型与传统的因子分析模型[1]的不同之处是本文假设误差随机向量ε～N(0,∑)，其中∑=(σij)p×p为对角矩阵；潜在因子的随机向量x中每一个随机变量xk～exp(βk),k=1,2,…,q；误差随机向量的分量εj(j=1,2,…,p)与潜在因子随机向量的分量xk之间相互独立.模型中的待估参数有μ,Λ,Σ,βk,本文的核心工作就是对这些参数进行估计.

2 参数估计研究

2.1 模型参数极大似然估计的方法与原理

把模型(1)中的待估参数记为参数向量θ=(μ，Λ，∑，βk)，记Y=(y1,y2,…,yn)为观测到的数据矩阵，X=(x1,x2,…,xn)是潜在的因子矩阵.

2.1.1 模型的似然函数

由于潜在因子随机向量x的每一个分量之间相互独立且xk～exp(βk),所以随机向量x的联合密度函数

(2)

由于误差向量ε～N(0,∑)，所以当潜在的因子随机向量已知时，可观测随机向量y～N(μ+Λx,∑)，于是根据条件概率的定义可得y的条件概率密度函数[9]

(3)

根据式(2)和式(3)，基于观测数据Y的似然函数

(4)

对应的对数似然函数

(5)

(5)中的多重积分没有显式表达，所以很难通过极大化(5)来获得参数θ的极大似然估计[10].

为解决上述积分问题，考虑使用数据添加算法[11]，把潜在的因子矩阵X=(x1,x2,…,xn)看作缺失的数据添加到观测到的数据矩阵Y=(y1,y2,…,yn)中，从而得到完全数据矩阵Z=(X,Y)，然后用EM算法来获得参数θ的极大似然估计.

2.1.2 EM算法估计参数

记Z=(X,Y)为添加数据后的完全数据矩阵，由于把潜在的不可直接观测到的因子矩阵当作是已知的能够观测到的数据矩阵添加到观测数据Y中，式(4)和式(5)中对X的积分运算失效，则添加数据后的对数似然函数

(6)

通过EM算法可求得式(6)中参数θ的极大似然估计.

根据EM算法的原理[12]，基于θ的第t次迭代值对对数似然函数(6)中的X求期望，得到Q函数

(7)

需要计算的积分有E[xi|θ(t),Y]和E[xixiT|θ(t),Y].

利用蒙特卡洛方法，通过从密度函数p(x|y,θ)中抽取M个x的样本x(l),l=1,2,…,M，然后根据样本观测值对x求期望，得

由贝叶斯公式[13]可得密度函数

(8)

该密度函数并不是某一常见分布[14]的密度函数，所以想要用常规的方法从(8)中抽取x的样本非常困难[15].本文采用马尔科夫链蒙特卡洛(MCMC)方法中的Metropolis-Hastings(M-H)算法来对x进行抽样.

根据Metropolis-Hastings算法的原理[16]，视密度函数p(x|y,θ)为产生样本x的目标密度，然后找一个容易产生样本的分布作为建议分布，通常选取正态分布N(x(l-1),σ2Ω)作为建议分布[17]，其中x(l-1)是产生第l个x样本的上一步第l-1步所产生的x样本，Ω为目标密度关于x的Fisher信息矩阵，σ2是任一给定的调节参数，通过调整不同的σ2值来得到样本不同的接受概率，通常需要把样本的接受概率控制在0.25到0.50之间[18]，而目标分布与建议分布之间通过信息矩阵Ω进行联系.

根据极大似然估计原理，M步要对E步中所得的Q函数进行极大化，从而求得参数θ的极大似然估计，即解决优化问题

也即求解如下方程

用矩阵微商的求导公式[19]分别对函数Q(θ|θ(t))中的参数μ、Λ、∑和βk求一阶偏导,得

分别令上述一阶偏导为零，即可得每一个参数的估计式

2.2 EM算法的收敛准则

对于该模型参数的极大似然估计，本文在EM算法里采用的停止准则[20]是当估计值θ前后两次迭代值的绝对差值|θ(t)-θ(t-1)|<10-2时停止迭代，重复进行100次后计算参数极大似然估计的平均值；在EM算法的E步中，本文用M-H方法产生样本量为15 000的样本，然后使用后5 000个样本来进行统计推断，以保证所使用的样本来自目标分布.

2.3 模拟研究

基于所述的参数估计的方法及原理，下面对该模型中的参数估计问题进行模拟研究，从下述定义的因子服从指数分布的因子分析模型中产生模拟数据.

首先，假设模型中潜在因子随机向量中包含四个潜变量，即x=(x1,x2,x3,x4)T；可观测的随机向量中包含8个可观测变量，即y=(y1,y2,y3,y4,y5,y6,y7,y8)T，则模型为

y=μ+Λx+ε

待估参数有

上述矩阵中的常数表示不进行参数估计.根据模型的定义，共有31个待估参数，参数取如下真值进行模拟：

分别在样本量n为200、300和400的情况下进行100次重复估计并取其均值作为参数估计值(结果见表1).

从表1的模拟结果可知，每种样本量下参数估计值与真实值之间的偏差都较小，这表明用MCECM算法对该模型的参数做估计具有良好的效果，即估计值与真实值非常接近.特别地，当样本量为200时，真实值与估计值之间偏差绝对值的最大值约为0.06，而最小值约为0.001，所以在样本量为200的情况下，参数的估计结果较为准确；另一方面，随着样本量的增加，参数估计值的标准误差整体在逐渐减小，可见随着样本量的增加，参数的估计结果越来越准确，虽然其标准误减小的幅度较小，但可认为这种参数估计方法对样本量的要求不高，故MCECM算法对于参数估计而言具有较强的实用性，针对需要解决的参数估计问题，样本量的要求不是很高.

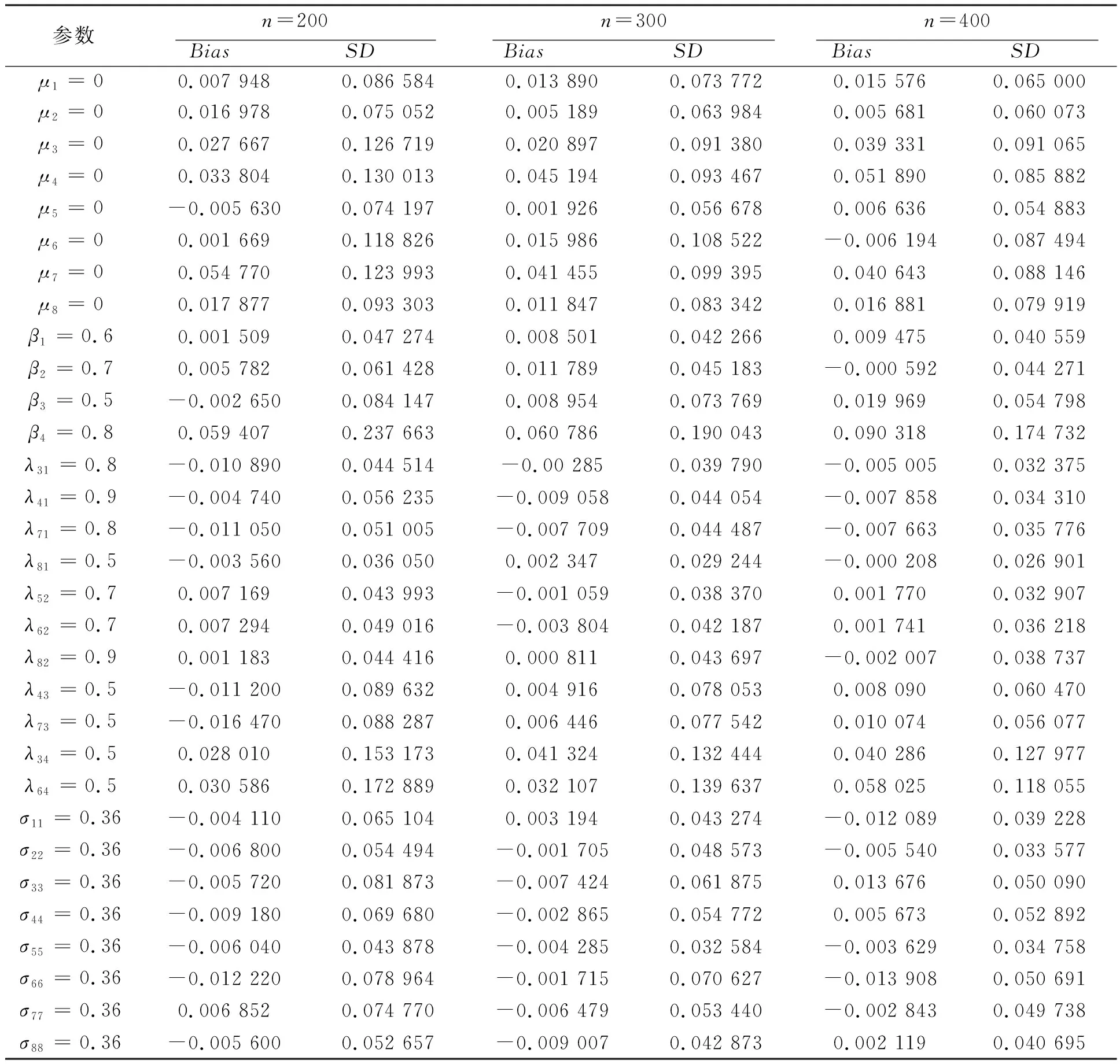
表1 参数模拟结果

n代表样本量；Bias代表真实值与估计值之间的偏差；SD代表标准差.

3 结语

针对诸多应用领域中相关数据为非负的情形，提出了一个传统因子模型的替代模型；用发展成熟的MCECM算法[21-22]来对模型中的参数进行估计.研究结果表明，用MCECM算法对因子分析模型中的参数进行估计是一种有效的方法.