基于GRECO与GO-PO算法的复杂目标RCS计算与分析*

（火箭军工程大学作战保障学院 西安 710025）

1 引言

随着现代高技术战争的不断发展，作战中如何提高己方武器装备的隐身能力，如何有效探测敌方武器作战平台日益成为攻守双方的关注重点，特别是随着采用新技术和新体制的高分辨雷达的不断涌现，对武器装备装备的隐身性能要求也越来越高。目标的雷达散射特性是雷达系统探测、跟踪、识别目标的基础，随着现代技术的发展和现代战争的需要，有效降低我方武器装备的雷达散射特性，及时准确获取敌方目标的雷达散射特性对赢得战争主动权，增强战斗力起着至关重要的作用。

对于电大尺寸复杂目标的雷达散射特性分析的高频近似法常用的有物理光学法（PO）、几何光学法（GO）、物理绕射理论（PTD）、几何绕射理论（GTD）、等效电流法（MEC），弹跳射线法（SBR）等，单纯用一种算法计算时显示出精度不高、计算耗时长的缺陷，近年来随着计算机技术的发展，采取多种射线追踪算法来提高计算效率的“混合算法”被广泛应用，不仅有效拓展了高频近似方法的应用范围，而且显著提高了计算精度。本文论述了基于GRECO与GO-PO算法的在电大尺寸复杂目标雷达散射特性分析上的应用，并与快速多极子算法（MLFMM）分析结果进行的对比分析，表明了此种方法的有效性。

2 雷达散射截面积定义

“雷达”原意为“无线电探测与测距”，当目标被雷达波照射之后产生的反射回波会带有隐含的目标的特征信息，雷达就是依靠接收这些反射回波，分析识别其中含有的特征信息来探测和识别目标。目标的回波之中隐含的，能够被雷达经过技术方法进行分类、辨识的特征信息，也称之为雷达目标特性。这其中最能反映目标隐身能力重要指标就是雷达散射截面积（Radar Cross Section，RCS），由电磁散射理论观点推导出来的雷达散射截面的定义式为[1]

式中：Ss、Es、Hs分别表示雷达接收机处的散射波的能流密度、散射电场、散射磁场；Si、Ei、Hi表示目标处入射波的能流密度、入射电磁、入射磁场。

雷达探测目标主要是靠接收目标反射的电磁回波来实现，其最大探测距离公式表述为

式中：R表示雷达的最大探测距离，G表示雷达的天线增益；λ表示雷达波长；σ表示目标的雷达散射截面积；Smin表示雷达的接收功率。

由公式可以看出，目标的雷达散射截面积σ的大小直接影响到雷达的探测距离和有效性，所以目标要减小雷达探测的作用距离和有效性，达到隐身的效果，主要途径是降低自身的反射回波能量和减小可能被雷达回波接收机接收到的反射回波，技术核心是降低目标的雷达散射截面积（RCS）。

3 计算方法

3.1 GO-PO分析方法描述

对于电大尺寸复杂目标的高频近似分析方法中，几何光学法（Geometrical Optics，GO）、物理光学法（Physical Optics，PO）较为常用。其中几何光学法（GO）是根据RCS的定义，假设目标的尺寸远远大于入射的雷达波的波长，电磁波在空间中的任意点的场在各个方向上具有同样的性质，将入射的电磁波等同于平面波入射，同时假设其满足电磁波局部性，能量的传播类似于电磁波在射线管中传播，各波束之间相互影响很小，将目标的雷达回波分解为目标上的众多的散射中心，通过费马原理确定散射中心，将这些散射中心所反射的散射场进行叠加而得到整个目标的散射场。

GO算法就是Luneberg-Kline级数展开的第一项，Luneberg-Kline级数展开式[1]：

式中，φr是相位因子，因此在GO即为一种近似的高频计算方法，将空间区域划分为了照明区和阴影区，GO的缺点就是没有考虑任何绕射产生的散射效应且对无曲率或单曲率表面计算时将得到无限大的RCS。

物理光学法（Physical Optics，PO）是通过计算目标表面电流所产生的感应场的大小积分而得到整个目标的散射场，主要是基于在曲率半径和照射波长远远大于入射波长，仅照明区域产生的表面电磁流且其特性没有发生变化的假设，此时目标所产生的感应场只取决于入射波，忽略了物体表面感应电流相互之间的影响和其他部分的散射能量。

由Maxwell方程组推导出目标表面的电磁流的可能选择，并满足一定边界条件下推导出Stratton-Chu方程[1]为

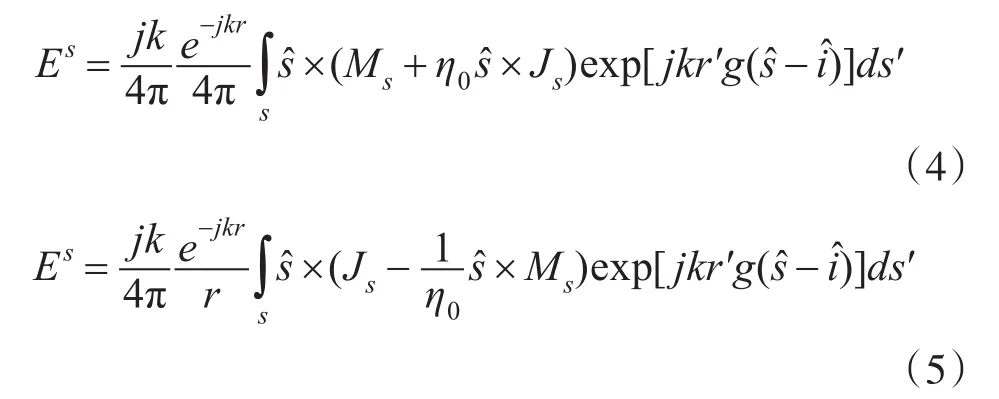
由式（4）、式（5）可以通过表面电磁流Js和M求解目标的散射场。式中表示入射和观察方向上的单位矢量，S表示目标表面的照明部分。对于理想导体，由于此时Ms为零，目标表面电磁流可表示为[1]

由此可以看出，物理光学法PO虽然克服了几何光学法GO在无曲率或单曲率表面得到无限大的RCS的缺点，但基础假设中，忽略了目标可能产生的表面感应电流之间的相互影响、以及多次反射产生的的散射能量，但像军事装备这类复杂目标体，各部分之间的多次反射所产生散射场对目标整体的RCS影响较大，如何忽略不计将产生较大的误差。

因此，几何光学与物理光学的混合算法（GO-PO）就是在应用物理光学法PO计算复杂目标组合体模型时引入几何光学法GO的计算方式，将经过多次反射的散射波在导体表面产生的感应电流产生的影响进行叠加计算，可以有效地提高计算准确度。其计算式为[2]

3.2 GRECO算法理论

随着计算机技术的发展，将计算机图形学理论应用到电磁散射计算中的图形电磁算法，日渐成为有效解决高频渐进算法的加速问题的有效途径。其中计算机图形学中应用最多是GRECO（图形电磁计算）算法，其中基本理论就是基于计算机图形显示与GO算法应用的面元Gardon的处理办法相似的原理，将三维场景在计算机屏幕上显示，根据屏幕光照强度的不同，对应出计算机GPU图形显示时的RGB值，由RGB值反向找到入射波的情况，提取参数。

计算机显示器显示图形是以像素为单位的，像素的多少对应着计算机的屏幕分辨率，如果能够将我们需要处理的目标的面元在计算机屏幕上进行完全的显示，那么屏幕上的每一个像素点也就对应了目标表面上的一个面元，至此，也即将目标表面按照像素进行了离散化处理。

运算过程中，通过应用OpenGL技术显示图形并追踪每个被照亮的面元，Phong式光照模型定义面元的法向量，Z缓冲区算法计算目标距离。OpenGL被认为是高性能图形和交互式视景处理的标准，具有非常快的渲染速度和筛选准确度。对于目标几何信息的获取，则通过Phong光照模型可知，适当选取光照模型以及物体的材质，如果使用的光源合适，计算机屏幕上每个像素的三原色强度分量仅由目标表面法矢与入射光的夹角有关。由此可以推导出，能够显示在屏幕上的便是可被电磁波照射到的面元，所以通过图形显示解决了物理光学法的入射波射线追踪的问题[5]。通过Z缓冲区算法进行消隐计算，判断遮挡，Z缓冲区主要是在计算机中存储每一可见像素的深度或Z坐标，Z缓冲区算法就是在给定数量的深度值中，不断的寻找最大的Z值，来排除隐藏面。计算中，引用Z缓冲区算法后，可以很好地解决目标的消隐问题，较大幅度地提高射线追踪的准确性和效率。

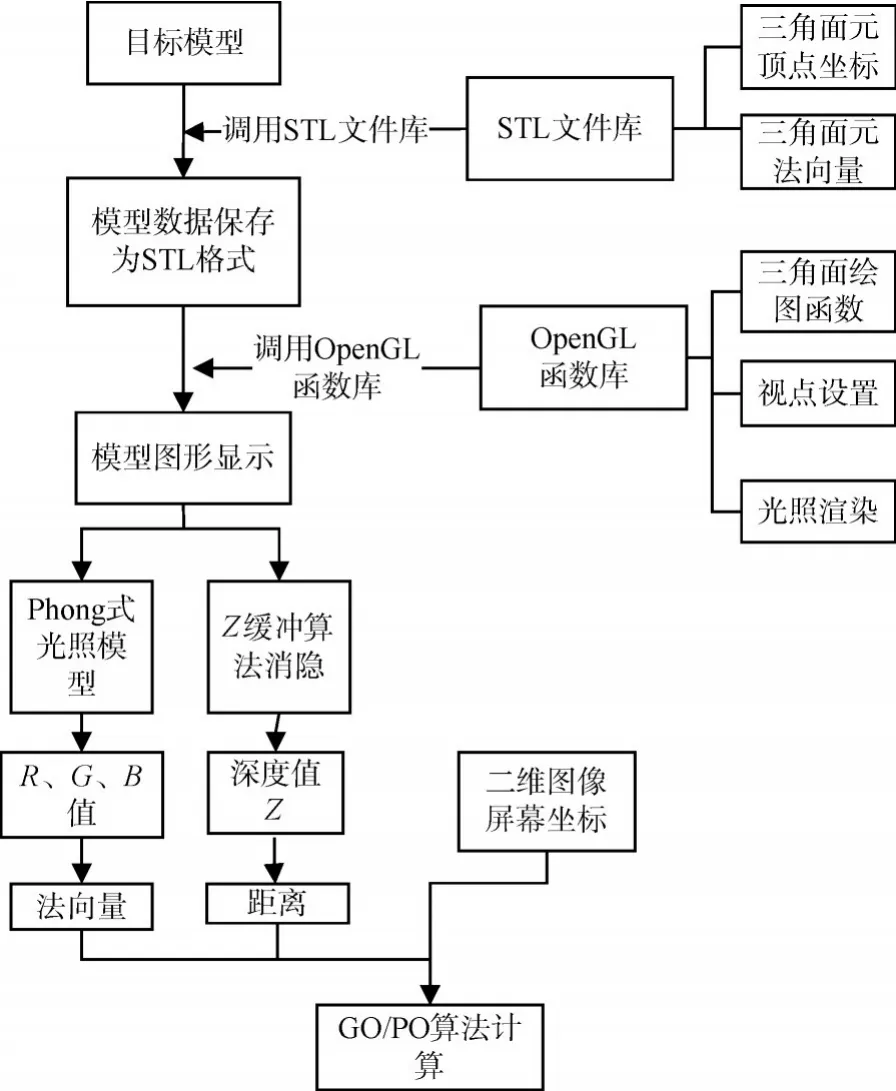
图1 加速算法流程图

如前所述，我们目标的几何模型建立完成后，按照GO-PO算法的部分要求，按照三角面元最大边长不超过模型最小尺寸的千分之一的要求[4]，对物体几何模型进行划分，转换成STL文件，利用OpenGL的三角面绘图函数读取目标STL信息中包括的三角面元顶点坐标和法向量，将几何形体成像于屏幕上，得到目标模型二维图像，并记录该二维图像的二维坐标。通过Phong式光照模型获得每一个三角面元特定的颜色，每个颜色值可以（R，G，B）三个值设置，通过OpenGL提供的glReadPixels函数读取其像素阵列信息，并以分析出被照射面元的编号，并获得其法向量，此时，加上计算机Z缓冲区中保存的Z值和二维图像的屏幕坐标，每个三角面元对应了一个六维矢量，由此即为物理光学法计算提供了完备的目标几何数据。再通过GO-PO算法计算位于照明区的三角面元的对散射截面的贡献值。加速算法整个计算过程如图1所示。

4 实例分析

4.1 角反射器RCS计算分析

为验证上述算法的有效性，先构建一个具有多种散射机理的二面角结构的金属反射器。如图2所示，二面角结构由两块边长为179mm的正方形金属板构成，平板厚为2.66mm，入射波与Z轴夹角代表入射角，用θ表示，入射波与X轴夹角代表方位角，用φ表示，当入射波沿X轴入射时，φ＝0°，θ=-90°；两种物体材料属性均设置为导体，仿真计算时入射波在XOZ平面内，频率为9.4GHz，垂直极化。图3为二面角结构的金属反射器RCS随入射角θ的变化图，此时θ的变化范围为-80°～80°，方位角φ=90°。

图2 二面角结构的金属反射器

图3 二面角RCS随入射角θ变化图

为了验证仿真结果的有效性，图3将通过基于GRECO与GO-PO算法的二面角RCS计算结果与文献[1]中采用时域有限差分（FDTD）算法的计算结果进行对比。时域有限差分法（FDTD）是一种典型的时域全波分析方法，是以Maxwell方程组作为出发点，在每一网格反复运行有限差分迭代式来求解电磁问题，因此FDTD算法是发展迅速，应用范围最广的数值方法之一[1]。通过图3可以看出，应用GRECO与GO-PO算法计算的二面角金属反射器RCS与文献[1]采用时域有限差分（FDTD）算法计算结果基本一致。

4.2 组合体RCS计算分析

为了进一步验证GO-PO算法在复杂目标散射计算上的准确性，先构建一个由长方体和圆柱体构成具有多种角结构的反射体，在一个平板上构建起一个长方体和一个圆柱体的结构，组合体各结构具体尺寸、坐标参数设置如图4所示，坐标参数、入射波参数设置同上例，φ表示方位角，θ表示入射角，入射波在XOZ平面内，当入射波沿X轴入射时，φ＝0°，θ=-90°；入射波频率为30GHz，垂直极化。图5为长方体和圆柱体组合模型RCS随方位角φ的变化图，此时φ的变化范围为0°～360°，θ=90°；图6为组合模型RCS随方位角φ变化的极坐标图；图7长方体和圆柱体组合模型RCS随入射角θ的变化图。

图4 长方体和圆柱体组合模型

图5 组合模型RCS随方位角变化图

对比图5、图6长方体、圆柱体组合模型RCS随方位角φ的变化图可以看出，在入射角θ=90°保持不变的情况下，在不同方位角用GO-PO算法与PO算法的结果十分相似，仅在120°、170°200°等部分方位角，GO-PO算法比PO算法的RCS值大。从图7组合模型RCS随入射角θ变化图，可以看出，随着入射角θ由－90°～90°的不断变化，组合模型中长方体、圆柱体与平板之间构成的角反射结构，多数位于GO-PO算法的光照区，引起的多次散射效果明显，而单纯应用PO算法计算的结果，由于忽略了多次散射对RCS的影响，RCS值较小，与GO-PO算法计算的结果具有较大的误差，可以看出，复杂的电大尺寸目标因为结构复杂，构成的角结构增多，能否有效地计算出多次散射产生的散射强度，对于目标的RCS值将产生较大影响[7]。通过对组合体RCS计算，进一步证明了基于GRECO的GO-PO算法在计算复杂目标的RCS的有效性。

图6 组合模型RCS随方位角变化图

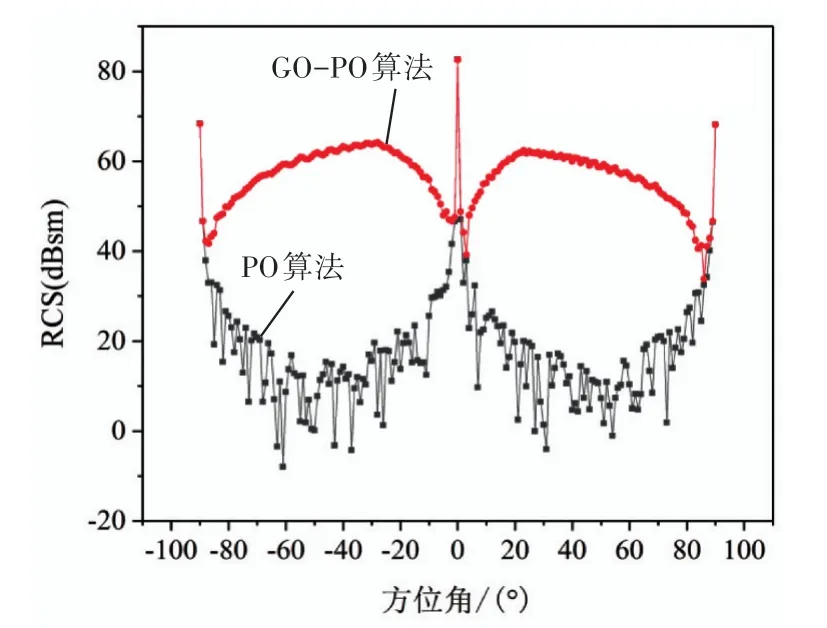
图7 组合模型RCS随入射角变化图

5 结语

对于复杂目标的RCS计算，非镜面散射和各部分之间的多次反射对目标整体的RCS影响较大，将几何光学法GO的运算机理融入物理光学法形成的混合算法（GO-PO），综合考虑多路径散射对RCS的影响，可以有效地保证计算精度，同时应用GRECO理论，可以快速地判断出位于照明区的面元，从而有效提高计算速度。通过对二面角金属反射器和长方位、圆柱体构建的组合模型进行计算，并将计算结果分别与时域有限差分（FDTD）和物理光学法PO计算结果进行对比分析，证明GO－PO算法在计算复杂目标的RCS中的有效性。