基于模糊Petri网的导弹装备可靠性评估研究*

（火箭军工程大学 西安 710025）

1 引言

导弹装备具有系统庞大、组成单元众多、部件结构复杂等特点，且各个组成部分、单元之间相互联系，彼此影响，其可靠性分析及评估必须综合考虑各层次系统的可靠性状态及其之间的相互影响。可靠性是衡量装备是否完成规定功能的标准，但目前进行可靠性评估主要采用故障树分析模型、故障诊断分析模型、贝叶斯网络模型等[1]，综合来看，这些模型对系统参数、子系统评估得多，对系统整体研究得少，虽然它们也较好地对导弹装备可靠性进行了评估，但在评估工作中没有完全考虑整体效果，以致于不能真实反映导弹系统可靠性的动态演化过程。

导弹装备可靠性变化是一个经典的动态变化，Petri网建模方法可以很好地描述其发展过程，由于可靠性在导弹装备系统中，由于导弹系统相互作用、相互依存，普通Petri网建模方法很难满足其可靠性评估的要求。黄睿、刘小方等利用Petri网建立了复杂系统性能质量评估模型[2]，基于此基础，笔者引入模糊理论，并针对导弹装备系统组成及可靠性变化规律，建立基于模糊Petri网的导弹装备可靠性评估模型，并结合某型导弹装备进行了实例验证。

2 模糊Petri网

2.1 Petri网（PN）理论

Petri网最早由 C.A.Petri博士首次提出[3]，是一个图形化的数学建模工具。通常情况下，我们可以用小矩形或者短黑线来表示一个变迁，用小圆圈表示库所，从而构成Petri网[4]。经典的Petri网是简单的过程模型，一个经典的Petri网由四元组（库所，变迁，输入函数，输出函数）组成，如图1所示。

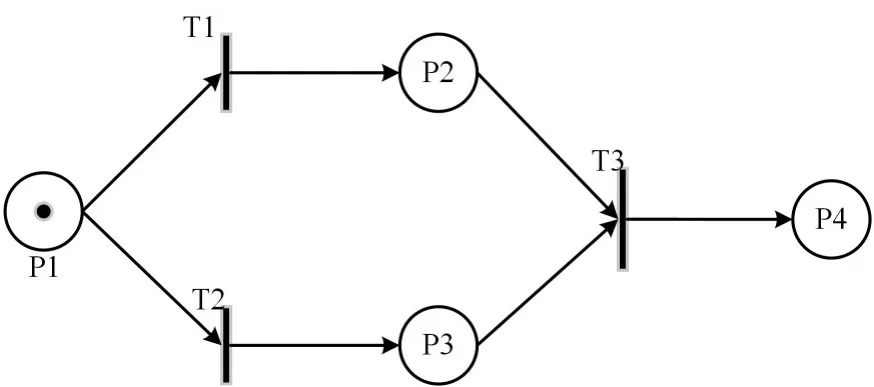
图1 经典的Petri网

2.2 模糊Petri网

模糊Petri网（Fuzzy Petri Net，FPN）是Petri网将模糊理论和Petri网理论相结合，通过奢侈品扩展。通过Petri网的图形化描述能力，知识的表达简单明了。知识规则库体现了规则间的结构特征。根据导弹装备系统的特点和可靠性变化规律，讨论了Petri网理论和导弹装备系统的可靠性评估模型如下：

FPN 定义为一个九元组[5]：FPN=（P，T，D，I，O，μ，α，β，λ）。

其中：

P为一个库所的有限集合，P={p1，p2，…，pm}；

T为所有变迁的有限集合，变迁和输出库所数量一一对应，T={t1，t2，…，tn}；

D为一个有限的命题集合，D={d1，d2，…dm}；

P∩T∩D=Φ，P∪T≠Φ，|P|=|D|；

I:P→T为库所到变迁的映射，表示为输入函数；

O:T→P为变迁到库所的映射，表示为输出函数；

μ：T→[0，1]为其变迁到其置信度的映射关系，即变迁规则可信度，μ(tj)(j=1，2，…，n)是tj的可信度，μ(tj)=u；

α：P→[0，1]为库所到其托肯值的映射关系，即库所的隶属函数，α(pi)(i=1，2，…，m)表示pi的隶属度；

β：P→D为库所P到其命题的映射关系，即di=β(Pi)；

λ：T→[0，1]为变迁T到其阈值的映射关系，为变迁的出发阈值集，当α(Pi)≥λ时，变迁ti才会被触发。

2.3 模糊产生式规则

假设R为模糊产生式规则集R={R1，R2，…，Rn}，那么第i条模糊产生式规则[6～9]为

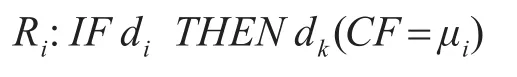
其中，dj和dk为包含一些模糊变量的命题。其取值范围在0～1之间，dj代表命题的真值。通常，在导弹装备可靠性评估中，dj代表的是每条模糊产生式规则的低层单元可靠性，dk代表的是高层单元可靠性。μi为置信度（CF），代表每条规则的可信程度，μi越大，则第i条规则越可信。

其简单形式如图2所示。

图2 模糊Petri网可靠性分析规则模型图

第①类规则的Petri点燃之后，运算可得：α(pk)=α(pi)*μ(t)；第②类规则的Petri网点燃以后，运算可得：α(pk)=MIN(α(p1)，α(p2)，…，α(pn))*μ(t)；第③类规则的Petri网点燃之后运算可得：α(pk)=MAX(α(p1)*μ(t1)，α(p2)*μ(t2)，…，α(pn)*μ(tn))。

3 基于FPN的导弹装备可靠性评估模型

3.1 影响因素分析

导弹装备各分系统可靠性的高低程度影响导弹整弹发射和任务完成情况，从而影响导弹整体可靠性。

图3 导弹各系统可靠性影响程度

图3所示图中的水平坐标系是指某一导弹的组成系统，按其对导弹的重要程度自上而下排列，即弹头、发射系统、控制系统、遥感系统；其次，从导弹弹头的角度看，主要因素是弹头。发射是影响导弹发射成功率的两个主要因素，它对导弹整体可靠性影响最大。

3.2 模型构建

某型导弹装备是某部队现役装备，由3级系统（A、B、C）组成如图4所示，现对其在役阶段可靠性进行评估。

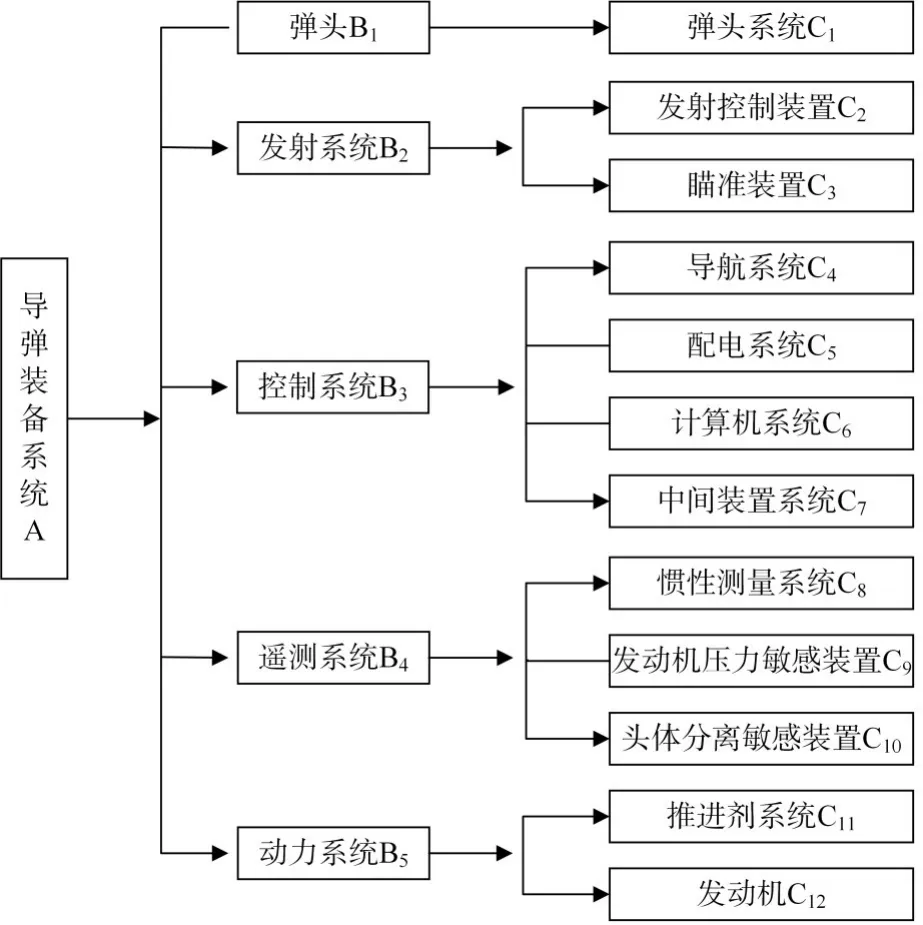
图4 某型导弹装备三级系统结构图

根据FPN理论和导弹装备系统特点及可靠性变化规律，结合某型导弹装备各子系统之间相互影响关系，建立的基于模糊Petri网的某型导弹装备可靠性评估模型如图5所示。

图5 某型导弹装备可靠性FPN模型图

4 实例验证

基于FPN的导弹装备可靠性评估模型主要根据输入部件及单元的可靠性，评估输出部件及单元的可靠性。根据FPN层次性的特点建模，可以将导弹装备可靠性评估过程中的层次化的实际情况较好地描述出来。在对导弹装备进行可靠性评估时，可以将系统整体分解为多个子系统，运用FPN模型，先评估子系统的可靠性，再由子系统评估系统整体的可靠性，从而实现系统整体可靠性的有效评估。各系统可靠性水平可以用四级等级的形式表示，如表1所示。

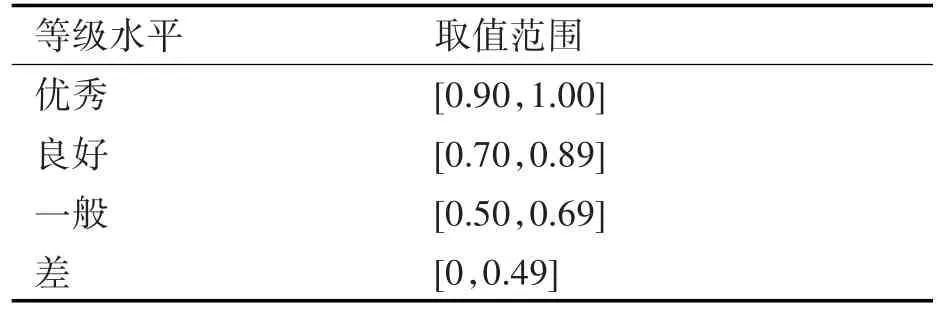
表1 可靠性等级取值范围

某型导弹装备各分系统可靠性评估成绩（初始库所）可根据相应分系统可靠度和点估计计算得到，具体过程不再赘述，评估成绩见表2。

表2 各输入库所的可靠性评估成绩

各库所之间的影响置信度如表3所示。

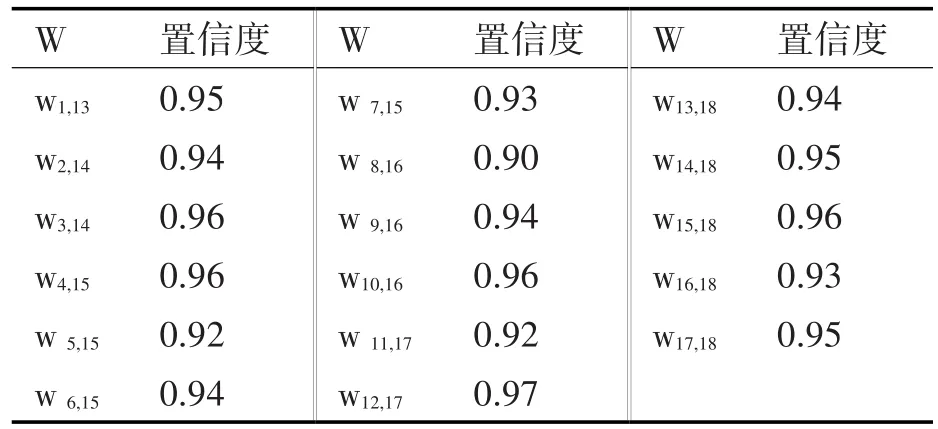
表3 各库所之间的影响置信度

根据各输入库所的系统的可靠性水平和库所之间的置信度，可以评估其他分系统可靠性以及系统整体的可靠性，评估成绩如表4所示。

表4 导弹分系统及系统整体可靠性评估成绩

根据评估成绩，该型导弹装备可靠性为0.8846，属于良好级别，可以较好完成任务。分析表2和表4可以发现，通过FPN模型，既评估得到了系统整体的可靠性水平，也得到了各分系统的可靠性。

5 结语

通过借助Petri网对系统因果关系的描述与分析能力，用Petri网对导弹装备系统进行了层次分析，并针对导弹装备特点，结合模糊逻辑建立了模糊Petri网模型，实现了对系统变化的推理过程，提高了导弹装备可靠性评估的针对性、适应性和精确度。实例表明，该模型能够很好地对导弹装备可靠性进行分析评估。