基于概略角内声呐浮标阵效能评估*

（海军航空大学 烟台 264001）

1 引言

随着潜艇规避战术的发展，新型材料不断应用在潜艇上，使得现代反潜过程中搜到潜艇的概率越来越低。声纳浮标是反潜巡逻机的主要装备，具有携带，布放方便，快速形成大面积搜索阵等优点[1]。如何既能节省浮标，又能更快地搜索到敌目标，是反潜巡逻机在搜潜时考虑的重要环节。实际作战中，一般根据任务要求，作战方法，搜索区域的大小和形状，采取不同的浮标包围阵[2]。有时，在实际作战中，我们可以通过某一些区域确定潜艇的概略航向角，根据潜艇的初始概略位置和概略航向角，通常将声呐浮标布放成圆形阵，直线阵和斜线阵[3]，本文将通过计算在不同概略角情况下，使用蒙特卡洛方法，计算出每种类型的浮标阵的搜潜概率，需要的浮标个数，得出在作战中最优的浮标阵型，为巡逻机在反潜作战中的浮标阵型选择和投放提供数据支撑和理论依据。

2 潜艇的位置散布

当反潜巡逻机到达反潜区域后，潜艇的位置存在着以初始点为圆心半径为R的圆散布，其中半径R的大小与反潜巡逻机准备起飞时间，飞行时间和潜艇航速有关，对于潜艇的航速，大体有两种假设，一是潜艇未知被发现，则按照经济航速航行，二是潜艇已知被发现，潜艇将按照最大速度进行规避[4]。

在以往的声呐浮标效能的评估中，对潜艇的位置散布只做简单的假设，搜潜概率也是简单的用浮标阵的覆盖面积与潜艇散布的面积之比，不能准确地对浮标阵型进行效能评估，所以为了尽可能对搜索手段的效能进行准确的评估，本文将建立潜艇位置散布规律，基于散布规律求出不同搜索手段的搜潜概率，对声呐浮标效能进行准确的评估[5]。在应召反潜中存在航速航向已知，航速航向未知，航速已知航向未知，航向已知航速未知等背景下的潜艇散布规律，由于本文讨论的便是概略角内的声呐浮标阵的效能评估，所以只建立了航速未知，航向已知的潜艇散布规律模型。

当潜艇的航速未知时，一般认为潜艇以经济航速航行，假设潜艇的速度服从方差为δv的瑞利分布[6]，则速度概率分布的表达式为

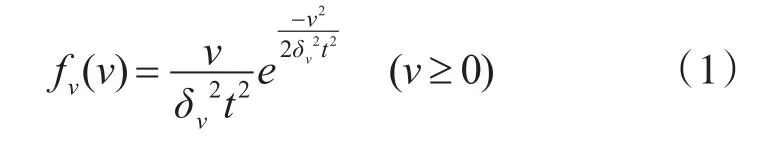
式中t表示为t时刻后潜艇的散布。

航速v的期望为

潜艇的经济航速为vs，假设潜艇的经济航速就是速度的期望值，则方差δv的表达式为

又因为δr1=δvt，可以得到：

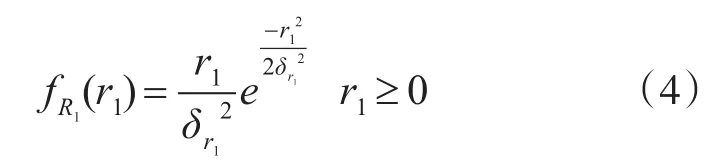
所以在极坐标下表达式为

其中φa是概略角的一半，也称为航向误差，α是潜艇的航向角，δ02是目标初始位置的散布，通常0.5≤δ02≤8(km)。

潜艇散布规律的完整表达式为

假设δ02=2，潜艇的平均速度为8kn，14.816km/h ，航向概略角为 90°，所以φa=45°，潜艇运动时间为t=1h，通过上述条件，得到了概略角已知，航速服从瑞利分布的潜艇概率分布图。

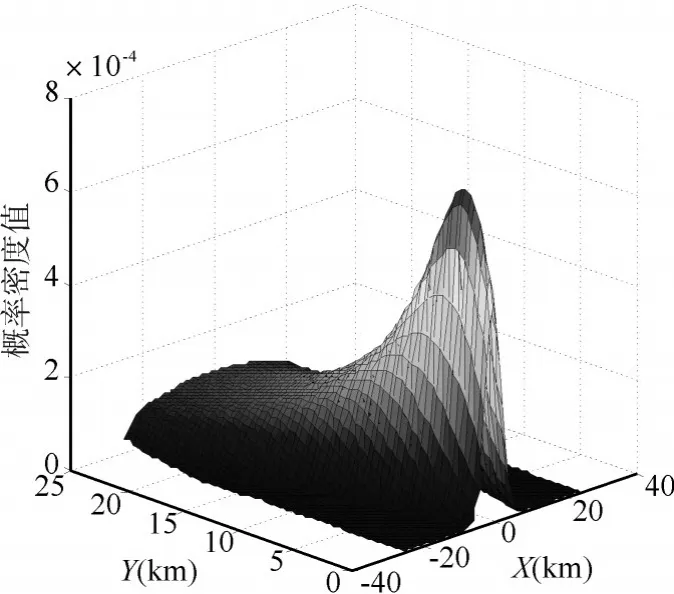
图1 航向已知航速未知的潜艇概率分布图

为了更加直观地表达出不同点的概率密度值，本节将三维图转化为了二维等高线图，如图2所示。

图2 航向已知航速未知时概率密度分布图

潜艇的概率分布图能更好地把潜艇在一段时间后的散布表现出来，基于潜艇概率分布求出来的搜潜概率是最准确的，对声呐浮标阵效能的评估也是最有说服力的。

3 浮标探测距离模型分析

反潜巡逻机在布放浮标阵前，对浮标声呐作用距离的预测是非常重要的，第一，根据被动浮标的探测距离确定浮标之间的间距系数k，Det为浮标的探测距离，通过间距系数可以求出浮标间距D为[7]

浮标之间的距离可以预测所布放的阵型需要的浮标个数和布放点的位置。第二，根据浮标实际探测距离可以解出浮标阵是否探测到潜艇，假设t时刻潜艇的位置为(xsub0，ysub0)，浮标的位置坐标为(xdipi，ydipi)，浮标的个数为N，i∈[1，N]。当

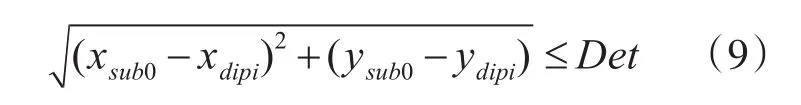
通过上述表达式来确定浮标阵是否探测到潜艇[8]。

声呐浮标的主要工作于被动方式，所以声呐浮标工作时的声呐方程为

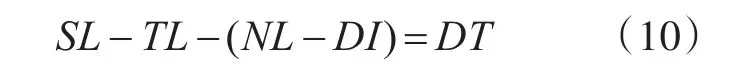
其中SL是潜艇的辐射噪声级，TL为传播损失，NL为海洋环境噪声，DI为接收机指向性指数，DT为检测阈值。

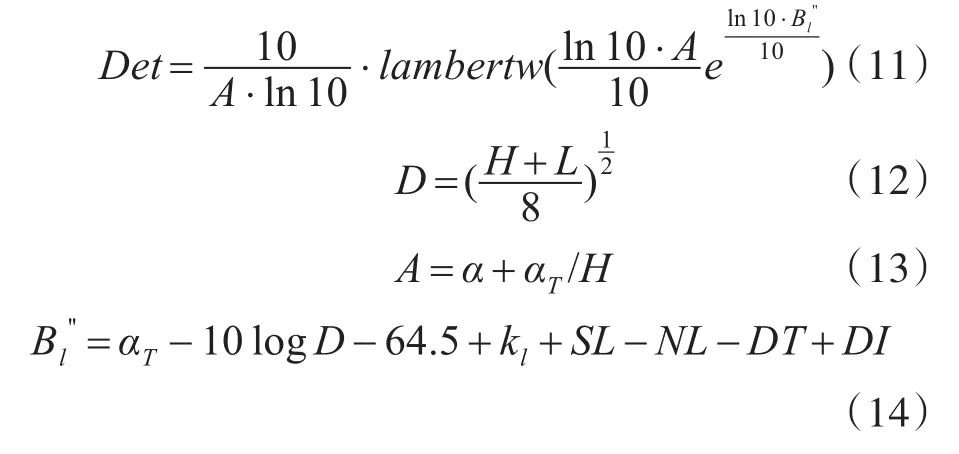
α为海水吸收系数，αT为浅海有效衰减系数，kl为近场异常衰减，H为水深，L为混合层深度。图3给出了浮标探测距离随潜艇航速与αT的关系。

图3 浮标探测距离随潜艇航速与αT的关系

从图中可以看出浮标的探测距离随着潜艇航速和浅海有效衰减系数变化而变化[9]，浮标作用距离的大小0≤Det≤6(km)，通过本节的计算，为后续浮标阵效能评估提供数据上的支持。

4 概略角内的典型阵型

概略角内的典型阵型主要包括弧形阵，直线阵和斜线阵三种典型阵型[10]。

4.1 弧形阵

对于弧形阵覆盖的面积应该尽可能覆盖潜艇可能的散布区域，确保浮标阵能够最大可能性地拦截到潜艇目标，第一个弧形半径为R0，第二个弧形半径为R1，则有：vse是平均速度，vs是最大速度，tdelay为接受任务到第一个浮标投放点的时间。

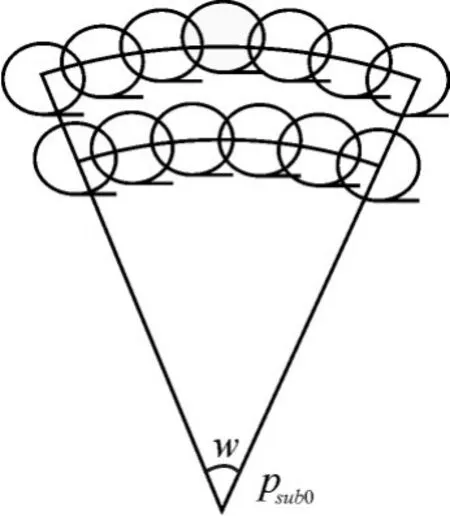
图4 弧形阵搜索示意图

潜艇初始概略位置于反潜巡逻机的距离为

所以延迟时间为[11]

列车运营日计划编配问题可表述为：在时刻表/车次信息、股道信息、车组信息已知情况下，对列车运营日计划表进行编配。列车运营日计划要满足道岔转换最小时间约束、早高峰指定车次约束、出库便捷性约束和唯一性约束，选用合适的良好车组去担当特定的列车车次。

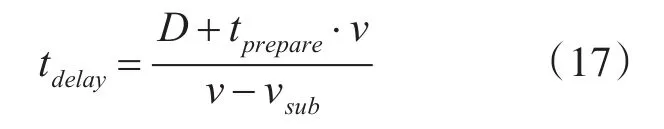
tprepare为飞机准备飞行时间，vsub为潜艇的航速，v为飞机的巡航速度。

弧线上相邻浮标点的关系如图5所示。

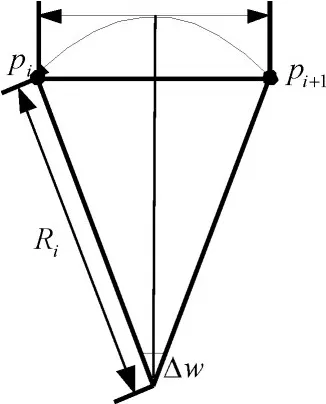
图5 弧线上相邻浮标点的关系

由上式可以得到两个浮标中间的夹角：

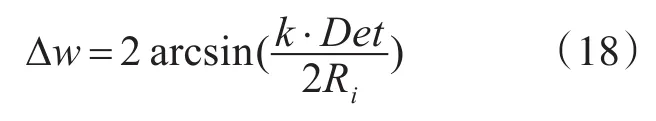
所以每条弧线上的浮标个数为N，表达式为[12]

其中w为潜艇航行的概略角，fix是把数值向下取整。则两个浮标间的实际夹角为

则第i条弧线上第个j探测点的坐标为

4.2 直线阵

图6 弧形阵搜索示意图

直线阵上一条拦截阵的简图，如图7所示。

其中Li=vsub·tdelay，vsub是潜艇的航速。

由三角函数的关系，可以得到拦截阵的长度为

假设一条拦截阵需要浮标的个数为N，则：

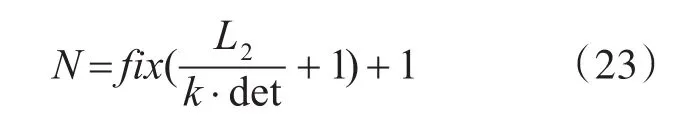
那么真实的k值为

则第i条直线上第个j探测点的坐标为

4.3 斜线阵

图8 斜线阵搜索示意图

斜线阵上一条拦截阵的简图，如图9所示。

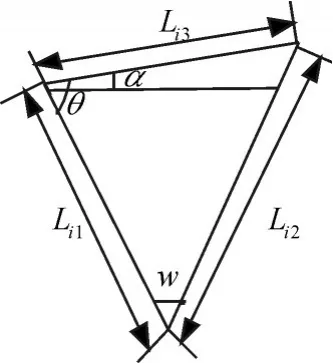
图9 斜线阵上一条拦截阵的简图

根据简图可以得出Li1=vsub·tdelay，Li2=vsub·(tdelay+tb)，Li3=vb·tb，其中vb是巡逻机布放浮标时的速度，tb为布放时间。

根据余弦定理可以列出下列表达式：

通过上述表达式可以求出布放时间tb，根据布放时间可以求出三角的每条边长，根据正弦定理得：

从上述表达式中可以得到斜线阵的斜率为

布放斜线阵需要浮标个数为N，则：

则第i条斜线上第个j探测点的坐标为

5 仿真分析

5.1 仿真条件

反潜巡逻机的位置为(0，0)，潜艇的初始位置为 (400，400)(km)，反潜巡逻机的巡航速度为v=550km/s，布放时的速度为vb=350km/s，潜艇初始的散布为δ02=2，潜艇的经济航速为vse=5kn/h，最大航速ve=2vse，飞机起飞前的准备时间为tprepare=10min，浮标的作用距离Det=3km，间距系数k=1.8，巡逻机监视时间为t=1.5h，本文考虑在概略角w=90°中，使用蒙特卡洛的方法对每个阵型仿真5000次，得出每个阵型的搜潜概率。

5.2 仿真结果

在概略角w=90°中，潜艇初始位置服从正态分布，航向服从均匀分布，速度服从瑞利分布。

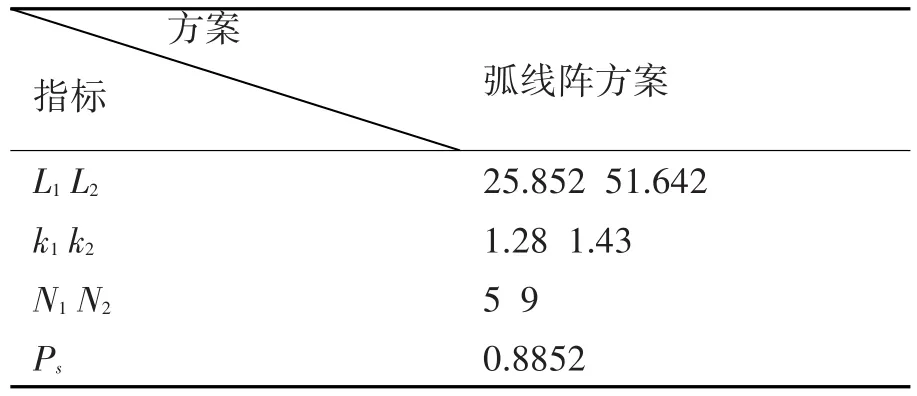
表1 弧形阵下各种指标

表1是在概略角w=90°时的仿真结果，其中k1、k2分别是两条弧线的间隔系数，N1、N2分别是两条弧线需要的浮标个数，L1、L2分别是两段弧线的长度，ps是搜潜概率。

在概略角为w=90°时对直线阵进行仿真，得到各指标结果如表2。

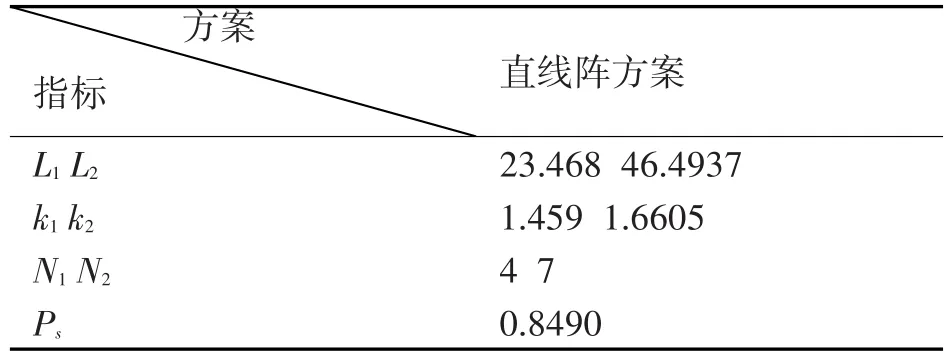
表2 直线阵下各种指标

在概略角为w=90°时对斜线阵进行仿真，得到各指标结果如表3。

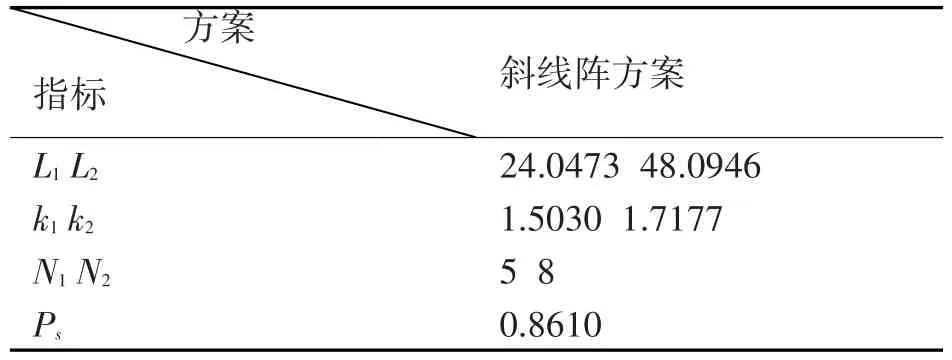
表3 斜线阵下各种指标

从表中可以看出，圆形阵的搜潜效率最好，斜线阵次之，直线阵最少，并且不同的浮标阵所需的浮标个数不同。

概略角不同需要的浮标的个数也不相同，如下图所示在概略角w∈(50°，120°)内，浮标的个数随概略角变化的曲线。

图10 浮标个数随概略角变化曲线

随着概略角的变化，浮标阵需要的浮标个数不同，搜潜概率也会发生相应的变化，图11所示在概略角w∈(50°，120°)内，搜潜概率在不同阵型下随概略角变化曲线。

通过图中曲线可以看出，在概略角w≤80°时，直线阵和斜线阵的搜潜概率比较大，在浮标比较充裕的情况下可以选择斜线阵，如果浮标数量有限，则选择直线阵。当概略w≥80°时，选择弧形阵，搜潜效果会更好。

6 结语

为了提高在概略角内的反潜效能，采用布放浮标阵的的方法，建立了三种反潜巡逻机布放声呐浮标阵搜潜模型，通过在一定的概略角内对三种浮标阵进行仿真，得出了每个浮标阵的性能指标。通过改变概略角的大小，得出不同情况下需要浮标的数量。最后比较了不同概略角下三种搜潜模型的搜潜概率，得出了当概略角w≤80°时，直线阵和斜线阵优于弧形阵，当概略角w≥80°时，弧线阵优于其他阵型。该研究对于提高反潜巡逻机反潜作战能力有一定的理论意义。