基于模糊电子凸轮曲线控制的经编机电子横移控制系统
2020-12-02沈瑞超郗欣甫蔡飞飞孙以泽
沈瑞超, 郗欣甫, 蔡飞飞, 孙以泽
(东华大学 机械工程学院, 上海 201620)
经编面料被广泛应用于泳衣、内衣、运动鞋服、汽车内饰等产品上。随着生活水平的提高,人们越来越多追求产品的个性化,这就要求经编机具有适应多品种、小批量、大花高的能力,显然采用花盘凸轮的传统经编机不具备这些能力。而采用电子横移的经编机可根据花型计算各梳栉的横移量,从而伺服电机通过滚珠丝杆控制各梳栉横移,因此,采用电子横移的经编机可根据市场需求生产不同的经编面料。但是经编机中梳栉运动的复杂性和高动态响应性,以及受限于伺服电机的性能,使得采用电子横移的经编机很难做到高速运行。
近年来很多研究人员对经编机的电子横移控制方案进行了研究。例如,付睿云等[1]和苏柳元等[2]采用改进型双T网络陷波滤波器,消除了横移传动系统的机械谐振点,提高了系统伺服刚度,进而提高了横移系统的稳定性和跟踪精度。Li等[3]设计了一种基于数字信号处理器(digital signal processor,DSP)的经编机电子横移控制系统,采用直线电机驱动电子横移动作。张琦等[4]提出一种动态变结构的经编机电子横移控制策略,提高了横移伺服的定位精度和动态响应。这些方法虽然都可以在一定程度上提高横移伺服的动态响应,但只考虑到电子横移本身的控制策略,而未结合经编机的工艺特点进行研究。
凸轮系统的一个独特特点是主、从动件关系总是重复的,即主动件和从动件的位置是同步的,并且对于凸轮轮廓上的相对给定点彼此锁定。这种关系对于执行重复操作的机器而言是非常有用的[5]。电子凸轮既有机械凸轮机构分度运动的特点又有输出运动可控的特点,在现实生产中可通过改变控制算法实现不同运动规律的自由切换[6]。
本文通过对经编机电子横移的运动特性以及不同凸轮曲线的特性进行分析,设计了一种基于模糊电子凸轮曲线控制的经编机电子横移控制系统。该控制系统可以根据不同的工艺和主轴转速,动态修改电子横移的电子凸轮曲线类型,从而避免由于电子凸轮曲线影响经编机主轴转速的提高,同时在横移伺服性能允许的前提下选择性能最优的电子凸轮曲线。
1 基于电子凸轮的电子横移控制系统
1.1 控制系统整体结构
基于电子凸轮的经编机电子横移控制系统原理图如图1所示。用户可通过触摸屏选择花型、主轴转速、横移角度等。PLC(programmable logic controller)根据所选的主轴转速控制主轴运转,主轴编码器返回主轴实时角度等信息。PLC根据返回的主轴角度及用户选择的横移角度和花型参数,计算各横移轴相对主轴的凸轮曲线,依据该曲线控制各横移轴移动,从而完成特定花型的编织。
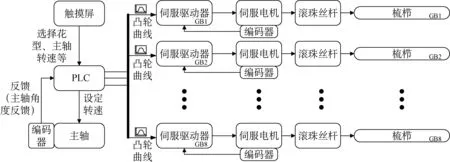
图1 高速经编机电子横移控制系统原理图Fig.1 Principle diagram of electronic shogging control system for high speed warp knitting machine
1.2 经编机电子横移轴运动特性分析
目前采用电子横移的经编机的最高机速往往可达1 000 r/min以上。以某公司研制的RD7-EL-138-E22双针床经编机为例,主轴每旋转一圈,导纱针要完成前针背、前针前、后针背以及后针前的各一次垫纱。由于导纱针在经过织针平面时梳栉不能横移,这就要求伺服运动具有“运动-停止-运动-停止-运动-停止-运动-停止”8个步骤,即主轴旋转一圈,横移伺服电机需要完成4轮加减速,并且每次移动前后要留足够的时间,用以导纱针经过织针平面。因此,实际留给横移伺服移动的时间非常短。在如此短时间内要想完成工艺要求的横移距离,就要求横移伺服具有极高的加、减速度和动态响应性,并且横移伺服电机需频繁启动和停止。根据经编机横移轴的运动特性,选择松下MSMF082L1U2M型伺服电机作为横移伺服电机。表1为所选伺服电机的参数。

表1 伺服电机参数
伺服电机的最大理论加速度按式(1)计算。
(1)
式中:amax为伺服电机最大加速度;Fmax为伺服电机最大力矩;fmax为机器摩擦力矩;J为伺服电机转子转动惯量;c为转子惯量与负载惯量比。
实际测得梳栉移动的摩擦力矩为1.67 N·m,转子惯量与负载惯量比值为1.1,根据式(1)计算得到amax=2.723×104rad/s2。因此在伺服运行中最大加速度不能超过该理论值。
横移伺服电机的加速度突变将产生较大的惯性力,从而产生柔性冲击,这将影响设备的寿命和定位精度。但若是采用恒定加减速度运行,则会在启动和停止时产生柔性冲击。因此高速运转时横移伺服不能采用恒定加速度运行,这就需要对电子凸轮曲线进行设计,以减轻运行时产生的柔性冲击,同时最大限度发挥横移伺服的性能。
1.3 电子凸轮曲线选择
由于凸轮曲线的特性直接影响从动件的动态性能、效率和寿命,因此,凸轮曲线的设计对于经编机电机横移的性能至关重要。正弦系列和多项式系列曲线都是性能较为优良的曲线,被广泛应用于各种中、高速自动机械[7],因此,这些曲线非常适合用于经编机电子横移的运动曲线规划。利用Matlab软件对修正正弦曲线、5次多项式曲线和7次多项式曲线的速度、加速度以及加加速度进行分析,结果如图2所示。
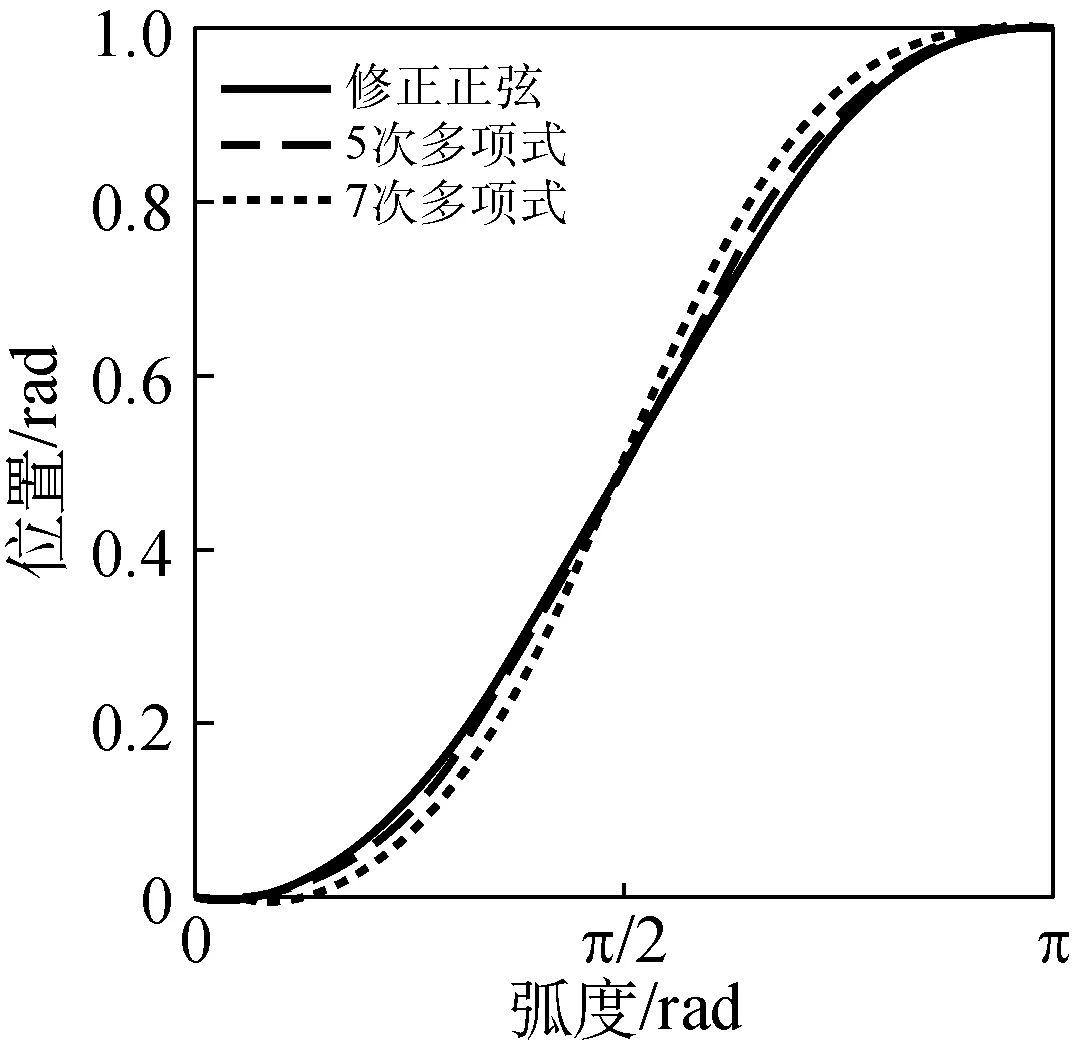
(a) 凸轮位置曲线
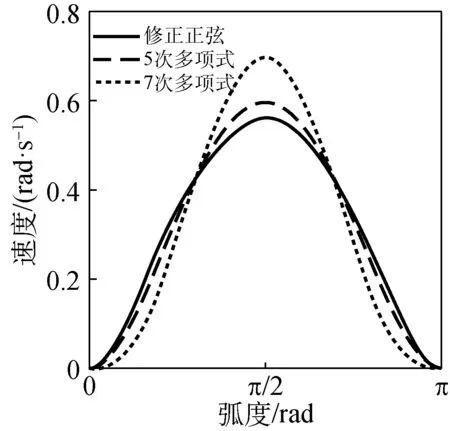
(b) 凸轮速度曲线
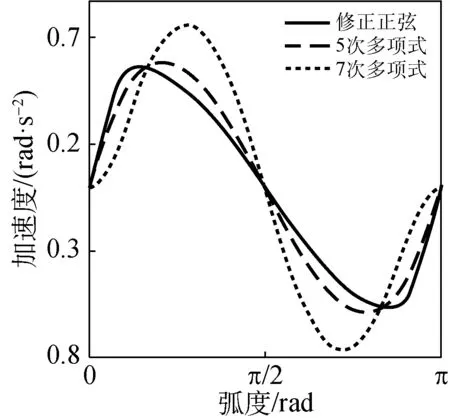
(c) 凸轮加速度曲线
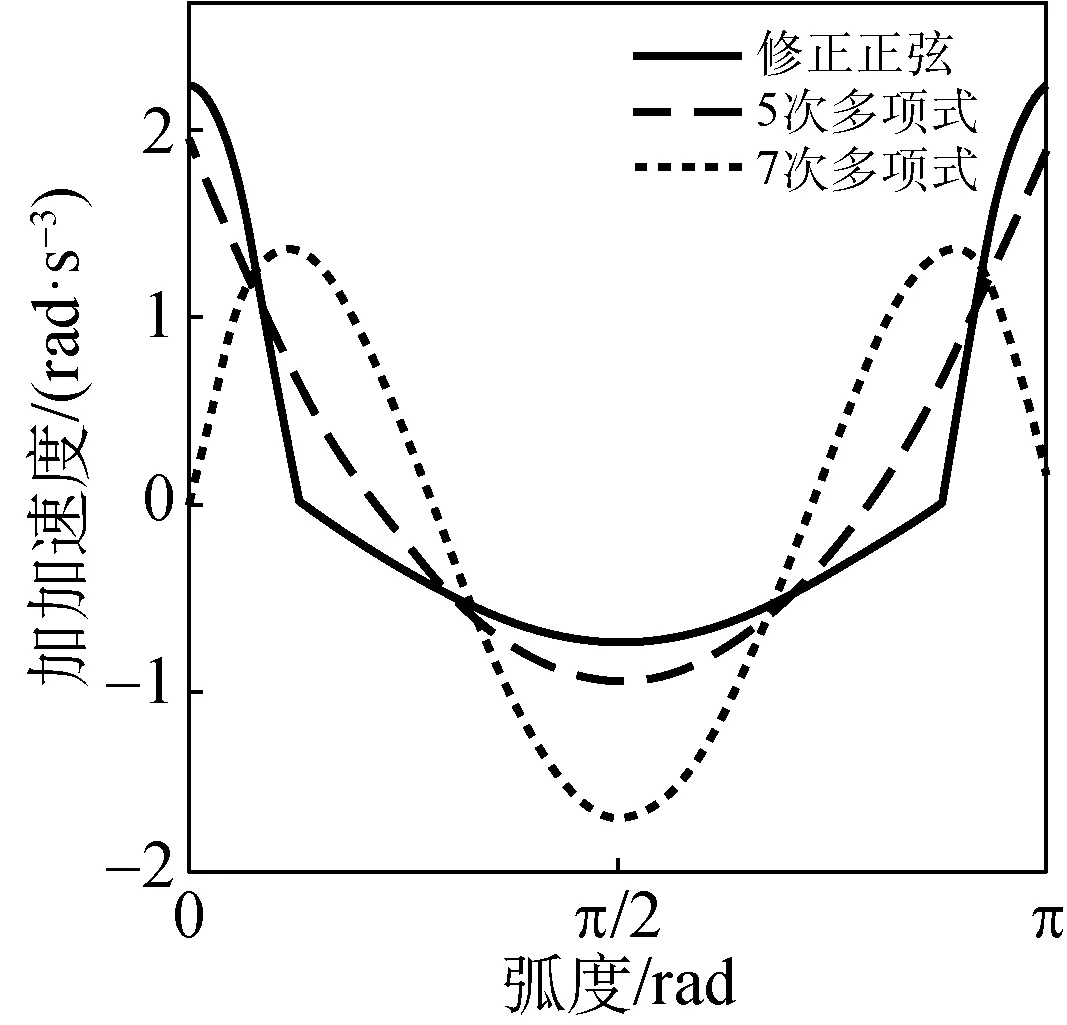
(d) 凸轮加加速度曲线
由图2(b)和(c)可知,修正正弦、5次多项式和7次多项式的凸轮速度和加速度曲线在整个周期内都未发生突变,因此它们都不存在刚性冲击和柔性冲击,但是在接近曲线末端位置时,7次多项式的速度和加速度最小,而修正正弦曲线的速度和加速度最大。对于经编机,梳栉在高速横移运动结束段,驱动电机在大加速度值的减速停止阶段会表现出明显的超调和震荡,系统的位置定位精度急剧下降[4]。由图2(d)可知,7次多项式的角加加速度在整个周期未发生突变,而修正正弦和5次多项式在起始和终止位置产生突变。对加速度曲线而言,角加加速度发生突变在更高程度上就是一种“冲击”[8]。因此,3种凸轮曲线中,7次多项式曲线的性能最好,其次是5次多项式曲线,最后是修正正弦曲线。
由图2(c)可知,从动件运行相同位移时,7次多项式的最大加速度值最大,修正正弦曲线的最大加速度值最小。如果只考虑凸轮曲线性能有可能会由于加速度较大,造成横移伺服的过载。因此在选择凸轮曲线时必须考虑横移伺服电机的性能,同时有必要设计一个算法用以保证横移伺服的最大加速度不超过允许值。
主轴转速决定横移伺服的运动时间,移针量决定横移伺服的位移,因此,影响横移伺服加速度的主要因素为移针量和主轴转速。移针量越大,横移伺服所需的加速度越大;主轴转速越大,横移伺服所需的加速度也越大。当横移伺服所需加速度较大时可选择加速度特征值较小的曲线,如修正正弦曲线;当横移伺服所需加速度较小时可选择加速度特征值较大的曲线,如7次多项式曲线。
2 模糊电子凸轮曲线控制器的设计
本文引进模糊控制算法,根据不同工艺和主轴转速实时选择不同的电子凸轮曲线。模糊电子凸轮曲线控制器的输入为移针量(N)和主轴转速(n),根据不同N和n,经模糊推理得到输出变量为a,而a的大小反映了加速度的大小,再根据a的大小来选择凸轮曲线的类型,最后对电子凸轮曲线进行在线修改和调整。模糊电子凸轮曲线控制结构如图3所示。
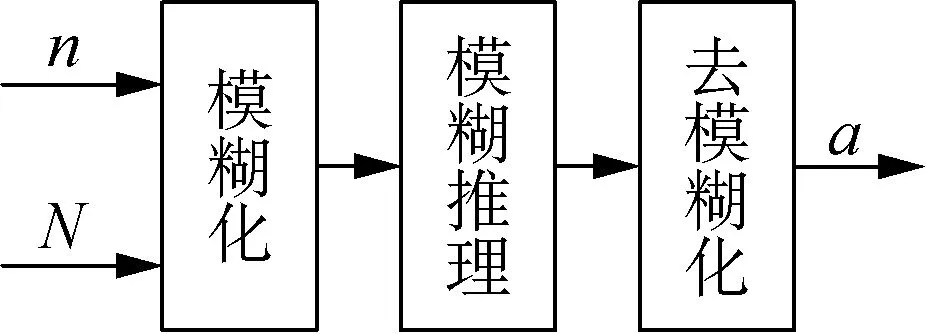
图3 模糊电子凸轮曲线控制结构图Fig.3 Fuzzy electronic cam curve control structure
2.1 模糊电子凸轮曲线控制参数模糊论域
虽然移针量和主轴转速共同影响横移伺服加速度,但由预试验得知:当移针量小于4时,即使主轴转速达到最大值1 000 r/min,采用7次多项式凸轮曲线的加速度仍满足要求;当主轴转速小于850 r/min时,即使移针量达到最大值6,采用7次多项式凸轮曲线的加速度也仍满足要求。模糊论域参数范围如图4所示。由图4可知:当移针量或主轴转速处于非混合区域时,即使采用7次多项式凸轮曲线,加速度仍满足要求,此时可直接选择7次多项式作为电子凸轮曲线;当移针量和主轴转速处于混合区域时,需采用模糊控制器来确定凸轮曲线类型。
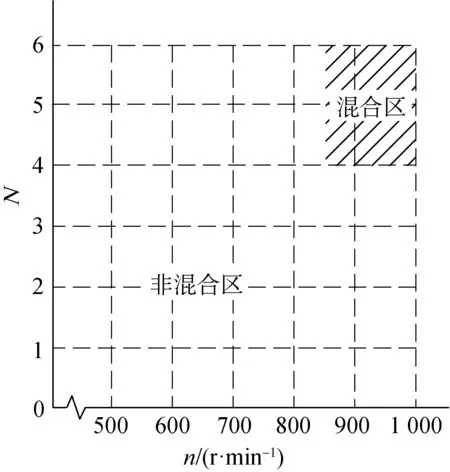
图4 模糊论域参数范围Fig.4 Range of parameters in fuzzy domain
为方便表示,使用语言子集{NB, NS, ZO, PS, PB}分别表示模糊论域子集{“负大”,“负小”,“零”,“正小”,“正大”}。由图4的混合区可知:移针量N的模糊论域设定为[4, 6],且只能为整数,将N的模糊论域定义为3个语言子集,即N={NB, ZO, PB};主轴转速n的模糊论域设定为[850, 1 000],其在区间内连续变化,将n的模糊论域定义为4个语言子集,即n={NB, NS, PS, PB}。规定模糊控制器的输出a的模糊论域为[0, 1],将a的模糊论域定义为3个语言子集,即a={NB, ZO, PB},当a∈{NB}时选择修正正弦曲线,当a∈{ZO}时选择5次多项式曲线,当a∈{PB}时选择7次多项式曲线。选择三角隶属函数对上述模糊电子凸轮曲线控制器的输入和输出变量的模糊集合进行描述,如图5所示。
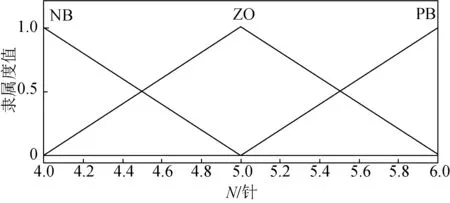
(a) 移针量N隶属度函数曲线
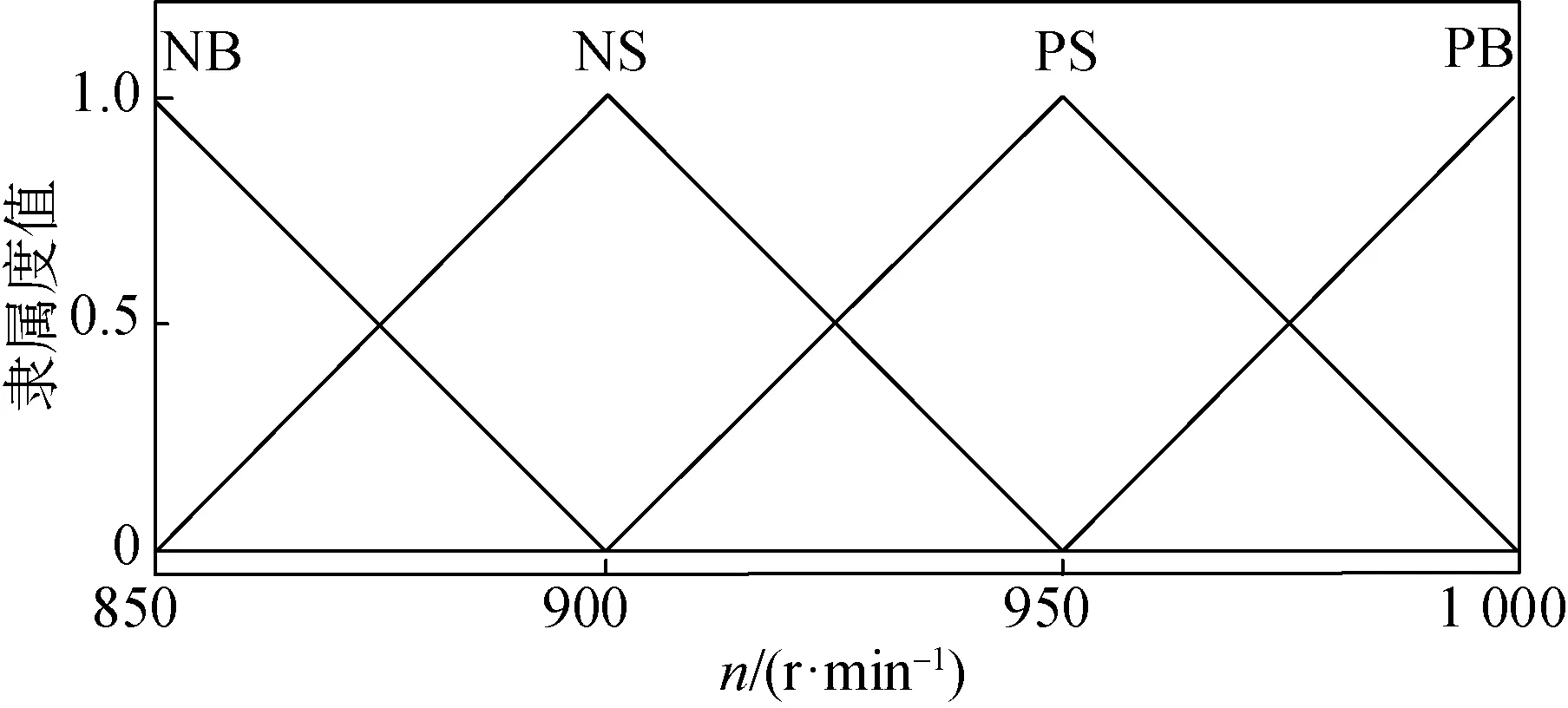
(b) 主轴转速n隶属度函数曲线
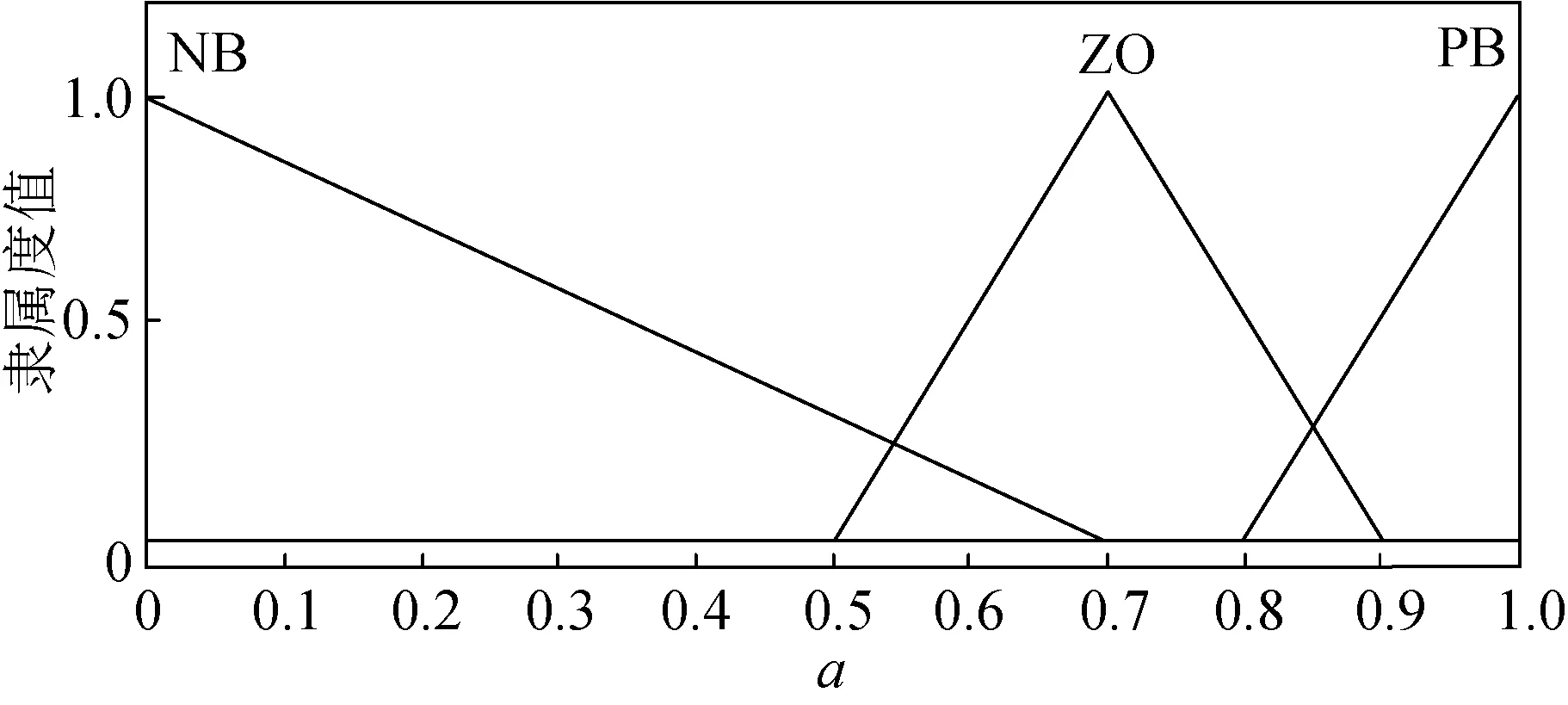
(c) a隶属度函数曲线
2.2 模糊控制规则表的确立
为建立模糊控制规则,采用基于BECKHOFF公司的TwinCAT软件对电子横移进行仿真。梳栉摆动对应的主轴角度采用表2所示。编织工艺采用表3所示工艺,其中数字表示电子横移的移针量,该工艺可同时模拟移针量为1~6的情况。分别对采用不同电子凸轮曲线,主轴转速为850、900、950和1 000 r/min时横移伺服的位置、速度、加速度进行仿真。以主轴转速为900 r/min,采用5次多项式时的仿真结果如图6所示。由图6可知,当移针量为6时,仿真得到的最大加速度为1.396×106(°)/s2,即2.436×104rad/s2,未超过横移伺服的最大理论加速度。因此对于主轴转速为900 r/min,移针量为6时,可以选择5次多项式曲线作为经编机电子横移的电子凸轮曲线。根据图5所示的输入及输出隶属度曲线可知,主轴转速为900 r/min对应的语言子集为{NS},移针量6对应的语言子集为{PB},而选择5次多项式曲线时模糊控制器的输出变量a对应的语言子集为{ZO},由此可得到一条模糊控制规则,即当n∈{NS},N∈{PB}时,输出变量a∈{ZO}。根据所有仿真结果得到的模糊控制规则,如表4所示。

表2 GB1梳栉摆动对应的主轴角度

表3 GB1试验编织工艺(移针量)

表4 模糊控制规则
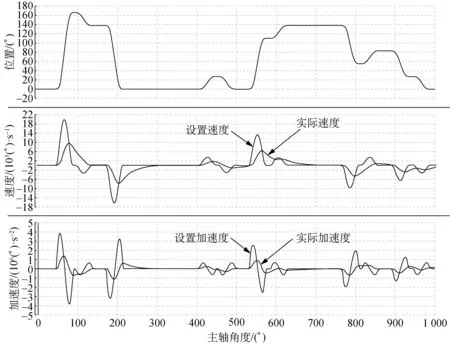
图6 5次多项式仿真结果Fig.6 Five-degree polynomial simulation results
根据参数的模糊论域和模糊控制规则,利用Matlab软件内置的模糊控制器进行仿真,得到如图7所示的结果。由图7可知,不同的移针量和不同的主轴转速对应唯一的a值,而a值反映了加速度的大小。因此可根据模糊控制器输出的a值,来选择合适的凸轮曲线。
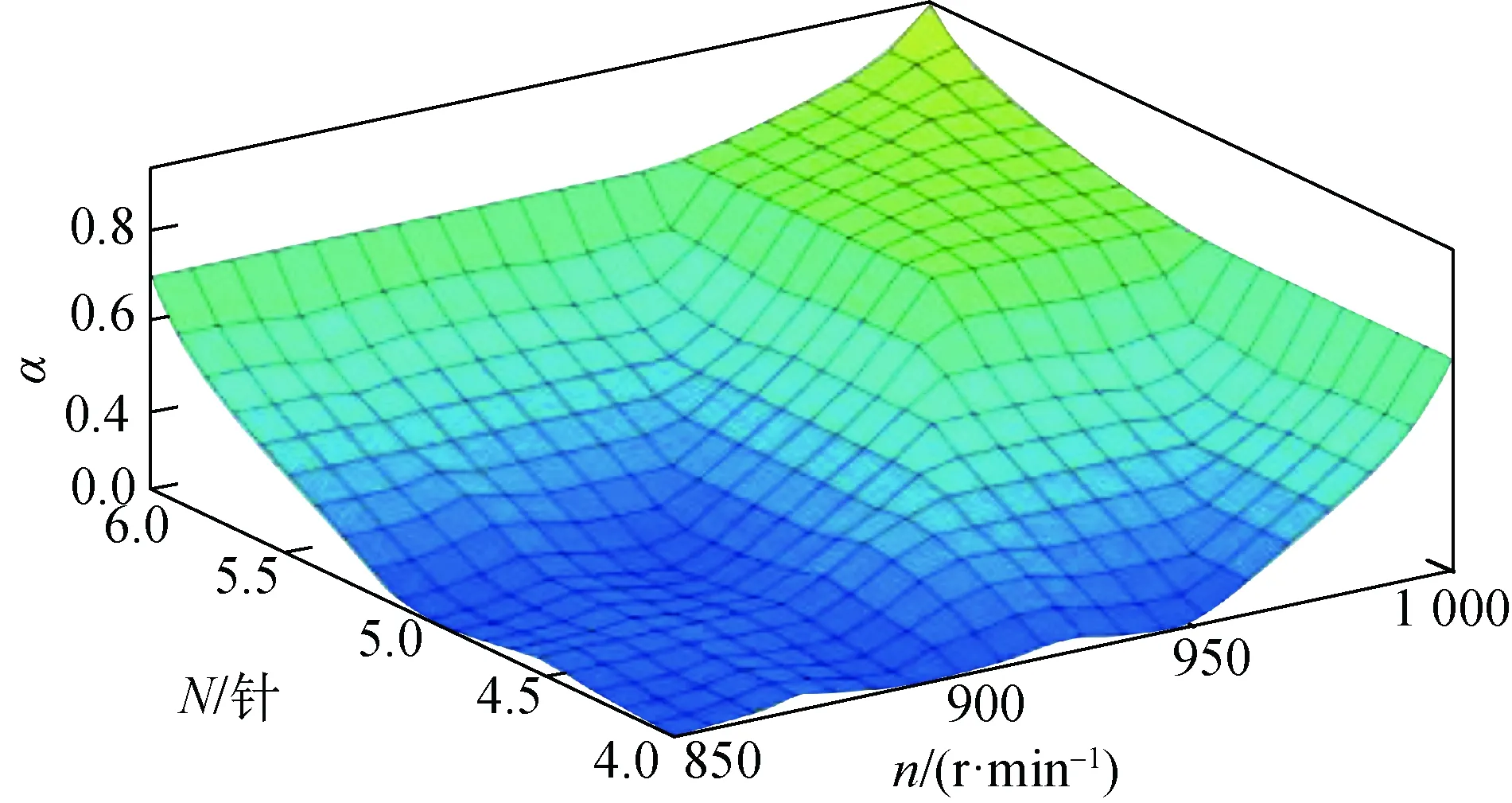
图7 模糊控制器的Matlab仿真结果Fig.7 Matlab simulation results of the fuzzy controller
2.3 基于模糊电子凸轮曲线的电子横移控制算法流程
基于模糊电子凸轮曲线的电子横移控制算法基于BECKHOFF的CX5120型控制器实现,程序首先对用户输入的主轴转速和读取的每一横列的编制工艺进行判断,判断是否处于混合区。对处于混合区的参数进行模糊化,经模糊推理和解模糊后根据模糊控制器输出的加速度选择合适的电子凸轮曲线,对不处于混合区的直接选择性能最优的7次多项式曲线。对生成的凸轮位置点进行存储,同时对电子横移伺服和主轴进行耦合。此时可启动主轴,凸轮曲线选择当前工艺的第一横列所生成的凸轮曲线。当主轴开始旋转后,在线修改凸轮的曲线为下一横列曲线,同时设置为下一周期生效。如此循环直至编织布长达到设定布长,关闭主轴,结束编织。算法流程图如图8所示。
3 控制系统动态响应测试与分析
为验证模糊电子凸轮曲线控制规则的合理性和有效性,利用BECKHOFF公司的TwinCAT软件进行仿真测试。编织工艺采用表5所示工艺,主轴转速设置为1 000 r/min,分别对采用模糊电子凸轮曲线的控制系统和未采用模糊电子凸轮曲线的控制系统进行仿真。
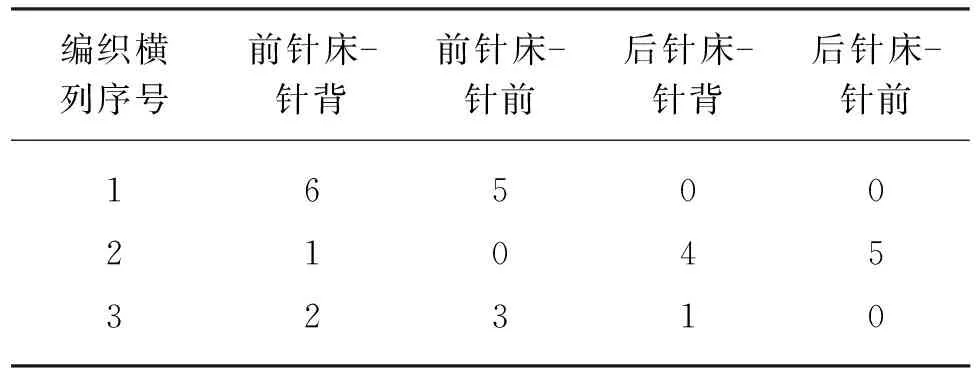
表5 GB1实验编织工艺(移针量)
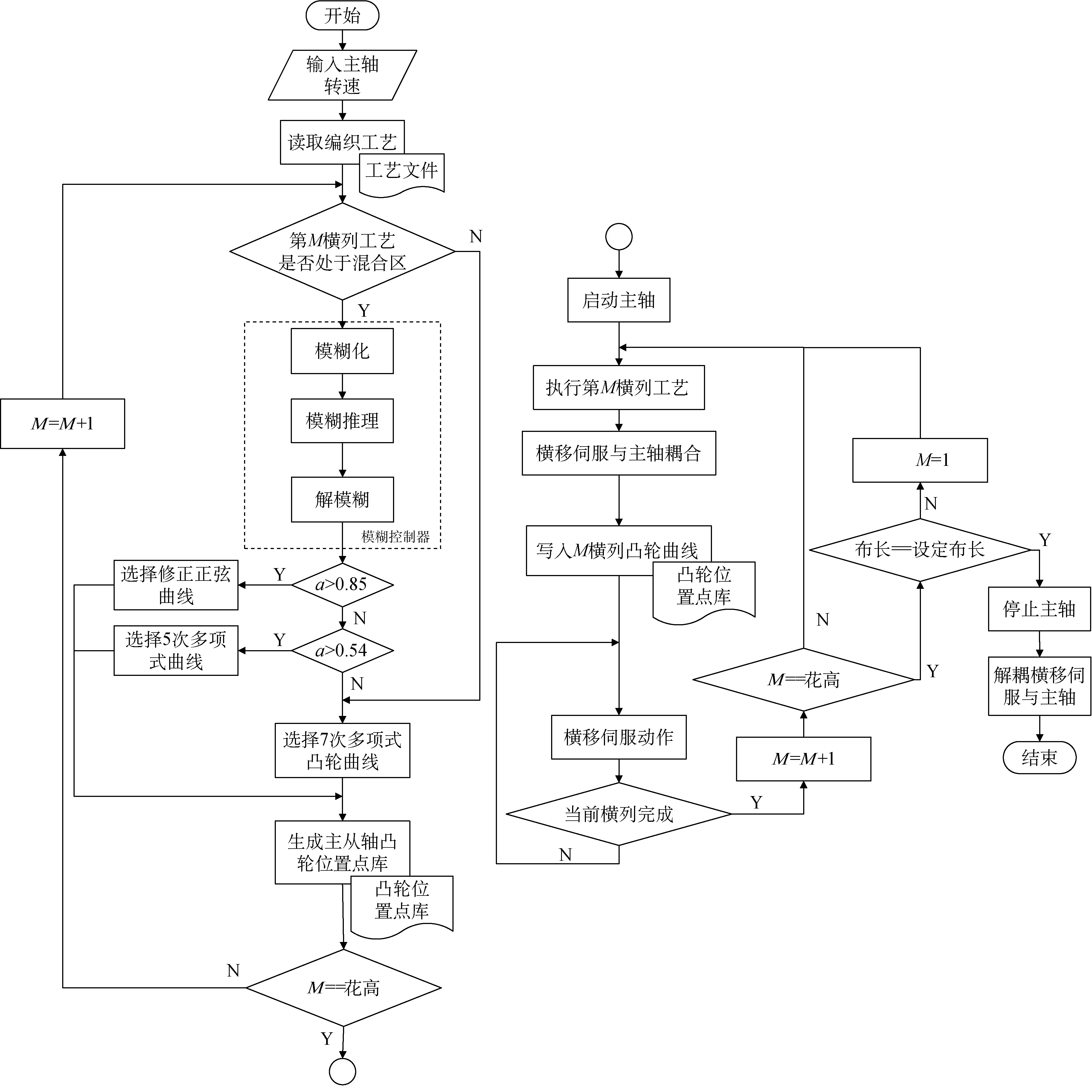
图8 基于模糊电子凸轮曲线的电子横移控制算法流程图Fig.8 Flow chart of electronic shogging control algorithm based on fuzzy electronic cam curve
图9和10分别为采用和未采用模糊电子凸轮曲线的仿真结果,可反映电子横移的移针量。例如,当横移伺服的位置由0°变为165°时,横移伺服的移针量为6针。由图9可知:采用模糊控制的经编机电子横移控制系统,当移针量为6时,选择修正正弦曲线,移针量为5时,选择5次多项式曲线,其余则选择7次多项式曲线;仿真得到的最大实际加速度为1.435×106(°)/s2,即2.505×104rad/s2,小于所选伺服的理论最大加速度。由图10可知,未采用模糊控制的经编机电子横移控制系统,全部采用7次多项式曲线,仿真得到的最大实际加速度为1.847×106(°)/s2,即3.224×104rad/s2,远远超出所选伺服的理论最大加速度,在实际应用中会造成横移伺服的过载。
4 结 论
(1) 修正正弦曲线、5次多项式曲线、7次多项式曲线都满足速度、加速度连续,即没有柔性冲击,均适合作为经编机主轴与横移伺服运动耦合的电子凸轮曲线。
(2) 仿真分析可知,经编机电子横移的应用中,相同条件下,不同电子凸轮曲线的实际最大加速度由大到小依次为7次多项式曲线、5次多项式曲线和修正正弦曲线。
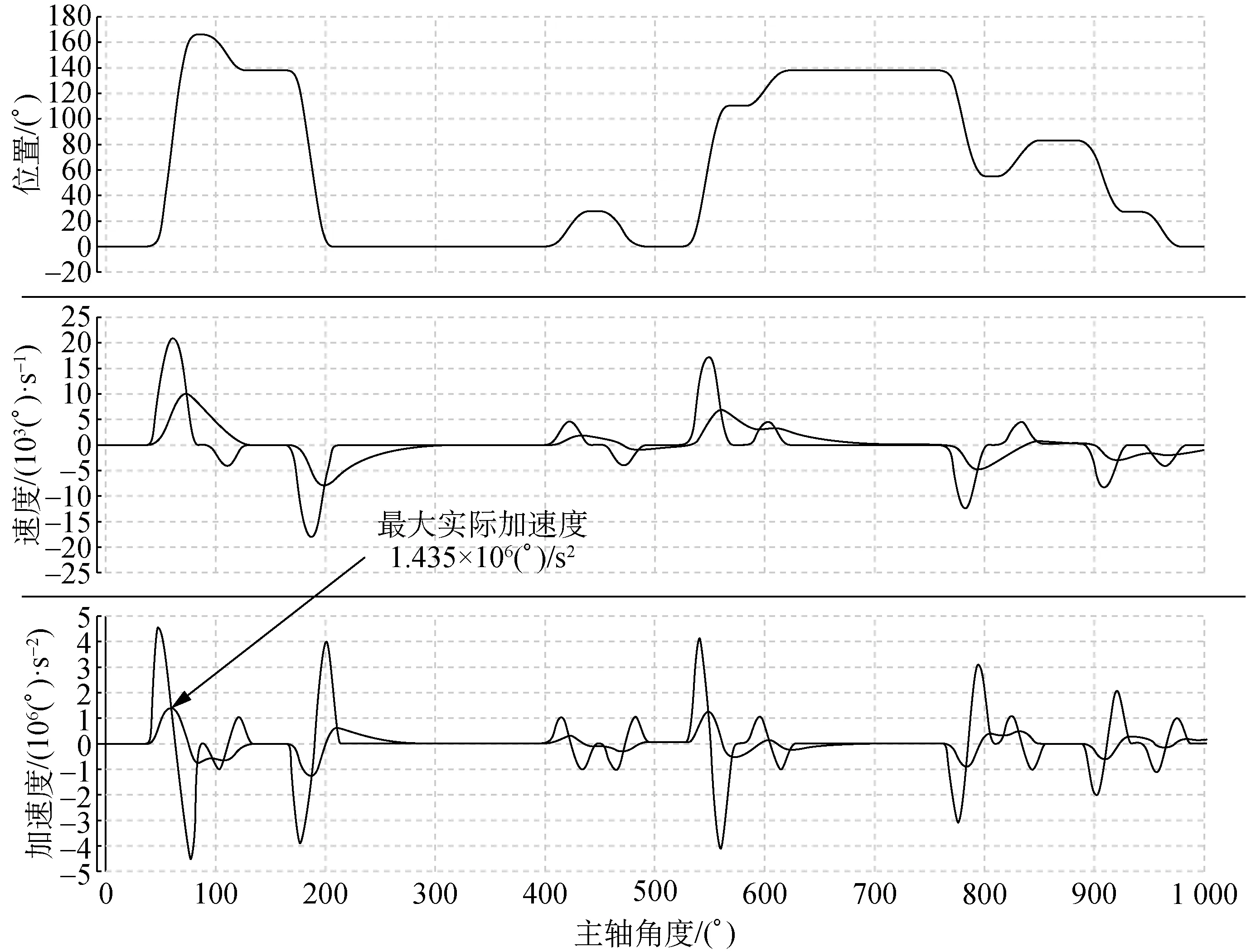
图9 采用模糊电子凸轮曲线得到的仿真结果Fig.9 Simulation results obtained by using fuzzy electronic cam curve
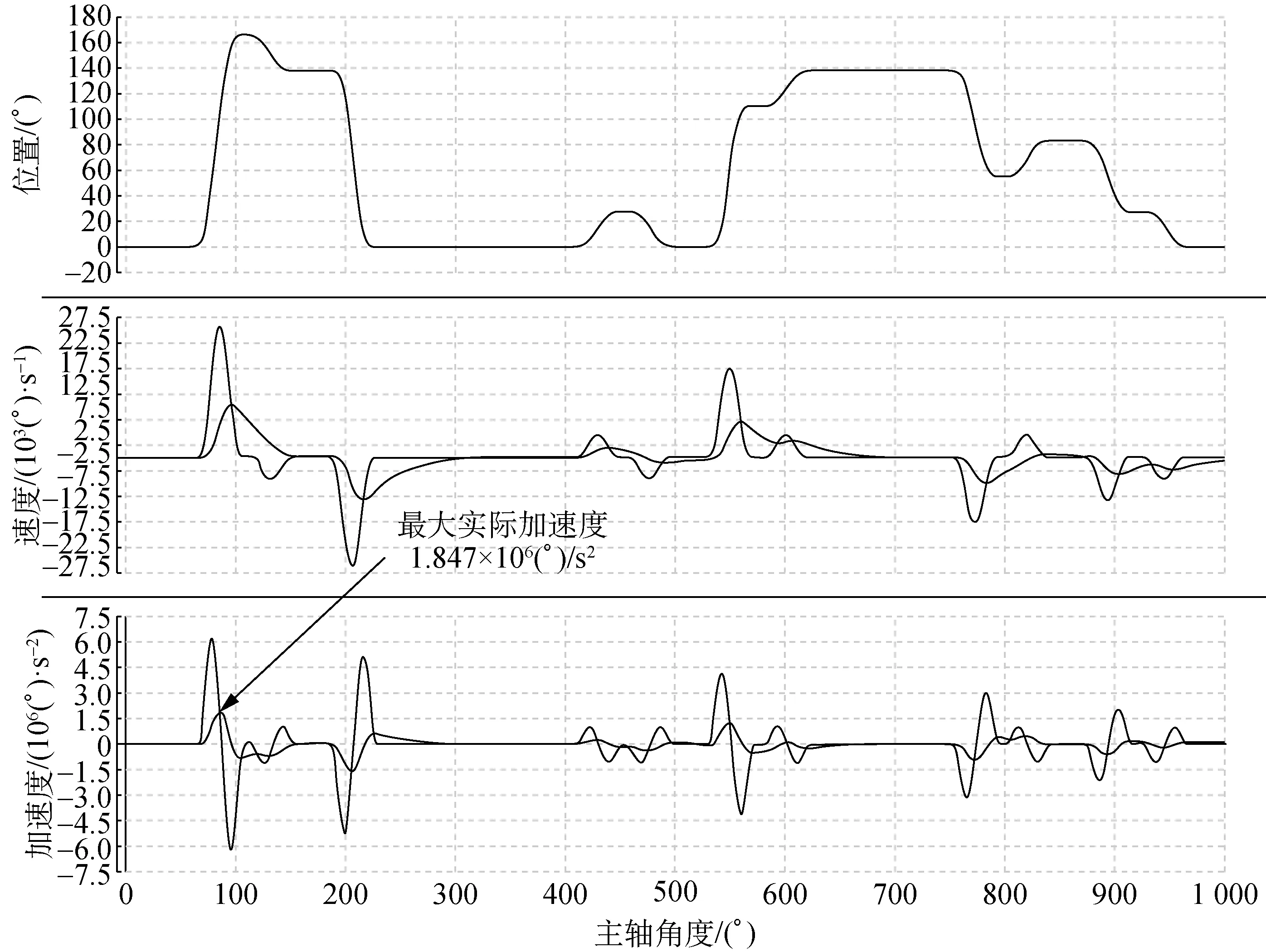
图10 未采用模糊电子凸轮曲线得到的仿真结果Fig.10 Simulation results obtained without using fuzzy electronic cam curve
(3) 采用模糊电子凸轮曲线控制的电子横移控制系统可根据主轴转速和移针量实时自动选择不同的电子凸轮曲线,同时可在横移伺服性能允许的前提下选择性能最优的电子凸轮曲线。
