应力回复对PVC膜材应力松弛行为的影响
2020-12-02汪泽幸朱文佳
汪泽幸,吴 波,朱文佳,何 斌,刘 超
(1. 湖南工程学院 纺织服装学院,湖南 湘潭 411104;2. 湖南省新型纤维面料及加工工程技术研究中心,湖南 益阳 413000)
膜材通常以聚酯纤维或玻璃纤维织物为增强体,以聚氯乙烯(polyvinyl chloride,PVC)、聚四氟乙烯(polytetrafluoroethylene,PTFE)、聚偏氟乙烯(polyvinylidene fluoride,PVDF)等为基体,采用涂层加工方式制备而成[1-2]。作为一种具有明显非弹性、非线性、黏弹性且具有正交各向异性特征的柔性复合材料,其黏弹性以蠕变和应力松弛的形式展现出来。应力松弛过程中,因材料内部结构的调整,导致材料内部的应力持续降低,虽应力松弛不会引起膜材的宏观破坏,但会导致膜结构表面整体刚度降低,在强风作用下引起膜结构表面出现大幅度的反复摆动,最终引起膜材的撕裂破坏[3]。为避免使用过程中膜结构表面的张力过度损失,需定期进行张力检测,并根据需要对膜结构表面的张力进行调整。
膜材作为一种具有显著黏弹特性的工程材料,其力学行为不仅与所受的应力状态相关,还与加载历史密切相关。为全面研究以膜材为代表的织物增强类柔性复合材料的应力松弛行为,众多学者对PVC膜材[4-8]、PTFE膜材[7, 9-11]及其他涂层织物类柔性复合材料[12-13]在不同条件下的应力松弛行为及其描述模型进行了研究,但这些均在应力松弛前无应变或应力回复历史条件下进行。
现有研究表明,高聚物[14-16]、纤维[17-18]、纱线[19-23]、织物[23-24]、复合材料[25]等具有回复滞后的材料,应力松弛前如有应变或应力回复历史,应力松弛过程中试样中的应力将呈非持续衰减趋势,即表现为非寻常的应力松弛行为。根据应力与松弛时间之间的变化规律,将应力松弛行为可分为3类[26],即简单应力松弛行为、混合应力松弛行为与逆应力松弛行为。文献[22]认为醋酸长丝和涤纶长丝的应力松弛行为可采用基于多个Maxwell单元串联的广义元件模型来描述,但未对模型合理性进行验证。文献[23-24]通过将1个定参数弹簧元件与2个定参数Maxwell单元并联构建了5元件模型,阐述了逆应力松弛和混合应力松弛现象的产生机理,并对纤维、纱线等的逆应力松弛行为进行了拟合分析,但未验证描述混合应力松弛和简单应力松弛时的拟合精度。文献[26-27]基于定参数弹簧和分数阶导数元件构建了分层模型,该模型可较好地描述聚乙烯树脂的简单应力松弛行为,而对混合应力松弛与逆应力松弛行为的拟合效果较差。文献[14-15]基于半结晶聚合物的黏弹性和黏塑性响应行为构建了两相模型,该模型能较好地描述聚丙烯树脂的简单应力松弛、混合应力松弛及逆应力松弛行为,但由于本构方程含有复杂的积分项,计算过程繁琐,使用不便。文献[16]基于聚合物过应力模型对聚丙烯的短时混合应力松弛行为进行了模拟分析,但未对简单应力松弛和逆应力松弛行为进行拟合分析。
基于此,为深入研究膜材在复杂受力历史条件下的力学行为,以商购PVC膜材为研究对象,对其应力回复后的应力松弛行为进行测试和分析,基于非线性黏弹性元件建立双变参数元件模型,并分析模型描述该膜材应力松弛行为的适宜性。
1 试验材料与方法
以商购施恩特PVC膜材为试验对象,其表层涂覆PVDF为耐气候层,实测膜材厚度为0.72 mm。试样为长300 mm、宽50 mm的矩形试样,有效夹持隔距L0为200 mm,两端夹持部位均采用高强黏合剂黏合不锈钢薄片加以保护。
膜结构施工过程中,预加张力通常采用单位宽度内膜材上施加的载荷来表示,且在研究膜材的应力松弛行为时亦可在设定初始张力的条件下进行[4-5, 7, 9-11],同时,为确保试验过程中试样始终处于拉伸状态,本文采用应力控制方式对膜材的应力松弛行为进行测试。
试样应力回复后的应力松弛代表性试验过程如图1所示。其中,OA曲线段,试样以10 mm/min的拉伸速率v历经时间t1(s)加载至最大应力σmax(N/mm),然后以同等速率v历经时间(t2-t1)卸载至初始松弛应力σ0(如AB曲线段所示),保持σ0对应的应变ε0,保持时间t*(t*=t-t2)为14 400 s(如BC曲线段所示)。
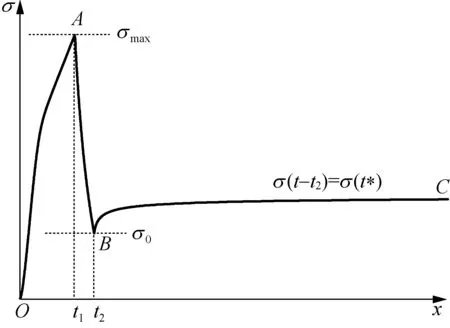
图1 代表性试验过程曲线Fig.1 Representative total testing curve
所有试验均在WDW-20C型微机控制电子试验机上进行,环境温度为25 ℃,有效试验样本数为3,以代表性应力松弛曲线为后续分析对象。
2 结果与讨论
2.1 应力松弛行为分析
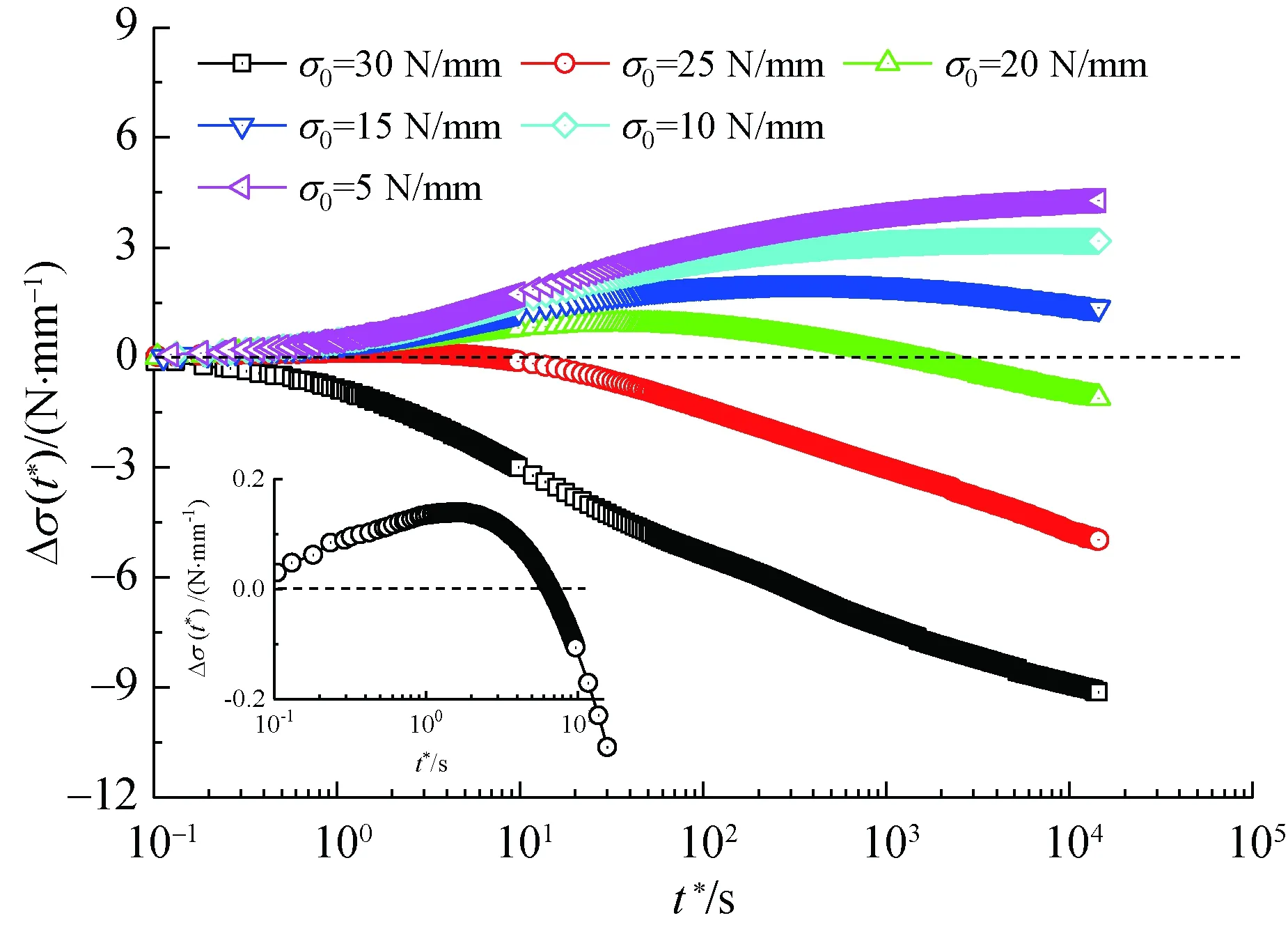
应力松弛前最大应力σmax为30 N/mm,不同初始松弛应力σ0时,膜材经、纬向试样的应力松弛曲线如图2所示。由图2可知,观测时间内,膜材经、纬向试样均表现出3种形式的应力松弛行为:(1)当应力松弛前无应力回复历史时,即应力回复量σ(σ=σmax-σ0)为0,膜材表现出简单应力松弛行为,应力随松弛时间的增加而持续减小;(2)应力回复量较大时,随松弛时间的增加,应力呈逐渐增大的趋势,即表现出明显的逆应力松弛行为;(3)应力回复量较小时,随松弛时间的增加,应力呈先增大后减小的趋势,即表现出混合应力松弛行为。
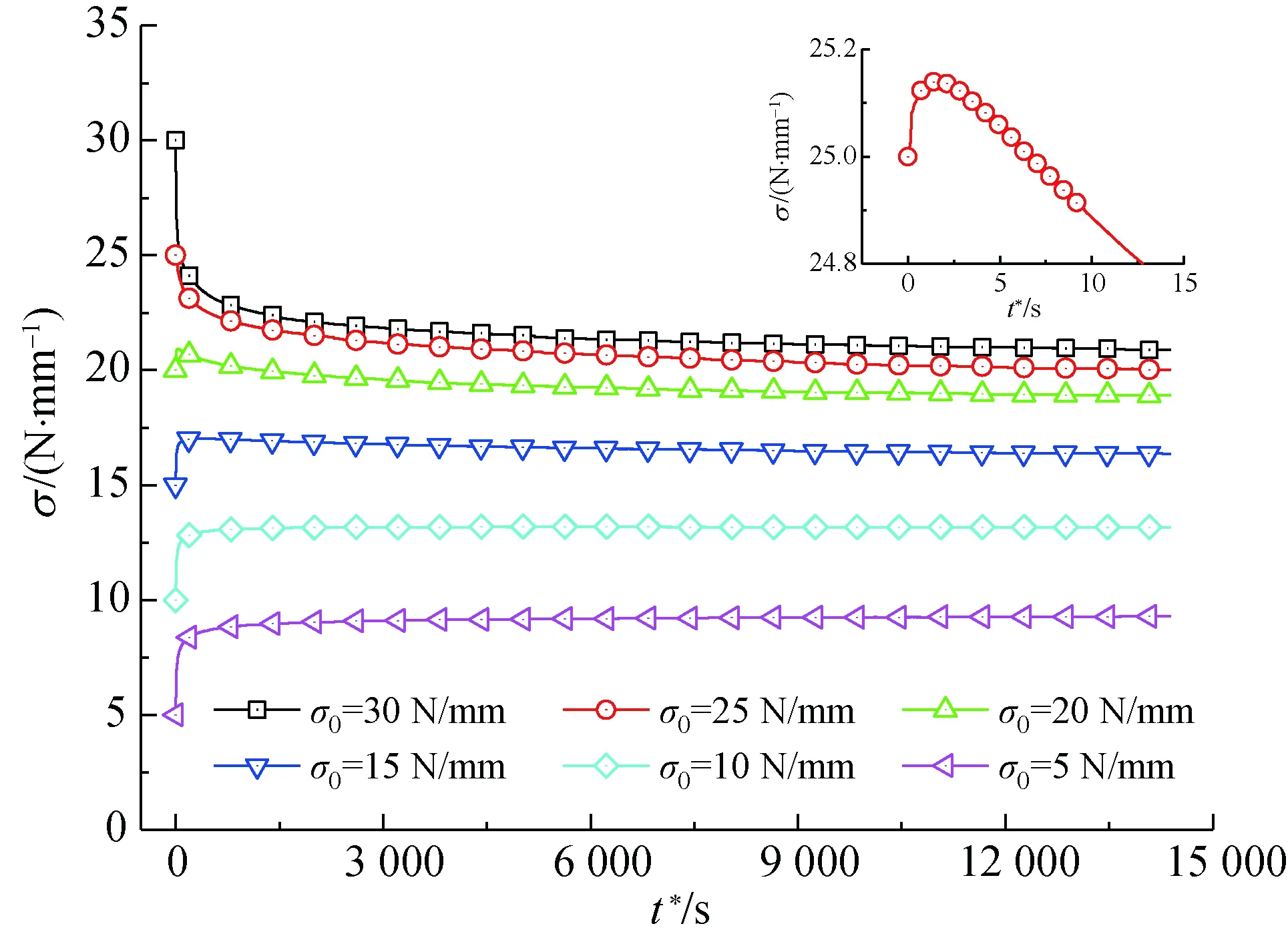
(a) 经向
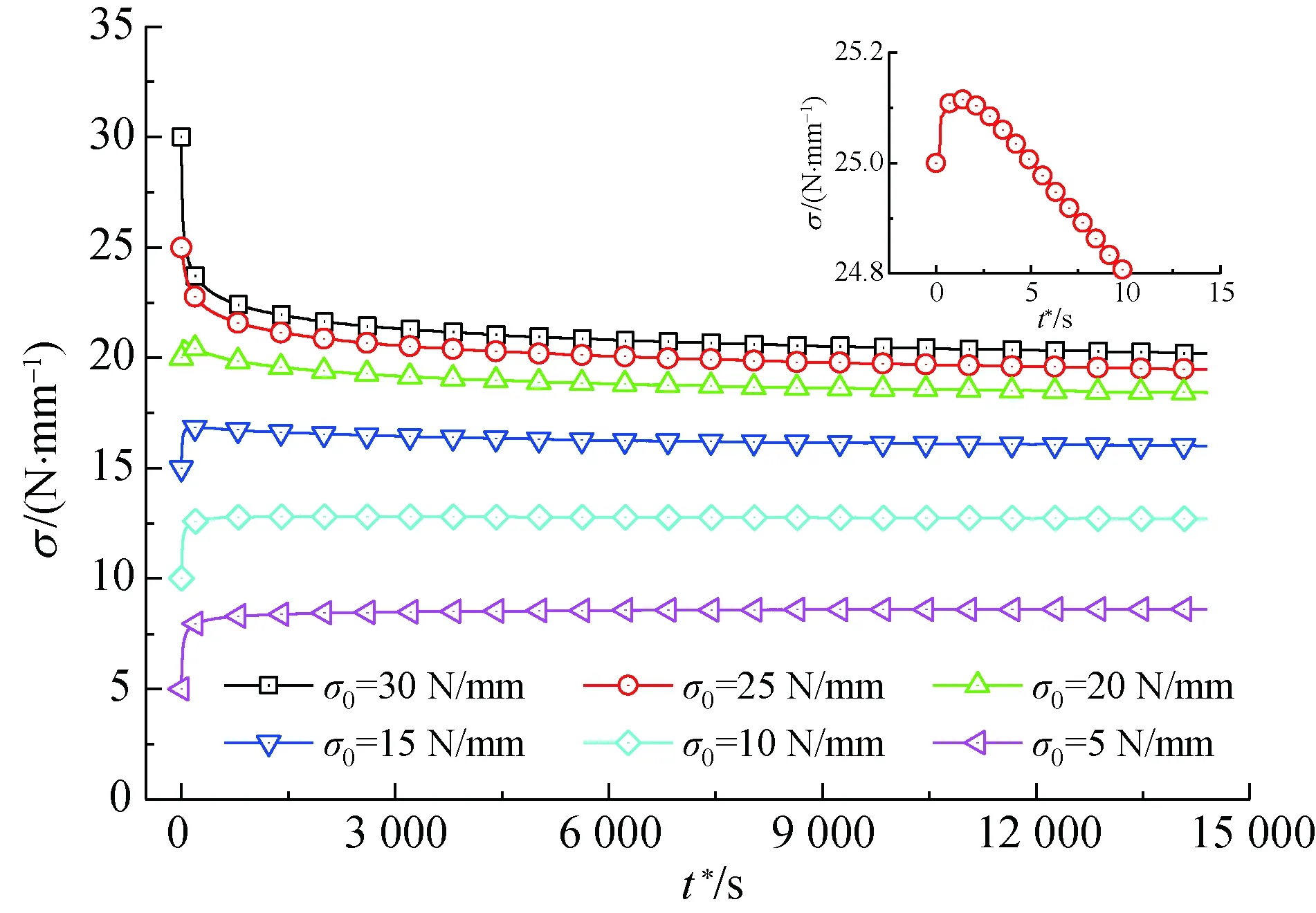
(b) 纬向
试样处于等速拉伸阶段(图1中OA曲线段)时,随着加载的进行,增强体纤维和表层涂覆材料的大分子链伸长,且与其他大分子链结合较弱的大分子链被拆散,此时产生相对滑移并在新的位置上建立连接,所有大分子链均处于拉伸状态,且增强体纤维与涂覆高分子材料之间出现脱黏现象,从而产生不可逆的塑性变形。
应力松弛前无应力回复历史时,松弛过程中增强体和涂覆层大分子链均处于拉伸状态,大分子链通过键角与键长改变、分子链构象调整、分子链滑移与重排等方式实现大分子构型的平衡,材料内部残余应力逐渐降低并趋于恒定,材料表现为简单应力松弛行为。
当应力松弛前存在应力回复时,随着外加应力的减少,原有拉伸状态的大分子链在内应力作用下向内回缩。当外加应力回复至初始松弛应力时,控制初始松弛应力对应的应变,但此时增强体纤维和涂覆层高分子材料的大分子链变形并未停止,由于增强体纤维和涂覆层高分子的长链结构和大分子运动的逐步性,大分子链在受外力作用时与外力相适应的形变不可能在瞬间完成,大分子链向内收缩和重排运动将继续进行,并通过大分子链构象和重排直至与对应保持应变相适应的平衡态,而达到此平衡态所需的时间与初始松弛应力对应应变状态时大分子链间的作用力相关。在大分子链回缩过程中,拉伸阶段产生相对滑移与未产生滑移大分子链承受的内应力不同,在回缩过程中回缩速率存在差异,产生相对滑移的大分子链将对未滑移大分子链的回缩运动产生阻碍作用,同时,大滑移量大分子链也将对小滑移量大分子链的回缩也将起到阻碍作用,延迟大分子的向内收缩和大分子的重排运动。当应力回复量较小时,大分子链之间的阻碍作用对大分子回缩影响较小,大分子链的构象和重排可短时间内达到平衡,之后再通过大分子链的键角与键长改变、分子链构象调整等实现内应力的逐步降低,大分子链整体呈先收缩后拉伸的变化过程,宏观表现为材料内应力呈先增加后减小的变化趋势,即混合应力松弛行为。随着应力回复量的增加时,大分子链之间的阻碍作用对大分子回缩造成的影响程度逐渐增加,大分子链构象和重排达到平衡状态所需的时间也逐渐增加,当应力回复量达到某一阈值时,大分子链将始终保持收缩状态,宏观表现为材料内应力呈现持续增加的变化趋势,即逆应力松弛行为。
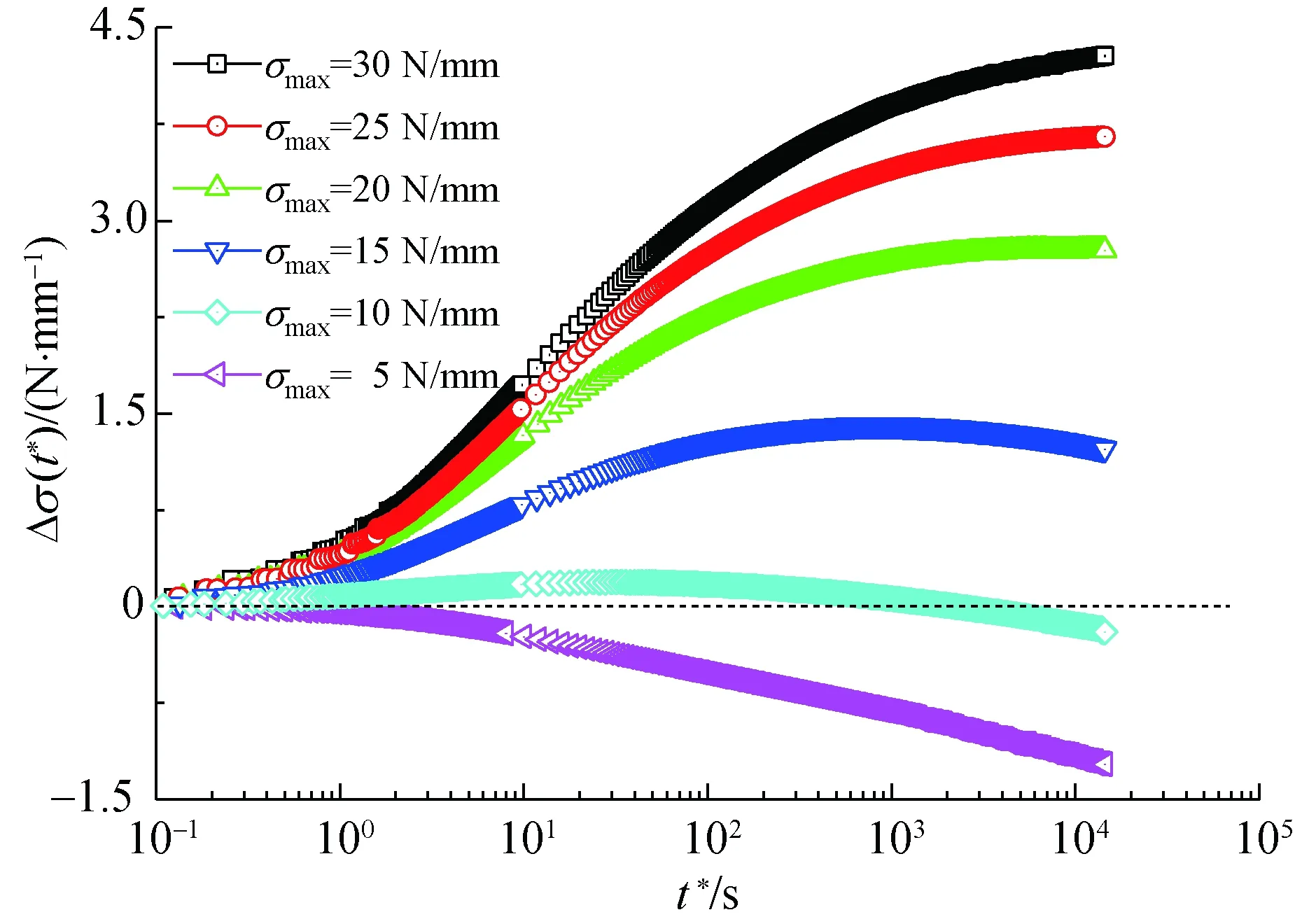
从图2还可以看出,PVC膜材经、纬向试样的应力松弛曲线的形态高度相似,表明PVC膜材经、纬向试样的应力松弛机理一致。基于此,后续以经向试样为研究对象,对其在初始松弛应力为5 N/ mm时,不同最大应力下的应力松弛行为进行测试,结果如图3所示。
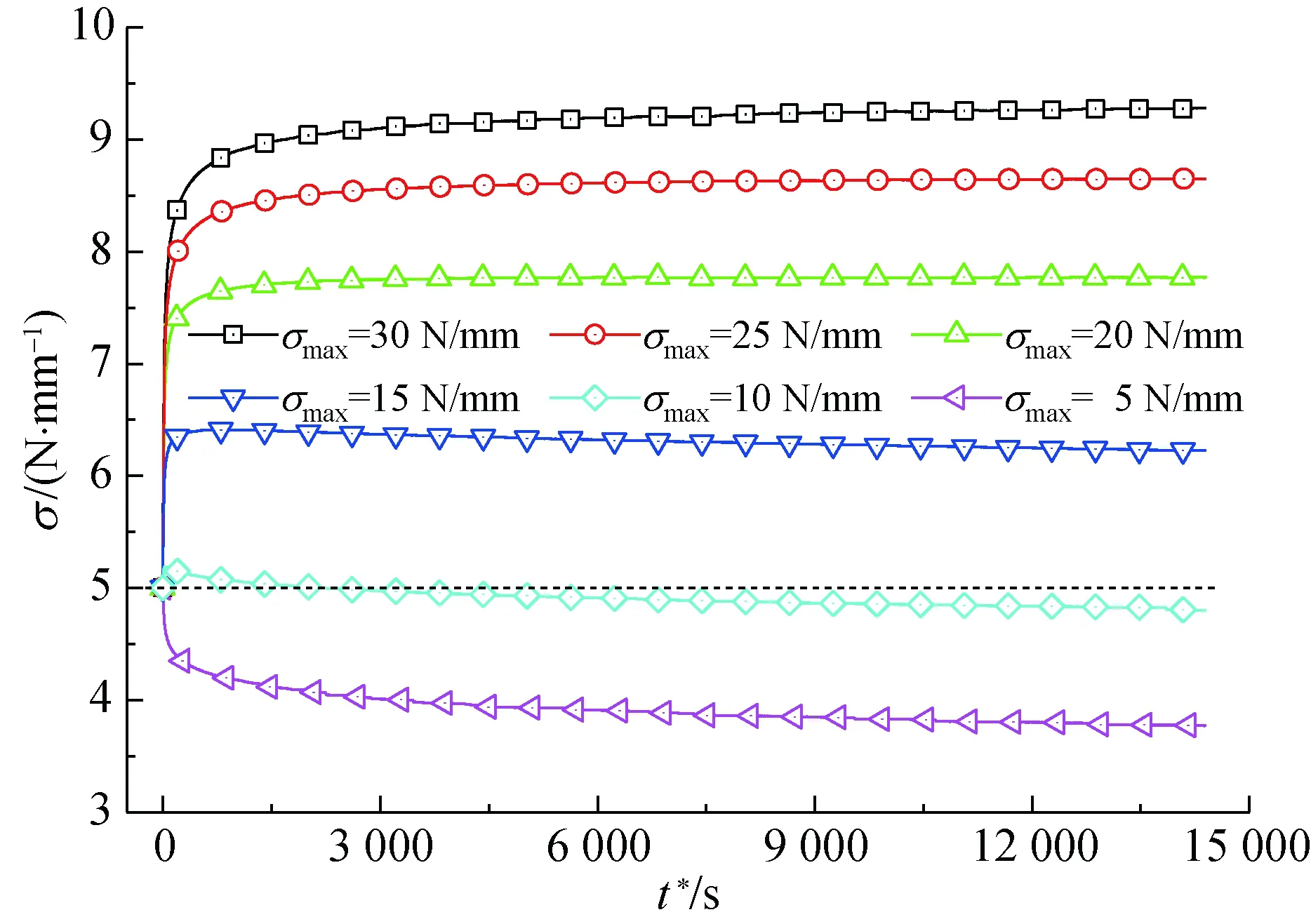
图3 σ0为5 N/mm时经向试样的应力松弛曲线Fig.3 Stress relaxation curves of warp specimens at σ0 of 5 N/mm
从图3可以看出,同等初始松弛应力下,随最大应力增加,即应力回复量的增加,经向试样表现出简单应力松弛、混合应力松弛与逆应力松弛行为。
由图2(a)与图3可知,PVC膜材经向试样的应力松弛行为与松弛前应力回复阶段的最大应力与初始松弛应力密切相关。这主要是由不同最大应力和初始松弛应力条件下,大分子之间作用力以及大分子回复滞后性存在差异所致。
由图2和图3可知,历经不同应力回复历史后的PVC膜材在应力松弛过程中,试样中的应力均不同程度地偏离设定的初始松弛应力,即对初始松弛应力的保持能力存在差异。为研究应力松弛过程中材料对初始松弛应力的保持能力,引入应力变化量σ(t),其可表示为
Δσ(t*)=σ(t*)-σ0
(1)
式中:σ(t)为应力松弛过程中试样所承受的应力,N/ mm。
经向试样的应力变化量曲线以半对数形式绘于图4中。
从图4可以看出,应力松弛前历经应力回复后的试样对初始松弛应力的保持能力明显高于无应力回复试样,且保持能力与应力松弛前最大应力σmax和初始松弛应力σ0的选用密切相关。当σmax=30 N/ mm,σ0=20 N/ mm时,对初始松弛应力的保持能力较好;当σ0=5 N/ mm,σmax=10 N/ mm时,经向试样对初始松弛应力的保持能力较好。
(a) σmax=30 N/ mm
(b) σ0=5 N/ mm
从图2可以看出,虽对膜结构表面施加较高的预加应力,可逐渐松弛到设计应力,但预加应力过大时,在外加载荷作用下膜材会提前进入塑性状态,导致其承载能力降低。因而,对膜材施加的预加应力应小于膜材拉伸强度的5%(通常为1.5%~4.0%)[28],并分步进行施加预加应力,在后期使用过程中定期检测和反复调整。
基于此,利用历经应力回复后PVC膜材对初始应力的保持能力高于无应力回复试样的现象,在膜材施工过程中的膜结构表面预加应力施加阶段,将膜材过度加载并卸载至设定的预加应力,可避免后期使用过程中膜面张力过度损失,从而在较长时间范围内确保膜结构表面张力稳定,延长膜结构表面张力调节的时间间隔,有效降低后期维护工作量。此外,该种方法需要使膜材短期加载至较高载荷并卸载,但相比直接施加较高载荷的方法,高载荷施加的时间较短,可避免膜材过早进入塑性阶段,从而实现膜结构表面维持稳定的目的。
2.2 定参数与变参数应力松弛模型
对Polciene等[22]建立的5元件模型(1个定参数弹簧与2个定参数Maxwell单元并联)中Maxwell单元数量进行拓展,获得广义Maxwell模型,如图5所示。其中:E0、Ei分别为定参数弹簧元件和第i个Maxwell单元中弹簧的弹性模量,N/ mm;ηi为第i个Maxwell单元中黏壶的黏滞系数,N·min/ mm,i=1,2,… ,k。
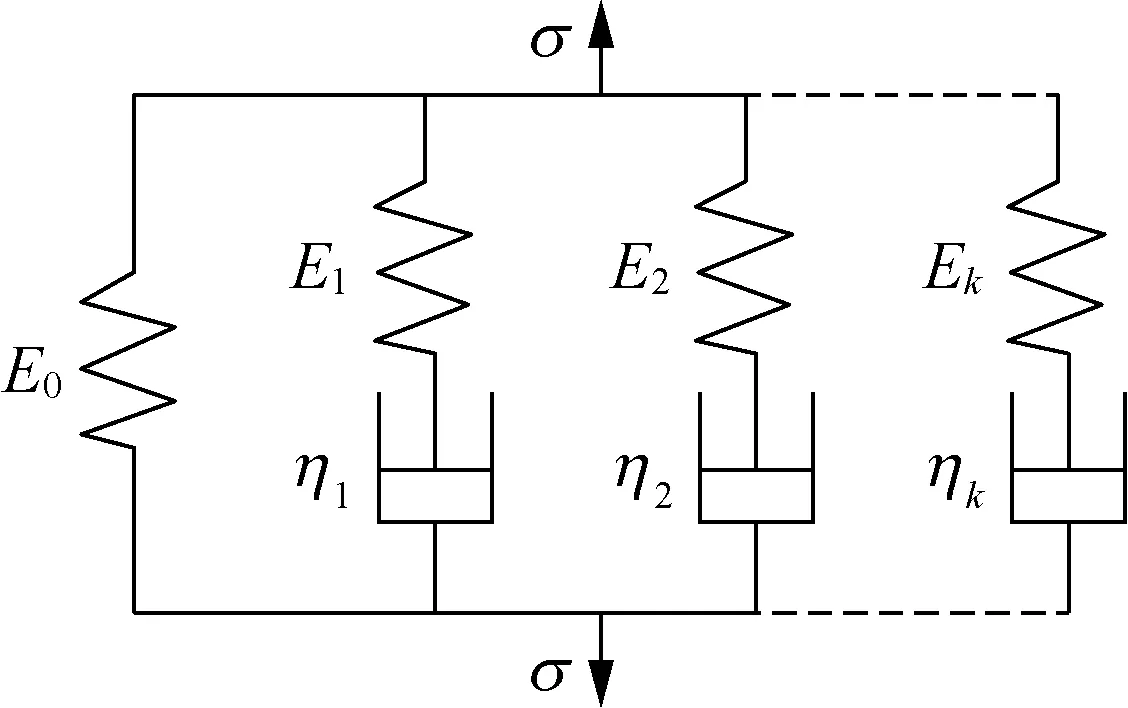
图5 定参数元件模型Fig.5 Constant parameter element model
模型中第i个Maxwell单元的本构方程表达式σi(t)可表示为
(2)
当以速度v等速加载,试样有效夹持长度为L0时,名义应变(t)可表示为
(3)
当模型应变以如式(3)所示的应变加载时,求解式(2)并考虑初始条件σi(t)|t=0=0,则第i个Maxwell单元的本构方程及其应力松弛σi(t*)的表达可表示为
(4)
(5)
式中:τi=ηi/Ei为第i个Maxwell单元的应力松弛时间,min;σ0i为第i个Maxwell单元的初始松弛应力,N/ mm。
应力松弛前,历时t1加载至σmax且经过(t2-t1)后卸载至σ0时,第i个Maxwell单元的应力,即该单元的初始松弛应力σ0i可表示为[15]
(6)
图5所示模型的应力松弛方程σ(t*)可表示为
(7)
该应力松弛表达式可简化为
(8)
式中:A0=E0v(2t1-t2)/( 60L0) 。
(9)
式中:C0=A0-σ0。
上述模型由多个线性定参数弹簧和黏壶元件构建而成,同时,值得注意的是,在外加应力作用下,材料的微观结构将发生变化,材料某些力学参数将随时间的变化而发生变化,因而在构建元件模型时,需考虑元件参数的时间效应[29-30]。在构建非线性黏弹性元件建立变参数元件时,为便于计算,通常采用非线性黏滞体替代线性黏滞体,从而构建单变参数元件模型[4, 7, 9-11, 13, 30-34]。文献[35-36]在单变参数元件模型的基础上,基于元件的时间效应构建了双变参数Maxwell模型,并认为黏壶元件黏滞系数η(t)和弹簧元件弹性模量E(t)随时间变化的经验函数[35]可表示为
η(t)=η0t1-n
(10)
E(t)=E0tm
(11)
式中:E0为非线性弹簧的初始弹性模量,N/mm;η0为非线性黏壶的初始黏滞系数,N·min/mm;n和m均为常数,0
基于式(10)和(11),建立的双变参数广义Maxwell模型的本构方程可表示为
(12)
求解上述方程组,可得松弛过程中应力增量的表达式为
(13)
式中:Di为式(13)中微分方程进行不定积分求解时的常数项。
2.3 模型拟合分析
基于图4所示的应力变化量曲线,对上述两种模型拟合效果进行分析,拟合结果如图6和7所示。为避免过度定义未知参数而影响拟合效果,采用i=2广义Maxwell模型的应力松弛简化表达式对实测数据进行拟合分析。由于双变参数广义Maxwell模型的待定参数较多,故拟合参数初值需小心赋予,以避免出现拟合不收敛的现象。
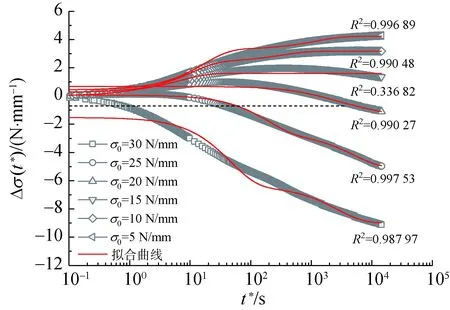
(a) 定常数广义Maxwell模型
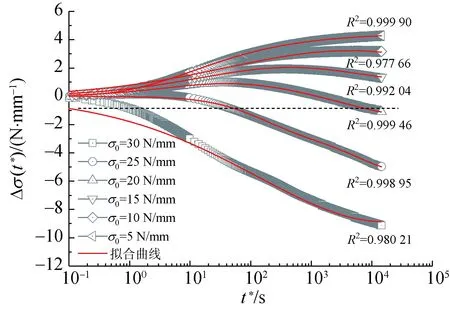
(b) 双变参数广义Maxwell模型

(a) 定常数广义Maxwell模型

(b) 双变参数广义Maxwell模型
由图6和图7可知,相比定常数广义Maxwell模型,双变参数广义Maxwell模型可较为准确地描述膜材松弛过程中应力变化量与松弛时间的变化情况,表明双变参数广义Maxwell模型适合拟合PVC膜材的简单应力松弛、混合应力松弛及逆应力松弛行为。
3 结 语
本文以PVC膜材为研究对象,对其松弛前历经应力回复后的应力松弛性能进行了测试与分析,并基于广义Maxwell模型建立了双变参数模型,试验与分析结果如下:
(1) PVC膜材的应力松弛行为与松弛前应力回复阶段的最大应力和初始松弛应力密切相关。当应力松弛前无应力回复时,材料表现典型的简单应力松弛行为;应力回复量较小时,表现为混合应力松弛行为;应力回复量较大时,表现逆应力松弛行为。
(2) 模型拟合结果表明,相比定参数广义Maxwell模型,双变参数广义Maxwell模型可较好地描述PVC膜材的简单应力松弛、混合应力松弛以及逆应力松弛行为。
(3) 因应力松弛前历经应力回复后的膜材对初始应力的保持能力较好,可调整现有膜结构表面预加张力的施加方法,减少膜结构表面张力损失,延长膜结构表面张力检测和调整的时间间隔,减少膜结构建筑的后期维护工作量。
影响膜材复杂力学性能的因素,不仅与组成成分的力学性能相关,还与增强织物的编织结构、织物与涂覆层界面性能密切相关,本文仅从大分子链的角度阐述了应力回复对应力松弛性能的影响,膜材内部组分材料结构的变化,特别是经纬纱线屈曲结构的改变和转化对应力回复条件下的应力松弛纤维的影响,还需做深入的研究。
因不同膜材组分材料的差异性和结构的多样性,不同膜材表现出不同的黏弹性力学性质,在预加张力确定的前提下,针对应力回复前最大载荷的优选,需要做进一步研究。
建筑膜结构用膜材的黏弹特性较为复杂,后续需对不同加载/卸载速度和温度下的长时间应力松弛行为进行研究。
