雷达导引头波形模糊函数仿真分析*

2020-12-02

舰船电子工程 2020年10期

（中国空空导弹研究院洛阳 471000）

1 引言

随着军事技术的发展，尤其是采用数字射频存储（Digital Radio Frequency Memory，DRFM）干扰产生技术的干扰机的广泛应用，空空导弹雷达导引头面临着越来越严峻的生存挑战。为适应日益复杂的战场环境，实现综合电子战条件下的精确打击，需要提高导引头的抗干扰能力。通过复杂波形优化设计进行抗干扰是导引技术发展的一个重要趋势。雷达波形设计与分析的一个重要工具是模糊函数，关于模糊函数的研究已经开展较多，并取得了一定的研究成果[1～3]。本文重点研究几种波形的模糊函数并分析其优缺点，进而指导雷达导引头的波形设计。

2 模糊函数理论

2.1 模糊函数的定义

模糊函数（Ambiguity Function）是波形设计及分析的重要工具，在分析导引头速度分辨率、距离分辨率、副瓣性能以及速度和距离模糊方面有着非常重要的作用，此外，它还可以用来分析距离-多普勒耦合。

其时域定义[4]如下：

对其进行傅里叶变换可以得到用信号频谱形式表示的等效定义：

模糊函数是两变量函数：其中变量t是相对于期望匹配滤波峰值输出的时延，变量FD是为滤波器设计的多普勒频移与实际接收的回波的多普勒频移之间的失配。

2.2 模糊函数的性质

模糊函数具有以下三种重要性质：

1）对原点的对称性

即表明雷达信号的模糊曲面对称于原点。

2）关于模糊函数的最大值，有如下特点：

即假设波形能量为E，当设计的滤波器对于距离和多普勒均匹配，滤波器相应输出最大值。如果滤波器不匹配，那么响应值将小于波形能量的最大值。

3）模糊体积的不变性，即

任何模糊函数曲线下的区域为恒值，这是一个十分重要的雷达信号定律，该能量守恒性质说明，在设计波形时，不能从模糊平面中移走一部分能量，而不将其补充到其他位置，而且它可以在模糊平面上任意移动。

3 几种常用波形模糊函数

3.1 线性调频波形（LFM）

线性调频波形是使用最多的脉冲压缩波形，它通过对载波频率进行调制以增加信号的发射带宽并在接收时实现脉冲压缩。其突出的优点是脉冲压缩系统对回波信号的多普勒频移不敏感，即使回波信号有较大的多普勒频移，脉冲压缩系统仍能起到压缩的作用。线性跳频信号的定义如下：

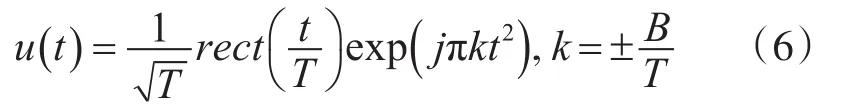
其中，T是脉冲宽度，B为带宽，根据模糊函数的定义计算，LFM波形的模糊函数为

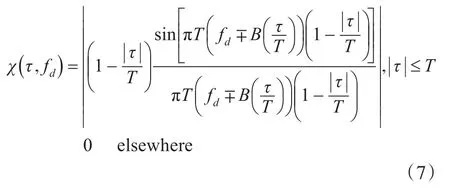
其中，T是脉冲宽度，B为带宽，τ为时延，fd为多普勒频移。

3.2 相位编码波形

与线性调频波形类似，相位编码也是通过信号的时域非线性调相达到扩展等效带宽的目的。将脉宽为T的导引头发射脉冲分解成N个脉宽为τ的子脉冲，并对这些子脉冲按载波相位进行编码。相位编码波形的定义如下：

其中，φ(t)为相位调制函数，对于二进制编码，φk=0，π 。可以用二进制序列{Ck=0，1} 表示，如果二相编码的包络函数为矩形函数，即

其中，N为码长，τ1为码元宽度。则可以将式（8）表示为

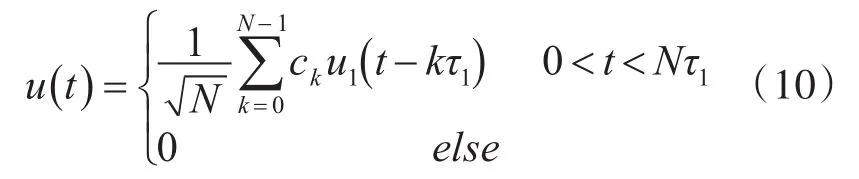
相位编码波形的模糊函数如下[5]

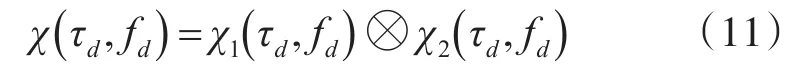
其中：

巴克码是一种二进制相位编码，其特性是编码的自相关函数的所有副瓣峰值幅度都等于1/N，N是编码长度。目前最大长度的巴克码N=13，即

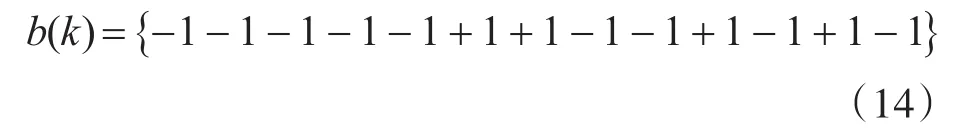
巴克码的优点是它们的副瓣包含的能量理论上可以最小且均匀分布，本文主要针对13位巴克码进行仿真分析。

3.3 Costas跳频编码波形

Costas跳频编码信号由J.P.Costas于1966年提出[6]，其与LFM的对比如图1所示，可以看出Costas编码的频率变化具有伪随机性，但是每个时间片和每个频率片都只有一个频率，因此，对于一个N*N的矩阵，可能的Costas编码的数目远远小于N！。

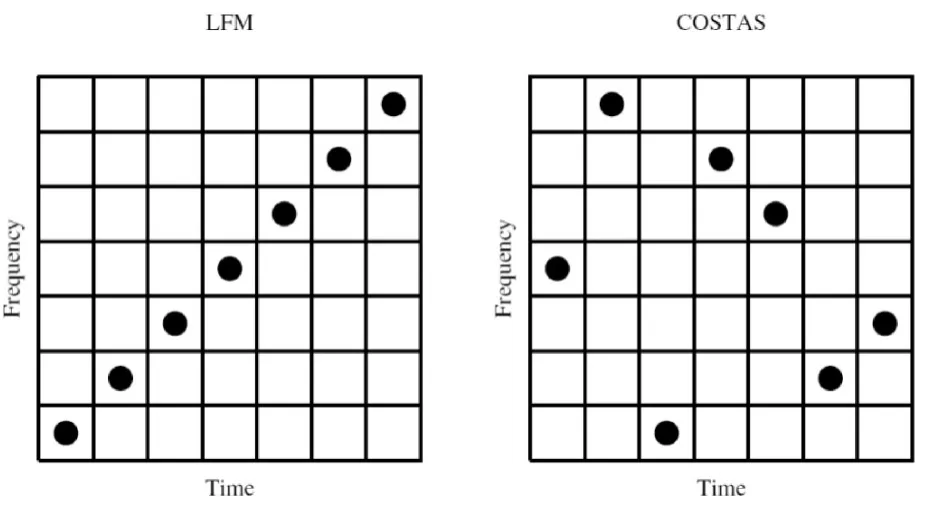
图1 LFM与Costas对比

Costas编码波形的模糊函数呈现图钉形状，副瓣低而平坦，具有良好的目标距离-多普勒分辨性能[7]，但其对速度非常敏感，当目标运动时，速度引入的附加相位会造成距离像多普勒失配，引起能量的发散，使距离像峰值产生严重失真[8]，因此速度测量和补偿成为这种信号实现后续目标检测的关键。Costas跳频编码波形的定义如下：

式中，T为脉冲宽度系数，Tr为脉冲重复周期，是为了分析方便，进行能量归一化，rect()为矩形窗函数，u(t)为阶跃函数，Cn表示N位Costas编码。

Costas编码波形的模糊函数如下：

令fd=0，τ=0，得到模糊的零多普勒表达式及零延迟表达式如式（17）～（18）。

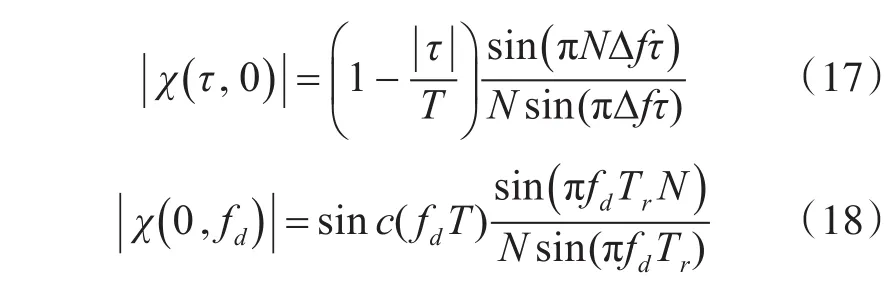
4 仿真分析

针对线性调频、巴克码、Costas编码三种波形进行仿真，对三种波形时域幅度进行归一化处理，巴克码采用13位巴克码，其编码见式（14），Costas编码采用7位Costas序列，其序列见表1，为方便对比，对模糊图的最大多普勒偏移、最大时延均进行归一化处理，其参数设置如表1所示。

按照参数设置，绘制的三种波形的幅度、相位、频率变化及模糊图见图2～4。

从图2可以看出，线性调频波形的模糊图形状为斜刀刃型，它同时具有大时宽带宽积和良好的距离分辨率，大的时宽保持雷达导引头的平均发射功率，进而提高其作用距离，提升其反隐身能力，良好的距离分辨力能够提高目标分辨能力，进而提高抗干扰能力。同时，线性调频波形对多普勒具有强稳健性，因此特别适用于空空导弹对于迎头攻击时目标的检测。

从图3可以看出，相位编码波形的模糊图近似为图钉型，距离与多普勒分辨力高，且其离散特性使得波形的产生特别灵活，可以用一组滤波器实现二进制编码波形以得到精确的距离和多普勒信息，但其对多普勒敏感，在使用时需要注意，并且目前巴克码最长为13位，限制了其可能的旁瓣抑制程度，空空导弹雷达导引头在实际作战中，经常面临低空下视，在地/海杂波较强时，低的旁瓣抑制会导致杂波从旁瓣进入，限制导引头的低空下视检测能力。

表1 仿真参数设置

图2 LFM信号的幅度、相位及频率变化及模糊图

图3 相位编码信号的幅度、相位、频率及模糊图

图4 Costas信号的幅度、相位、频率及模糊图

从图4可以看出，Costas编码波形的模糊图也近似为图钉型，同时具有高的距离与多普勒分辨率，但同时表明其具有多普勒的敏感的特性，在使用时要注意其多普勒容限，Costas编码波形因其具有随机跳频的性质，且可以结合脉内结合其他频率调制波形，脉间跳频使用，而干扰信号由于其滞后于发射信号，因而无法干扰到导引头，因此在抗干扰方面Costas编码波形具有较大的潜力，值得进一步研究。

目前，在空空导弹雷达导引头中，由于线性调频波形其产生简单，因而应用最为广泛，但是随着干扰越来越复杂，我们需要进一步提高距离分辨力与速度分辨力，进而提高抗干扰能力，但如果同时要求良好的距离分辨力及速度分辨力将导致信号处理机处理能力的增加，通常，对覆盖整个感兴趣的多普勒范围的多个模糊函数的每一个必须设计一个多普勒滤波器，而每个多普勒滤波器需要存储感兴趣的每个距离单元值，这大大增加了处理机的复杂程度，尤其是在空空导弹上处理机体积有限且散热受限，因而其处理能力有限，需要进行折中考虑。