改进模糊聚类分析在战术通信网络识别中的应用*

（国防科技大学电子对抗学院 合肥 230031）

1 引言

伴随网络中心战理念发展和技术进步，战术通信网络成为维系作战单元之间相互协同的核心要素，识别其组织结构将利于我方瘫痪敌作战体系进而夺取战场优势[1]。战术通信网络是由干线节点、入口节点以及通信传输系统构成的能够覆盖战术作战区域的栅格网络[2]，由于网络覆盖区域较广，组成要素相对复杂，加之战场复杂电磁环境，作战过程中往往难以对其组网结构进行有效识别。

目前国内大多文献主要集中于战术通信网络关键节点识别和对部分条件已知的无线传感器网络网络（WSN）组织结构发现研究上，较少有涉及战术通信网络识别的文献。其中文献[3]提出利用侦察获得的辐射源方位信息和时间接续特征识别通信专向和网络；文献[4]提出在辐射源信源位置聚类基础上通过判定节点类型和响应时间对战场干线拓扑进行推断；文献[5]应用目标编群理论逐层分析识别网络群簇划分；文献[6]提出用统计距离度量电台之间的位置关系并通过DBSCAN算法进行聚类，关联不同位置上的通信电台；文献[7]将通信电台与搭载雷达平台相关联，通过挖掘航迹和通联信息识别电台关系；文献[8]在密度峰值得到网台数目基础上利用成对约束条件和谱聚类分析识别网台。其中文献[1～2]主要从当前侦察手段出发定性描述战术通信网络识别过程；文献[3]重复遍历所有侦察信号信息的方法开销较大；文献[4]仅仅考虑了电台分布地址这一因素，识别可靠性较差；文献[5]平台关联和航迹挖掘方法在面对海量数据时计算复杂度较高，难以满足实际侦察需求；文献[6]应用谱聚类分析识别通信网台，体现出模糊聚类方法在网台识别中的应用价值。

社团发现算法是复杂网络研究的基础性问题，能够有效帮助理解网络的功能演化和组织结构，目前主要被划分为非重叠社团和重叠社团的发现算法[9]，较为典型的有Newmen提出的GN算法[10]、基于谱图理论基础的谱分析法、Raghavan提出的标号传播算法[12]（LPA算法）等。由于战术通信网络由其部队建制编成约束形成，其建制内的节点严格归属某一确定网络，故战术通信网络可视为一种非重叠网络。而由于战场侦察环境的复杂性使得侦察数据受限且识别结果具有动态不确定性，为此本文将战术通信网络类比为信息图，提出一种适用于战场环境的改进模糊聚类算法，通过寻找合适阈值得到战术通信网络最优划分，最后以实验仿真说明本文方法合理性。

2 理论基础

战术通信网包括路由/交换和用户终端等不同类型的节点，并由传输链路连接形成网络结构，本文应用信息图表示方法，将战术通信网络中的节点与边抽象出来构成图的表示。并介绍模糊聚类分析方法，为后文分析奠定理论基础。

2.1 基于信息图表示的战术通信网络

图是用来描述点以及点与点之间连接线所构成图形的数学工具，通常用G=(V，E)表示，其中V，E分别表示图中节点和边的集合，根据图中有无方向性区分为有向图和无向图。文献[13]提出描述网络内节点属性和连接关系的信息图概念，本文在此基础上进行拓展，应用信息图表示战术通信网络。假设某网络内包含n个节点，每个节点具有m个属性特征，以集合表述为X=(x1，x1，...，xm) ，xik表示为该节点第k个属性值，其权重表示为w(xk)；pij则表示为节点i和节点j之间构成的边，说明节点之间连接强度。具体表示为IG=(V，E，P，AS)，其中P，AS分别表示为战术通信网络中边属性向量和节点属性向量的集合，节点属性包括该通信节点的信号特征，如调制样式、信号载频、信号带宽等。边属性则表示节点之间关联疏密程度，如节点之间通信频次、通信流量等。

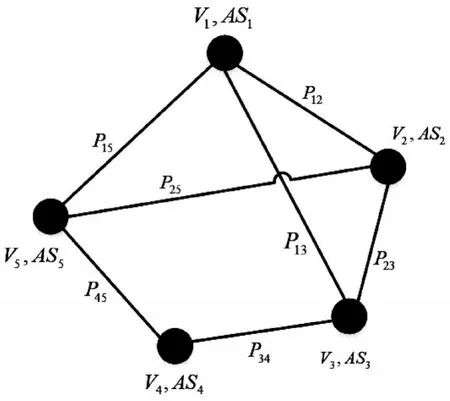
图1 战术通信网络的信息图表示

2.2 模糊聚类理论基础

模糊聚类分析是一种利用模糊数学知识处理对象分类的分析方法。传统基于经典集合论的聚类分析将每个辨识对象严格区分为不同类，属于硬分类方式，而基于模糊集合的聚类则适合应用于具有模糊属性的对象集合，是一种模糊动态分类的软聚类方法[14]。

2.2.1 基本概念

1）截矩阵与传递矩阵

设R∈μm×n，R=(rij) 对 于 ∀λ∈[0 ， 1]，记Rλ=(λrij) ，其中

则称Rλ=(λrij)为R的λ截矩阵。若R2⊆R，则R称作模糊传递矩阵，其中包含R且被任一包含R的传递矩阵称为R的传递闭包，记做t(R)。且对于任意R∈μm×n，总有

2）模糊相似矩阵与模糊等价矩阵

设R∈μm×n，若R满足传递性且满足自反性（I＜R）和对称性（RT=R），则称R为模糊等价矩阵。在有限域上的模糊等价关系确定后，对不同给定λ∈[0 ， 1]都有一个普通等价关系Rλ与之对应，λ从0到1变化时则形成动态分类。若R是自反且对称的模糊矩阵，则R称为模糊相似矩阵，其传递闭包t(R)=Rk必是模糊等价矩阵，可见模糊等价矩阵是模糊相似矩阵的特殊情况。

2.2.2 模糊聚类分析步骤

模糊聚类分析首先需对原始矩阵数据标准化处理，并在求取分类对象相似度基础上得到模糊相似矩阵，通过传递闭包得到模糊等价矩阵，遍历模糊等价矩阵内所有元素与阈值λ的大小后获得动态分类结果，最后确定最佳阈值获取分类最优解。

图2 模糊聚类分析步骤

3 基于改进模糊聚类分析战术通信网络识别

考虑到战术通信网络识别在实际作战环境中具有侦察不确定性，网络分界模糊，本文应用一种改进的模糊聚类分析方法识别战术通信网络，得到节点群簇划分。

3.1 模糊等价矩阵的建立

模糊等价矩阵的建立在于挖掘网络节点之间的相互关系。本文通过节点通信特征上表现出的相似/相异性或节点在通联关系上表现出的距离，将节点相互关系定义为节点关联度进行综合测算，测算公式表应用欧式距离：

ρ表示网络内两个节点关联度，xin表示第i个节点的第n个属性。标准化处理矩阵数据后，使其取值范围介于[0，1]区间内。

将给定战术通信网络作信息图表示：IG=(V，E，P，AS)，其中由RP构成网络边属性（通联关系）向量模糊相似矩阵，RS构成节点属性（信号特征）向量模糊相似矩阵[15]，分别记做：

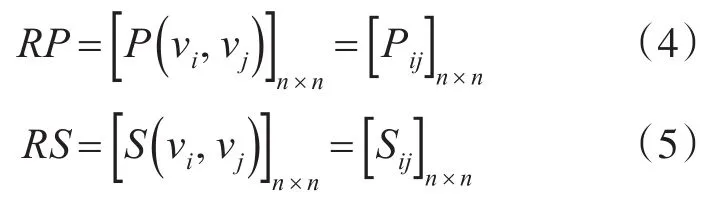
令δ1，δ2分别为边属性和节点属性权重，满足δ1+δ2=1。构造加权相似矩阵RV[16]如下：

此外考虑到战术通信网一般有着较为明确的地域划分，同一战术网络内的节点可归属于某一确定通信地域半径中[18]。本文以此作为模糊矩阵约束条件，构建修正模糊相似矩阵如下：

其中约束条件矩阵表示为

修正后的模糊相似矩阵表示为

修正后的模糊相似矩阵并不满足模糊等价矩阵传递性要求，为使得矩阵内部元素获得更加稳定的关系，需用传递闭包的方法将其转化为模糊等价矩阵。模糊等价矩阵建立过程可描述如下：

3.2 战术通信网络识别方法

选取不同阈值λ大小得到多个等价矩阵，构成动态网络分类效果。其中分类精度随着λ值的变化而改变：λ值越大分类越精细，λ值越小分类则越粗糙。当分类效果精细时说明划分网络内节点之间联系紧密，可能构成战术通信网内较低指挥层级的网络划分；相反，分类效果粗糙则说明网络节点联系疏松，可能构成较高指挥层级的网络划分。即在因侦察条件受限致使信号辨识模糊情况下，动态聚类效果有助于情报人员根据战场实际环境和需求灵活判断。整个识别步骤可表示如图3。

3.3 选取最佳阈值λ的讨论

模糊聚类分析中通常引入F统计量说明划分网络的差异性[17]，通过计算得到统计量最大值，确定节点差异程度最大时的网络划分。本文以此方法判断地域战术通信网络的最高层级网络划分结果。

假设模糊聚类分析过程中，对于设定聚类阈值λ存在r类网络划分。其中第j个网络中有nj个节点，通信节点集合表示为v=(v1j，v2j， ...，vnj) ，其特征向量表示为。设战术通信网中所有节点的中心向量为。则F统计量可表示为

其中式（10）分子部分表示划分网络之间的平均距离，分母部分表示网络内部节点间距。F统计量越大说明划分网络差异性越大且内部节点关联度越强，网络划分效果最优。

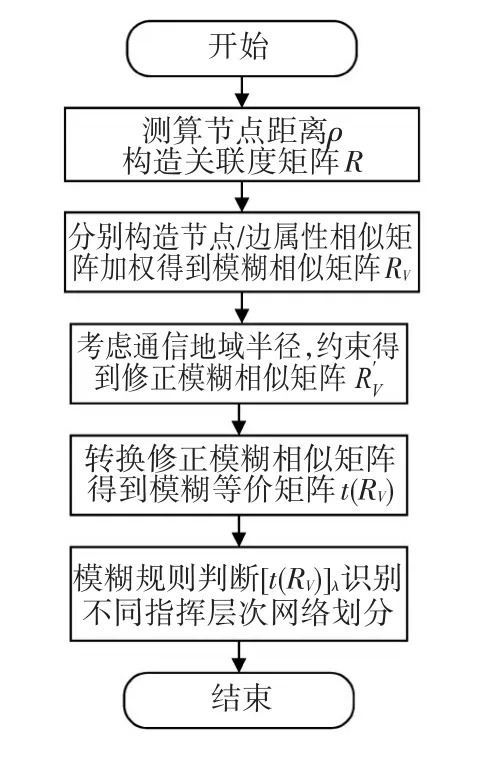
图3 战术通信网络识别步骤

4 仿真验证

为验证本文提出识别方法有效性，本文模拟某地域战术通信网络为背景，识别网络内节点的群簇划分。假设该地域战术通信网络包括有30个通信节点，侦察节点特征数据结构表示如表1。

表1 节点特征数据结构

现初步判明大致由四类网络构成。设通信节点集合表示为P=(p1，p2，...，p30)，属性集合表示为X=(x1，x2，x3，x4，x5)和Y=(y)，其中节点属性X表现为信号特征，依次为信号频率、调制样式、信号带宽、相对电平和频点个数；边属性Y表现为节点通信频次。

依据基于专家经验的AHP方法[18]确定节点属性权重划分（0.34，0.15，0.18，0.06，0.27），节点属性和边属性权重划分（0.65，0.35）。模拟节点/边特征参数如表2所示（调制样式转化为数值表示）。

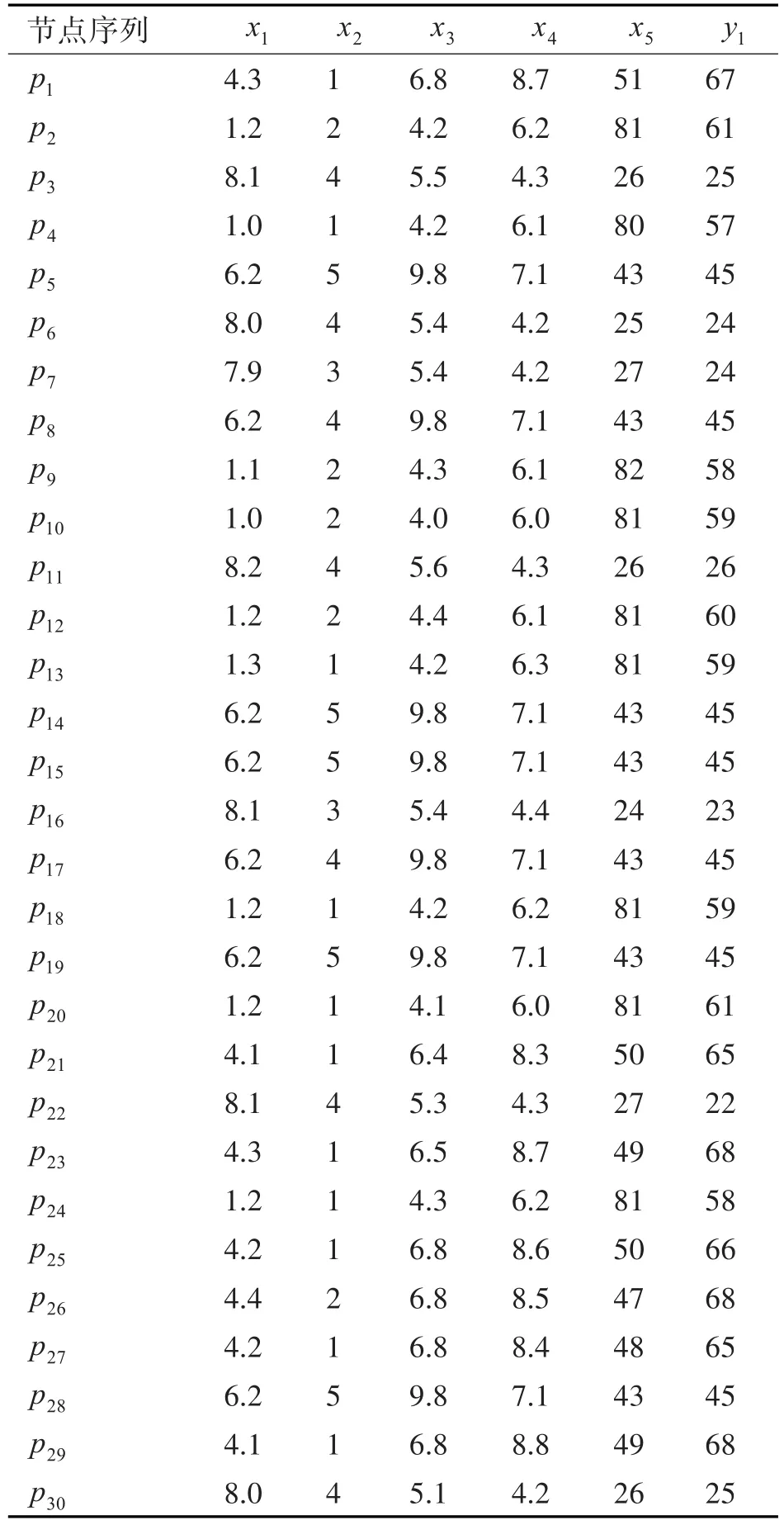
表2 战术通网络（节点/边）特征参数统计

以此构造节点属性和边属性模糊相似矩阵，经加权和修正后得到模糊等价矩阵，通过选取不同阈值λ大小获得动态聚类效果，计算不同分类数目下的阈值λ统计量大小。如图4～5所示。

图4 阈值分类数目对比

得到战术通信网络动态聚类效果如图6所示，同时结合图4可得，当F统计量为0.38时取得战术通 信 网 络 最 优 划 分 ：(p3，p6，p7，p11，p16，p22，p30) ，(p5，p8，p14，p15，p17，p19，p28) ，(p1，p21，p23，p25，p26，p27，p29)，(p2，p4，p9，p10，p12，p13，p18，p20，p24)。即网络类间和类内距离之比达到最大时可判定为战术通信网络高指挥层级划分，同时指出图中可能存在的高/中/低各指挥层级网络。

图5 阈值统计量大小对比

图6 战术通信网络划分

单独考虑节点属性，用Girman-Newman方法在聚类数目为4的条件下进行可视化分析[19]。同一划分用相同颜色进行表示。其划分类别分别为(p1，p5，p9，p13，p17，p21，p25，p29)(p2，p6，p10，p14，p18，p22，p26) (p3，p7，p11，p15，p19，p23，p27) (p4，p8，p12，p16，p20，p24，p28，p30)可见较多的节点被划分到错误的网络中，与实际结果存在较大出入。

图7 Girman-Newman聚类效果可视化

可见传统聚类方法由于需预先指定聚类数目在实际侦察环境中应用较为困难，相比而言本文改进模糊聚类方法能够在满足灵活性基础上将节点正确划分到所属网络中，提高了识别准确率。同时软性聚类方法更适用于复杂模糊环境下的动态识别，协助侦察情报人员根据作战实际情况判断不同指挥层次下的网络划分。

5 结语

对于侦察环境中存在的大量非协作通信信号，侦察过程中情报人员往往难以对战术通信网络区分识别，本文将战术通信网络类比为包含节点与边的信息图表示，应用改进模糊聚类分析方法，识别战术通信网络节点的群簇划分。实验结果表明，相对于传统聚类方法，经过修正的模糊聚类分析方法不但优化了识别准确率，同时还具备对战术通信网络的模糊区分效果，能够协助作战人员根据战场实际情况判断不同指挥层次下的网络划分，与传统聚类分析需要预先制定聚类数目的要求相比，更加具有灵活性。