基于AFSA-SVM的船体外板变形预测
2020-12-01董梁何祖军齐亮葛成威
董梁 何祖军 齐亮 葛成威

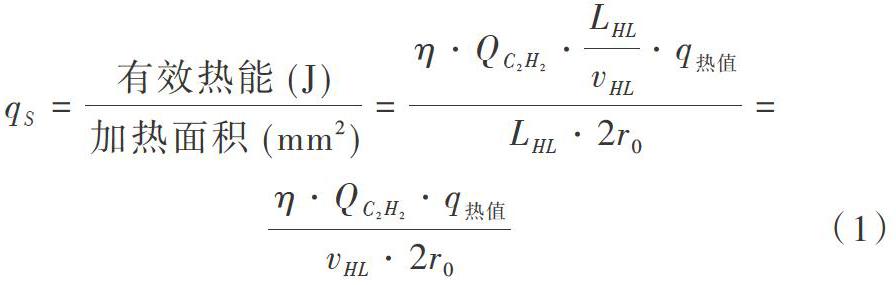
摘 要:船体外板复杂曲面自动化加工一直是船舶制造业研究热点和难点,由于加工过程中船板变形影响因素过多,导致船板加工变形预测一直不够准确快速。鉴于此,将两种复合变量用来表征加工过程中热源对应的众多加工参数,采用人工鱼群算法(AFSA)优化的支持向量机(SVM)预测船板变形。经实验验证,复合参数输入的AFSA-SVM模型预测船体外板水火线加热工艺变形线平均精确度为99.87%,角变形平均精确度为99.53%,且全局最优。将其与传统的PSO-SVM模型对比,不仅精确度有了提高,而且避免了局部极值导致的部分预测结果误差过大情况。
关键词:人工鱼群算法;支持向量机;船体外板;有限元仿真
DOI:10. 11907/rjdk. 201264
中图分类号:TP319文献标识码:A 文章编号:1672-7800(2020)010-0129-04
Abstract: The automatic machining for the complex surface of hull plate has always been a hot spot and difficult point in the shipbuilding industry. Due to the various factors affecting the deformation process for the ship plate in processing, the deformation prediction of the ship plate has not been accurate and fast enough. In view of this, the two composite variables are used to characterize many processing parameters corresponding to the heat source in the processing process, and the support vector machine (SVM) optimized by artificial fish swarm algorithm (AFSA) is used to predict the deformation of the ship plate. Experimental results show that the average accuracy of linear deformation and angular deformation for the AFSA-SVM model based on the composite parameters input are 99.87% and 99.53% respectively, and it is global optimization. By comparing it with the traditional PSO-SVM model, we find that not only the accuracy is improved, but also the large partial prediction error caused by local extremum is avoided.
Key Words: AFSA; SVM; ships hull plates; FEA
0 引言
水火弯板工艺一直是船体外板曲面成形的主要工艺,因操作灵活、设备简单、成本相对低廉等特点被船厂广泛采用[1]。但目前这项工艺依托工人手工操作,加工过程中的主要参数都依托工人的经验判断。为推动船体外板曲面成形工序的自动化,船板变形量与加工参数关系成为研究重点。传统的研究方法是使用有限元建模仿真(Finite Element Analysis,FEA)计算船板变形,通常使用ANSYS软件,但这种方法计算量过大、耗时长,难以普及。随着神经网络、人工智能技术发展,智能算法受到青睐[2]。
冯志强[3]采用粗糙集建模方法,对船板变形进行近似推理;段珏媛[4]尝试使用支持向量机(Support Vector Machine, SVM)对船板变形进行预测;陈尤力[5]使用粒子群优化算法(Particle Swarm Optimization Algorithms,PSO)优化支持向量机,提高预测准确性;王宇哲[6]采用SVM和BP神經网络,选用不同加工参数进行组合,研究各加工参数对船板变形的影响。
在众多神经网络模型中,支持向量机(Support Vector Machine, SVM)面对非线性、高纬度、小样本问题时表现较好[7],本文使用SVM对船体外板加工变形进行预测。针对SVM存在的模型参数确定问题,使用人工鱼群优化算法(Artificial Fish School Algorithm, AFSA)对SVM模型进行参数优化。同时,使用板厚和两种复合变量作为预测模型中的输入,以船板的线变形和角变形作为输出,减少复杂且众多的加工参数输入,以简化模型,提高运算精度。
1 水火弯板变形机理
在水火弯板线加热工艺中,钢板温度场主要受表面承受的加热热源影响,这股热量不均匀施加在钢板上,导致钢板温度场分布不均匀,进而使钢板内部膨胀不均匀。受到加热的部位迅速膨胀,未加热部位有约束,在残余应力作用下导致钢板变形。因此,输入热源对钢板变形量影响很大。热源参数如图1所示。
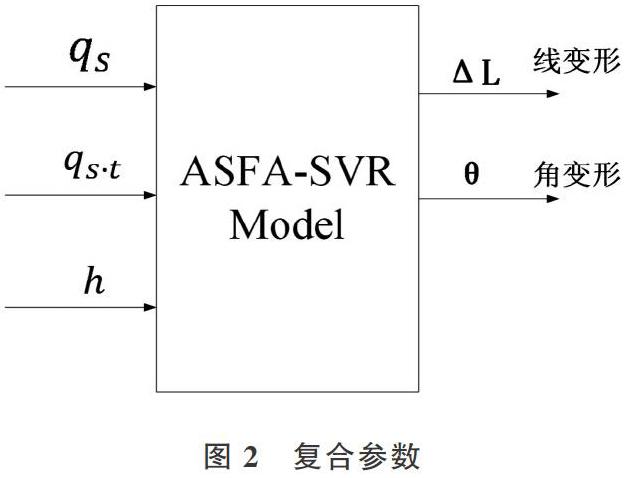
针对图1输入热源因素,参考文献[3]将这些影响因素整合为板厚与两个表达热源输入的复合变量[qs]和[qs·t],如图2所示。
其中,变量[qs]代表单位面积下加热热源输入的有效热量,表征[QC2H2](乙炔流量)、[vHL](加热速度)、[η](热源效率)、[r0](热源半径)等参数;[qs·t]代指单位时间下加热热源输入的有效热量。这两个复合参数数学模型如下:
使用两个复合参数后,没有了原本众多的输入参数,极大简化了预测模型,减少实际运算量。这两个复合参数又很好地表达了热源对钢板的影响,提高了运算准确度。
2 支持向量机
支持向量机起源于20世纪90年代,至今已成为机器学习技术中解决非线性、小样本和高纬度问题最实用的方法之一[8]。
SVR算法原理:
式(3)中,[Φ(x)]为非线性映射函数,其主要作用是把数据映射到高维特征空间内,b定义为偏置,w定义为权向量。
支持向量机核函数有linear(线性核函数)、PKF(多项式核函数)、RBF(高斯径向基核函数)3种,其中RBF应用最为广泛,能适应任何维数容量样本,且收敛域较宽[9],故本文选择RBF核函数。对于支持向量机,其参数优化的实质就是选择核参数r和惩罚因子C。如果C值过小,模型会欠学习,导致经验风险较大;如果C值过大,模型过学习,会引起同样的风险,r取值与C一样。下面使用人工鱼群算法对核参数和惩罚因子进行优化,得出最优参数,提高模型预测精度。
3 人工鱼群算法
人工鱼群算法是基于动物社会性活动特征原理的群体智能优化算法,通过模仿鱼类觅食行为在指定搜索区域空间内寻优。人工鱼群算法拥有很强的寻优能力且不易陷入局部极值,对初值不敏感,鲁棒性强[10]。
3.1 人工鱼群算法定义
有N条人工鱼组成一个鱼群,设其中一条鱼的状态为[Xi=xl,l=1,2,…,n]。人工鱼的食物浓度用作目标函数的适应度值,单个鱼状态作为优化变量,适应度值可由优化变量获得,即:[Yi=f(Xi)]。人工鱼[Xi]与[Xj]距离为[dij=Xi-Xj]。 拥挤度因子为[δ],它表示附近的拥挤程度。人工鱼可以感觉到的范围是Visual,根据其它鱼在感知范围内的行为确定运动方向。人造鱼步长为Step,饲养过程次数为Try-number。
人工鱼群算法通过觅食、聚群和追尾3种仿生行为模式实现。
3.1.1 觅食行为
以第i条人工鱼为例,当前位置为[Xi],在其视野范围[(dij 3.1.2 聚群行为 同样以第i条人工鱼为例,当前位置为[Xi],当前i的视野范围内有nf条人工鱼。任意两条人工鱼i,j距离为[dij=Xi-Xj],其食物浓度为[Yi]。将视野范围内人工魚的状态和[Xs]除以条数nf,得到邻域中心状态[Xc]。[δ]为拥挤度因子,若此时[Yc/nf/δYi],则表示领域中心并不拥挤,向其移动一步,公式如下: 3.1.3 追尾行为 以第i条人工鱼为例,当前视野范围内[(dij 3.2 AFSA-SVM算法实现 人工鱼群算法实现步骤:①初始化设置,包括种群规模N、每条人工鱼初始位置、人工鱼视野Visual、步长Step、拥挤度因子[δ]、重复次数Try-number;②计算初始鱼群适应值,取最优人工鱼状态将其值赋予公告板;③对每个个体进行评价,选择执行行为,包括觅食Pray、聚群Swarm、追尾Follow和评价bulletin;④执行人工鱼行为,更新后生成新鱼群;⑤评价所有个体,若某个体优于公告板,则将公告板更新为该个体,否则公告板数据不变;⑥当公告板上的最优解在误差界内或达到算法迭代次数上限时,算法结束,否则转步骤③。 4 实例分析 为验证AFSA-SVM预测模型的有效性,本文通过 Ansys 软件进行有限元仿真,并结合实际加工得到的若干组数据,收集一批船舶通用材质低碳钢钢板在不同流量、速度下的变形数据。钢板物理参数与文献[7]相同,选用长宽1000mm×1000mm,厚度分别为12mm、14mm、16mm的钢板进行仿真。每种厚度随机选取30组数据作为训练样本,每种厚度选3组数据作为仿真测试样本。 4.1 AFSA-SVM预测模型 AFSA-SVM预测模型算法步骤如下:①首先筛选数据,建立训练样本和测试样本,对训练样本归一化处理,提高模型运算速度;②初始化各项参数;③以支持向量机回归结果的平均方均根误差倒数为适应度,采用人工鱼群算法步骤优化SVM模型参数。设人工鱼群个数[N=150],单个鱼视野Visual=10m,移动步长Step=20m3,拥挤度因子[δ]=0.618,最大试探次数Try-number=10;④利用人工鱼群算法得出最优参数,建立最优的SVM模型,对训练数据展开训练;⑤训练完毕后将预测结果与测试样本进行对比。 4.2 预测结果分析 仿真结果如图3、图4所示。图中圆圈表示实际线变量和角变量值,三角形表示利用AFSA-SVM模型得到的预测值,可以看出钢板线变形和角变形仿真值与预测值基本一致。分析数据后,得出线变形平均精确度为99.87%,角变形平均精确度为99.53%,二者的变形量预测都取得良好的拟合效果。 为更进一步验证AFSA-SVM预测模型可行性与精确度,对上述90组训练样本采用传统的PSO-SVM建模,并将测试结果对比,用误差百分比评鉴预测精度,见表1。从表 1 可以看出,AFSA-SVM 模型的整体预测精度明显优于传统的PSO-SVM预测精度。 由表1计算出AFSA-SVM模型线变形和角变形的平均误差为0.13%和0.47%,PSO-SVM模型线变形和角变形平均误差为0.38%和0.70%。经过人工鱼群算法优化,线变形和角变形预测结果误差减小幅度为65%和32%。可以看出,AFSA-SVM模型达到全局最优,PSO-SVM模型部分结果出现误差较大及局部极值情况。 5 结语 本文采用AFSA优化SVM的回归预测模型预测船体外板水火线加热工艺的变形量,利用板厚与表征热源对应的众多加工参数复合变量预测钢板变形量。使用人工鱼群算法避免了传统PSO-SVM模型易出现局部极值导致部分结果误差较大的情况;使用复合变量提高了模型运算速度与精度。实验结果表明,AFSA-SVM预测模型对实际船体外板曲面成形加工有一定的指导意义,可应用在实际生产中。 参考文献: [1] 张成龙. 水火弯板变形机理关键参数研究[D]. 镇江:江苏大学,2014. [2] QI L, YU F. Research on expert system for line heating[C]. Tokyo:International Conference on Frontier Computing,2016. [3] FENG Z Q,YANG R Q, LIU C G, et al. Modeling based on fuzzy rough set with application to prediction of line-heating deformation[J]. Ship Engineering, 2016,45(12):41-45. [4] 段珏媛,叶树霞,齐亮. 基于LSSVM的水火弯板变形预测方法[J]. 自动化与仪器仪表,2015,14(1):142-144. [5] 李彦,陈尤力,齐亮. 基于PSO_SVM模型的水火弯板变形预测研究[J]. 舰船科学技术,2015,37(7):54-57. [6] 王哲宇,柳存根,杨志. 基于数据挖掘的水火弯板变形预测[J]. 热加工工艺,2019,48(1):129-133. [7] 丁世飞,齐丙娟,谭红艳. 支持向量机理论与算法研究综述[J]. 电子科技大学学报,2011,40(1):2-10. [8] 孙德山. 支持向量机分类与回归方法研究[D]. 长沙:中南大学,2004. [9] 王丽婕,厉虹,方市彬. 基于人工鱼群优化算法的支持向量机短期风电功率预测模型[J]. 电气工程学报,2016,11(10):7-12. [10] 李素,袁志高,王聪,等. 群智能算法优化支持向量机参数综述[J]. 智能系统学报,2018,13(1):70-84. [11] 齐 亮,杨 平,张成龙. 水火弯板成形因素对钢板表面温度和变形的影响[J]. 船舶工程,2013,24(6):87-90,111. [12] DENG Y P, GUO P J, LIU Y J, et al. Design and implementation of technological parameter prediction system for hull plate formed by line heating[J]. Ship Engineering, 2008, 30(1): 61-65. [13] 齐亮. 船体外板曲面线加热成形关键技术研究[D]. 镇江:江苏大学,2016. [14] FENG Z Q, YANG R D, LIU C G, et al. Modeling based on fuzzy rough set with application to prediction of line-heating deformation[J]. Ship Engineering, 2016,45(12):41-45. [15] QI L, LI T B. Research on ship-hull plates curve forming by means of line heating with variable velocity[J]. International Journal of Materials and Structural Integrity, 2016, 10(1/2/3):99-107. [16] 罗娜. 数据挖掘中的新方法——支持向量机[J]. 软件导刊,2008,7(10):30-31. [17] 李世文,李立聪. 自适应OSTU算法在舰船边缘检测中的应用及其FPGA实现[J]. 软件导刊,2019,18(6):176-180. [18] 趙晟然,伍常亮. 基于SVM的智能统分自学习系统设计与实现[J]. 软件导刊,2019,18(8):127-130,135. [19] 赵妍,乐燕芬,施伟斌. 基于微粒群优化LSSVM的室内指纹定位算法[J]. 软件导刊,2019,18(4):87-90,94. [20] 孔梦君,于莲芝,吴志强. 基于IWO-PSO优化支持向量机的模拟电路故障诊断[J]. 软件导刊,2019,18(5):53-57. [21] 余胜威. MATLAB 优化算法案例分析与应用 [M]. 北京:清华大学出版社,2014. (责任编辑:杜能钢)
