基于MATLAB的电磁振动仿真分析
2020-12-01余家敏吴建民
余家敏 吴建民

摘 要:针对振动摩擦焊接机在焊接过程中的外激振力幅值确定较为困难的问题,对振动摩擦焊接机中的电磁振动原理、电磁力计算、电磁力仿真分析等方面进行研究,对静态进程模式下正余弦信号与电磁力之间关系进行归纳,提出一种基于MATLAB的电磁振动仿真分析方法。结合电磁振动学和牛顿运动学方法综合建立简化的电磁力理论推导,借用MATLAB分析正弦和余弦对电磁力的影响规律,利用振动摩擦焊接试验台对所建立的电磁力理论推导方法进行实验验证。研究结果表明,当输入正弦信号,时间为0.002 5s时,电磁力最大值为400N;当输入余弦信号,时间为0.002 6s时,电磁力最大值为556.080 0N,从而为振动摩擦焊接机的外激振力及其频率确定提供了依据。
关键词:电磁振动;摩擦焊接;电磁力;MATLAB
DOI:10. 11907/rjdk. 201272
中图分类号:TP301文献标识码:A 文章编号:1672-7800(2020)010-0116-05
Abstract:Aiming at the problem of setting the external exciting force range of vibration friction welding machine in the welding process, we conduct research on the basic principle, the electromagnetic force calculation and the electromagnetic force simulation analysis in vibration friction welding machine. The relationship between the sine and cosine signal and the electromagnetic force is summarized in static process mode, and a simulation analysis of electromagnetic vibration based on MATLAB is proposed. Combined with the method of electromagnetic vibration and Newton kinematics, the simplified theoretical derivation of electromagnetic force is established, and the influence of sine and cosine on electromagnetic force is analyzed by MATLAB. The theoretical derivation of electromagnetic force is tested by using the vibration friction welding test bench. The results indicate that when sinusoidal signal is input and the time is 0.002 5s, the maximum value of electromagnetic force is 400N; when cosine signal is input and the time is 0.002 6s, the maximum value of electromagnetic force is 556.080 0N, which provides a basis for the external exciting force and frequency of the vibration friction welding machine.
Key Words: electromagnetic vibration; friction welding; electromagnetic force; MATLAB
0 引言
振動摩擦焊接是一种基于电磁传动机构的绿色制造技术,通过推动升降台发生相对动作,从而产生摩擦热,当实际温度达到临界温度时,塑性零件开始融化升温,完成焊接[1]。在振动摩擦焊接过程中,施加的电磁力会影响焊接质量和精度[2]。由于确定振动摩擦焊接设备在焊接过程中的电磁力幅值较为困难,很多学者纷纷对电磁力计算分布进行了研究。如刘勇等[3]依据叠片设计原理,利用数值模拟计算方法分析电枢结构的电磁力分布,可为电枢机构优化设计提供参考,但模型构建较为复杂,且耗时长;王玉彬等[4]以静密封高温超导磁通切换电机为例,利用三维有限元分析方法和麦克斯韦方程,对高温超导线材所承受的电磁力进行理论推导,得到电磁力仿真结果,但理论计算值结果波动较大;邓清鹏等[5]利用电磁力到结构网格的映射算法对电磁力及噪声进行快速仿真,并对电磁力分布稳定性进行分析;栾世奕等[6]依据等效磁路原理,采用Ansoft对电磁力进行数学建模,得到电磁力变化和分布规律仿真结果,经过实验验证,基本符合理论模型仿真的电磁力响应曲线结果。
本文针对上述研究存在的不足,提出基于MATLAB的电磁振动仿真分析方法,并在静态进程模式的单线程与多线程导电输入情况下分别对电磁振动进行分析。
1 电磁振动基本原理
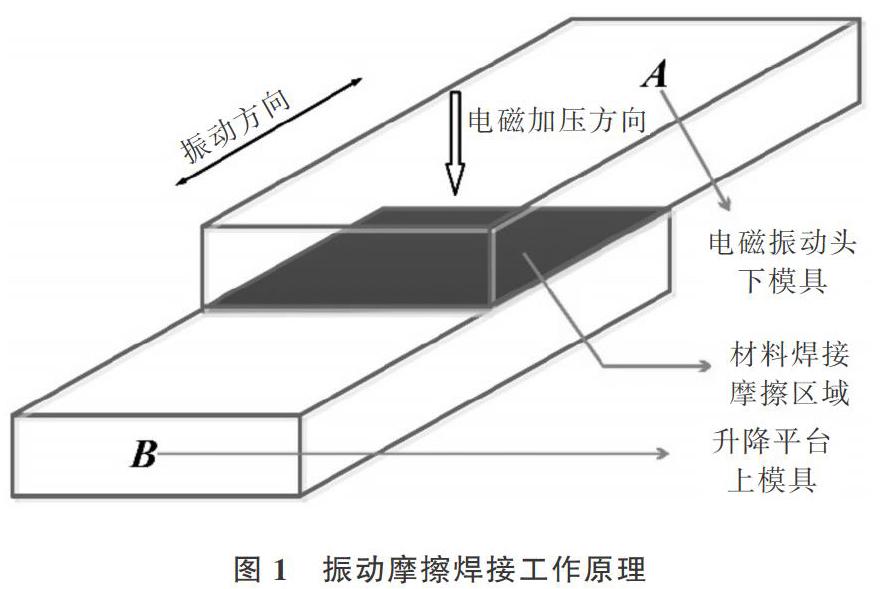
振动摩擦焊接技术是基于摩擦焊接原理,先把零件夹紧在电磁振动头与升降台之间,通过调节电磁振动头频率使其中一种材料跟着振动头做振动动作,另外一种材料按照设定的振动方向来回移动摩擦生成焦耳热量,并产生一个对地的轨迹参考距离[7]。同一水平位置点之间的距离称为振幅,一定时间内振动的平均次数为100或240,相对运动之间的表面痕迹所囊括的区域称为焊接区域[8]。一般将被振动材料加装在升降台固定模具上,其它材料按照装配位置被加装在电磁振动头上。升降台沿着垂直于电磁振动头的方向进行升降动作,液压泵控制压力并为其提供升降动作动力,如图1所示。
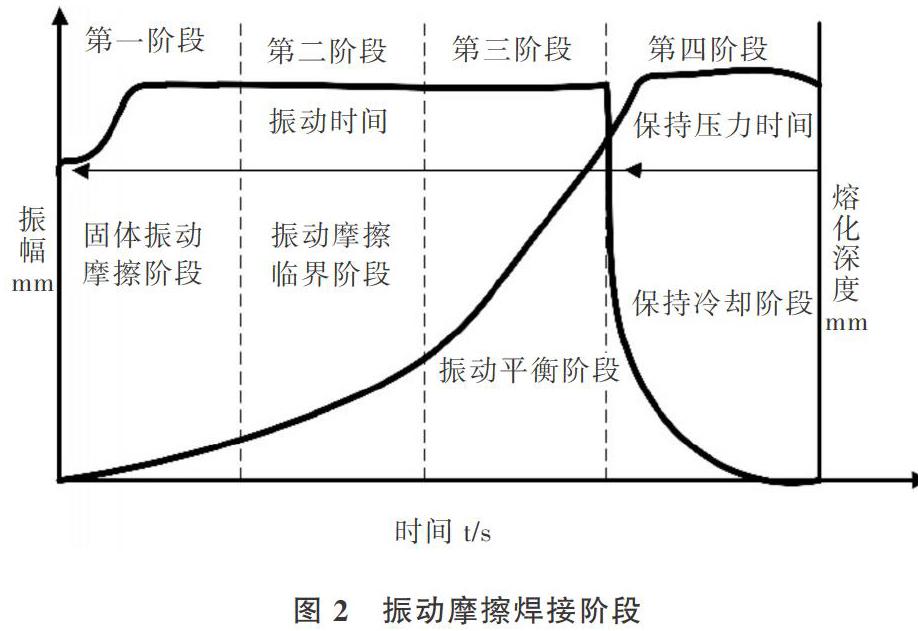
两种材料必须利用升降台的夹紧力,通过电磁振动头振动而相互焊接在一起。在振动时间和保持压力的时间周期内,有一持续不断的力群作用在塑性材料表面。在交流电压作用下,振动头频率达到共振临界条件而振动,经过一段时间,塑焊件就会被熔化。相对运动所花的时间称为“动摩擦焊接时间”,简称“焊接时间”。熔化的塑料在压力下短时间被冷却下来并固化,该时间被称为“保持压力时间”,简称“保压时间”,“保压时间”结束后,升降台下降并回到原位。振动摩擦焊接具体可分为固体振动摩擦阶段、振动摩擦临界阶段、振动平衡阶段和保持冷却阶段[9],如图2所示。
2 电磁振动理论分析
2.1 常规电磁力理论分析
本課题所用的振动摩擦焊接的核心部件之一是电磁振动头。通过对电磁振动头施加一定频率和压力,促使电磁振动头本身沿着振动方向进行往复振动,通过摩擦生热焊接,而推动电磁振动头往复振动的动力来源于电磁力。往复振动的定义就是某一部件在位置上的变化现象,这种变化现象包括位置规律变化和方向规律变化[10]。当部件在初始位移为0的位置开始变化时,方向规律有2个,向振动的正方向规律变化称为正方向规律变化,来回向前振动的位移称为正行程位移;向振动的反方向规律变化称为负方向规律变化,来回向后振动的位移称为负行程位移。振动的变化规律区域划分原理与笛卡尔坐标划分原理相似,从原点0开始进行分割,分为正向振动区域、负向振动区域和原点临界区域3部分。振动路径为:从初始位移为0的位置振动到正行程位移位置,从正行程位移位置振动到初始位移为0的位置,从初始位移为0的位置振动到负行程位移位置,从负行程位移位置振动到初始位移为0的位置,反反复复、来来回回振动。根据物理学、电磁学和机械振动学相关理论,本文研究的电磁振动头产生电磁力的装置模型可简化为电磁机构模型,这种电磁机构模型主要通过输入交流电,在电磁机构周围区域形成电磁场,从而产生电磁振动头振动所需的电磁力。
根据铁磁物质的电流与磁场回路原理,假设在输入交流电的电磁机构或装置附近区域产生了电磁场,在该电磁场中存在某一个交流电回路或线路回流[11]。在电磁场中施加给线圈、媒介或导电材料的电磁力为[FC],理论上电磁力产生了一个假想的电磁位移[SC]。根据物体做功过程其实就是能量相互转换过程的定义可得,电磁场机械所做的功[Wmc]与电磁力[FC]及电磁位移[SC]关系如下[12]:
公式(1)是宏观物理学做功计算公式,对于电磁场产生的电磁力而言,假设使用上述公式计算,比较复杂且不好量化,因此需要对公式(1)进行适当修正与变换。根据微积分原理,现取电磁位移Sc上一段假想可微分的电磁位移[dSC],则对应的可微分电磁力机械做功公式为:
将公式(2)进行微积分变换后得到变形式:
公式(4)中,由于电磁场输入的电流为交流电,而交流电电流和电压大小及方向每时每刻均在变化,导致从交流电输入开始,经过导电材料施加在电磁机构装置上的电磁力每时每刻均在变化,因而电磁场的电磁力能量[WEC]也同步发生变化。每产生一个可微分的电磁力[dFC],就会生成一个电磁微分能量[dWEC]。同时,电阻、导线等会因为电流经过而发热,从而损失一部分能量,电源输入带来的能源供给比理论能量值低。如果除去因发热损失的能量,则电磁场链路的能量变化量约等于电磁场电磁力能量[WEC]的变化量加上电磁场电磁力所做的机械功[Wmc]。
此外,电磁场产生的电磁力Fc是看不见、摸不着,但又真实存在的,位移Sc是为了问题求解方便、模型建立便捷而假设的。因此,取的假想位移Sc形式不同,电磁力计算公式可能不同,但最终结果分析是相同的,不影响对问题的分析及电磁力计算[13],如公式(4)可得如下变形式:
公式(5)、(6)中,[BZC]为在电磁场单位面积磁感应分布密度,[nZC0]为电磁场单位面积法向量,[μZC]为真空磁介质中磁感应分布密度与磁场分布密度的微分比例。
2.2 静态进程模式电磁力理论分析
静态进程模式由单线程导电输入与多线程导电输入组成。在单线程导电输入下,为了使电磁振动系统稳定性强,从物理的角度分析,电磁振动理想结构模型主要分为三相模型结构和四相模型结构[14],本文采用三相模型结构对静态电磁力进行计算与分析,其模型可简化为平面“E”型电磁机构装置,如图3所示。
在图3中,以中心虚线为分割线,左右两个结构为对象,显然左右两个电磁机构是根据中心虚线完全中心对称,则电磁机构模型的电流、面积、气隙磁导、电阻等物理参数均是对称的。不妨假设中心虚线左边方向的磁路有效面积为[SLC]、气隙磁导为[ΛC]、有效电阻为[RC]、有效电流为[iC1],那么根据电磁模型结构的对称性可得到中心虚线左边方向的磁路面积为[SLC=SRC]、气隙磁导为[ΛCS]、有效电阻为[RCS]、有效电流为[iC1=iC2],以中心虚线为基准的中间磁路有效面积[SΦCC=SRC2]。电磁机构单线程导电电流经过通电线圈,集中绕组铁芯材料上产生的磁通势能为[Ni],这种磁通势能与物理学上的机械势能、重力势能、电动势能等原理相似。以中心虚线左边方向磁路作为分析点,由物理学定律可推导得到[Ni]计算公式为:
由公式(7)可计算得到磁感应强度[BZC]为:
由于左侧方向磁路的电路是中心对称的,根据安培右手法则可知,假设磁通量是由外到内,并垂直于平面时,电流经过两根导线的电磁力大小一样,方向相同。于是由公式(6)、(8)可得左侧部分电磁力为:
同理,可得右侧部分电磁力为:
公式(9)、(10)中,[FLC]为左侧磁路部分电磁力,[FRC]为右侧磁路部分电磁力,[SLC]为中心虚线左边方向的磁路有效面积,[SRC]为中心虚线右边方向的磁路有效面积。根据物理学的力学合成方法,可得到“E”型对称的模型结构受到的电磁力为:
由公式(10)可知,通电线圈在结构模型、绕组数N和气隙C保持固定不变的情况下,电磁振动系统所受电磁力[FC]与电流大小有关。假如通电线圈输入大小和方向均不改变的电流时,电磁力[FC]为一个恒定数值,即大小和方向从初始状态到振动状态始终保持相同。
在实际应用中,电磁振动头要能根据生产要求实时调解焊接力度和频率,因而电磁振动头常将大小和方向均进行周期性变化的交流电作为电磁振动系统的输入。假设给图3所示的单线程导电三相电磁模型结构输入交流电,交流电电流为[i],电压为[u],1s内交流电方向和大小变化次数为[f]。为降低问题求解的复杂度,将图3模型简化成一个闭合电路模型,如图4所示。
在图4中,根据气隙磁导在并联电路中电流的合流规律,左边的气隙磁导[ΛCS]与右边的气隙磁导[ΛCS]是并联关系,然后左右两边并联后与中间的气隙磁导[ΛCC]串联。同理,左边电阻[RCS]与右边电阻[RCS]是并联关系,然后左右两边并联后与中间电阻[RCC]串联[15];左边电流[iC1]与右边电流[iC2]也是并联关系,然后左右两边并联后与中间电流[iCC]串联,其中[Ni]可参考电源电动势能。于是可得到整个电路的气隙磁导[ΛC]、电阻[RC]、电流[iC]计算公式为:
将公式(13)进一步简化得到气隙磁导计算公式为:
假设电磁振动头输入的交流电电流为[i=IM?cos2πft],电压为[u=UM?cos2πft],归算漏磁磁导为[Λgs],则根据公式(11)可得电磁力[FC]与交流电电流[i]及电压[u]的关系:
3 电磁力仿真结果分析
當在静态进程模式下进行单线程导电输入时,利用编程软件MATLAB对电磁力分布规律进行仿真,如图5、图6所示。
当在静态进程模式下进行多线程导电输入时,利用编程软件MATLAB对电磁力分布规律进行仿真,如图7所示。
在图5、图6中,在正弦和余弦交流电信号下,电磁力大小同步增加,方向刚好相反。当交流电按照正弦规律变化时,电磁力[FC]曲线走势在0~0.005s内先上升后下降,当时间为0.002 5s时,电磁力[FC]最大值为400N,之后进行周期性变化;当交流电按照余弦规律变化时,电磁力[FC]曲线走势在0~0.005s内先下降后上升,当时间为0.002 6s时,电磁力[FC]最大值为556.080 0N,之后进行周期性变化,这也从侧面验证了要使电磁振动头实现往复振动以达到焊接目的,必须给电磁振动系统输入交流电。同时验证了可通过调节电源频率以调节外激振力频率[f],且电源频率与振动频率的比例为50%,振动摩擦焊接机的外激振力[FN]可参考已求解的电磁力[FC]。
在图7中,静态电磁力幅值为[3FCP],方向角、方向角速度以及电子转速始终与输入系统的自然频率或电源频率呈正相关,且大小分别为[4πf]、[4πfrad/s]、[2f(r/s)],可为振动摩擦焊接处在空运行(未焊接材料状态)情况下提供满足条件的电磁力。此外,多线程的电磁振动幅值是单线程幅值的3倍,与理论分析结果一致。假如多线程导电选择两个线程通电,则相应振幅值约等于单线程的两倍。
4 实验及结果分析
为了验证电磁振动理论推导的合理性与电磁力分布仿真结果的正确性,现采用必能信超声(上海)有限公司提供的M836H机型搭建实验测试平台。首先在升降台上装好塑性模具,然后夹紧模具,设定系统基本参数,确认无误后,上电按下机器启动按钮,选择手动模式,关闭机器前门,使实验测试平台M836H在一定频率下振动,按照位移传感器反馈的部分数据绘制相应曲线。
电磁力分布与理论值相差1.5%属于可接受范围,基本与仿真结果一致。在单线程和多线程导电输入情况下,电磁力波峰分别大约为400N、556.080 0N,从而验证了本文理论推导的合理性及仿真结果的正确性,为设置振动摩擦焊接的外激振力大小提供了参考。
5 结语
本文提出一种基于MATLAB的电磁振动仿真分析方法,并利用振动摩擦焊接试验台对建立的电磁力理论推导方法进行实验验证。结果表明,利用电磁振动学和牛顿运动学方法建立的电磁力理论是合理的,可为以后的研究提供重要参考依据。
在下一阶段将对动态进程模式下的电磁力进行研究,由于本次实验中采集的数据点较少,因此在今后的研究中可能需要采集更多数据,以减少实验误差,得到更准确的电磁振动外激振力数值。
参考文献:
[1] 崔菊兰. 浅谈振动焊接技术在冶金设备维修中的应用[J]. 山东工业技术,2016(8):61.
[2] 余家敏,吴建民,严昊,等. 基于Matlab的电磁振动系统建模与仿真分析[J]. 机电工程,2019,36(10):1055-1059,1064.
[3] 刘勇,国伟,张涛,等. 双层电枢结构设计及其电磁力和电流密度分布[J/OL]. 弹箭与制导学报:1-6[2020-03-13]. http://kns.cnki.net/kcms/detail/61.1234.TJ.20200114.1312.002.html.
[4] 王玉彬,马祎楠. 高温超导磁通切换电机励磁线圈电磁力计算[J/OL]. 电机与控制学报:1-8[2020-03-13]. http://kns.cnki.net/kcms/detail/23.1408.TM.20191220.1437.004.html.
[5] 邓清鹏,卢彬,王涛,等. 基于电磁力近似算法的驱动电机NVH快速仿真方法[J]. 应用声学,2019,38(6):932-938.
[6] 栾世奕,王旭平. 双推杆电磁铁电磁力仿真[J]. 机床与液压,2018,46(23):139-142.
[7] RABI J, BALUSAMY T, JAWAHAR R R. Analysis of vibration signal responses on pre induced tunnel defects in friction stir welding using wavelet transform and empirical mode decomposition[J]. Defence Technology,2019.
[8] HUR Y C, KIM D , KIM B M, et al. Measurement of weld zone properties of laser-welded tailor-welded blanks and its application to deep drawing[J]. International Journal of Automotive Technology, 2020, 21(3):615-622.
[9] 王斌. 疊片铁心的电磁振动分析与实验研究[D]. 天津:天津工业大学,2018.
[10] RUITING T,GENG L. Vibration induced reciprocating sliding contacts between nanoscale multi-asperity tips and a textured surface[J]. Microgravity Science and Technology,2020,32(1): 79–88.
[11] 卢忠,胡睿,赵英鹏,等. 电磁场能量传输特性实验装置研究[J]. 浙江工业大学学报,2020,48(1):63-67.
[12] 王锦佳. 从宏观和微观两个角度看电磁力及做功问题[J]. 科技展望,2016,26(34):248-249.
[13] 李保来. 基于二维电磁场仿真电机轴向力的计算方法[J]. 微电机,2019,52(8):28-33.
[14] 黎镇浩. 基于电磁力驱动的筒形件冲压成形的数值模拟和实验研究[D]. 武汉:华中科技大学,2019.
[15] 张庆宇,涂群章,周建波,等. 永磁同步电机气隙磁场定向控制仿真分析[J]. 兵器装备工程学报,2019,40(12):105-109.
(责任编辑:黄 健)
