反应材料冲击压缩行为的三维细观数值模拟

2020-12-01杨相礼王传婷田伟玺

高压物理学报 2020年6期

杨相礼，何勇，何源，王传婷，徐涛，田伟玺，周杰

（1. 南京理工大学智能弹药技术国防重点实验室，江苏南京 210094；2. 湖北航天飞行器研究所，湖北武汉 430035）

反应材料(Reactive materials)又称活性材料、多功能含能结构材料，是一种由两种或两种以上的材料制备而成的复合材料。由反应材料制成的活性毁伤元在对目标进行毁伤的过程中，材料因受到冲击而释放出大量的化学能并引发燃烧、爆炸等附加毁伤效应[1-2]，对目标进行多重毁伤。由于其巨大的军事应用前景，以铝/聚四氟乙烯(Al/PTFE)、铝/镍(Al/Ni)为代表的反应材料近年来受到广泛的重视。

早期关于反应材料的研究主要集中在制备工艺及其反应行为和毁伤效应上，徐松林等[3-4]、赵鹏铎等[5]对Al/PTFE 反应材料的制备工艺、力学性能等进行了研究。周杰等[1,6]研究了Al/W/PTFE 反应材料组分配比与颗粒粒径对反应材料准静态压缩性能与冲击释能特性的影响。Xiong 等[7-8]使用准密闭容器研究了PTFE、Cu 等添加剂对Al/Ni 反应材料冲击释能行为的影响。

随着研究的深入，越来越多的研究表明反应材料在细观尺度上的响应行为对材料的冲击释能行为有重要的影响，而现有的理论及试验手段在揭示细观响应行为上具有一定的局限性。鉴于此，一些学者将多尺度方法应用到反应材料的研究中，例如：Eakins 等[9]、Aydelotte 等[10]采用二维数值方法对不同疏松度及颗粒形态的Al/Ni 材料的冲击响应行为进行了深入的研究；Qiao 等[11]采用随机投放方法建立了Al/W/PTFE 反应材料的细观有限元模型；Ge 等[12]基于材料的真实细观特性统计规律，建立了Al/PTFE反应材料的细观力学模型。然而上述研究结果均基于二维数值模型，或将材料颗粒假设为球形的三维模型，与材料的实际结构相差较大。

针对以上现状，采用基于真实图像的三维细观有限元模型研究Al/PTFE 与Al/Ni 反应材料的冲击压缩细观响应行为。采用球磨混合和静压的方法，制备两种反应材料试件，并使用纳米CT 设备获得材料的三维细观图像，采用图像处理技术和网格映射方法，建立基于真实图像的三维细观有限元模型，研究Al/PTFE 与Al/Ni 反应材料的细观冲击响应行为；同时依据三项式物态方程计算结果和数值模拟结果，分析两种反应材料的细观冲击温度场。本结果可为研究Al/PTFE 与Al/Ni 反应材料的冲击反应行为提供参考。

1 材料制备与细观图像获取

1.1 材料制备

本研究考虑建立零氧平衡的Al/PTFE(质量比为26.5/73.5)与等体积比的Al/Ni 反应材料的真实细观数值模型，所使用的原材料颗粒参数见表1。反应材料的制备过程参考现有的成熟工艺[6]，主要的制备过程包括原料混合、模压成型等，Al/PTFE 反应材料的制备工艺还包括真空烧结流程。材料混合采用行星球磨机完成，以40 r/min 的转速充分混合1 h，成型压力70 MPa。本研究不考虑材料的空隙，因而采用较大的压力以达到较高的密实度，Al/PTFE 材料的烧结温度为380 ℃，Al/PTFE 的烧结曲线及最终获得的Al/PTFE 反应材料试件如图1 所示。

表1 研究所用原材料及规格Table 1 Details of the materials used in this research

图1 Al/Ni 反应材料试件及Al/PTFE 烧结曲线[6]Fig. 1 Sample of Al/Ni reactive materials and the sintering profile of Al/PTFE reactive materials[6]

1.2 细观图像获取

为了获得各材料的细观图像，采用高精度纳米CT 分别对材料试样进行三维扫描，考虑到设备分辨率和射线穿透能力，需先将材料试件研磨至尺寸近似为2 mm × 2 mm × 5 mm 的长方体。测试所用的CT 设备型号为蔡司Xradia510，如图2(a)所示，扫描获得的系列细观图像的像素尺寸为2 μm，两种材料的典型细观图像如图2(b)、图2(c)所示，图中圆形区域直径约1.5 mm。在测试过程中，设备的探测器绕材料试件旋转，出于图像精度的考虑，仅重建了材料试件轴心一定半径内的细观图像。图像中较亮的部分对应材料中密度较大的组分。由细观图像可知：由于压制压力较大，PTFE 与Al 颗粒分别在两种混合材料中变形成为材料基体；Al/PTFE 材料中的Al 颗粒分布较为分散，而Al/Ni 材料中Ni 颗粒出现了较明显的堆积现象，这可能与Ni 颗粒在材料中的体积分数较高有关。

图2 本研究中使用的纳米CT 测试系统及获得的Al/Ni 与Al/PTFE 反应材料的典型细观图像Fig. 2 Nano-CT system used in this research and the obtained mesoscopic images of Al/Ni and Al/PTFE reactive materials

2 数值模型

2.1 图像处理与网格划分

从获得的细观图像中选取尺寸为0.4 mm×0.4 mm×0.4 mm 的区域(ROI)[13]。采用最佳阈值方法[14-15](Otsu method)对数字图像进行阈值分割处理，灰度高于阈值的部分认为是密度较高的金属颗粒，其余则为密度较低的材料基体。本研究中制备的反应材料具有较高的密实度（＞ 99%），故忽略细观图像中出现的少量空隙。对细观图像进行阈值分割前，需要进行图像平滑、降噪等增强措施，阈值分割后对图像进行开、闭运算等操作以填补空洞和光滑边界。最后采用网格映射算法将材料属性分配到有限元网格，考虑到计算效率，模型的网格尺寸确定为4 μm。

2.2 有限元模型

通过2.1 节的图像处理及网格映射算法，分别建立了Al/PTFE 和Al/Ni 反应材料的三维细观数值模型，将细观有限元模型导入前处理软件，在模型的上部添加一定厚度的网格，以填充飞片材料，对不同的单元集合赋予不同的材料属性。将处理后的模型导入有限元软件，赋予初始条件和边界条件，为了获得反应材料的冲击Hugoniot 关系，在模型中沿冲击方向选择有一定间距的两层单元（每层单元数10 000），以每层单元的压力p与粒子速度up的平均值作为数据结果。所建立的有限元模型如图3 所示。模型中材料的强度方程均采用Johnson-Cook 强度模型[16]，状态方程采用Mie-Grüneisen 状态方程[17]，材料参数见表2 和表3，其中：A、B、C、m、n为Johnson-Cook 模型参数，Tm为熔点， ρ0为密度，C0、S、Γ0为Mie-Grüneisen 方程参数，αv为体热膨胀系数，ΘD为德拜温度。飞片赋予Al 的材料模型。

图3 Al/PTFE 与Al/Ni 反应材料细观有限元模型Fig. 3 Mesoscopic FE models of Al/PTFE and Al/Ni

表2 Johnson-Cook 本构模型相关参数[16, 18]Table 2 Parameters of Johnson-Cook model of materials[16, 18]

表3 Mie-Grüneisen 状态方程相关参数[19]Table 3 Parameters of the Mie-Grüneisen equation of state[19]

2.3 算法及边界条件

反应材料在冲击压缩过程中，伴随着冲击波的传播，材料颗粒间发生剧烈碰撞等相互作用，引起颗粒剧烈变形、塑性流动等现象。本研究采用多物质Euler 算法来模拟反应材料的冲击压缩行为。在Euler 算法中，网格节点在计算过程中保持空间位置不变，而材料的状态参数则随材料的流动在网格节点间传递，因此适合描述高速撞击情况下材料的大变形行为。多物质Euler 算法允许单元内存在多种材料，单元的计算结果根据各材料的体积分数进行平均处理。

受模型尺寸的限制，所模拟的物理时间极短（冲击波掠过模型时间为0.06～0.16 μs），且主要研究材料的冲击加载情况，不考虑材料的冲击卸载阶段。为了在材料中产生持续稳定的平面正冲击波，设铝飞片沿z轴方向以恒定速度撞击反应材料。顶部设置流入边界，以消除自由界面的反射波，模拟半无限飞片撞击；与z轴平行的4 个侧面设置垂直于侧面方向的速度为零，以消除侧面边界产生的稀疏波；底部设置非反射边界，以消除自由界面的反射卸载。

3 结果与讨论

3.1 冲击Hugoniot 关系

为了研究不同冲击压力条件下材料的冲击响应行为，设置飞片的速度范围为250～2 000 m/s，分别采用所建立的数值模型对Al/PTFE 及Al/Ni 反应材料进行冲击压缩数值模拟研究。由于反应材料在细观尺寸上的异质性，在冲击压缩的某一瞬间，材料内部的压力处于不均匀状态，为了获得冲击Hugoniot 模拟结果，将每层10 000 个单元计算结果的平均值作为该截面上的冲击Hugoniot 结果。而冲击压力p与粒子速度up则可分别由两组压力曲线与粒子速度曲线峰值的平均值得到，由此可获得反应材料的p-up关系。根据数值模型计算获得的各材料的p-up关系如图4、图5 所示，图中曲线为根据三项式物态方程和混合物叠加准则计算出的理论结果[20]，表3 中给出了计算中需要的材料参数。由图4、图5 可知，在本研究范围内，数值模拟结果与理论计算结果一致，其中Al/PTFE 反应材料的理论和数值模拟结果与试验结果[21]吻合较好。上述结果表明，建立的反应材料细观数值模型能准确地模拟材料的宏观冲击响应行为。

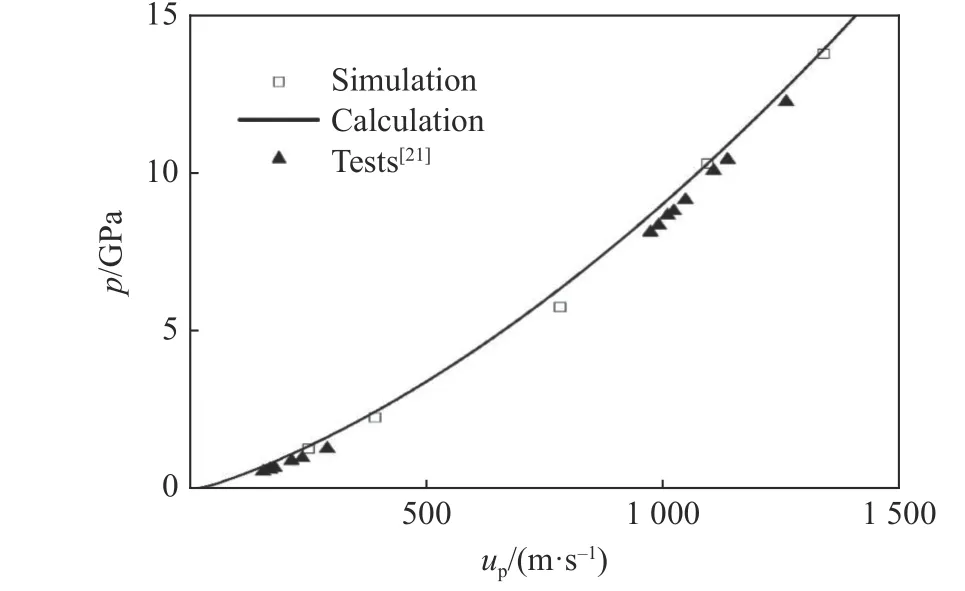
图4 Al/PTFE 反应材料的p-up 关系Fig. 4 p-up relationship of Al/PTFE reactive materials

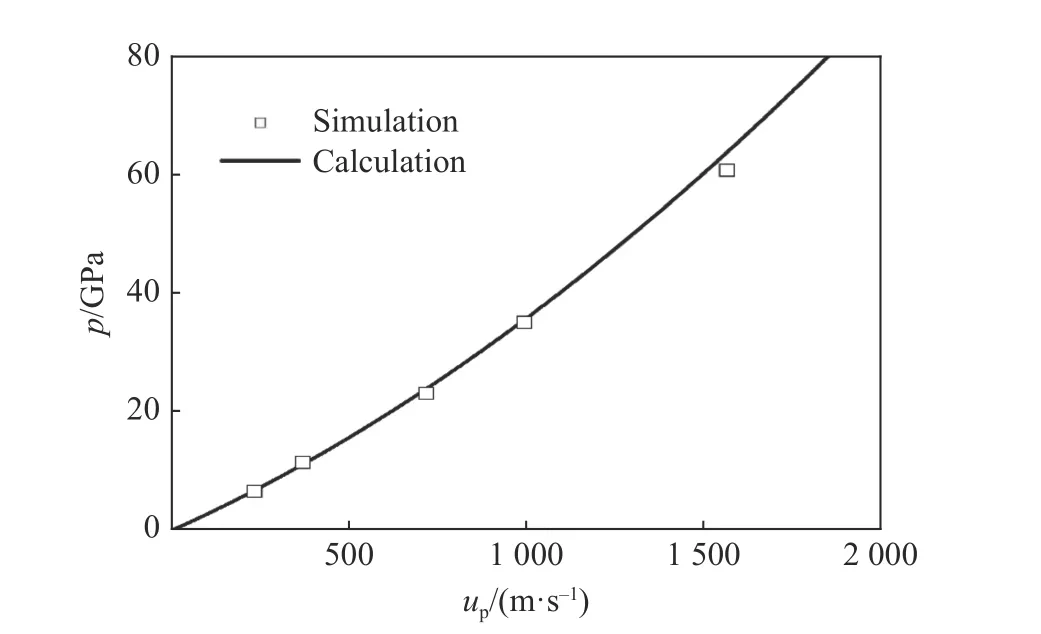
图5 Al/Ni 反应材料的p-up 关系Fig. 5 p-up relationship of Al/Ni reactive materials

3.2 细观压力与颗粒变形

反应材料在冲击压缩过程中，随着冲击波在材料中的传播，从宏观角度上看，其传播行为可用一般均质材料的传播理论描述；而从细观尺度上看，由于材料的异质性，冲击波在不同材料间传播时，必然发生透射、反射、卸载等行为，使细观尺度上的压力场趋于复杂化。图6 为撞击速度为1 500 m/s 时，3 个不同时刻（t为0.02、0.04、0.06 μs）Al/PTFE 的压力分布。高速撞击下，冲击波阵面在三维空间内均呈现出不平整状态，同时，材料的压力场在波阵面掠过后并未立即达到平衡状态；数值边界条件中飞片材料的速度为恒定值，材料的撞击端不会因反射卸载而引入稀疏波，波阵面后的压力不平衡状态是由于冲击波在细观材料颗粒间的互相反射与卸载。

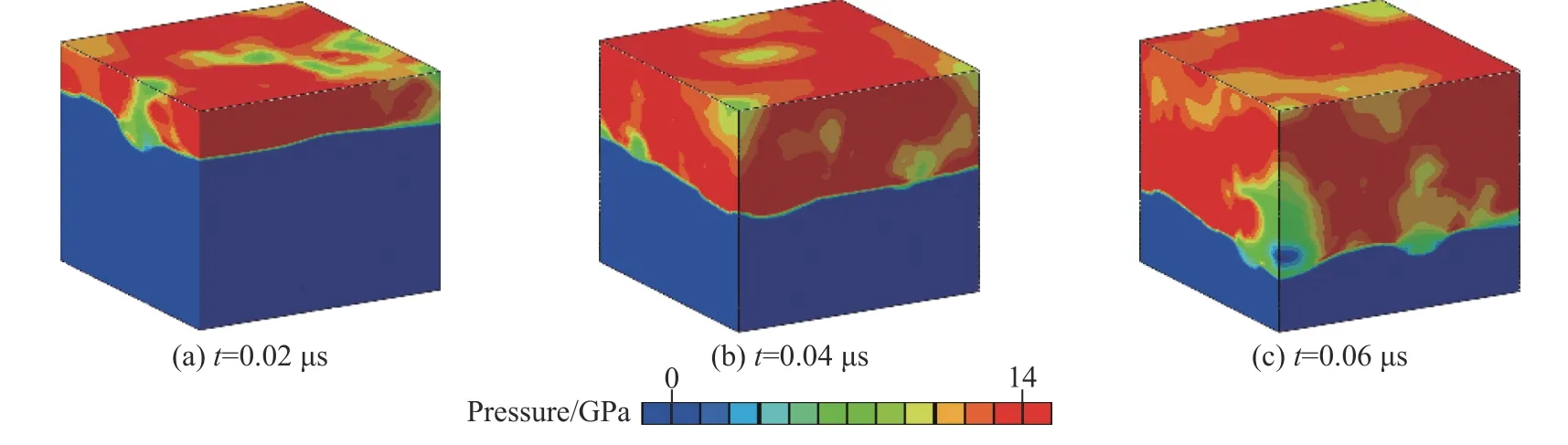
图6 撞击速度为1 500 m/s 时Al/PTFE 反应材料在不同时刻的压力分布云图Fig. 6 Pressure cloud diagrams of Al/PTFE for an impact velocity of 1 500 m/s at different times

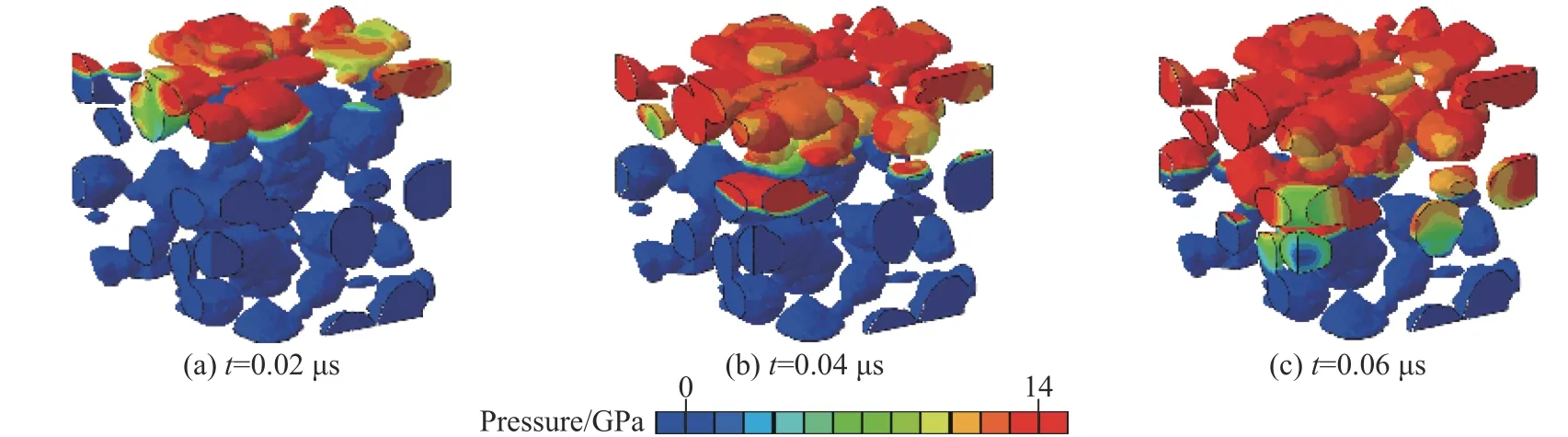
图7 撞击速度为1 500 m/s 时不同时刻Al/PTFE 反应材料中Al 颗粒的变形场Fig. 7 Deformation of Al particles in Al/PTFE for an impact velocity of 1 500 m/s at different times

图8 撞击速度分别为800、1 200、2 000 m/s 时Al/Ni 反应材料中Ni 颗粒的变形场Fig. 8 Deformation of Ni particles in Al/Ni for the impact velocities of 800，1 200 and 2 000 m/s

3.3 细观温度场

一些反应模型认为反应材料的细观冲击温升与材料的反应效率有密切的关系，反应的发生起始于冲击温升引起的质量扩散[23]。一些学者基于反应速率受控于冲击温升的假设，建立了反应材料的冲击反应理论计算模型[24-25]。在冲击波作用下，材料受到强烈的压缩作用，材料温度急剧升高，单质材料的冲击温升可由三项式物态方程计算得到[20,26-28]。又因为冲击波加载的时间尺度极短，可忽略此过程的热传递，认为材料处于绝热状态，可通过冲击压缩波后压力场及冲击温升关系获得材料的冲击温度场。

图9 为根据三项式物态方程[20]计算获得的PTFE、Al、Ni 3 种单质的冲击温升曲线，图10、图11则为根据该结果和冲击波刚好到达模型底部时的压力场获得的不同撞击速度下材料的细观温度场。与一些冲击反应理论模型中假设材料组分温度均匀有所不同，由于材料压缩性不同，两种反应材料的细观温度场呈温度较低的金属颗粒嵌在温度较高的基体材料中的状态，与一些二维模型计算结果一致[29-30]；并且，PTFE 基体与Al 金属颗粒的温差远大于Al 基体与Ni 颗粒的温差。在同等压力下，PTFE 的压缩度远大于Al、Ni 等金属材料，较大的变形吸收更多的能量，因此具有更高的温升。

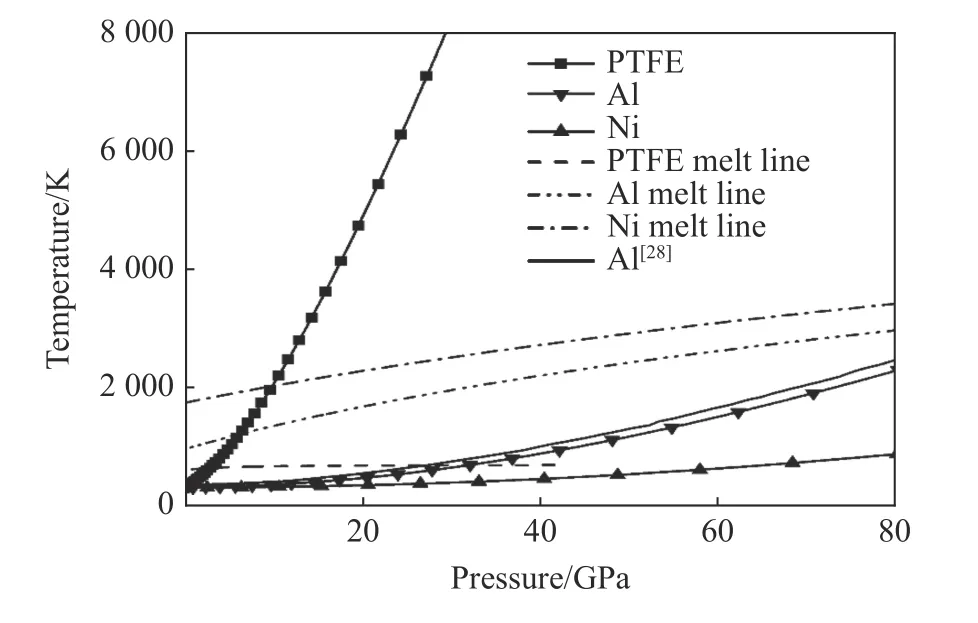
图9 材料冲击温升及高压熔点计算结果Fig. 9 Calculation results of shock temperature risesand melt lines

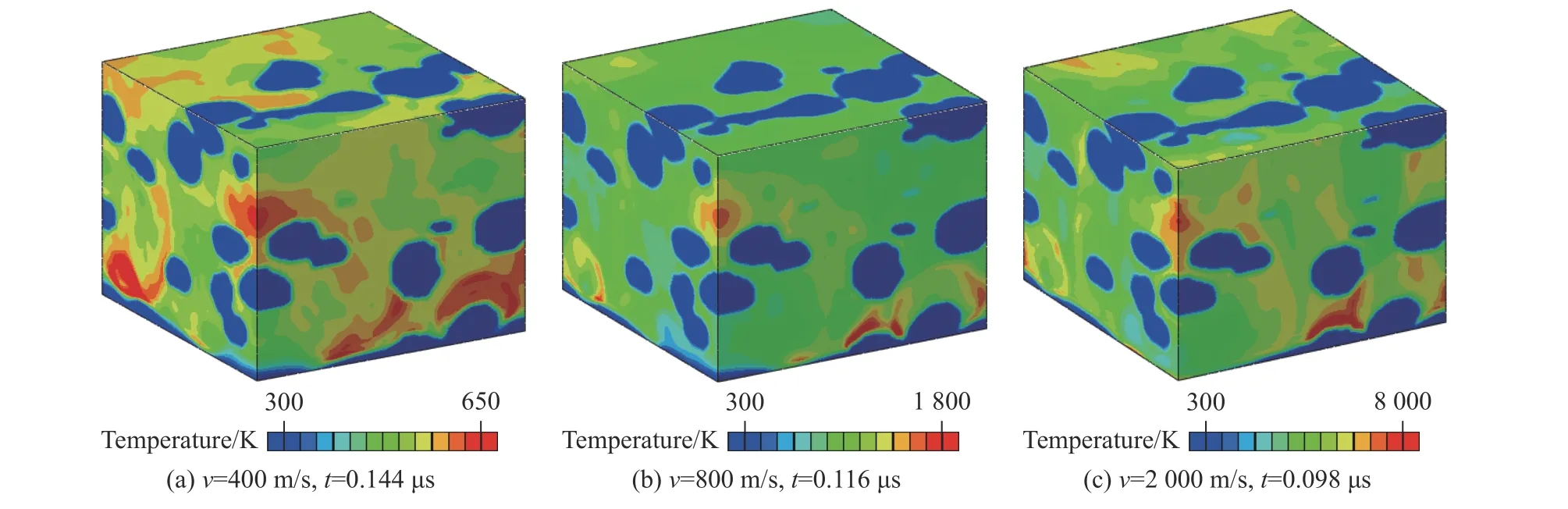
图10 撞击速度分别为400、800、2 000 m/s 时Al/PTFE 反应材料的细观温度场Fig. 10 Temperature cloud diagrams of Al/PTFE reactive materials under the impact velocities of 400, 800 and 2 000 m/s

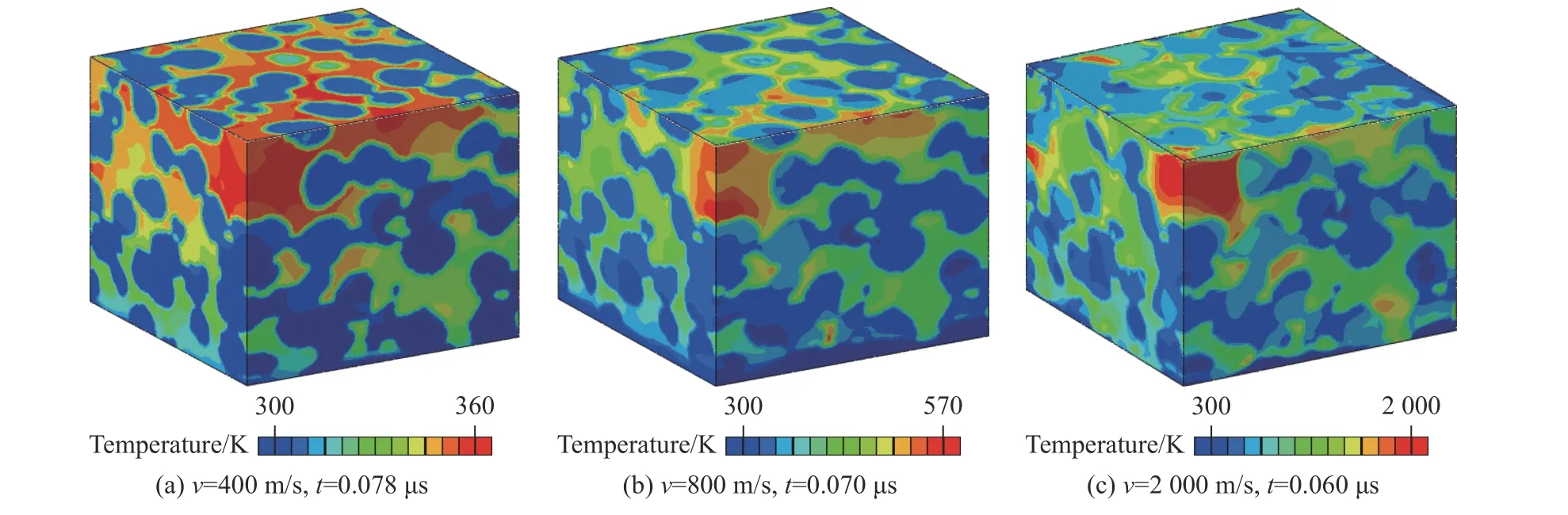
图11 撞击速度分别为400、800、2 000 m/s 时Al/Ni 反应材料的细观温度场Fig. 11 Temperature cloud diagrams of Al/Ni reactive materials under the impact velocities of 400, 800 and 2 000 m/s

图9 中高压熔点曲线与冲击温升曲线的交点即为材料的冲击熔点。由计算结果可知，PTFE 的冲击熔点极低，在冲击压力为3 GPa、温度为636 K 左右时即发生熔化。根据Al/PTFE 反应材料的温度场计算结果，当撞击速度为400 m/s 时，材料的部分PTFE 基体发生了冲击熔化；在此撞击速度下，均质PTFE 的冲击温升约为509 K，低于冲击熔点，分析认为冲击波在不同介质界面的反射使部分PTFE 基体的压力升高，达到冲击熔化温度。当撞击速度继续增大至2 000 m/s 时，PTFE 基体全部发生了熔化，作为有机高分子材料，PTFE 在较高温度下将发生热分解，释放出四氟乙烯、六氟丙烯等活性分子[32-33]。而Al 与Ni 在本研究的压力范围内保持固态。