自由曲面侧铣刀具轮廓与轨迹同步优化方法
2020-12-01王晶罗明张定华陈冰
王晶,罗明,张定华,陈冰
1.西北工业大学 航空发动机高性能制造工业和信息化部重点实验室,西安 710072 2.中国科学院 西安光学精密机械研究所,西安 710119
数控加工中,按照刀具参与切削部分的不同,可将其分为端铣和侧铣两大类。端铣是利用刀具端部切削刃切削工件的被加工曲面,由于刀具参与切削的区域较小,加工过程中误差容易控制,因此其加工效率低,但加工精度高。侧铣则是利用刀具侧刃切削工件被加工曲面,由于刀具参与切削的范围大,但刀具与曲面间的相对位置关系复杂,加工误差控制困难,因此其加工精度相对端铣要低,但加工效率更高、加工表面质量更好。一般在复杂零件精加工中常使用端铣方式,而侧铣由于上述原因,其工程应用难度较大,使用范围也仅限于直纹面、螺旋桨叶片等特定形状或特殊应用场合。在实际加工中,由于干涉等原因,对于自由曲面的凹面区域一般无法实现真正意义上的侧铣加工[1]。
近年来,为了提高加工效率和工件表面质量,国内外学者对侧铣进行了大量的研究。Wang和Yu[2]根据曲面的局部几何性质,给出了圆柱铣刀侧铣加工自由曲面的方法和加工带宽计算方法,对于凸面区域,要求刀轴方向尽量与曲面的主曲率最小绝对值对应的方向一致,以获得最大的加工带宽。曹利新等[3]提出二阶密切法,从微分几何角度研究了五轴加工中圆柱铣刀线接触自由曲面的几何原理,实现了刀具表面和被加工曲面的密切或近似密切。吴宝海和王尚锦[4]针对具有严格凸切削刃的侧铣加工刀具,提出了不发生局部干涉的充要条件是切触点处刀具曲面的正向杜邦指标线位于被加工曲面的正向杜邦指标线之内,并给出了实施干涉检查的判断准则以及消除干涉的修正方法。蔡永林等[5-7]基于鼓形刀残留高度的轨迹计算方法,实现了任意曲面叶轮叶片五轴数控加工刀具轨迹的计算。李志强和陈五一[8]建立了圆环面刀具的实际切削刃数学表达式,分析了主曲率匹配法在圆环面刀具加工中的刀具刃形误差。陈良骥和王永章[9]则研究了五轴侧铣整体叶轮的刀轴矢量确定方法,即对相邻叶片的母线进行插值,从而确定无干涉的刀轴矢量。Harik等[10]总结了包括刀具选择在内的五轴侧铣加工的研究现状。
在自由曲面侧铣加工中,由于曲面各位置上曲率不同,如果刀具选择不合适,一方面容易发生局部曲率干涉,影响曲面加工质量,另一方面也会降低加工效率。因此合理选择刀具显得非常重要。而目前在刀具轨迹规划过程中,刀具形状及尺寸均由工艺人员根据实际生产经验试选,这对工艺人员能力素质要求非常高,同时选择结果也较为保守。文献[11-14]研究了刀具尺寸的选择,然而这些研究主要集中于圆柱刀具直径的优化,对于侧铣加工中刀具形状设计的研究则较少。Chaves-Jacob等[15]提出了一种刀具形状自适应计算方法(Computation of Adapted Tool Shape, CATS)来优化直纹面侧铣加工中的刀具,继而减少给定轨迹上刀具与曲面的干涉。Li等[16]为确保曲面能够用于侧铣加工,根据鼓形刀包络面设计了相应的自由曲面,利用该鼓形刀能够实现设计曲面的高精度加工。Monies等[17]提出了一种优化直纹面侧铣加工中锥形刀具尺寸的方法,其底圆半径和锥角通过计算刀具曲面和设计曲面间的加工误差确定。Yan和Luo等[18-19]基于曲面自适应曲率匹配,结合曲面拟合技术,建立了整体叶盘侧铣加工鼓形刀轮廓设计优化算法。上述算法仅能用于标准形状刀具的尺寸优化,不能用于非标准刀具的设计。Li等[20]提出了一种用于整体叶盘五轴加工中新的鼓球铣刀(Barrel-Ball Milling, BBM),该刀具可以看作底面为球状的鼓锥形刀具。BBM刀具的尺寸可以通过自由曲面最大主曲率的最大值确定,这与文献[7]中的选择原理类似。Zheng等[21]将传统旋转刀具近似为一组球体,继而提出了一种新的无干涉的刀具尺寸优化方法。与此类似,Zhu等[22]为降低加工误差,利用球扫掠刀具回转面,并结合基于距离的刀具轨迹优化函数,实现了五轴数控加工中刀具形状和轨迹的优化。然而,受刀具表达方式的限制,上述方法主要基于已知形状的刀具设计。
对于整体叶盘、整体叶轮等自由曲面类零件,其中通常包含几十个形状相同的叶片,而设计一种专用刀具能够有效提高加工质量和效率。但目前刀具设计方面的研究主要集中于给定形状下刀具参数的优化,对于未知刀具形状下的侧铣加工轨迹规划问题的研究还较少。在国外,普惠公司[23-24]开发了ASFM/S系统,实现了针对自由曲面叶片的侧铣加工叶片曲面重构、成型刀具设计以及对应的轨迹生成,目前已成功用于50种零件的加工中,其中包含39种发动机零件。然而,由于该系统在刀具设计和轨迹规划中并没有充分考虑刀轴的影响,这可能造成侧铣加工过程中相邻刀轴的突变,从而导致刀具破损、表面质量下降等问题的发生。而在国内,目前该方面的研究还较少,因此迫切需要针对以上问题,给出一种刀具轮廓设计与侧铣轨迹规划方法。
本文以自由曲面四轴侧铣加工为对象,开展刀具轮廓与加工轨迹同步优化方法的研究。首先,通过给出刀具形状和加工轨迹的表达形式,分别建立了加工误差优化模型和刀轴光顺性优化模型,并在此基础上构建了刀具轮廓与加工轨迹同步优化模型;其次,为计算同步优化模型初值,分别给出了初始刀位和刀具轮廓计算方法,并结合序列逼近法,实现了同步优化模型的求解,获得了最优刀具轮廓及对应的侧铣加工轨迹;最后,以自由曲面为对象,验证了该同步优化方法在自由曲面侧铣加工刀具轮廓设计及加工轨迹规划中的有效性。
1 刀具轮廓与加工轨迹同步优化建模
对于自由曲面的侧铣加工中主要存在的问题有两点:一是刀具与工件间的干涉问题;二是刀轴光顺问题。其中干涉问题主要为了在保证加工精度的前提下,防止刀具与工件间发生过切或欠切现象。而刀轴光顺问题则是为了防止相邻刀轴间角度变化过大,而导致瞬时加速度或切削力增大,继而影响切削表面质量甚至引发断刀风险。为解决上述加工中存在的问题,需要建立一种同时考虑加工精度和刀轴光顺性的刀具轮廓与加工轨迹同步优化模型。
1.1 运动刀具描述
为实现图1所示通用刀具形状的描述,以刀尖点Ot为原点,刀轴方向为zt轴建立刀具坐标系Ot-xtytzt,并设刀具径向参数θ∈[0, 2π),刀具轴向参数u∈[us,ue],xtOtzt平面上的刀具母线Ct(u) =[Cx(u),Cz(u)],则对应的刀具回转面St(u,θ)可表示为
St(u,θ)=[Cx(u)cosθ,Cx(u)sinθ,Cz(u)]T
(1)
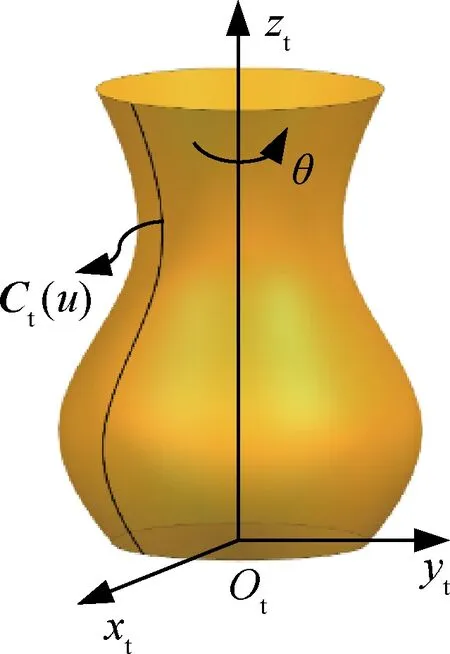
图1 通用刀具模型Fig.1 General tool model
定义刀轴轨迹面为刀具轴线沿加工轨迹线扫掠形成的曲面,由于其中包含了加工过程中刀尖点坐标及对应的刀轴矢量,因此可由其描述加工轨迹。同时,由于刀具轴线通常为直线段,故刀轴轨迹面一般为直纹面。定义刀具运动方向的参数t∈[ts,te],Qs(t)和Qe(t)分别为刀轴轨迹面上刀尖和刀根运动形成的轨迹线,则刀轴轨迹面可表示为
(2)
式中:
(3)
其中:Nj,k(t)为k次B样条基函数;Vs,j为Qs(t)上的控制顶点;Ve,j为曲线Qe(t)上的控制顶点;n+1为边界曲线上控制点数量。
则t时刻,刀轴的瞬时方向T(t)可以表示为
(4)
参考文献[25],并结合刀具回转面方程和刀轴轨迹面方程,可以得到任意形状刀具沿加工轨迹运动形成的刀具包络面,如图 2所示。
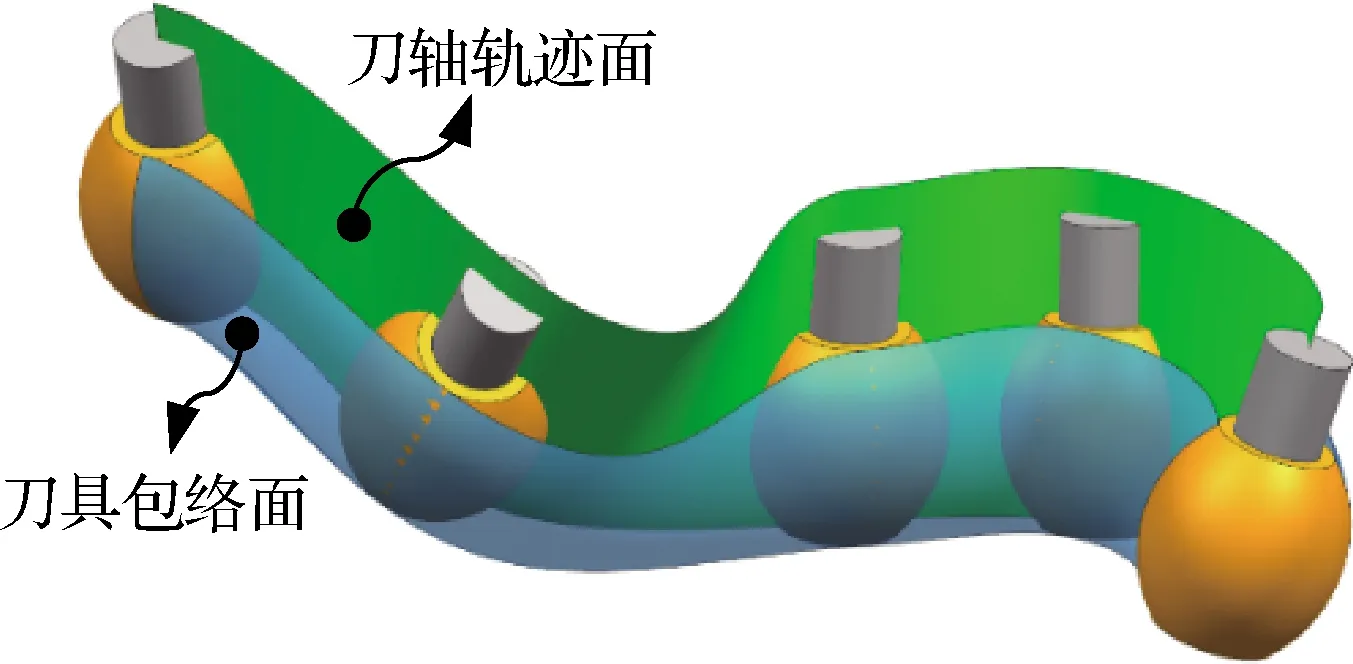
图2 刀轴轨迹面及刀具包络面Fig.2 Tool axis trajectory surface and tool envelope surface
1.2 四轴加工轨迹整体优化模型
1.2.1 基于加工误差的优化模型
对于四轴加工而言,由于刀轴始终在固定的摆刀平面Π内运动,设Π对应的法矢为nΠ,则有T(t)·nΠ=0,结合式(4)可以得到
(5)
则式(5)恒成立的充分条件是
(6)
(7)
式中:m+1为工件曲面上的采样点pi的数量;di为pi点到刀具包络面的有向最短距离;[ξ1,ξ2]为加工过程中工件允许的偏差范围。
1.2.2 基于刀轴光顺性的优化模型
为保证刀轴在加工过程中平滑过渡,应保证刀轴轨迹面Sa(u,t)尽可能光顺。曲面的几何光顺性通常可以用曲面的应变能量来表示,为简化计算,这里引入薄板能量模型E(w)[26-27]近似该曲面能量来表示轨迹面Sa(u,t)的光顺性。
(8)
将式(2)代入式(8)整理后可得
E(w)=wTMw
(9)
式中:M为6(n+1)×6(n+1)的刚度矩阵,可表示为
(10)
B为3×6(n+1)的矩阵,可表示为
B=[>B00,…,Bi 0,…,Bn0,B01,…,Bi1,…,Bn1]
(11)
式中:
(12)
加工过程中为保证刀轴整体光顺,依然可以通过调整w中的控制顶点位置,在保证加工精度的前提下,降低曲面应变能以达到光顺刀轴轨迹面,继而实现刀轴整体光顺的目的。因此,建立如下基于刀轴光顺性的侧铣轨迹优化模型:
(13)
1.2.3 加工轨迹整体优化模型
为提高加工精度、改善切削状态、提升零件表面质量,这里基于加工误差优化模型和刀轴光顺优化模型,建立侧铣加工轨迹整体优化模型:
(14)
式中:α∈[0, 1]为权系数,用于控制加工误差和刀轴光顺性在优化过程中所占的比重;D*为模型式(7)优化结果中目标函数D(w)的值;E*为模型式(13)优化结果中目标函数E(w)的值。
由于D*为模型式(7)优化结果中目标函数D(w)的值,并且两式具有相同的约束条件,因此D(w)≥D*恒成立;同理,对于E(w)≥E*也恒成立。因此,模型式(14)可简化为
(15)
1.3 刀具轮廓与加工轨迹同步优化模型
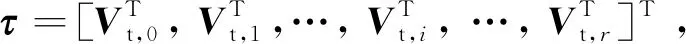
(16)
为实现刀具参数与刀轴整体光顺的同步优化,结合式(9)可知
(17)
参考模型式(13),可以建立刀具轮廓与刀轴光顺性同步优化模型
(18)
为实现同时优化侧铣加工中刀具轮廓和加工轨迹的目的,这里参考模型式(15)建立同步优化模型:
(19)
由于该同步优化模型在使用过程中需要根据不同曲面形状,设计相应的刀具轮廓,并规划侧铣加工轨迹。因此,在考虑生产周期和成本等因素的情况下,本文提出的方法主要适用于加工具有大量相同或类似结构的零件中,如整体叶盘或整体叶轮等。这类零件中通常包含几十张形状相同的叶片曲面,并且由于材料难加工,故其加工周期通常较长,且刀具需求量大,加工成本高。
2 同步优化模型求解
2.1 模型求解策略
对于刀具轮廓与加工轨迹同步优化模型式(19)而言,由于其目标函数中包含刀具包络面与工件曲面间干涉量d(x),一般情况下其很难用简单的数学表达来描述,因此不能直接采用传统的线性规划法(图形法、单纯形法等)、非线性规划法(黄金分割法、最速下降法、Newton法、Powell法、Lagrange乘子法和序列无约束极小化法等)或二次规划法(罚函数法、Wolfe算法和Lemke算法等)来求解,为此这里基于序列逼近法(Successive Approximation Method, SAM)给出其具体求解过程。序列逼近法的基本思路是在当前解处将目标函数和约束条件Taylor展开,并构造已有数学规划问题,通过对新问题的求解,并进行反复迭代直至算法收敛,继而得到原问题的最优解。其具体步骤为
1) 初始解为x(0),计算原始目标函数值F(x(0)),并令i=0。
2) 将目标函数和约束条件在x(i)处二阶Taylor展开,并构造新的关于Δx的优化问题,则原问题转化为典型的二次规划问题。
3) 利用二次规划法求解新的优化问题,得到相应的最优解Δx*。
4) 取x(i+1)=x(i)+Δx*,并计算x(i+1)处原始目标函数值F(x(i+1))。
5) 判断计算结果是否满足终止条件,当满足时,令最优解x*=x(i+1),并结束计算;否则,令i=i+1,并返回2)。
因此,为求解刀具轮廓与加工轨迹同步优化模型,需要分别将模型式(16)、式(18)和式(19)转化为典型二次规划问题。令x(s)为第s次序列逼近得到的最优解,将d(x)在x(s)处一阶Taylor展开,有
O((x(s))2)
(20)
则考虑微分扰动x(s)+Δx下,模型式(16)的非线性问题转化为线性最小二乘问题:
(21)
式中:Δxj=[Δx3j, Δx3j+1, Δx3j+2]。
定义x=x(s)+Δx,并令
(22)
在考虑微分扰动x(s)+Δx下,模型式(18)的非线性问题转化为二次规划问题
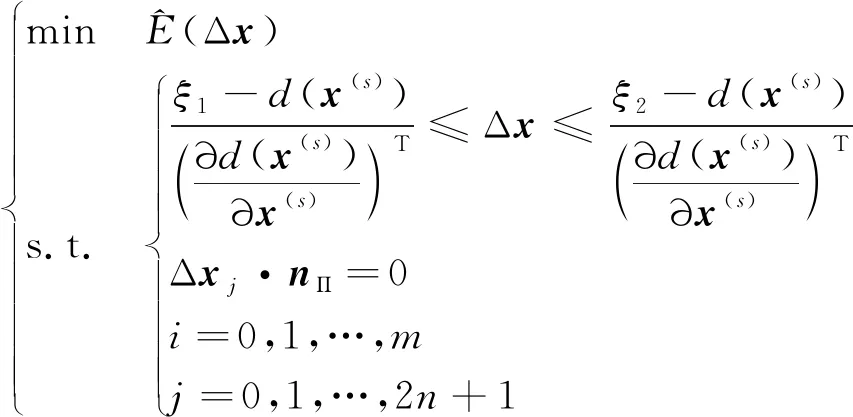
(23)
同理,在考虑微分扰动x(s)+Δx下,将式(21) 和式(23)代入式(19),则对应的刀具轮廓与加工轨迹同步优化问题转化为二次规划问题:
(24)
2.2 初始刀轴轨迹面控制参数计算
为减少优化问题求解过程的迭代步数,应尽可能保证初始刀轴轨迹面控制参数w0与最优值近似,故这里给出基于两点偏置的初始刀轴轨迹面计算方法。如图3所示,设工件曲面Sp(u,v)的参数u×v∈[us,ue]×[vs,ve]。
令边界线Cs上第j个点Ps,j=Sp(uj,vs),边界线Ce上第j个点Pe,j=Sp(uj,ve),点Ps,j在曲面Sp上的法矢为ns,j,点Pe,j在曲面Sp上的法矢为ne,j,刀具平均半径期望值为R0,采样点数量为a+1,则有
(25)

图3 初始刀轴轨迹面控制参数计算Fig.3 Calculation of control parameters on initial tool axis trajectory surface
对于四轴加工而言,为将初始刀轴约束在摆刀平面Π内,令
(26)
则Q′s,jQ′e,j为当前位置上对应的初始刀轴矢量。为计算初始刀轴矢量对应参数w0,利用两端具有重节点的k次B样条曲线拟合点集{Q′s,0,Q′s,1,…,Q′s,j, …,Q′s,a}和{Q′e,0,Q′e,1,…,Q′e,j, …,Q′e,a},令拟合后的控制点为{Vs,0,Vs,1,…,Vs,i, …,Vs,n}和{Ve,0,Ve,1,…,Ve,i, …,Ve,n},为保证点Q′s,j和Q′e,j在各自拟合曲线上有相同参数,可按照式(27)和式(28)配置样条节点向量。
利用弦长参数化法分别对两组拟合点进行参数化处理,即
(27)
为保证拟合曲线上参数一致性,结合统一平均技术给出如下节点配置公式[28]
ui=
(28)
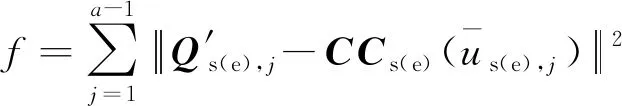
2.3 初始刀具轮廓参数计算
将图3中的直线Qs,jQe,j按照等间距离散,得到离散点qj,i,则有
(29)
如图4所示,以Qs,jQe,j为法矢构造平面ΠQs,jQe,j,并计算平面ΠQs,jQe,j上离散点qj,i到工件曲面的最近距离点pj,i,则其满足
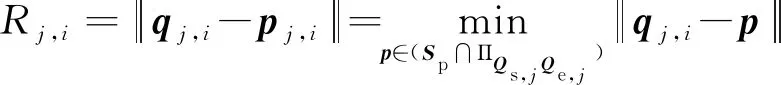
(30)
上述计算过程中当没有得到点qj,i上的Rj,i时,从点集{pj,i|i=0, 1, …,n}中删除该点,得到新的点集{pj,l|l=0, 1, …,nj}时,则其对应的Rj,l为平面ΠQs,jQe,j上qj,l点到曲面Sp的最短距离。令
(31)
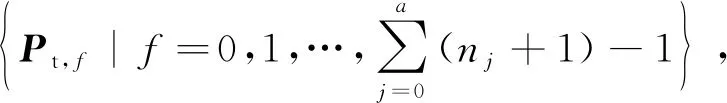
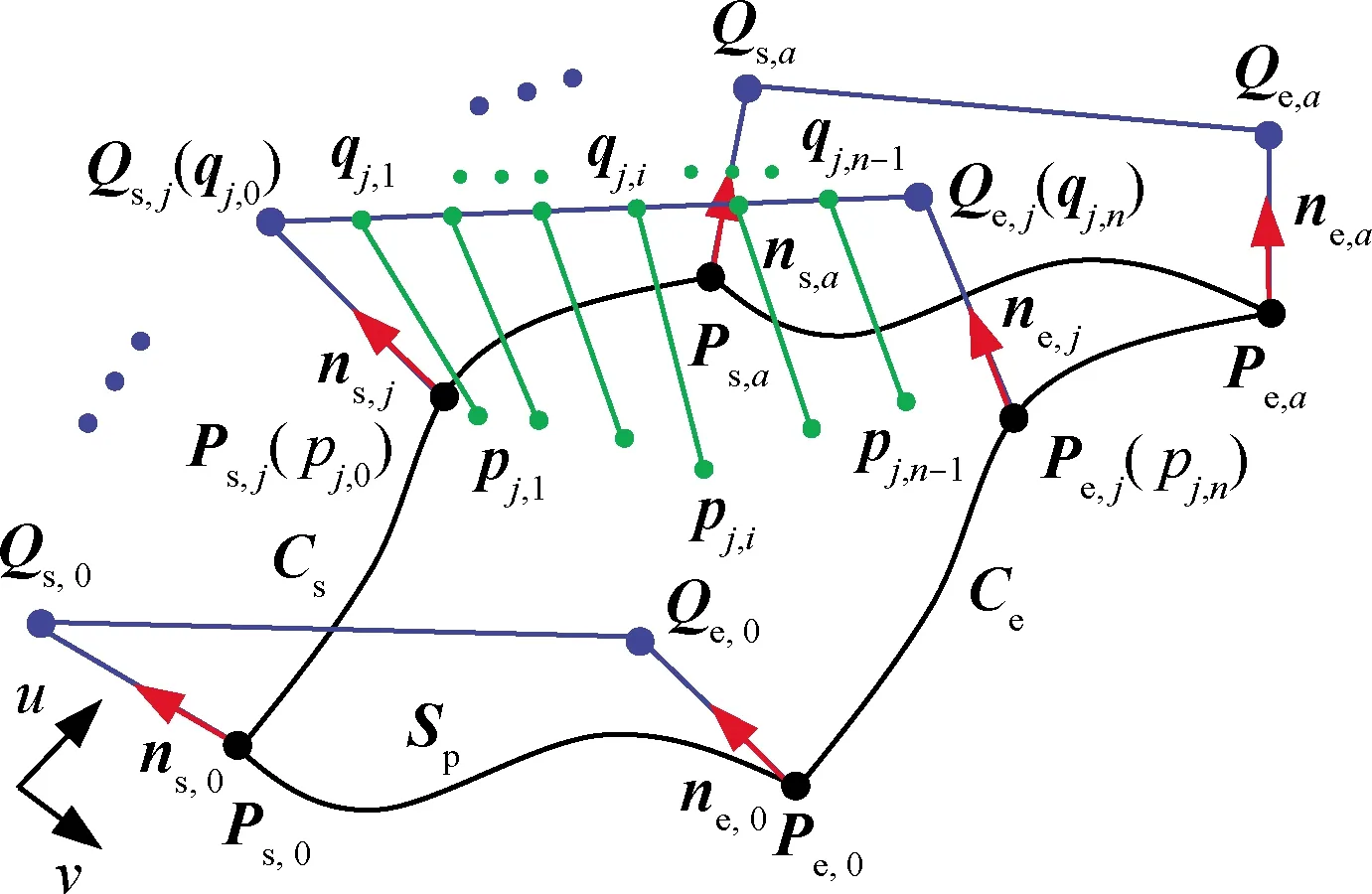
图4 刀具初始轮廓参数计算Fig.4 Calculation of parameters on initial tool contour
(32)
参考初始刀轴轨迹面控制参数计算方法,在不需要保证点集{Pt,f}与得到拟合曲线控制点集首尾点重合的前提下,进行最小二乘拟合,得到控制顶点{Vt,i|i=0,1,…,r},并由此确定初始刀具轮廓参数τ0,结合前面确定的初始刀轴轨迹面控制参数w0,即可获得同步优化模型的初值x0。
3 实验验证
为验证本文算法在刀具轮廓设计与加工轨迹优化中的正确性及有效性,以图5所示试件中的自由曲面S为对象,分别进行指定刀具下的侧铣加工轨迹规划实验,以及未知刀具形状下的刀具轮廓设计实验。

图5 自由曲面试件Fig.5 Specimen with freeform surface
3.1 加工轨迹规划实验
为验证利用本文方法生成的侧铣加工轨迹正确性及有效性,针对图5所示试件中的自由曲面S,在给定图6所示椭圆形刀具的基础上规划四轴侧铣加工轨迹,相应的刀具参数如表1所示。
按照2.1节中给出的初始刀轴轨迹面控制参数计算方法,得到刀轴轨迹面控制顶点如表2所示,相应的刀轴轨迹面及刀具位姿如图7所示,可以看出这时刀具与工件间的偏差较大。
令侧铣加工过程允许的偏差范围为[-0.02, 0.20] mm,利用1.2节中给出的基于加工误差的轨迹优化模型式(7),计算相应的侧铣加工轨迹并进行分析,能够得到曲面S上的误差分布如图8(a)所示,则工件上的加工误差控制在[-0.02, 0.06] mm范围内,相应的平均误差为0.005 mm,均方差为0.011 mm。利用基于刀轴光顺性的轨迹优化模型式(13)计算相应的侧铣加工轨迹,能够得到曲面S上的误差分布如图8(b)所示,则相应的加工误差为[-0.02, 0.14] mm,平均误差0.020 mm,均方差0.023 mm。取加权系数α=0.8,并利用加工轨迹整体优化模型式(15)计算相应的侧铣加工轨迹,能够得到曲面S上的误差分布如图8(c)所示,则相应的加工误差为[-0.01, 0.07] mm,平均误差0.011 mm,均方差0.010 mm。为方便与本文方法进行对比,这里利用UG软件生成相应的侧铣加工轨迹,可以得到曲面S上的误差分布如图8(d)所示,则相应的加工误差为[-0.05, 0.10] mm,平均误差0.023 mm,均方差0.024 mm。

图6 椭圆形刀具Fig.6 Oval form tool

表1 椭圆形刀具参数Table 1 Parameters of oval form tool
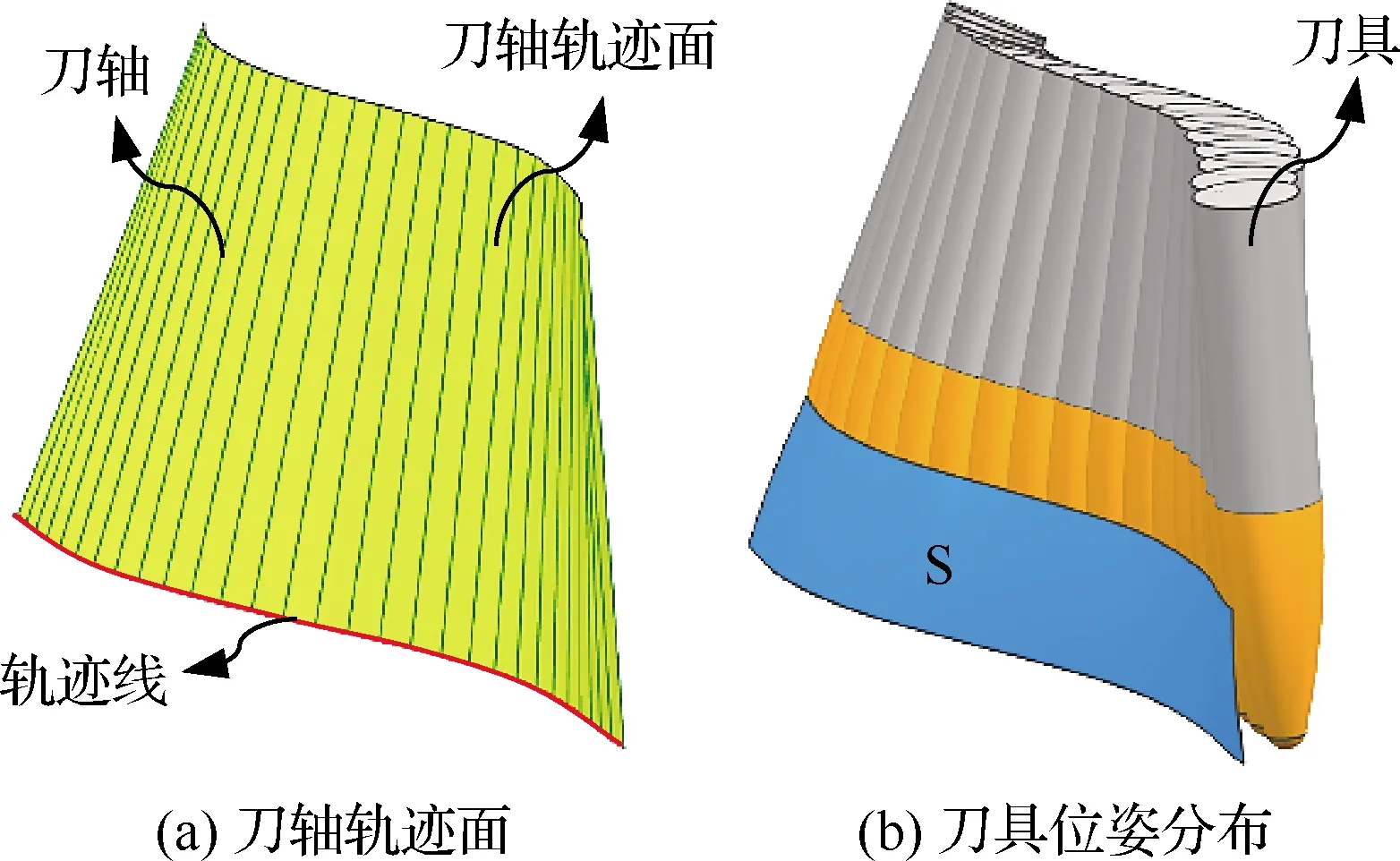
图7 初始侧铣加工轨迹Fig.7 Initial tool path of flank milling

表2 初始刀轴轨迹面控制顶点Table 2 Initial control points of tool axis trajectory surface
可以看出,采用基于加工误差的轨迹优化模型和加工轨迹整体优化模型生成的侧铣轨迹加工时,工件上的平均误差和均方差均较小,说明误差集中在平均误差附近,且整体较小。
图9所示为在XYZA结构四坐标机床上加工时,不同轨迹优化方式得到的侧铣加工轨迹下,机床A角随切削轨迹长度的变化情况。
由计算结果可以看出,采用基于刀轴光顺性的轨迹优化模型和加工轨迹整体优化模型生成的侧铣加工轨迹加工时,刀轴整体较光顺。因此,利用本文提出的轨迹整体优化模型,能够在保证刀轴光顺前提下,尽可能减小加工误差,继而提高加工精度和工件表面质量。表3所示为采用整体优化模型得到的刀轴轨迹面控制顶点,相应的侧铣加工轨迹如图10所示。
在YH850Z四坐标加工中心上,利用图6所示的椭圆刀具进行实际加工,试件材料为环氧树脂,能够得到图11所示的加工结果,可以看出切削完成后的表面较光顺。
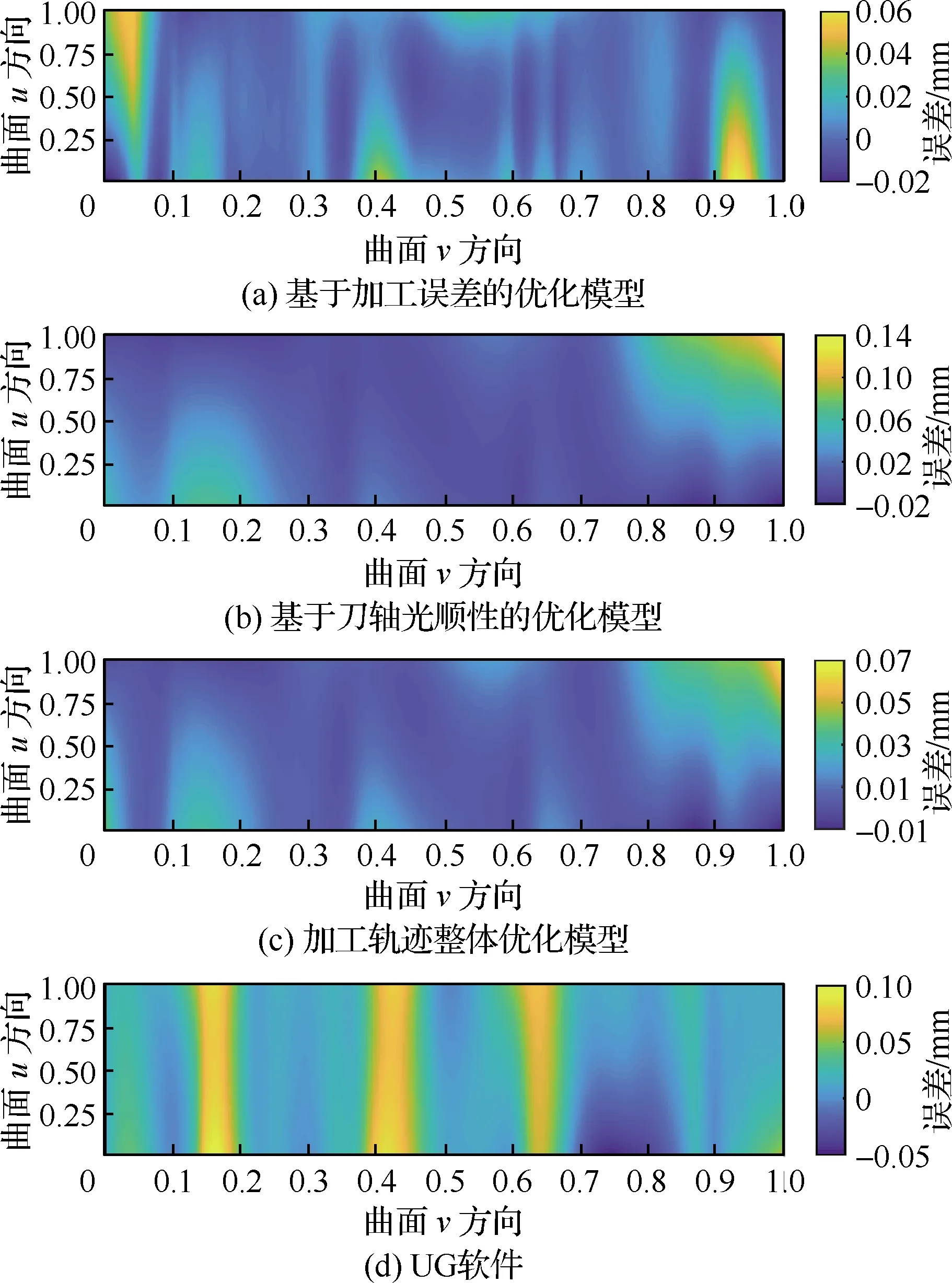
图8 不同方法下被加工曲面上的侧铣加工误差分布Fig.8 Error distribution of different flank milling on sculptured surface

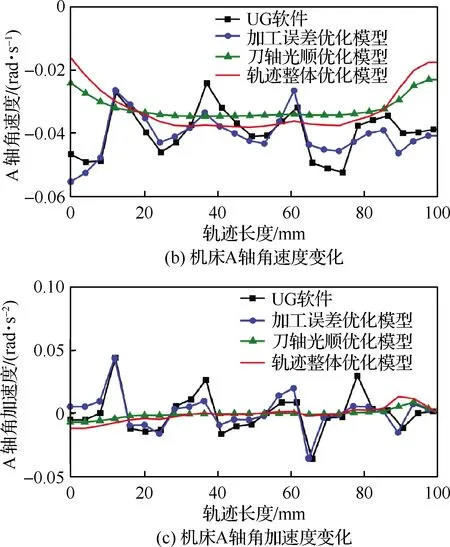
图9 不同算法下的机床转动坐标变化关系Fig.9 Rotation coordinate changes of different methods on machine tool

表3 优化后的刀轴轨迹面控制顶点
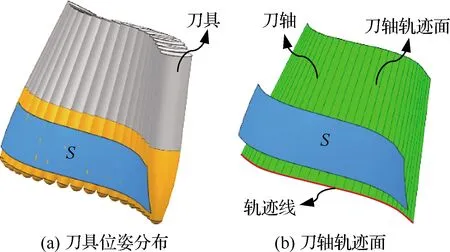
图10 优化后的侧铣加工轨迹Fig.10 Optimized toolpath of flank milling

图11 椭圆形刀具侧铣加工结果Fig.11 Flank milling results with oval form tool
3.2 刀具轮廓设计实验
为验证利用本文方法设计的刀具加工时,能够进一步提高加工质量,这里同样以图5所示试件中的自由曲面S为对象,并取刀具平均半径的期望值R0=5 mm,则根据2.3节给出的初始刀具轮廓参数计算方法可以得到图12所示刀具母线。
可以看出这时刀具切削刃长14.5 mm,为保证刀具能够最大限度的切削被加工曲面,可将刀具母线适当向两端延伸,这里令刀具母线z∈[-5, 20]mm,同时将刀具母线沿z轴向右移动5 mm,则这时初始刀具轮廓母线上的控制点坐标如表4所示。
令加工过程中工件允许的偏差范围为[-0.02, 0.20] mm,并取优化过程中的加权系数α=0.8,则根据1.3节中给出的刀具轮廓与加工轨迹的同步优化方法,可以得到表5所示的刀具轮廓母线上的控制点。
根据表5中的控制顶点构造相应的刀具轮廓母线,同时为扩展刀头部分的可加工性,在刀具端部增加球头部分,可设计图13所示的刀具。
同步优化结果中同时还会得到表6所示的刀轴轨迹面控制顶点,则相应的侧铣加工轨迹如图14 所示。
通过分析能够得到曲面S上的误差分布如图15 所示,则工件上的加工误差控制在[-0.01, 0.04] mm范围内,相应的平均误差为0.003 mm,均方差为0.007 mm。与图8(c)所示给定椭圆形刀具下轨迹整体优化模型得到的侧铣加工结果对比,可以看出其加工结果平均误差和均方差均得到了大幅下降。因此,利用同步优化模型设计的刀具和生成的轨迹进行加工,能够大幅提高加工结果精度。

图12 初始刀具轮廓母线Fig.12 Initial generatrix of tool contour

表4 初始刀具轮廓母线上的控制点Table 4 Initial control points of tool generatrix

表5 优化后刀具轮廓母线上的控制点Table 5 Optimized control points of tool generatrix
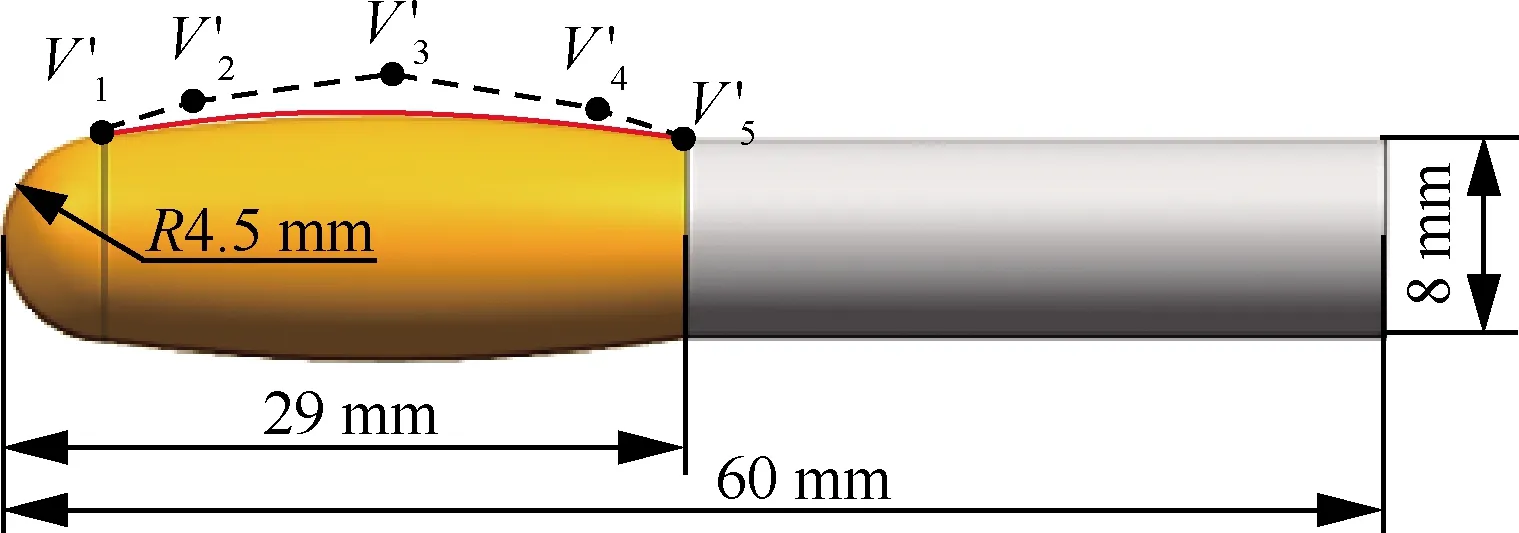
图13 同步优化下的刀具形状Fig.13 Simultaneous optimized tool contour

表6 同步优化下的刀轴轨迹面控制顶点

图14 同步优化下的侧铣加工轨迹Fig.14 Simultaneous optimized toolpath of flank milling
图16所示为在XYZA结构四坐标机床上加工时,机床A角随切削轨迹长度的变化情况。可以看出,相比于给定椭圆形刀具下轨迹整体优化模型得到的侧铣加工轨迹,刀轴变化更加光顺,这在一定程度上进一步提高了加工精度和工件表面质量。
在YH850Z四坐标加工中心上利用上述设计的刀具和生成的侧铣加工轨迹进行试件的加工,试件材料为环氧树脂,能够得到图17所示的加工结果,可以看出切削完成后的表面较光顺。
综上所述,可以看出利用本文提出的刀具轮廓与加工轨迹同步优化方法,设计的刀具形状和生成的侧铣加工轨迹加工时,能够在保证刀轴光
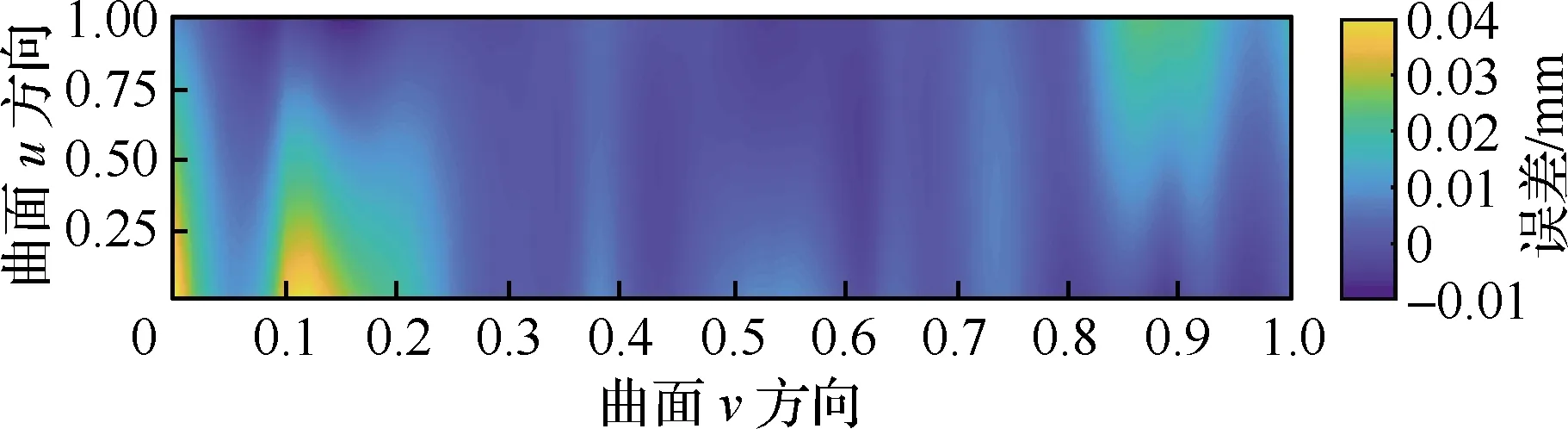
图15 同步优化下被加工曲面上的误差分布Fig.15 Error distribution of simultaneous optimization methods on sculptured surface

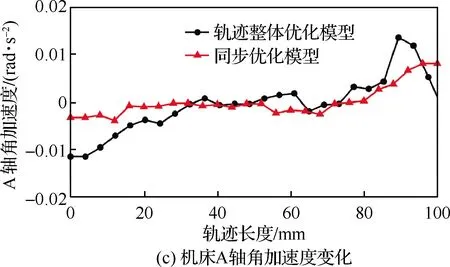
图16 同步优化下的机床转动坐标变化情况Fig.16 Rotation coordinate changes of simultaneous optimization methods on machine tool

图17 设计刀具的侧铣加工结果Fig.17 Flank milling results with designed tool
顺前提下,进一步降低试件表面上的加工误差,提高加工精度和表面质量。
4 结 论
1) 给出了刀具形状和侧铣加工轨迹的表达方法,建立了四轴侧铣加工轨迹整体优化模型,并在此基础上给出了刀具轮廓与加工轨迹同步优化方法。
2) 提出了基于序列逼近的同步优化模型求解方法,并分别给出了模型优化初值中刀轴轨迹面控制参数和刀具轮廓参数计算方法。
3) 以自由曲面试件为对象,分别通过指定刀具下的侧铣加工轨迹规划实验和未知刀具形状下的刀具轮廓设计实验,验证了本文提出的同步优化方法在自由曲面四轴侧铣加工刀具轮廓设计和加工轨迹规划中的正确性和有效性。
